Základní řadící algoritmy

Selection sort, Insertion sort, Bubble sort, Heap sort, Quick sort - popis, složitost

Řadící algoritmy slouží k řazení vstupních dat (prvků vstupního souboru) dle velikosti, je jedno zda vzestupně či sestupně. Základními operacemi jsou srovnání a přesun. Při výběru řadicího algoritmu je třeba mít na paměti několik kritérií:

Časová složitost
Implementační složitost
Vhodnost pro danou datovou strukturu
Stabilita algoritmu

Časová složitost a implementace

Nejvýkonnějšími algoritmy jsou ty, které neporovnávají jednotlivé hodnoty prvků, ale fungují na jiném principu řazení (složitost O(n)) např:

Counting sort - řazení počítáním četnosti jednotlivých hodnot
Radix sort - číslicové řazení (řadí řetězce fixní délky dle jednotlivých znaků)

Ani jeden z výše uvedených algoritmů však není vhodný pro všeobecné použití.

Algoritmy pro univerzální použití třída O(n * log(n)):

Pro malá vstupní data jsou vhodnější algoritmy s jednoduchou implementací a s kvadratickou složitostí O(n²):

Nejvýkonnější algoritmus s kvadratickou složitostí je Shell sort.

Stabilita algoritmu

Stabilní algoritmus je takový, u nějž nedojde během řazení k prohození dvou prvků se stejnou hodnotou. Jako příklad užitečnosti stability algoritmu může pýt řazení žáků v třídní knize dle jména a příjmení. Stabilní algoritmus seřadí jména Bruno Semerek a Vrundo Semerek s prvním v pořadí Bruno Semerek. Nestabilní algoritmus by při druhém řazení mohl výsledky zpětně přehodit (Vrundo Semerek, Bruno Semerek).

Přirozenost algoritmu

Přirozený algoritmus rychleji zpracuje již částečně seřazenou posloupnost dat.

Třídění na místě

Algoritmus třídí prvky na místě, pokud prvky neopouštění paměťové buňky, v nichž byly zadány. Nicméně, algoritmus může využít tzv. pracovní buňky, kam si ukládá číselné proměnné (indexy, parametry...) tato uložená data jsou pomocnou pamětí algoritmu.

Tabulka níže zachycuje jednotlivé třídící algoritmy včetně jejich složitosti a jiných vlastností. Pro účely SZZ bude poslední kapitola otázky věnována funkcionalitě každého algoritmu, u nějž je poznámka NAUČIT SE.

Srovnání třídících algoritmů

Název	CZ Název	Přirozený	Stabilní	Složitost	Poznámka
Bubble sort	Bublinkové	ANO	ANO	O(n²)	NAUČIT SE
Shakesort	-	ANO	ANO	O(n²)
Selection sort	Výběrem	NE	NE	O(n²)	NAUČIT SE
Insertion sort	Vkládáním	ANO	ANO	O(n²)	NAUČIT SE
Shell sort	Schellovo	ANO	NE	O(n²)
Heapsort	Haldou	NE	NE	O(n log(n))	NAUČIT SE
Merge sort	Slučováním	ANO	ANO	O(n log(n))
Quicksort	Rychlé	NE	NE	O(n log(n))	NAUČIT SE
Radix sort	Číslicové	NE	ANO	O(n)
Counting sort	Počítání četnosti	NE	ANO	O(n)
Bucket sort	Přihrádkové	-	ANO	O(n * k)
Comb sort	Hřebenové	ANO	NE	O(n²)

zdroje:
https://www.algoritmy.net/article/75/Porovnani-algoritmu
https://cs.wikipedia.org/wiki/%C5%98adic%C3%AD_algoritmus

Skupiny třídících algoritmů

1. Vnitřní třídění

Základní vlastností algoritmů tzv. vnitřního třídění je, že všechny tříděné prvky jsou uloženy ve vnitřní paměti počítače (Registry, RAM, Cache aj.). Výhodou vnitřního třídění je, že veškeré operace (srovnání či přesuny) probíhají pouze nad hodnotami v interní paměti.

Dle základní operace PŘESUNU dělíme algoritmy třídění do tří skupin:

Vkládáním - Insertion sort, Shell sort
Výměnou - Bubble sort, Quicksort
Výběrem - Selection sort

U třídění vkládáním zvětšujeme posloupnost tím, že vkládáme jednotlivé prvky na příslušná místa.

U třídění výměnou třídíme posloupnost záměnou dvou vybraných prvků , až dosáhneme úplného setřídění.

U třídění výběrem postupně vybíráme jednotlivé prvky ze vstupu a přidáváme je k postupně tříděné posloupnosti.

Specifickou metodou vnitřního třídění je třídění haldou, kde halda je binárním stromem. jehož prvky se de facto vyměňují.

Jednoduché metody vnitřního třídění - PŘÍMÉ

Účinější metody vnitřního třídění

2. Vnější třídění

U algoritmů s vnějším tříděním jsou tříděné prvky uloženy v externí paměti, odkud jsou po částech převáděni do paměti vnitřní, kde nad nimi proběhne daná operace. Poté jsou data opět přesunuta zpět do paměti externí. Kvůli zápisu do vnitřní paměti a zpět do vnější je tento postup pomalejší, než u vnitřního třídění. Vnější třídění je vhodné pro velké objemy dat.

Vybrané algoritmy a jejich rozbor

Selection sort - třídění výběrem

Nestabilní algoritmus se složitostí O(n²). V porovnání s dalšími kvadratickými algoritmy je tento obecně rychlejší než Bubble sort, ale pomalejší než Insertion sort. Výhodou výběrového algoritmu je jeho konstantní paměťová složitost.

De facto řadíme pole prvků tak, že vezmeme největší / nejmenší prvek řady a dáme jej na začátek. Poté vezmeme opět největší / nejmenší ze zbytku pole a dáme jej na druhé místo všech atd.

PŘÍKLAD

Pole je zprvu nesetříděné - všech n prvků je neuspořádaných
Pole je rozdělené na dvě části, setříděná a nesetříděná
1. Zapamatujeme si index prvního prvku v nesetříděné části
2. Procházíme zbytek nesetříděného pole a každý prvek porovnáváme s prvkem na první pozici
3. Je-li srovnávaný prvek menší, jeho pozice se stane pozicí s indexem 0(nahradí původně zapamatovaný prvek) - nejmenší z těchto prvků se na onen index přesune
Po každém průběžném kroku zvětšujeme setříděnou část pole o 1 prvek (posuneme hranici mezi setříděnou a nesetříděnou částí doprava)
V okamžiku, kdy setříděná část obsahuje n - 1 prvků je pole sorted, neboť v unsorted části již zbývá jen největší prvek, který je také na své konečné pozici

Mějme řadu 7 1 2 8 4 5 3 9.

zapamatujeme si pozici čísla 7
srovnáme s 1
zapamatujeme si pozici prvku 1
srovnáváme s dalšími prvky 2 8 4 5 3 9
nejmenší je 1, ergo vyměníme za 7
zapamatovaná je pozice prvku 1
řada vypadá následovně: 1 | 7 2 8 4 5 3 9
zapamatujeme si pozici prvku 7
srovnáme s 2, prvek 2 je menší, tak si zapamatujeme jeho pozici
srovnáme se zbytkem pole
2 je nejmenší, máme zapamatovanou pozici a vyměníme tedy prvek 2 za 7
pole vypadá takto: 1 2 | 7 8 4 5 3 9
zapamatujeme si index prvku 7
porovnáme se zbytkem pole
v průběhu si zapamatujeme pozice menších prvků, tj. nejprve 4
porovnáváme dále, narazíme na prvek 3, protože je menší než zapamatovaná 4 a posléze porovnávaná 9, přesuneme jej na pozici 3 (index [2])
1 2 3 | 7 8 4 5 9
atd.

Insertion sort - třídění vkládáním

Algoritmus vkládání je stabilní algoritmus založený na principu porovnávání řazených prvků. Výhodou Insertion sort je, že u téměř setříděného pole se složitostí blíží k O(n). Dochází pouze k průchodu, nikoli samotným posunům. Pro řazení malých polí (cca do 10 prvků je Insertion sort rychlejší, než Quicksort).

PŘÍKLAD

Mějme 1 prvek, ten je triviálně seřazen
Vezměme následující prvek a zařaďme jej na správné místo v jichž seřazených prvcích (seřazená část pole se zvětší o 1)
Dokud pole obsahuje nesetříděné prvky GOTO: 2

Mějme řadu 7 1 2 8 4 5 3 9.

rozdělíme na 2 části: 7 | 1 2 8 4 5 3 9
prvek 1 z nesetříděné části uložíme do proměnné x
7 | • 2 8 4 5 3 9
srovnáme prvek 7 s var x
x < 7, 7 se posune doprava
• | 7 2 8 4 5 3 9
již není co srovnávat, uložíme var x na volnou pozici a posuneme hranici setříděné části doprava
1 7 | 2 8 4 5 3 9
uložíme první prvek nesetříděné části, tj. prvek 2 do var x
tím se uvolní místo
1 7 | • 8 4 5 3 9
srovnáme x < 7, 7 se posune doprava
1 • | 7 8 4 5 3 9
dále srovnáme var x s 1, jelikož 1 < x, uložíme na aktuální pozici hodnotu var x
1 2 | 7 8 4 5 3 9
posuneme opět hranici setříděné části doprava
1 2 7 | 8 4 5 3 9
uložíme první prvek nesetříděné části, ergo 8 do var x, tím uvolníme místo
srovnáme prvek 7 s var x, 7 < x, tedy vložíme var x zpět na stejnou pozici a posuneme opět hranici
1 2 7 8 | 4 5 3 9
vezmeme prvek 4 a uložíme jej do var x
uvolníme místo
1 2 7 8 | • 5 3 9
porovnáme s prvky vlevo, dokud jsou setříděné prvky > var x, posouváme dané prvky doprava a porovnáváme dál
1 2 7 • | 8 5 3 9
1 2 • 7 | 8 5 3 9
prvek 2 < než hodnota var x, tedy uložíme na pozici [3] var x a posuneme opět hranici setříděné části doprava
1 2 3 7 8 | 5 3 9
atd.

Bubble sort - třídění výměnou

Jedná se o jednoduchý stabilní třídící algoritmus s kvadratickou asymptotickou složitostí, jehož vylepšená varianta je tzv. shakesort, což je de facto oboustranný bubblesort.

Řazené prvky jsou jako bublinky, kdy lehčí bublinka (prvek s nižším číslem) probublá na konec pole. V rámci algoritmu srovnáváme 2 sousední prvky a pokud je lehčí prvek vlevo, tak je algoritmus prohodí. Tím se prvek s menší hodnotou dostane blíže k pravému konci řady.

Se stejnou logikou pokračujeme na dalším indexu. Pokud je napravo prvek "lehčí" (má menší hodnotu), tak jej algoritmus nechá být a postoupí na další index. Každou iterací se tímto způsobem dostane na konec pole (doprava) ta nejlehčí bublinka.

Samozřejmě podmínka může být i obráceně a řadíme naopak vzestupně.

Po n-1 průchodech je pole seřazeno.

PŘÍKLAD (vzestupné řazení)

mějme řadu 7 1 2 8 4 5 3 9
postupně srovnáváme sousední prvky
7 > 1 - prohazujeme
1 7 2 8 4 5 3 9
7 > 2 - prohazujeme
1 2 7 8 4 5 3 9
7 < 8 - necháváme
1 2 7 8 4 5 3 9
8 > 4 - prohazujeme
1 2 7 4 8 5 3 9
8 > 5 - prohazujeme
1 2 7 4 5 8 3 9
8 > 3 - prohazujeme
1 2 7 4 5 3 8 9
8 < 9 - necháváme a pouštíme další průchod (řadíme již jen 7 prvků)
1 < 2 - necháváme
2 < 7 - necháváme
7 > 4 - prohazujeme
1 2 4 7 5 3 8 | 9
7 > 5 - prohazujeme
1 2 4 5 7 3 8 | 9
7 > 3 - prohazujeme
1 2 4 5 3 7 8 | 9
7 < 8 - necháváme
další průchod (řadíme již jen 6 prvků)
1 < 2 - necháváme
2 < 4 - necháváme
4 < 5 - necháváme
5 > 3 - prohazujeme
1 2 4 3 5 7 | 8 9
ostatní je okay - další průchod (řadíme již jen 5 prvků)
1 < 2 - necháváme
2 < 4 - necháváme
4 > 3 - prohazujeme
1 2 3 4 5 | 7 8 9
zbytek je okay - další průchod již není potřeba

Quicksort - rychlé třídění výměnou

Jedná se o nestabilní algoritmus s kvadratickou složitostí. Ačkoli zvolíme-li dobrého pivota (počáteční prvek), zrychlí se algoritmus na O(n * log n) očekávanou složitost. Tento algoritmus vymyslel v roce 1962 Sir Charles Hoare.

Principem algoritmu je zvolit počáteční prvek (pivot) a porovnáváme jej s každým prvkem. Menší prvky řadíme na jednu stranu od pivota a větší prvky na druhou stranu. Postup opakujeme por obě části, již bez pivota, neboť ten je umístěn na správném místě po prvním průchodu.

Pro řazení malých polí není Quicksort ideální, protože nemusí dojít k dobrému rozdělení pole na ideální poloviny. Lepší je jej použít na třídění velkého pole.

Strategie volby pivota Volba prvního či posledního prvku pole není ideální, neboť dojde k nedobrému dělení pole a nárůstu složitosti. Lepší je volit medián prvního, prostředního a posledního prvku řazeného úseku pole.

Druhou možnou strategií je výběr náhodného prvku. V praxi fungují pseudonáhodné RNG.

PŘÍKLAD - řazení vzestupně

mějme řadu 7 1 9 5 4 8 3 2
na začátku si zvolíme první prvek, naše řada má sudý počet prvků, ergo bereme prvek s nižším indexem z prvků 5 a 4
pro určení indexu daného prvku můžeme využít též vzorec: \[s = \frac{k + l}{2}\] kde \(k\) je počáteční index tříděného úseku a \(l\) je konečný index tříděného úseku
pivotem je prvek 5
nyní pracujeme s indexy i a j
i = 0, j = 7
řadíme menší ku pivotu doleva, větší ku pivotu doprava
po hledání pole
7 1 9 5 4 8 3 2
prvky vyměníme
2 1 9 5 4 8 3 7
máme nové indexy i = 1, j = 6
1 je vpravo správně, ergo posouváme index
i = 2, j = 6
2 1 9 5 4 8 3 7
3 < 9, prvky prohodíme -> 3 je menší než 5 a má být nalevo
2 1 3 5 4 8 9 7
nové indexy i = 2, j = 5
prvek 3 okay, 8 okay
nové indexy i = 3, j = 4
2 1 3 5 4 8 9 7
vyměníme, neboť 4 má být od pivota (5) nalevo
2 1 3 4 5 8 9 7
poté co se pivot posunul, se změnili indexy (i > j)
i = 4 (zleva), j = 3 (zprava) tím třídící krok končí a pole se dělí na dvě části
2 1 3 4 | 5 8 9 7
nyní každou část třídíme zvlášť (A | B)
určíme pivoty, pro A 1, pro B 8
2 1 3 4
i = 0, j = 3
kroky hledání 2 není okay, 4 je okay
i = 0, j = 2
2 není okay, 3 je okay
i = 0, j = 1
2 1 3 4
prvky vyměníme, aby vetší od pivota bylo vpravo
1 2 3 4
posuneme indexy i = 1, j = 0, (i > j) ukončí se krok a rozdělí pole
1 | 2 3 4
levá část má jeden prvek a považuje se tudíž za seřazenou
pravá část 2 3 4
pivot je 3
i = 1, j = 3 (indexace bere stále v potaz první prvek 1)
2 je okay, 4 je okay
i = 2, j = 2
prvek změní sebe sama (3 za 3)
2 3 4
i = 3, j = 1 (i > j) končí krok
rozdělené pole A je 2 | 3 | 4
všechny části mají jeden prvek a jsou brány za seřazené
část A je dokončena, zbývá část B
5 8 9 7
i = 4, j = 7
pivotem je prvek 8
5 je okay, 7 není okay
i = 5, j = 7
5 8 9 7
prvky se prohodí
5 7 9 8
i = 6, j = 6
9 se prohodí za sebe sama
i = 7, j = 5 (i > j), končí krok, rozdělí se pole
5 7 | 9 8
5 a 7 je okay respektive i = 4, j = 5
pivot je 5, 7 je okay, i = 5, j = 4, rozdělí se pole
5 | 7 -> jsou seřazeny
9 a 8, i = 6, j = 7, pivot je 9
čísla se prohodí a změní se indexy, i = 7, j = 6 -> rozdělí se pole
8 | 9
tím pádem máme 5 | 7 | 8 | 9
část B je rovněž srovnána
celé pole: 1 2 3 4 5 7 8 9

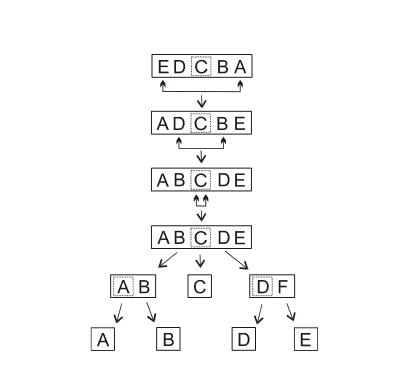
Níže je zachycen ještě jiný postup setřídění pěti písmen s určeným pivotem uprostřed.


obr. 1: Příklad Quicksort - Pivot je prvek "C"
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

Heapsort - třídění haldou

Třídění haldou je v podstatě nejefektivnější algoritmus se složitostí O(n * log n). Tato složitost je zaručená, díky tomu je Heapsort ideální pro použití v real-time systémech.

Halda je specifický typ binárního stromu, v jehož každém uzlu je jeden tříděný prvek. Vlastností těchto prvků je, že prvek v otcovském uzlu má větší hodnotu než prvky uložené v jeho následnících. Ideálním binárním stromem je tzv. vyvážený binární strom, který má všechny vrstvy zaplněné, až na vrstvu poslední, jež jako jediná může být neúplná.


obr. 2: Heapsort - uzly
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

Vrstvou binárního stromu rozumíme množinu uzlů, jež leží na stejné vodorovné úrovni, tedy mají stejnou vzdálenost od kořene. Poslední vrstva je označena jako \(h\), což označuje také výšku haldy. Směrem nahoru se výška logicky snižuje, tedy: \(h - 1, h - 2 \) apod.

Uzly v dané vrstvě \(k\) se označují \(2^k, 2^{k+1}\)... Následnicí v uzlu s indexem \(i\) se značí \(2 * i + 1\) a \(2 * i + 2\), ergo následníci uzlu \(u_i\) jsou \(u_{2 * i + 1}\) a \(u_{2 * i + 2}\).

Výšku haldy zjistíme prostřednictvím vzorce:

\[h = log_2(n)\]

kde \(n\) je počet prvků haldy a \(h\) je zmiňovaná výška.

Následně, zaplníme binární strom tříděnými prvky a budeme odspoda procházet jednotlivé nelistové uzly. Uzly procházíme v pořadí:

\(u_{\frac{n}{2}-1}\), \(u_{\frac{n}{2}-2}\),...., \(u_1\), \(u_2\)

Bude-li hodnota v nelistovém uzlu menší, než hodnota v jeho následníku, prvky prohodíme. Pokračujeme k dalšímu nelistovému uzlu atd. Takto prvky vyměníme tak, aby každý uzel splňoval vlastnost haldy. tj:

Prvek v následníkovi je menší, než prvek v rodičovském uzlu.

V kořenu haldy ve finále musí být největší prvek. Ten vyměníme s prvkem v posledním uzlu haldy a strom o tento list zkrátíme. Takto zkracujeme a měníme prvky, než nám zůstane pouze jeden uzel.

Ukážeme si to na následujícím příkladu. Snazší je podívat se na video :-D

De facto jde o tři věci:

Urovnat haldu do MaxHeap - postupu se říká "heapify"
Vyměnit prvek v kořenu za prvek v posledním listu
Tento list odstranit

mějme nesetříděnou řadu prvků: 7 2 8 1 5 3 9 4
\(n = 8\) a \(log_2(8) = 3\), tedy počet úrovní je 3
indexujeme od 0 a jednotlivé uzly řadíme odshora dolů a zleva doprava


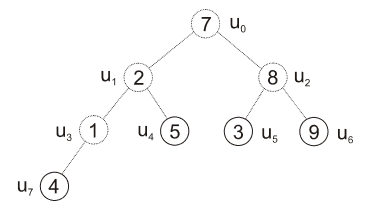obr. 3: Heapsort - tvorba stromu
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

vezmeme poslední z nelistových uzlů \(u_3\) a porovnáme jeho hodnotu s následníkem, \(1 < 4\), ergo prohodíme prvky
další nelistový uzel na řadě je \(u_2\), větší hodnotu má list \(u_6\), vyměníme tyto prvky
následuje \(u_1\) a výměna s jeho největším následníkem \(u_4\)


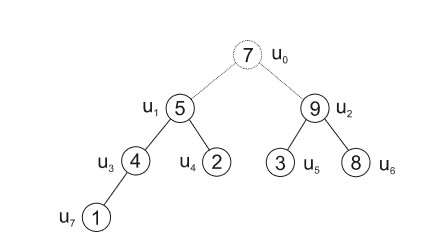obr. 4: Heapsort - výměna prvků v uzlech \(u_3, u_2, u_1\)
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

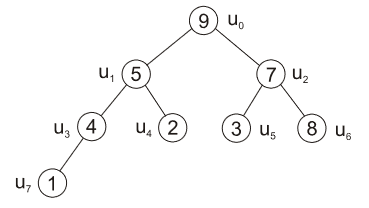
zbývá již jen uzel \(u_0\), vyměníme jeho prvek s prvkem v uzlu \(u_2\)


obr. 5: Heapsort - výměna prvků v uzlech \(u_0\)
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

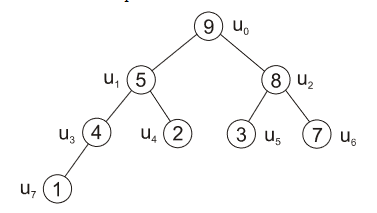
po těchto výměnách nám stále nesplňuje podmínky haldy uzel \(u_2\)
musíme vyměnit prvky mezi \(u_2\) a \(u_6\)


obr. 6: Heapsort - výměna prvků v uzlech \(u_2, u_6\) - hotový strom
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

Nyní můžeme začít třídit :-D

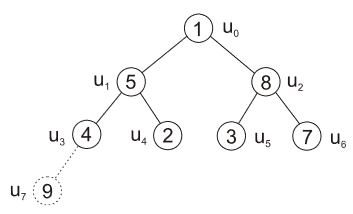
vyměníme prvek kořene s posledním listem a tento list odebereme
zustane nám 7 prvků: 1 5 8 4 2 3 7


obr. 7: Heapsort - odebrání listu \(u_7\)
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

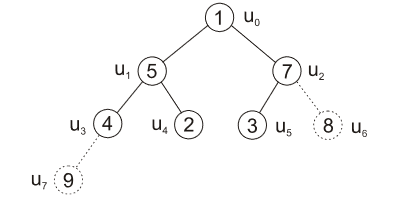
teď je třeba opět strom upravit, tedy prohodit prvky v uzlech \(u_0, u_2, u_6\)
následně vyměnit prvek v kořenu opět za prvek v posledním listu a tento list odebrat


obr. 8: Heapsort - odebrání listu \(u_6\) po předchozí výměně
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

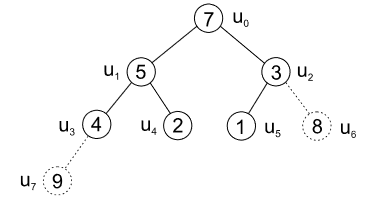
další uzly nesplňují podmínky haldy, tedy je nutné vyměnit prvky mezi uzly \(u_0\) a \(u_2\) a poté \(u_2\) a \(u_5\)


obr. 9: Heapsort - výměna prvků před odebráním listu \(u_5\)
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

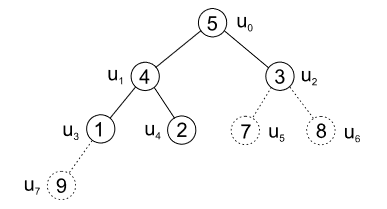
prohodíme prvky 7 a 1 a odebereme list \(u_5\)
opět prohodíme prvky v \(u_0 a u_1, u_3 a u_1\)


obr. 10: Heapsort - výměna prvků před odebráním listu \(u_4\)
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

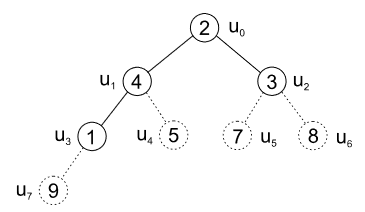
prohodíme prvky v \(u_0\) a \(u_4\) a list \(u_4\) dáme pryč


obr. 11: Heapsort - odebrání listu \(u_4\)
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

vyměníme prvky v \(u_0\) za \(u_1\)
poté kořen s posledním listem \(u_3\) a list dáme pryč
poté prohodíme prvek v \(u_2\) za prvek v kořenu, abychom udrželi podmínky haldy
vyměníme prvek v kořenu za prvek v posledním listu a ten dáme pryč (\(u_2\))
zbývají dva prvky, musíme je opět prohodit, abychom utvořili haldu
poté setřídíme, takže vyměníme zpět a odebereme poslední list \(u_1\)
zbude nám jeden prvek
MÁME SETŘÍDĚNO!


obr. 12: Heapsort - zbytek postupu

ZDROJE

(SKRIPTA) https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf
(VIDEO YT) https://www.youtube.com/watch?v=2DmK_H7IdTo
(WEB) https://www.algoritmy.net/

Státní závěrečné zkoušky - Aplikovaná informatika