Přírodou inspirované optimalizační algoritmy a jejich principy
Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO)
Úvod
Jedná se o sadu algoritmů, imitujících chování přírodních situací. Tedy imitujících chování například zvířat, chemických procesů nebo biologie.
Tyto algoritmy můžeme dělit na dva druhy
- stochastické: Také se jím říká náhodné. Pokud algoritmus vykazuje jakékoliv známky nahodilosti, jedná se o stochastický typ.
- deterministické: Neobsahují nahodilost, můžeme předem určit výsledek.
Obecně lze princip Přírodou inspirovaných optimalizačních algoritmů rozdělit na 4 části:
- Identifikace parametrů populace
- Náhodně vytvoříme iniciální populaci tak, aby pokryla co největší prostor řešení (cíl optimalizační úlohy). Velikost populace je dána tím, jakou optimalizační úlohy chceme řešit (velikost populace je jeden z parametrů).
- Výpočet parametrů populace
- Zjistíme, zdali parametry vybrané v první částí jsou dostatečné ke splnění cíle.
- V této fázi se mění jednotlivé proměnné tak, aby bylo dosaženo toho, že systém je kontrolovaný. Jak se mění parametry, celý systém se přizpůsobuje a aktualizuje směrem k dosažení cíle (pokud samozřejmě měníme parametry dobře).
- Příklad: Umělá kolonie včel bude mít parametry jako jsou zaměstnané včely, kritérium pro opuštění a včelí zvědi. Výběr zdroje jídla a samotný zdroj jídla jsou poté proměnné. Pří výkonu algoritmu upravujeme tyto proměnné.
- Výsledek algoritmu je vyhodnocen. V případě nesplnění cílů optimalizace je možné upravit parametry a začít znovu.
| obr. 1: Obecný princip přírodou inspirovaných optimalizačních algoritmů |
| Převzato z: https://www.tutorialspoint.com/how-to-convert-regular-expression-to-finite-automata |
Particle Swarm Optimization (PSO)
Princip algoritmu je založený na hejnech živočichů, například ptáků. Jedinec tohoto hejna těží z vlastností ostatních jedinců, například při vyhledávání potravy nebo při letu (hejno se pohybuje najednou).
Můžeme si představit, že každý jedinec (particle) hejna (swarm) nám může pomoci najít optimální řešení. Řešení nalezené celým hejnem je poté nejlepším optimálním řešením.
Využití tohoto algoritmu je k nalezení globálního minima.
Princip
Řekněme, že máme nějaký prostor, ve kterém hledáme optimální řešení. V našem případě je tímto optimálním řešením globální minimum nějaké funkce.
Problémem je, že minimum, které nalezneme, nemusí být globální minimum, neb prostor obsahuje lokální minima.
Algoritmus řeší problém pomocí populace částic. Tyto částice jsou prvně rozmístěny náhodně skrz celý prostor popsaný funkcí. Každá tato částice se pohybuje na základě její rychlosti a nejlepšího řešení, které doposud nalezla.
Jedna částice je tedy schopná najít nějaké minimum, ale nemáme žádnou možnost říct, zdali jde o globální minimum.
Jednotlivé částice jsou spolu propojené a sdílí informace o nalezených hodnotách. Pokud nějaký člen hejna / částice najde hodnotu odpovídající lokálnímu minimu, je tato hodnota předána ostatním částicím. Pokud je tato hodnota výhodnější, nežli ta, kterou částice jiná našla, částice to zohlední při směru cesty. Nepostupuje však přímo, dělá tak s jistou odchylkou, protože je možnost, že na své cestě najde ještě více výhodnější hodnotu, kterou poté předá zbytku hejna.
Parametr, který určuje váhu hodnoty nejlepší lokace v řešeném prostoru, musí být menší než 1. Kdyby tomu tak nebylo, tak celé hejno velmi rychle skončí v některém lokálním minimu.
Propojení mezi částicemi může být:
- úplné (každá s každou) propojení může vést ke skončení celého hejna v nějakém lokálním minimu
- částečné (propojeny jsou pouze subsety částic)
Proměnné tohoto algoritmu jsou hodnoty, které udávají, jakým způsobem se bude částice v prostoru pohybovat.
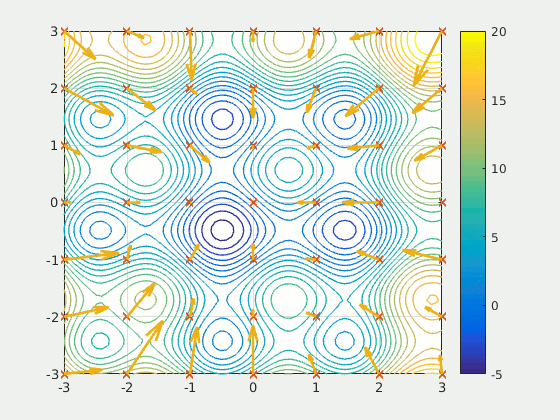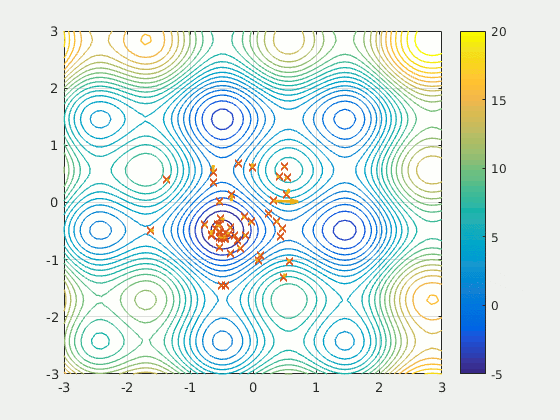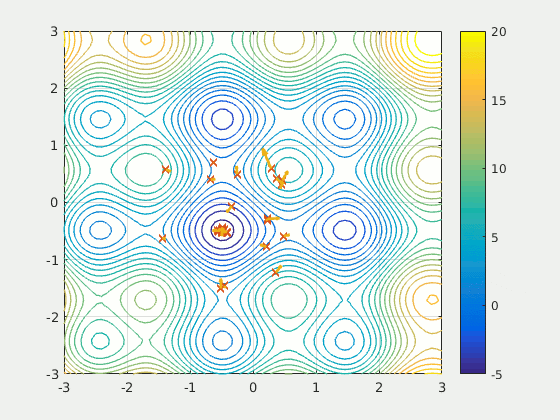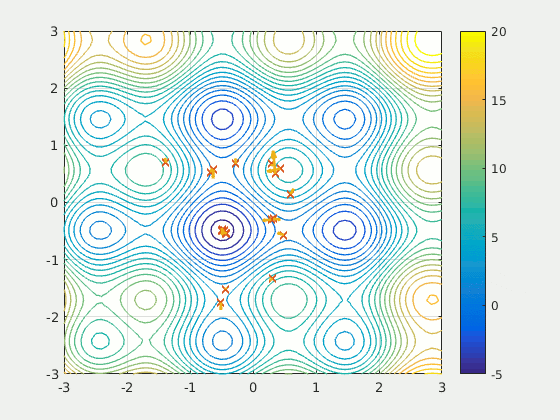 |
|---|
| obr. 2: Vizualizace PSO algoritmu. Všimněme si, jak některé částice i když znají směr udávaný hejnem, nepostupují přímo a pro jiné nemá hodnota nalezena hejnem takovou váhu, jako je funkce udávající jejich pohyb společně s již nalezeným lokálním minimem. |
| Převzato z: https://en.wikipedia.org/wiki/Particle_swarm_optimization |
Ant Colony Optimization (ACO)
Jedná se o probabilistickou optimalizační techniku, která se zaobírá optimalizačními problémy typu nalezení nejkratší cesty.
Algoritmus je inspirován způsobem, jakým mravenci vyhledávají potravu.
Mravenci náhodně cestují, pokud naleznou potravu, odnášejí ji zpět do mraveniště a značkují tuto cestu pomocí feromonů. Pokud nějaký mravenec nalezne tuto cestu, tak s velkou pravděpodobností přestane náhodně cestovat a vydá se po této cestě a posiluje značkovací feromon -> čím více mravenců po cestě cestuje, tím více se tato cesta zdá jako optimálním řešením.
Avšak, tento feromon po nějaké době vyprchá. Pokud je tedy cesta dlouhá, tak feromon vyprchává rychleji, než ho mravenci stíhají doplňovat a cesta již není tak atraktivní, což umožňuje mravencům opět náhodně cestovat a mít možnost najít kratší cestu, kde bude feromon vyprchávat pomaleji.
Nyní si uvedeme základní algoritmus s rodiny Ant Colony Optimization algoritmů, který se nazývá Ant system.
Princip
Pro aplikování algoritmu je nutné optimalizační problém převést na hledání minimální cesty ve váženém grafu.
Jednotlivé váhy hran mohou odpovídat vzdálenostem mezi uzly, které tyto hrany spojují.
Algoritmus se skládá ze 3 kroků, které jsou v cyklu.
- Každý mravenec najde nějaké svoje řešení optimalizační úlohy. Při první iteraci je pravděpodobnost vybrání konkrétní cesty z bodu X do bodu Y stejná pro všechny tyto cesty (hrany). Mravenec tedy najde cíl (jídlo) "náhodou". Cestou pokládá feromon (zvyšuje atraktivitu cesty).
- Nyní se musí mravenec vrátit. Cesta s největší atraktivitou má větší probabilitu že bude vybrána. Tedy i ti mravenci, kteří dorazili do cíle po delší cestě, se mohou vrátit kratší cestou -> buď náhodou nebo díky tomu,že je na ni více feromonu (je více atraktivní). Tím, jak se mravenci vracejí, zároveň posilují atraktivitu cesty.
- Nyní skončil jeden cyklus a v grafu se nacházejí cesty, s různou atraktivitou. Hodnota atraktivity a všech cestách je nyní aktualizována, aby byl simulován úbytek feromonu. Úbytek feromonu závisí na:
- proměnné určující úbytek
- délce cesty (delší cesta, větší úbytek)
V dalších iteracích je už více pravděpodobné, že si mravenci vyberou cestu, která obsahuje více feromonu. Mravenec se rozhoduje kudy půjde na základě dvou kritérií:
- atraktivita: síla feromonu (tady to voní fakt dobře, tam něco bude)
- zkušenost: když jsem šel předtím tudy, tak jsem našel jídlo (cíl úlohy)
Tyto vlastnosti přispívají k pravděpodobnosti, že si mravenec cestu vybere. Je zde tedy vždy možnost, že si mravenec vybere cestu jinou, čímž je možnost, že objeví cestu kratší. Pokud by byla cesta opravdu kratší, mravenec má šanci, že po této cestě půjde znovu i v další iteraci -> zkušenost a bude pokládat feromon -> atraktivita jak pro něj, tak pro potenciální další mravence. Kratší cesta také znamená, že se úbytek feromonu skrz iterace je kratší. Tímto je řešen problém lokálního minima.
Využití tohoto algoritmu se prvně objevilo jako cíl řešení optimalizační úlohy Problém obchodního cestujícího. Dnes se dá využít na optimalizační úlohy, kde nás zajímá nejkratší cesta (síťování, doprava).
Variace algoritmu
Existují další variace, s lehce upraveným postupem, hlavně v oblasti aktualizace feromonu a způsobu výběru cesty jednotlivcem v každé iteraci.
- Ant colony system (ACS): Pouze nejlepší mravenec (ten, který nalezl v konkrétní iteraci nejlepší řešení) může aktualizovat váhy pomocí aplikace globálního pravidla pro aktualizaci feromonů.
- Elitist ant system: Krom toho, že mravenci posilují atraktivitu cest, tak globálně nejlepší řešení (cesta) si sama vytváří malé množství feromonu, i když po ni žádný mravenec nešel.
- Max-min ant system (MMAS): Pouze globálně nejlepší řešení a lokálně nejlepší řešení (nejlepší řešení konkrétní iterace) mohou přidávat feromon a zvyšovat tím svoji atraktivitu. Pro zamezení stagnace je nastavena minimální a maximální hodnota, kterou mohou cesty mít. Na začátku algoritmu je hodnota feromonu na všech cestách maximální.
- Rank-based ant system (ASrank): Pouze omezené množství mravenců (x nejlepších řešení v iteraci) může přidat feromon na cesty, kterými prošlo. Kratší cesty mezi uzly získávají více feromonu.
- Parallel ant colony optimization (PACO): Mravenci jsou rozděleni do skupin, které jsou schopné se spolu dorozumívat.
- a pár dalších...
Zdroje
- An Introduction to Nature-inspired Optimization Algorithms (NIOAs). Mobarak Inuwa [online] @2022 [citováno 16.05.2023].
Dostupné z: https://www.analyticsvidhya.com/blog/2022/11/an-introduction-to-nature-inspired-optimization-algorithms-nioas/ - Particle swarm optimization. Wikipeida: The Free Encyclopedia [online] @2023 [citováno 16.05.2023].
Dostupné z: https://en.wikipedia.org/wiki/Particle_swarm_optimization - Introduction to Ant Colony Optimization GeeksForGeeks [online] @2021 [citováno 16.05.2023].
Dostupné z: https://www.geeksforgeeks.org/introduction-to-ant-colony-optimization/ - Ant colony optimization algorithms. Wikipeida: The Free Encyclopedia [online] @2023 [citováno 16.05.2023].
Dostupné z: https://en.wikipedia.org/wiki/Ant_colony_optimization_algorithms