Učení neuronové sítě

Cíl, pojmy: zevšeobecnění, přeučení, problém uváznutí v lokálním minimu, trénovací, testovací, validační množina

Činnost neuronových sítí lze rozdělit do dvou fází:

Učení (adaptace)
Života

Ve fázi učení se znalosti ukládají do synaptických vah neuronové sítě, lze to znázornit jako:

\[\frac{\delta W}{\delta t} \neq 0\]

kde \(W\) je matice všech synaptických vah a \(t\) je čas. Synaptické váhy se v průběhu učení mění.

Fáze života:

\[\frac{\delta W}{\delta t} = 0\]

v této fázi se získané znalosti využívají ve prospěch řešení nějakého problému. Synaptické váhy se v této fázi nemění.

Definice učení

Jde de facto o proces získávání / uchování znalostí, založený na změně synaptických vah měnících se dle pravidel determinovaných typem učení neuronové sítě.
Učením se rozumí adaptace neuronové sítě, které po této fázi bude nositelkou znalostí získaných v průběhu učení.
jedná se o optimalizační úlohu, která najde pro příslušnou trénovací množinu dat takovou konfiguraci vah, kdy je průměrná chyba sítě přes celou trénovací množinu menší, než požadované kritérium.

Učení lze realizovat deduktivní a induktivní metodou, přičemž u induktivní metody se vyvozují generalizovaně platné závěry na základě pozorování množiny jevů (syntetický přístup k učení). Deduktivní metoda využívá pouze jeden jev a jeho pozorování a analyzování (analytický přístup k učení).

Nejčastější metodou učení u neuronových sítí je metoda induktivní, a to buď s učitelem - poskytuje správnou informaci o požadovaném výstupu NS, nebo bez učitele - NS nedostává informaci o požadovaném výstupu, ale odvozuje si ji sám na základě zpětné vazby.

Učení NS se dále provádí prostřednictvím gradientních metod či přírodou inspirovaných algoritmů (genetický algoritmus).

Pojmy související s učením NS

Trénovací množina: množina vzorů určená k trénování neuronové sítě - nacházení vztahu mezi vstupy a výstupy (provádí regresní analýzu, čímž se učí)
Testovací množina: množina vzorů určená pro testování neuronové sítě - určení kvality naučeného systému
Vzor: element datového souboru určeného pro zpracování NS
- Vzor bývá v páru - vstupní vektor (na vstupech neuronové sítě), výstupní vektor (požadovaná hodnota výstupů)
- sítě SOM (Samoorganizující se mapy) výstupní vektor nepotřebují
Validační množina: množina vzorů použita k testování přímo v průběhu učení - zabraňuje se tak přeučení NS; používá se pro případnou změnu parametrů učení, aby se předešlo overfittingu-přeučení; vyhodnocuje-li systém se shodnou úspěšností trénovací i validační množinu, je pravděpodobně správně naučen; pokud systém vykazuje vyšší úspěšnost u vyhodnocení trénovací množiny, je nejspíše přeučený
Vybavení: předložení jednoho vzoru NS a výpočet výstupu NS
Iterace: předložení vzoru NS, provedení Vybavení a následně jednoho kroku učení
Epocha: provedení iterace pro všechny vzory z trénovací množiny
Učení: proces výpočtu váhových synaptických koeficientů/vah na základě trénovací množiny
- učení se skládá z epoch
Přeučení: nadměrná doba učení - je provedeno příliš mnoho epoch učení
- toto způsobuje nadměrnou chybu pro netrénovaná data (zhorší se zevšeobecnění)
Lokální minimum: parazitní minimum na chybové/energetické hyperploše, jehož chyba je větší než chyba globálního minima
Zevšeobecnění: schopnost NS správně reagovat na neučená data
Hebbovo pravidlo: pro úpravu vah, posiluje vztahy mezi neurony, jež vykazují podobné reakce na stejné podněty
Delta pravidlo: pro úpravu vah v učícím algoritmu Back Propagation

Hebbův zákon učení

Hebbův zákon je základním prvkem téměř všech algoritmů učení NS (vyjma Back Propagation). Hebbův zákon popisuje algoritmus modifikace hodnot synaptických vah v nervových systémech živých organismů. Je založen na předpokladu, že jsou-li dva navzájem propojené neurony ve stejném okamžiku aktivní, tak jejich vzájemná vazba je zesílena. V opačném případě (nejsou-li aktivní) se vazba mezi nimi oslabuje. Je-li aktivní pouze jeden neuron synapse nejsou modifikovány.

Neurony mají tedy dva stavy: aktivní a neaktivní.

Vzorec Hebbova zákona

\[\Delta W_{ij} = \eta \times x_i (t) \times x_j(t)\]

\(\Delta W_{ij}\) - rozdíl vah
\(x_j\) - presynaptický stav j-tého neuronu
\(x_i\) - postsynaptický stav i-tého neuronu
\(\eta\) - eta, zrychlení/zesílení procesu učení

Algoritmus učení NS (s učitelem)

Náhodně inicializujeme váhy v neuronové síti
Vezmeme pár vektorů I/O z trénovací množiny dat a vstupní vektor přiložíme na vstup sítě
Vypočteme výstupy sítě
Porovnáme výstup sítě z částí výstup z páru I/O a vypočteme odchylku
Na základě odchylky upravíme váhy sítě \(w\)
Dokud nevyčerpáme celou trénovací množinu, pokračujeme bodem 2
Pokud je průměrná chyba přes celou trénovací množinu vyšší, než požadované kritérium, pokračujeme opět bodem 2
Síť je naučena, KONEC

GRADIENT

Diferenciální operátor (řecky nabla, symbol \(\nabla\)). Je-li aplikován na funkci o vícero proměnných, je jejím výsledkem vektor parciálních derivací dle všech proměnných této funkce.

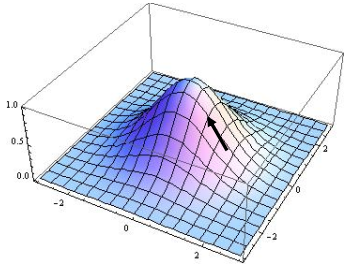
**GRADIENT** je směr největšího růstu funkce v daném bodě na ploše funkce f.


obr. 1: Gradient
zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.

Uváznutí v lokálním minimu (Gradientní metoda učení)

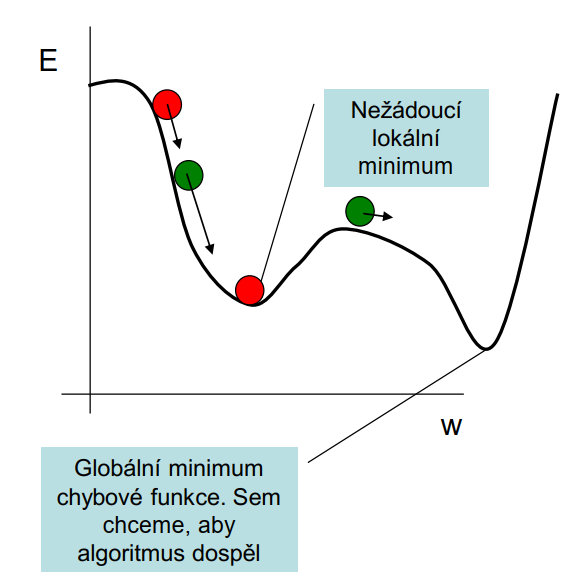
Představme si kuličku reprezentující hodnoty všech vah a kutálející se dle gradientu E, tj. dle gradientu se přičte ke každé váze \(\Delta w\) dle hodnoty gradientu násobeného parametrem \(\eta\) - viz Delta pravidlo v otázce č. 1.15 (Učení neuronové sítě metodou s učitelem).

Dospěje-li kulička do lokálního minima, krok kterýmkoli směrem znamená navýšení chyby. Za "kopec" do globálního minima kulička nevidí (algoritmus nevidí) a tudíž končí s chybou lokálního minima.


obr. 2: Problém lokálního minima
zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.

Řešení uváznutí v lok. minimu

Častým řešením může být zavedení setrvačnosti (parametr \(\alpha\)). Kulička získá setrvačnost a nezávisle na gradientu se překulí přes svah do globálního minima. Setrvačnost musí být dostatečná, aby mohla kulička svah překonat, jinak bude oscilovat v lokálním minimu, dokud se nezastaví.

Správné nastavení parametrů \(\eta\) a \(\alpha\)
Výběr vzorů s trénovací množiny v náhodném pořadí
- obvykle se používá sekvenční (postupný) výběr vzorů, kdy se pořadí vzorů nemění v průběhu epochy. Toto někdy vede „mylným závislostem“, které si neuronová sít během učení vyvodí a to může někdy vést do lokálního minima (odpovíte stejně rychle na otázku kolik je 6x9 nebo 9x6)
Strukturou trénovací množiny - stejné zastoupení vzorů ve všech třídách a zředění dat (vynechání obdobných vzorů v rámci kategorie)
Použití gradientní metody s proměnným krokem (mění se parametr \(\eta\)), je-li parametr stejný, považujeme krok algoritmu za konstantní

Trénovací množina

Příprava trénovací množiny

dostupná data rozdělíme na testovací a trénovací množinu
vzory ze všech tříd by měly mít stejné procentní zastoupení
normalizace vstupních dat
- změna měřítka
- transformace skrze nelineární funkci: potlačení velkých hodnot, zdůraznění malých hodnot

Popis a vzorec

Trénovací množina obsahuje prvky popisující řešený problém, přičemž každý vzor trénovací množiny popisuje jakým způsobem jsou excitovány neurony vstupní a výstupní vrstvy.

Formálně lze za trénovací množinu \(T\) považovat množinu prvků (vzorů), které jsou definovány uspořádanými dvojicemi takto:

\[T = {(x_k t_k) | x_k \in {0, 1}_n, t_k \in {0, 1}_m, k = 1, ...q}\]

\(q\): počet vzorů trénovací množiny
\(x_k\): vektor excitací vstupní vrstvy tvořené n neurony
\(t_k\): vektor excitací výstupní vrstvy tvořené m neurony

ZDROJE

SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.
OLEJ, Vladimír a Hájek PETR. Úvod do umělé inteligence: Moderní přístupy - Distanční opora. Univerzita Pardubice: Fakulta Ekonomicko-správní, 2010, 95s. ISBN 978-80-7395-307-2.
VOLNÁ, Eva. Neuronové sítě 1. 2 vyd. Ostrava: Ostravská univerzita v Ostravě, 2008, 87 s. Dostupné také z: https://web.osu.cz/~Volna/Neuronove_site_skripta.pdf

Státní závěrečné zkoušky - Aplikovaná informatika