Učení neuronové sítě metodou s učitelem
Princip algoritmu zpětného šíření chyby - Backpropagation, parametry algoritmu, delta pravidlo
Učení s učitelem je primárně založeno na minimalizaci chyby mezi aktuální a požadovanou odezvou neuronové sítě. Právě ona odezva sítě zde hraje roli učitele.
Hledaná funkce je zde vždy zadána prostřednictvím dvojice hodnot, hodnot vstupů \(x_k\) a hodnot požadovaných výstupů \(t_k\). Během procesu učení nám síť vrací skutečné výstupní hodnoty \(y_k\) coby výstupní odezvu NS na daný vstupní signál. Zároveň dochází k úpravě vah za účelem minimalizace chyby, respektive dosažení co největší shody mezi skutečným výstupem a tím požadovaným.
Cílem samotného učení je hledání minima chybové (energetické) funkce:
\[E(w) = \sum_{l = 1}^q E_l (w)\]
- \(q\): počet vzorů trénovací množiny
- \(l\): \(l.\) tréninkový vzor
- \(w\): konfigurace vah v dané NS
Je to součet parciálních chyb sítě \(E_l(w)\) vzhledem k jednotlivým tréninkovým vzorům.
Parciální chyba neuronové sítě \(E_l(w)\) pro \(l.\) tréninkový vzor (\(l = 1, ...., q\)) je úměrná součtu mocnin odchylek (rozdílů) skutečných hodnot výstupu sítě \(y_k\) pro vstup \(l\)-tréninkového vzoru od požadovaných hodnot výstupů u tohoto vzoru \(t_k\):
\[E_l(w) = \frac{1}{2}\sum_{k \in {Y}} (y_k - t_k)^2\]
ZÁPIS - PŘEDNÁŠKY SKRBEK: \[E_l(w) = \frac{1}{2}\sum_{j=1}^M \sum_{i=1}^N (y_i^{(j)} - d_i^{(j)})^2\]
- N: počet výstupů neuronové sítě
- M: počet vzorů v trénovací množině
- \(y_i^{(j)}\): i-tý výstup j-tého vzoru z trénovací množiny
Vícevrstvá neuronová síť a algoritmus BACKPROPAGATION
Vícevrstvá NS je nejrozšířenější variantou propojení neuronů se sigmoidní aktivační funkcí (způsob jakým se ze vstupu počítá výstup neuronu). Zatímco algoritmus Backpropagation (zpětné šíření chyby) je nejrozšířenějším adaptačním algoritmem v těchto vícevrstvých neuronových sítích.
Vícevrstvá síť má vstupní vrstvu \(X\), skrytou vnitřní vrstvu \(Z\) a výstupní vrstvu neuronů \(Y\). Jednotlivé neurony jsou značeny:
- \(X_i, i = 1, ..., n\)
- \(Z_j, j = 1, ..., p\)
- \(Y_k, k = 1, ..., m\)
Neurony ve výstupní a vnitřní vrstvě musí mít definovaný tzv. Bias, který odpovídá váhové hodnotě přiřazené spojení mezi příslušným neuronem a fiktivním neuronem, jehož aktivace je vždy 1.
Označení Bias pro j-tý neuron ve vnitřní vrstvě je \(v_{0}{j}\) a ve výstupní vrstvě k-tého neuronu \(W_{0}{k}).
Vícevrstvou NS tvoří vždy minimálně tři vrstvy, přičemž mezi dvěma sousedními vrstvami se nachází tzv. úplné propojení neuronů, které znamená, že každý neuron nižší vrstvy je propojen se všemi neurony vrstvy vyšší.
| obr. 1: Vícevrstvá neuronová síť |
| zdroj: VOLNÁ, Eva. Neuronové sítě 1. 2 vyd. Ostrava: Ostravská univerzita v Ostravě, 2008, 87 s. Dostupné také z: https://web.osu.cz/~Volna/Neuronove_site_skripta.pdf. |
Problémy modelu vícevrstvé NS s Backpropagation
- Minimalizace chybové funkce
- Volby vhodné topologie sítě
- volba vhodného počtu neuronů ve vnitřních vrstvách
- volba počtu vrstev (většinou 1-2 vrstvy)
- příliš malá síť s algoritmem BP skončí v mělkém lokálním minimu (je třeba doplnit další neurony)
- Složitější architektura může vést naopak k přeučení (špatné generalizaci)
Algoritmus BACKPROPAGATION
Jak již bylo řečeno, tento algoritmus je využíván v přibližně 80 % všech aplikací NS. Algoritmus obsahuje 3 etapy:
- feedforward (dopředné) šíření vstupního signálu treninkového vzoru
- zpětné šíření chyby
- aktualizaci váhových hodnot na spojeních mezi neurony
Během první fáze obdrží každý neuron ve vstupní vrstvě \(X_i, i = 1, ..., n\) signál/vstup \(x_i\) a zařídí jeho přenos ke všem neuronům skryté vrstvy \(Z_1, ..., Z_p\). Každý neuron ve skryté vrstvě vypočítá svou aktivaci \(z_j\) a předá tento signál neuronům ve vrstvě výstupní. Každý neuron ve výstupní vrstvě spočítá také svoji aktivaci \(y_k\) - odpovídá skutečnému výstupu (k-tého neuronu) po předložení vstupního vzoru. Tímto vznikne zpětná vazba a je nutná adaptace NS - aktualizace vah.
Vzorec algoritmu BP a odvození: \[\frac{\delta E}{\delta w_{ij}} = \frac{\delta E}{\delta y_i} \centerdot \frac{\delta y_i}{\delta \varphi_i} \centerdot \frac{\delta \varphi_i}{\delta w_{ij}}\]
to odpovídá následujícímu vzorci:
\[\frac{\delta E}{\delta w_{ij}} = -(d_i - y_i) \centerdot y_i(1 - y_i) \centerdot x_j\]
- \(y_i(1 - y_i)\) je derivací aktivační funkce - sigmoidy
- \((d_i - y_i)\) rozdíl mezi požadovaným výstupem \(d_i\) a reálným výstupem \(y_i\)
- \(x_j\) je vstup
- \(-(d_i - y_i) \centerdot y_i(1 - y_i) \centerdot x_j\) \(\iff\) chyba připadající na i-tý neuron \(\iff\) \(\delta_i\)
Gradientní metoda a Delta pravidlo - aktualizace vah
Pro optimalizaci vah a minimalizaci chybové funkce se využívá tzv. gradientní metody (také viz. GRADIENT a LOKÁLNÍ MINIMUM v otázce č. 14 - Učení neuronové sítě).
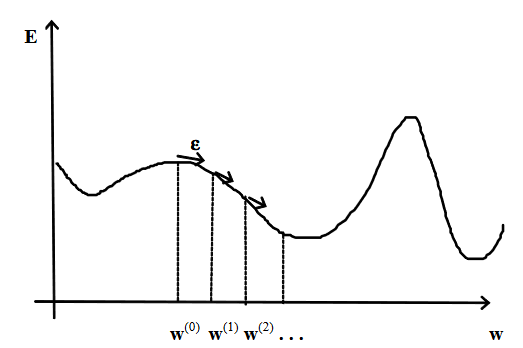 |
|---|
| obr. 2: Gradientní metoda |
| zdroj: VOLNÁ, Eva. Neuronové sítě 1. 2 vyd. Ostrava: Ostravská univerzita v Ostravě, 2008, 87 s. Dostupné také z: https://web.osu.cz/~Volna/Neuronove_site_skripta.pdf. |
Vertikální osa \(E\) nám zachycuje chybovou funkci, která určuje chybu sítě vzhledem k pevné tréninkové množině a v závislosti na konfiguraci sítě. Hledáme konfiguraci vah \(w\), při které je chybovost minimální.
Na ose \(x\) máme znázorněn mnohorozměrný vektor vah \(w\).
- náhodně zvolíme konfiguraci sítě v bodě \(w^0\) - chybovost je velká
- v tomto bodě sestrojíme tečný vektor (GRADIENT)
- posuneme se po tomto vektoru dolů o vzdálenost \(\varepsilon\)
- získáme novou konfiguraci \(w^1\) = \(w^0 + \Delta w^1\), pro kterou je chybovost menší
- opakujeme dokud se nedostaneme do lokálního (ideálně globálního) minima
\[\Delta w = - \eta \nabla E\]
- \(\eta\): (eta) rychlost učení <0, 1>
Delta pravidlo
\[\Delta w_{ij} (t) = \eta * \delta_i (t) x_j + \alpha \Delta w_{ij} (t-1)\]
- \(\Delta w_{ij}\): změna vah mezi i-tým a j-tým neuronem
- \(\eta\): (eta) rychlost učení <0, 1>
- \(\delta_i\): připadající na i-tý neuron
- \(x_j\): j-tý vstup neuronu
- \(\alpha\): (alfa) moment/setrvačnost <0, 1)
Parametr \(\alpha\) nám udává jakou měrou se má do změny váhy započítat změna předchozí. Změna váhy má dvě složky:
- chybu odezvy sítě, započítávající se koeficientem rychlosti učení
- předchozí změnu váhy
Pokud je změna váhy malá, dominuje složka chyby sítě. Pokud je tomu obráceně a chyba sítě klesne, je váha stále upravována ve velikosti předchozí změny. Setrvačnost může pomoci dostat se z lokálního minima a nalézt lepší konfiguraci vah s menší chybou.
Parametr \(\eta\) určuje o kolik se má upravit váha neuronu (relativně k velikosti chyby). Čím větší koeficient, tím rychleji se síť učí. Nicméně, příliš vysoká hodnota může vést k oscilacím a ideálního řešení nemusí být dosaženo.
Zpětná propagace chyb do skrytých vrstev
\[\delta_i = y_i (1 - y_i) \sum^N_{k-1} w_{ki} \delta_k\]
- \(N\): počet neuronů v následující vrstvě, tedy vrstvě blíže k výstupu
- \(\delta_k\): dle předchozí logiky by se mělo jednat o chybovost k-tého neuronu (tedy neuronu skryté vrstvy) - pokud bychom to převedli na obrázek č. 1, tak se jedná o chybovost j-tého neuronu Z
Průběh chyby během učení
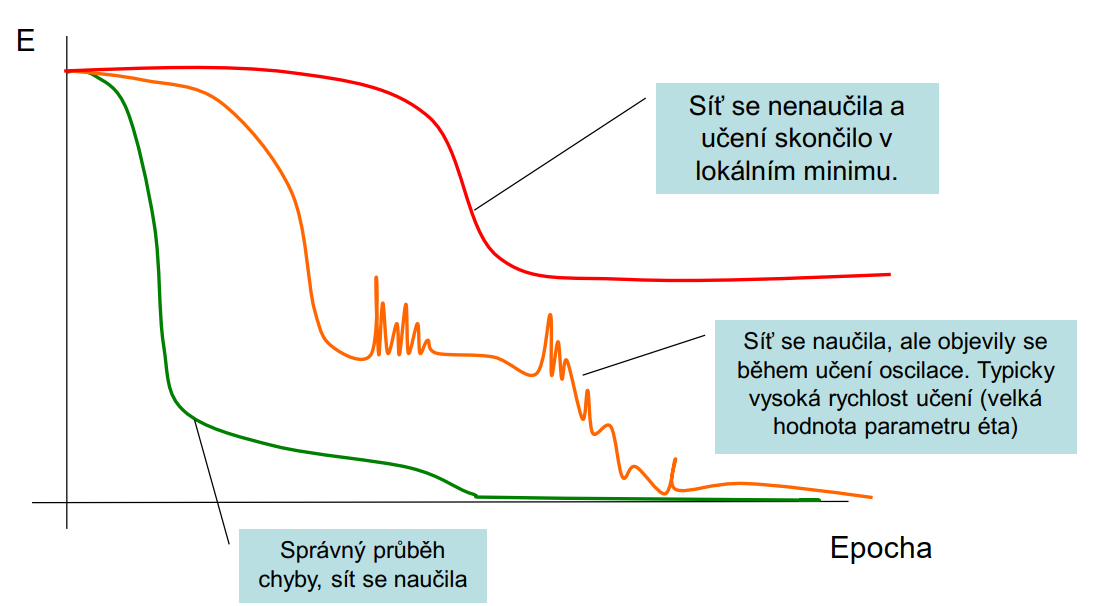 |
|---|
| obr. 3: Průběh chyby během učení |
| zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška. |
ZDROJE
- SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.
- VOLNÁ, Eva. Neuronové sítě 1. 2 vyd. Ostrava: Ostravská univerzita v Ostravě, 2008, 87 s. Dostupné také z: https://web.osu.cz/~Volna/Neuronove_site_skripta.pdf.
- OLEJ, Vladimír a Hájek PETR. Úvod do umělé inteligence: Moderní přístupy - Distanční opora. Univerzita Pardubice: Fakulta Ekonomicko-správní, 2010, 95 s. ISBN 978-80-7395-307-2.