Fuzzy množina a fuzzy logika
funkce příslušnosti, fuzzy pravidla, fuzzyfikace, inference a defuzzyfikace
Fuzzy logika vs tradiční logika
V klasické logice máme pouze dva stavy: 1 nebo 0, true nebo false. Ve fuzzy logice je stav interpretován na stupnici od 0 do 1. Stav může být tedy například 0,3, 0,7 nebo 1 -> může být neurčitý.
Ale stav čeho?
Funkce příslušnosti
Definice: reprezentuje úroveň pravdivosti určité vlastnosti
- Vlastnost se vztahuje k zkoumané veličině. Zkoumanou veličinou může být například teplota. Jaká může být teplota? Může být teplo, chladno, nebo tak nějak normálně. Nebo to může být vzdálenost. Jsme blízko, daleko, středně daleko. Nebo i riziko půjčky klientovi. Velké, střední, malé. Tradiční logika je na vše z toho schopná odpověď jen ano, nebo ne. Riziko půjčky? - ano/ne. Teplota - ano, je teplo; ne, není teplo. Vzdálenost - ano, jsme blízko; ne, jsme daleko.
Na obrázku pod je uveden příklad funkce příslušnosti pro vlastnost chladno. Nebo třeba vlastnost pomalu pokud se fuzzy systémem snažíme řídit rychlost. Pro účely této otázky budeme řídit teplotu v domácnosti.
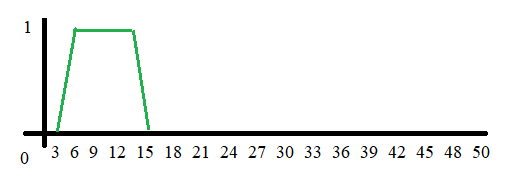 |
|---|
obr. 1: Funkce příslušnosti. Na ose x jsou vstupní hodnoty a na ose y úroveň pravdivosti |
| Vlastní zdroj |
Funkcí pravdivosti můžeme mít i více -> v závislosti na tom, kterou veličinu fuzzyfikujeme. Naše teplota má 3 funkce pravdivosti.
 |
|---|
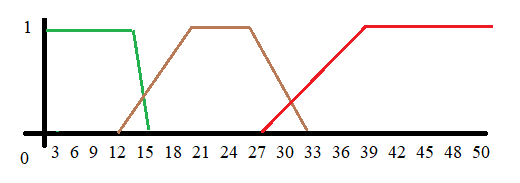
obr. 2: 3 funkcí příslušnosti pro veličinu teplota: chladno - zelená, normálně - hnědá, horko - červená |
| Vlastní zdroj |
Můžeme se na to koukat následovně:
- Když je 6 stupňů, tak je zima, jakmile se dostaneme na 12 stupňů, tak už přestává být zima a začíná být normálně, normálně je na 21 stupňů. Jak se blížíme k 30 stupňům, přestává být normálně a začíná být horko a vše nad 39 stupňů už je horko.
Ale jak jsme přišli na tyhle hodnoty? Vymyslely jsme si je. V reálném světe se používají expertní fuzzy systémy.
- Jsou to fuzzy systémy, ve kterých experti na daný obor určili, jaké hodnoty daná funkce příslušnosti pokrývá. Jednotlivé prvky množiny vstupních hodnot mají povětšinou strukturu typu "Když je hodnota taková, tak patří do téhle funkce příslušnosti" (například: když je hodnota
3,tak jechladno). - K fuzyfikaci se vztahují problémy tzv. přechodů. Tedy například je třeba rozhodnout, s jakou mírou pravdivosti je pravda, že když je hodnota
14, tak je chladno. Ze vstupní množiny je třeba tím pádem také rozpoznat, v jakých hodnotách se tyto přechody nacházejí.
Ale k čemu nám to je?
Fuzzyfikace
Umožní nám vzít vstup do systému a přeměnit ho na set, jež obsahuje míru pravdivosti se kterou se vstupní hodnota vztahuje k funkcím příslušnosti.
Definice: jedná se o proces přeměny vstupní hodnoty na fuzzy množinu
Řekněme, že našim naměřeným vstupem je 27 stupňů. Výstupem fuzzyfikace je poté set, který obsahuje hodnoty toho, jak moc hodnota 27 odpovídá jednotlivým funkcím příslušnosti. Pro 27 stupňů je to tedy [0; 0,7; 0,2].
Vstupní hodnota je nyní fuzzyfikovaná, tuto hodnotu, využijeme při inferenci.
Inference a fuzzy pravidla
Jedná se o proces vyhodnocování vstupů do našeho fuzzy systému, za pomocí setu fuzzy pravidel.
Fuzzy pravidla si určujeme při návrhu systému (nebo je upravíme později) a mají následující strukturu:
IF teplota IS chladno THEN klimatizace IS vypnuta.
Toto byl jen příklad pravidla, povětšinou máme celý set, který se vyhodnocuje najednou. Pro náš příklad si vytvoříme tento set:
- IF teplota IS chladno THEN klimatizace IS vypnuta
- IF teplota IS normální THEN klimatizace IS málo
- IF teplota IS horko THEN klimatizace IS hodně
Můžeme si všimnout, že najednou tu máme jakousi klimatizaci a její vlastní množinu funkcí příslušnosti. Je to kvůli dalšímu kroku, defuzzyfikaci, která ním umožní určit výstup systému.
Každé fuzzy pravidlo nám vrátí hodnotu. V našem jednoduchém případě, kdy má každé pravidlo jen jednu podmínku (žádné AND nebo OR), tak je jednoduché je vyhodnotit. Výstupem je další set, obsahující míry pravdivostní, tentokrát však pro pravou stranu pravidel, tedy pro klimatizaci a její funkce příslušnosti.
Protože se jedná o velmi jednoduchý příklad, tak tento set má opět tvar
[0; 0,7; 0,2]. Toto se moc často neděje, povětšinou jsou fuzzy pravidla složitější a výsledek inference se značně liší od vstupu.
Defuzzyfikace
Tento krok se zabývá převedením setu mír příslušností (fuzzy množiny) získaného skrze inferenci na číslo. Pro defuzzyfikaci máme vlastní funkce příslušnosti, v našem případě jde o rychlost otáček větráku klimatizace v procentech.
 |
|---|
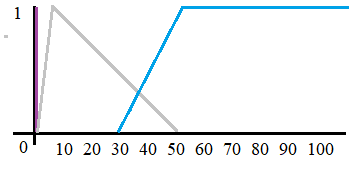
obr. 3: 3 funkce příslušnosti pro veličinu klimatizace: vypnuto - fialová, málo - šedá, horko - modrá |
| Vlastní zdroj |
Našim úkolem je nyní namapovat hodnoty získané skrze inferenci tak, abychom dostali výstupní hodnotu, která nám bude říkat, jak se má výsledný řízený systém chovat.
Je spoustu způsobů, jak toto provést, ale populárním a používaným způsobem je oseknout funkce příslušnosti podle získané fuzzy množiny a spočítat střed nově vzniklého útvaru.
Defuzzyfikace podle naši fuzzy množiny vypadá následovně:
 |
|---|
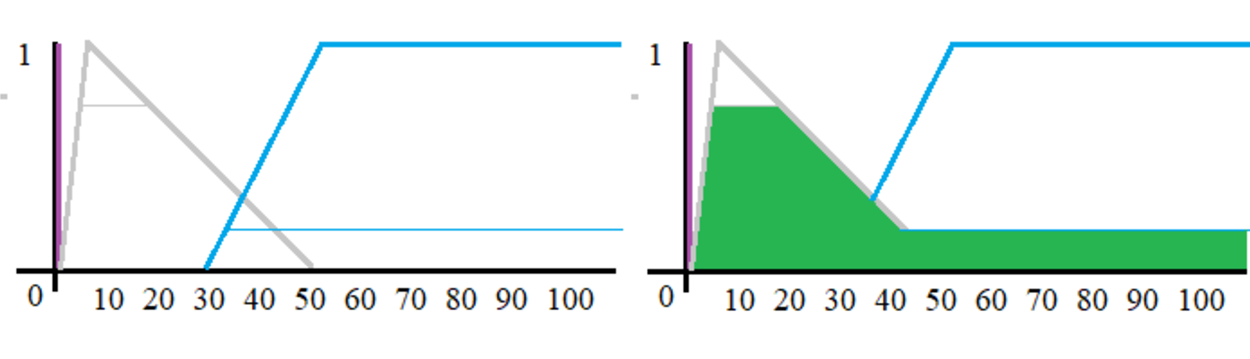
| obr. 4: Určení limitu pro oseknutí - vlevo a výsledný útvar, jehož střed je výsledkem - vpravo |
| Vlastní zdroj |
Výsledkem je, že při teplotě 27 stupňů budou otáčky klimatizace cca 30%.
Defuzzyfikace, je narozdíl od fuzzyfikace výpočetně náročnější, hlavně díky kroku převádění fuzzy množiny na číslo.
Celý proces by se dal popsat jako mapování vstupních veličin na výstupní veličiny.
| obr. 5: Schéma systému s přidanou zpětnou vazbou |
| Dostupné z: https://www.researchgate.net/figure/Architecture-of-fuzzy-logic-control_fig1_337511172 |
Výhody fuzzy logiky oproti IF tvrzení
Jeden by si mohl říct, že je stejná věc by se dala udělat i přes pár IFů v Javě. Koneckonců, fuzzy pravidla jsou také IF tvrzení.
- IF tvrzení se stanou ve složitějších případech až příliš komplikovaná, zde byl uvedený příklad s jedním vstupním parametrem (teplota) v případě více vstupních parametrů jsou jednotlivé závislosti mnohem složitější na modelaci pomoci IF tvrzení (například modelování závislosti dýška v restauraci na základě kvality jídla a kvality obsluhy).
- Fuzzy pravidla jsou modulární, můžeme je lehce upravit a přizpůsobit tak systém změnám v budoucnu.
- Nemusíme znát podrobně celý systém, pro který fuzzy pravidla vytváříme. Stačí nám vědět, co chceme řídit. Návrh fuzzy systému můžeme klidně začít od inferenční části.
Využití
Fuzzy systémy se dají využít k nepřebernému množství úkonů, hlavně díky tomu, že umí pracovat s neurčitostí.
- řízení systému v reálném čase (náš příklad)
- modelování závislostí
- zpracování obrazu (získání kontur, kdy zjišťujeme, jestli pozice linek vůči sobě odpovídá danému natočení)
- rozpoznávání hlasu
- a hodně dalších, dostupných například zde
Zdroje
- Fuzzy logic. Wikipedia: The Free Encyclopedia [online] @2023 citováno [17.05.2023]
Dostupné z: https://en.wikipedia.org/wiki/Fuzzy_logic - Difference between Fuzzification and Defuzzification. GeeksForGeeks [online] @2023 citováno [17.05.2023]
Dostupné z: https://www.geeksforgeeks.org/difference-between-fuzzification-and-defuzzification/ - An Introduction to Fuzzy Logic. Tim Arnett [online] @2015 citováno [17.05.2023]
Dostupné z: https://www.youtube.com/watch?v=rln_kZbYaWc - What Is Fuzzy Logic?. Matlab [online] @2022 citováno [17.05.2023]
Dostupné z: https://www.youtube.com/watch?v=__0nZuG4sTw - Fuzzy Logic - Computerphile. Computerphile [online] @2014 citováno [17.05.2023]
Dostupné z: https://www.youtube.com/watch?v=r804UF8Ia4c