Pojem algoritmus a jeho složitost

Definice algoritmu, časová a paměťová složitost, časová složitost a třídy P a NP, příklady časových složitostí. Klasifikace algoritmů podle použitého paradigmatu (přístupu), principy těchto paradigmat.

Pojem Algoritmus

Algoritmem rozumíme schématický postup řešení určitého problému, přičemž tento postup je realizován prostřednictvím konečného množství přesně definovaných kroků.

Pojem algoritmus nemusí být využit jen v informatice, ale ve všech oblastech reálného života. Za algoritmus můžeme považovat klidně také recept v kuchařce (algoritmus vaření určitého jídla).

Vlastnosti algoritmů

  1. Konečnost - algoritmus má konečný počet kroků

  2. Určitost/determinovanost - všechny kroky algoritmu jsou přesně definovány

  3. Korektnost - algoritmus skončí pro korektní (libovolná data) správným výsledkem, a to v konečném množství kroků

  4. Obecnost - algoritmus řeší obecnou třídu daných problémů respektive všechny úlohy daného typu

  5. Elementárnost - algoritmus se skládá z jednoduchých kroků, které neumožňují žádný osobitý výklad

  6. Univerzálnost - algoritmus má definovanou celou škálu/množinu vstupních dat, s nimiž umí pracovat

  7. Rezultativnost - algoritmus má alespoň jeden výstup, který je v požadovaném vztahu k zadaným vstupům

  8. Efektivita - algoritmus by měl k výsledku dojít nejbezpečněji, nejsnáze a s co možná nejmenšími náklady na strojový čas

Dělení algoritmů

A. Deterministické a nedeterministické

  1. Deterministický - v každém svém kroku má algoritmus právě jen jednu možnost jak pokračovat dále

  2. Nedeterministický - algoritmus má více možností v jednotlivých krocích jak pokračovat

B. Rekurzivní a iterativní

  1. Iterativní - v tomto algoritmu se opakuje určitá jeho část/blok

  2. Rekurzivní - algoritmus opakuje kód pomocí volání sebe sama (řešení podproblémů)

    • každý rekurzivní algoritmus může být převeden do iterativní podoby - převod řeší kompilátor předmětného programovacího jazyka
    • rekurzivní algoritmy mají výhodu v čitelném a kompaktním zápisu
    • nevýhodou je naopak dodatečný spotřebovaný strojový čas při jednotlivých rekurzivních voláních

PŘÍKLADY

Iterativní algoritmy: bubble sort a insertion sort
Rekurzivní algoritmy: merge sort a quick sort

C. Sériové, paralelní a distribuované algoritmy

  1. Sériový algoritmus - vykonává všechny kroky v sérii za sebou

  2. Paralelní algoritmus - vykonává kroky naráz v různých vláknech

  3. Distribuovaný algoritmus - vykonává kroky rovněž naráz, ale na více strojích

Složitost algoritmu

Třídy složitosti

  1. P - nejzákladnější třída složitosti. obsahuje všechny problémy řešitelné pomocí deterministického Turingova stroje v polynomiálním čase např. nejkratší cesta, minimální kostra grafu.

  2. NP - nedeterministicky polynomiální - řeší problémy v polynomiálním čase na nedeterministickém Turingově stroji (umí rozvětvit každý krok do dvou částí a řešit problém na obou větvích současně). Složitostní třída P je v této třídě obsažena.

    • co-NP - Jazyk L (úloha) je v této třídě právě tehdy, je-li doplněk jazyka L ve třídě NP. U NP úloh lze polynomiálně ověřit ANO instanci, zatímco u co-NP úloh lze ověřit pouze NE instanci.

      (Zde to chápu jako TRUE/FALSE, je-li výsledek kroku FALSE, tak jeje lze ověřit v polynomiálním čase).

  3. NPC - NP complete, nebo-li NP úplná je třída složitosti obsahující nejtěžší úlohy ze třídy NP (problém obchodního cestujícího, problém batohu, problém dvou loupežníků).

  4. co-NPC - Jazyk (úloha) L je ve třídě co-NPC právě tehdy, je-li doplněk tohoto jazyka ve třídě NPC.

  5. NP-hard - takové úloha je redukovanou NPC úlohou, u které zároveň nevíme zda je obsahem třídy NP. NP-hard úlohy jsou minimálně stejně těžké jako všechny NPC úlohy.

  6. PSPACE a NPSPACE - Jazyk L je ve třídě PSPACE právě tehdy, když existuje deterministický Turingův stroj, který pracuje s polynomiální paměťovou složitostí (tj. nepoužije žádnou paměťovou buňku na indexu vyšším než p(n)) a přijímá jazyk L.

    Jazyk L je ve třídě NPSPACE právě tehdy, když existuje nedeterministický Turingův stroj, který pracuje s polynomiální paměťovou složitostí a přijímá jazyk L.

A. Časová složitost

Skutečná složitost algoritmu se nedá v mnoha případech zcela přesně spočítat. Závisí na tom, jak algoritmus implementujeme a na jakém stroji a s jakým HW jej provádíme. Pro určení složitosti si pomáháme odhadem (v matematice terminus technicus).

Všeobecně můžeme ke zjištění složitosti přistoupit několika způsoby:

  1. Zjistit počet elementárních operací
  2. Zjednodušit výpočet na elementární operace nad daty
  3. Dále zjednodušit na počet porovnání

Primárně nás zajímá, jak se bude algoritmus chovat pro velké vstupy/instance problému. De facto jde o vyjádření řádu růstu funkce složitosti algoritmu. Tomuto říkáme asymptotická (časová) složitost, tedy asymptoticky se blíží k dané hodnotě, typicky (-> ∞).

Každému algoritmu lze jednoznačně přiřadit neklesající funkci zvanou asymptotická (časová) složitost, která charakterizuje počet operací algoritmu v závislosti na rostoucím obsahu vstupních dat.

ČÍM POMALEJI TATO FUNKCE ROSTE, TÍM JE ALGORITMUS RYCHLEJŠÍ.

Asymptotická složitost
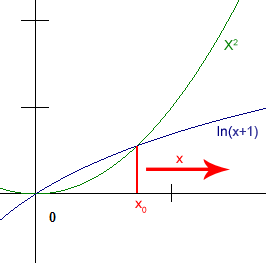
obr. 1: Asymptotická složitost - osa X (velikost vstupních dat), Y (zatížení systému)
zdroj: https://www.algoritmy.net/image/id/35908

U rozdělení algoritmů do tříd složitosti (dle klasifikace nazývané asymptotická složitost) platí, že od určité velikosti dat je asymptoticky lepší algoritmus vždy rychlejší, než algoritmus horší asymptotické třídy bez ohledu na to, zda je některý z počítačů k-násobně výkonnější.

Tento fakt je dobře vidět na obrázku č. 1. Pokud bychom vynásobili jakoukoli konstantou k funkci X2, tj. zrychlovali bychom PC, na němž tento algoritmus běží, tak vždy bude existovat nějaký bod x0, od kterého bude algoritmus popsaný logaritmickou funkcí ln(x + 1) vždy rychlejší.

Asymptotickou složitost značíme tzv. Landauovou notací - "Omikron notací" nebo také "Velké O notací".

Běžné složitosní funkce

  • O(n) - lineární
  • O(n2) - kvadratická
  • O(n3) - kubická
  • O(log n) - logaritmická
  • O(2n) - exponenciální
  • O(1) - konstantní (provede se pouze konstantně mnoho kroků)

Chování jednotlivých funkcí

Porovnání funkcí
obr. 2: Růst jednotlivých funkcí
zdroj: http://pruvodce.ucw.cz/static/pruvodce.pdf

Pokud bychom zaznamenali odhady, jak dlouho poběží algoritmy s uvedenými složitostmi na dnešním průměrném PC (pro rok 2022), jenž vykoná cca 109 operací za sekundu. Vypadalo by to následovně:

Časové porovnání algoritmů
obr. 3: Doby běhu algoritmů s různou složitostí
zdroj: http://pruvodce.ucw.cz/static/pruvodce.pdf

Z obrázku 3 je zřejmé, že exponenciální algoritmus je extrémně složitý a i pro relativně malý vstup bude běh programu tak dlouhý, že budou všichni mrtví Dave! Také proto se algoritmům s exponenciální složitostí snažíme vyhnout. Jediné efektivní opodstatnění má algoritmus s touto složitost v Cyber-Security, a to pro účely šifrování citlivých údajů.

B. Prostorová (paměťová) složitost

Dle paměťové složitosti měříme paměťové nároky algoritmu. K tomu potřebujeme vědět, kolik nejvíce elementárních paměťových buněk bude v každém okamžiku běhu algoritmu použito. V běžných programovacích jazycích (C či Rust) za elementární buňku považujeme například proměnnou typu int, float, byte nebo pointer. Elementární velikosti však nemají pole nebo textove řetězce.

C. Průměrná složitost

Oproti předchozím složitostem, kde jsme uvažovali nejhorší možný scénář (složitost), zde nás zajímá aritmetický průměr časových/prostorových nároků algoritmu přes všechny vstupy dané velikosti.

Průměrnou složitost používáme tehdy, když algoritmus povětšinou doběhne rychle, ale existují tzv. anomální vstupy, pro něž je předmětný algoritmus velmi pomalý.

D. Složitost problému

Je třeba rozlišovat mezi Složitostí algoritmu a Složitostí problému. Složitost algoritmu je odhadem složitosti právě pro onen algoritmus (zajímá nás horní odhad nebo průměrný případ).

U Složitosti problému nás zajímá složitost nejlepšího algoritmu, který problém vyřeší. Zde používáme dolní odhad. Víme-li, že problém P je řešitelný algoritmem s asymptotickou složitostí s(n) a umíme-li dokázat, že neexistuje jiný algoritmus, který by problém vyřešil s lepší časovou složitostí, než s(n). Poté je můžeme říci, že složitost problému P je s(n).

ZDROJE