Úvod

Cílem této knihy je shromáždit na jednom místě základní informace z celého spektra oboru Informační technologie a speciálně pak z oblasti Embedded systémů. Tyto informace by měly posloužit především studentům oboru Aplikovaná informatika na Přírodovědecké fakultě Jihočeské univerzity v Českých Budějovicích (a doufejme že stejně dobře i studentům příbuzných oborů na jiných univerzitách), při studování na Státní závěrečné zkoušky.

Struktura knihy vychází ze Seznamů zkušebních okruhů pro SZZ:

Šíření obsahu - licence

Tato kniha a tedy i šíření jejího obsahu podléhá licenci Creative Commons Uveďte původ 4.0 Mezinárodní License.

Přispívání

Software

Pro participaci na tvorbě materiálů je třeba mít nainstalovaný GIT a jakýkoliv textový editor (ideálně VSCodium či jiný editor s podporou VS Code Extensions).

Proces publikování vytvořených materiálů zajišťuje CLI nástroj mdBook (ke stažení zde). Po rozbalení archivu je ideální přidat cestu k binárce do PATH, poté není při volání nutné udávat celou její cestu.

Nastavení prostředí

Klonování repozitáře

git clone https://codeberg.org/atlas144/szz.git

VS Code Extensions

Pokud používáte editor s podporou VS Code Extensions, doporučujeme nainstalovat tyto:

Markdown All in One
Code Spell Checker
Czech - Code Spell Checker
- je nutné upravit Předvolby > Nastavení > cSpell.language na en,cs
Better TOML

Postup

Řekněme, že budeme zpracovávat okruh 2.1.5. Soubor instrukcí (2.1.5. je číslo kapitoly, viz seznam).

Příprava

V repozitáři vytvoříme novou větev v větve main s názvem 2-1-5-soubor-instrukci:

Nová větev

Poté stáhneme změny pomocí

git pull

a přesuneme se do nově vytvořené větve.

git checkout 2-1-5-soubor-instrukci

Obsah

Nyní můžeme začít upravovat soubor pro daný okruh. Zdrojové soubory se nachází ve složce ./src a následujících podsložkách podle předmětu. Zde Informační a komunikační technologie > Architektura počítačů > Soubor instrukcí, cesta tedy je ./src/ikt/ap/soubor-instrukci.md.

Přidáváme-li obrázky či jiný dodatečný obsah, vytvoříme složku s názvem okruhu (zde tedy ./src/ikt/ap/soubor-instrukci) a obsah přidáváme do ní.

V průběhu editace je užitečné vidět finální podobu dokumentu. K tomu slouží náhledy v editoru:

Tlačítko náhledu ve VSCodium

Rovněž si lze výslednou podobu prohlédnou přímo pomocí mdBook, a to spuštěním příkazu

mdbook serve -o             # pokud je lokace v PATH
[cesta]/mdbook serve -o     # pokud se binarka spousti primo

Změny je dobré průběžně commitovat a pushovat na server!

git commit -m "feat(content): lorem ipsum"
git push

Formát zápisu

Obsah je zapisován ve formátu Markdown s rozšířeními, která jsou popsána zde.

Pro zápis matematických výrazů lze použít MathJax (s drobnými omezeními).

Zdroje

Zdroje přidáváme nakonec souboru, v samostatné sekci. Ideální formát je citace podle normy ČSN ISO 690. Minimální formát je odkaz na web.

Konec editace

Považujeme-li okruh za dokončený, pushneme změny a následně otevřeme pull request ze zpracovávané větve (2-1-5-soubor-instrukci) do main:

Nový pull request

Po schválení se nově zpracovaný okruh objeví na stránce.

Pojem algoritmus a jeho složitost

Definice algoritmu, časová a paměťová složitost, časová složitost a třídy P a NP, příklady časových složitostí. Klasifikace algoritmů podle použitého paradigmatu (přístupu), principy těchto paradigmat.

Pojem Algoritmus

Algoritmem rozumíme schématický postup řešení určitého problému, přičemž tento postup je realizován prostřednictvím konečného množství přesně definovaných kroků.

Pojem algoritmus nemusí být využit jen v informatice, ale ve všech oblastech reálného života. Za algoritmus můžeme považovat klidně také recept v kuchařce (algoritmus vaření určitého jídla).

Vlastnosti algoritmů

Konečnost - algoritmus má konečný počet kroků
Určitost/determinovanost - všechny kroky algoritmu jsou přesně definovány
Korektnost - algoritmus skončí pro korektní (libovolná data) správným výsledkem, a to v konečném množství kroků
Obecnost - algoritmus řeší obecnou třídu daných problémů respektive všechny úlohy daného typu
Elementárnost - algoritmus se skládá z jednoduchých kroků, které neumožňují žádný osobitý výklad
Univerzálnost - algoritmus má definovanou celou škálu/množinu vstupních dat, s nimiž umí pracovat
Rezultativnost - algoritmus má alespoň jeden výstup, který je v požadovaném vztahu k zadaným vstupům
Efektivita - algoritmus by měl k výsledku dojít nejbezpečněji, nejsnáze a s co možná nejmenšími náklady na strojový čas

Dělení algoritmů

A. Deterministické a nedeterministické

Deterministický - v každém svém kroku má algoritmus právě jen jednu možnost jak pokračovat dále
Nedeterministický - algoritmus má více možností v jednotlivých krocích jak pokračovat

B. Rekurzivní a iterativní

Iterativní - v tomto algoritmu se opakuje určitá jeho část/blok
Rekurzivní - algoritmus opakuje kód pomocí volání sebe sama (řešení podproblémů)
- každý rekurzivní algoritmus může být převeden do iterativní podoby - převod řeší kompilátor předmětného programovacího jazyka
- rekurzivní algoritmy mají výhodu v čitelném a kompaktním zápisu
- nevýhodou je naopak dodatečný spotřebovaný strojový čas při jednotlivých rekurzivních voláních

PŘÍKLADY

Iterativní algoritmy: bubble sort a insertion sort
Rekurzivní algoritmy: merge sort a quick sort

C. Sériové, paralelní a distribuované algoritmy

Sériový algoritmus - vykonává všechny kroky v sérii za sebou
Paralelní algoritmus - vykonává kroky naráz v různých vláknech
Distribuovaný algoritmus - vykonává kroky rovněž naráz, ale na více strojích

Složitost algoritmu

Třídy složitosti

P - nejzákladnější třída složitosti. obsahuje všechny problémy řešitelné pomocí deterministického Turingova stroje v polynomiálním čase např. nejkratší cesta, minimální kostra grafu.
NP - nedeterministicky polynomiální - řeší problémy v polynomiálním čase na nedeterministickém Turingově stroji (umí rozvětvit každý krok do dvou částí a řešit problém na obou větvích současně). Složitostní třída P je v této třídě obsažena.
- co-NP - Jazyk L (úloha) je v této třídě právě tehdy, je-li doplněk jazyka L ve třídě NP. U NP úloh lze polynomiálně ověřit ANO instanci, zatímco u co-NP úloh lze ověřit pouze NE instanci.
  
  (Zde to chápu jako TRUE/FALSE, je-li výsledek kroku FALSE, tak jeje lze ověřit v polynomiálním čase).
NPC - NP complete, nebo-li NP úplná je třída složitosti obsahující nejtěžší úlohy ze třídy NP (problém obchodního cestujícího, problém batohu, problém dvou loupežníků).
co-NPC - Jazyk (úloha) L je ve třídě co-NPC právě tehdy, je-li doplněk tohoto jazyka ve třídě NPC.
NP-hard - takové úloha je redukovanou NPC úlohou, u které zároveň nevíme zda je obsahem třídy NP. NP-hard úlohy jsou minimálně stejně těžké jako všechny NPC úlohy.
PSPACE a NPSPACE - Jazyk L je ve třídě PSPACE právě tehdy, když existuje deterministický Turingův stroj, který pracuje s polynomiální paměťovou složitostí (tj. nepoužije žádnou paměťovou buňku na indexu vyšším než p(n)) a přijímá jazyk L.

Jazyk L je ve třídě NPSPACE právě tehdy, když existuje nedeterministický Turingův stroj, který pracuje s polynomiální paměťovou složitostí a přijímá jazyk L.

A. Časová složitost

Skutečná složitost algoritmu se nedá v mnoha případech zcela přesně spočítat. Závisí na tom, jak algoritmus implementujeme a na jakém stroji a s jakým HW jej provádíme. Pro určení složitosti si pomáháme odhadem (v matematice terminus technicus).

Všeobecně můžeme ke zjištění složitosti přistoupit několika způsoby:

Zjistit počet elementárních operací
Zjednodušit výpočet na elementární operace nad daty
Dále zjednodušit na počet porovnání

Primárně nás zajímá, jak se bude algoritmus chovat pro velké vstupy/instance problému. De facto jde o vyjádření řádu růstu funkce složitosti algoritmu. Tomuto říkáme asymptotická (časová) složitost, tedy asymptoticky se blíží k dané hodnotě, typicky (-> ∞).

Každému algoritmu lze jednoznačně přiřadit neklesající funkci zvanou asymptotická (časová) složitost, která charakterizuje počet operací algoritmu v závislosti na rostoucím obsahu vstupních dat.

ČÍM POMALEJI TATO FUNKCE ROSTE, TÍM JE ALGORITMUS RYCHLEJŠÍ.


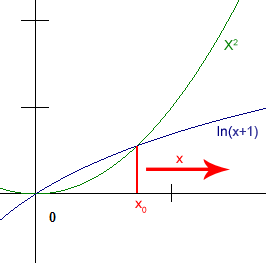
obr. 1: Asymptotická složitost - osa X (velikost vstupních dat), Y (zatížení systému)
zdroj: https://www.algoritmy.net/image/id/35908

U rozdělení algoritmů do tříd složitosti (dle klasifikace nazývané asymptotická složitost) platí, že od určité velikosti dat je asymptoticky lepší algoritmus vždy rychlejší, než algoritmus horší asymptotické třídy bez ohledu na to, zda je některý z počítačů k-násobně výkonnější.

Tento fakt je dobře vidět na obrázku č. 1. Pokud bychom vynásobili jakoukoli konstantou k funkci X², tj. zrychlovali bychom PC, na němž tento algoritmus běží, tak vždy bude existovat nějaký bod x₀, od kterého bude algoritmus popsaný logaritmickou funkcí ln(x + 1) vždy rychlejší.

Asymptotickou složitost značíme tzv. Landauovou notací - "Omikron notací" nebo také "Velké O notací".

Běžné složitosní funkce

O(n) - lineární
O(n²) - kvadratická
O(n³) - kubická
O(log n) - logaritmická
O(2ⁿ) - exponenciální
O(1) - konstantní (provede se pouze konstantně mnoho kroků)

Chování jednotlivých funkcí


obr. 2: Růst jednotlivých funkcí
zdroj: http://pruvodce.ucw.cz/static/pruvodce.pdf

Pokud bychom zaznamenali odhady, jak dlouho poběží algoritmy s uvedenými složitostmi na dnešním průměrném PC (pro rok 2022), jenž vykoná cca 10⁹ operací za sekundu. Vypadalo by to následovně:


obr. 3: Doby běhu algoritmů s různou složitostí
zdroj: http://pruvodce.ucw.cz/static/pruvodce.pdf

Z obrázku 3 je zřejmé, že exponenciální algoritmus je extrémně složitý a i pro relativně malý vstup bude běh programu tak dlouhý, že budou všichni mrtví Dave! Také proto se algoritmům s exponenciální složitostí snažíme vyhnout. Jediné efektivní opodstatnění má algoritmus s touto složitost v Cyber-Security, a to pro účely šifrování citlivých údajů.

B. Prostorová (paměťová) složitost

Dle paměťové složitosti měříme paměťové nároky algoritmu. K tomu potřebujeme vědět, kolik nejvíce elementárních paměťových buněk bude v každém okamžiku běhu algoritmu použito. V běžných programovacích jazycích (C či Rust) za elementární buňku považujeme například proměnnou typu int, float, byte nebo pointer. Elementární velikosti však nemají pole nebo textove řetězce.

C. Průměrná složitost

Oproti předchozím složitostem, kde jsme uvažovali nejhorší možný scénář (složitost), zde nás zajímá aritmetický průměr časových/prostorových nároků algoritmu přes všechny vstupy dané velikosti.

Průměrnou složitost používáme tehdy, když algoritmus povětšinou doběhne rychle, ale existují tzv. anomální vstupy, pro něž je předmětný algoritmus velmi pomalý.

D. Složitost problému

Je třeba rozlišovat mezi Složitostí algoritmu a Složitostí problému. Složitost algoritmu je odhadem složitosti právě pro onen algoritmus (zajímá nás horní odhad nebo průměrný případ).

U Složitosti problému nás zajímá složitost nejlepšího algoritmu, který problém vyřeší. Zde používáme dolní odhad. Víme-li, že problém P je řešitelný algoritmem s asymptotickou složitostí s(n) a umíme-li dokázat, že neexistuje jiný algoritmus, který by problém vyřešil s lepší časovou složitostí, než s(n). Poté je můžeme říci, že složitost problému P je s(n).

ZDROJE

Abstraktní datové struktury

definice, užití a implementace, zásobník, fronta, prioritní fronta, lineární spojové seznamy

Každá hodnota, všechna data zpracovávaná v PC musí být nějakého typu. Typ je dán užitým programovacím jazykem.

Typ proměnné nám určuje 3 věci:

množinu hodnot, které je možné daným typem vyjádřit
vnitřní reprezentaci v PC - jakou zabírá paměť
přípustné operace, jež lze nad danou hodnotou provést

Definice

Datová struktura definuje konkrétní způsob organizace dat v paměti počítače, tak aby ona data mohla být využita efektivně. Datová struktura umožňuje spravovat a uchovat množinu dat stejného typu (případně různých typů, ale logicky souvisejících).

Užití a vlastnosti

Datové struktura umožňuje data:

vkládat
vyhledávat
aktualizovat
mazat

DS bývají většinou založeny na na schopnosti PC ukládat/načítat data kamkoli do paměti, určené pointerem.

Kritériem pro návrh datové struktury je:

rychlost čtení dat
rychlost zápisu (vložení, mazání, aktualizace)
náročnost na paměť
náročnost implementace - komplikovaný algoritmus má větší pravděpodobnost chybovosti

Např. DB spoléhají na binární stromy, dle nichž spravují indexy.

Lineární spojový seznam

dynamická datová struktura
obsahuje více datových položek (stejného typu)
položky jsou navzájem provázány pomocí ukazatelů nebo referencí
důležité je, že poslední položka odkazuje "nikam", tím poznáme konec seznamu

Lineární seznamy mohou být jednosměrné nebo obousměrné. V jednosměrném odkazuje položka na následující. V obousměrném odkazuje položka do předchozí i následující.

Lineární seznam může být také kruhový -> poslední prvek listu odkazuje na první prvek.

Fronta a prioritní fronta

dynamická datová struktura
DS typu FIFO
v OS se tento typ DS nazývá PIPE (roura)
poslední položka odkazuje nikam (tímto poznáme konec fronty)
lze je implementovat pomocí pole, nebo spojového seznamu (linkedList)
složitost je O(n)
implementace pomocí haldy (prioritní fronta) může dosahovat složitosti O(log n)

Princip fronty

zajímají nás jen první a poslední položka fronty
INSERT (enqueue) a DELETE (dequeue) (push(), take(), pop(), apod.)
zleva "naláduju" frontu -> přidávám prvky/bloky zleva, takže poprvé vložený prvek je zcela vpravo:

mějme čísla 3 5 4 6
push(5); push(3); push(6); push(4)
fronta bude vypadat takto: 4 6 3 5
každý příkaz pro dequeue (take()) - bude bez parametru a metoda odebere zleva poslední prvek (který byl "pušnutý" jako první); v tomto případě 5
fronta bude: 4 6 3

Princip prioritní fronty

implementace pomocí binární haldy
pracuje s tzv. prioritou
- push() s danou prioritou
- take() - odstraní z fronty nejstarší prvek s nejvyšší prioritou
prvek se de facto vkládá tak, že se projdou priority stávající a na příslušné místo se umístí námi přidávaný prvek (heapsort)
- přeruší se link/vazba mezi předchozím a následujícím prvkem a vytvoří se 2 nové vazby na vložený prvek

Zásobník - Stack

pro dočasné ukládání dat
založen na LIFO (Last is First Out)
pro manipulaci se používá tzv. ukazatel zásobníku, který ukazuje na poslední vloženou položku zásobníku (vrchol zásobníku)
uživatel smí používat pouze několik málo příkazů: push(), pop()
zásobník má dno (počáteční adresa zásobníku)
vrchol (nejvyšší zabraná paměťová buňka)

Implementace je možná pomocí pole, nebo linkového seznamu.

Stack je část paměti počítače, jež má pevně danou počáteční adresu, ale proměnlivou strukturu.

počáteční velikost stacku je 0
pointer velikosti zásobníku ukazuje na počáteční adresu
dáme-li push() - tak se přidají data na adresu paměti, na kterou pointer ukazuje, ale adresa pointeru se změní (navýší/zmenší se) o velikost paměti zabranou daty
pop() nebo pull() vyjme data z adresy paměti, na kterou ukazuje pointer, adresa pointeru se změní o velikost paměti, kterou data zabírala

PŘÍKLAD

Počáteční adresa zásobníku je pevně stanovená, např. na 1000 a expandujeme směrem dolů. Měníme-li velikost zásobníku, tak nám adresa pointeru (znázorňující aktuální velikost stacku) bude dekrementovat až do 0 (v závislosti na velikosti dat). Tedy, do zásobníku přidám float (32 bitů), adresa pointeru vrcholu zásobníku se změní na 968. Dále přidám data adresa pointeru se dekrementuje na třeba 740. Takto mohu postupovat až do nuly. Budu-li data ze zásobníku brát, tak se adresa pointeru bude inkrementovat zpět k 1000.

Underflow - ukazatel vecholu zásobníku nikdy nesmí být inkrementován nad původní hranici - jinak hrozí podtečení
Overflow - pokud budeme volat naopak stále metodu push() tak nám může dojít k přetečení tím, že adresa pointeru se dekrementuje přes hodnotu 0

Zdroje

Základní řadící algoritmy

Selection sort, Insertion sort, Bubble sort, Heap sort, Quick sort - popis, složitost

Řadící algoritmy slouží k řazení vstupních dat (prvků vstupního souboru) dle velikosti, je jedno zda vzestupně či sestupně. Základními operacemi jsou srovnání a přesun. Při výběru řadicího algoritmu je třeba mít na paměti několik kritérií:

Časová složitost
Implementační složitost
Vhodnost pro danou datovou strukturu
Stabilita algoritmu

Časová složitost a implementace

Nejvýkonnějšími algoritmy jsou ty, které neporovnávají jednotlivé hodnoty prvků, ale fungují na jiném principu řazení (složitost O(n)) např:

Counting sort - řazení počítáním četnosti jednotlivých hodnot
Radix sort - číslicové řazení (řadí řetězce fixní délky dle jednotlivých znaků)

Ani jeden z výše uvedených algoritmů však není vhodný pro všeobecné použití.

Algoritmy pro univerzální použití třída O(n * log(n)):

Pro malá vstupní data jsou vhodnější algoritmy s jednoduchou implementací a s kvadratickou složitostí O(n²):

Nejvýkonnější algoritmus s kvadratickou složitostí je Shell sort.

Stabilita algoritmu

Stabilní algoritmus je takový, u nějž nedojde během řazení k prohození dvou prvků se stejnou hodnotou. Jako příklad užitečnosti stability algoritmu může pýt řazení žáků v třídní knize dle jména a příjmení. Stabilní algoritmus seřadí jména Bruno Semerek a Vrundo Semerek s prvním v pořadí Bruno Semerek. Nestabilní algoritmus by při druhém řazení mohl výsledky zpětně přehodit (Vrundo Semerek, Bruno Semerek).

Přirozenost algoritmu

Přirozený algoritmus rychleji zpracuje již částečně seřazenou posloupnost dat.

Třídění na místě

Algoritmus třídí prvky na místě, pokud prvky neopouštění paměťové buňky, v nichž byly zadány. Nicméně, algoritmus může využít tzv. pracovní buňky, kam si ukládá číselné proměnné (indexy, parametry...) tato uložená data jsou pomocnou pamětí algoritmu.

Tabulka níže zachycuje jednotlivé třídící algoritmy včetně jejich složitosti a jiných vlastností. Pro účely SZZ bude poslední kapitola otázky věnována funkcionalitě každého algoritmu, u nějž je poznámka NAUČIT SE.

Srovnání třídících algoritmů

Název	CZ Název	Přirozený	Stabilní	Složitost	Poznámka
Bubble sort	Bublinkové	ANO	ANO	O(n²)	NAUČIT SE
Shakesort	-	ANO	ANO	O(n²)
Selection sort	Výběrem	NE	NE	O(n²)	NAUČIT SE
Insertion sort	Vkládáním	ANO	ANO	O(n²)	NAUČIT SE
Shell sort	Schellovo	ANO	NE	O(n²)
Heapsort	Haldou	NE	NE	O(n log(n))	NAUČIT SE
Merge sort	Slučováním	ANO	ANO	O(n log(n))
Quicksort	Rychlé	NE	NE	O(n log(n))	NAUČIT SE
Radix sort	Číslicové	NE	ANO	O(n)
Counting sort	Počítání četnosti	NE	ANO	O(n)
Bucket sort	Přihrádkové	-	ANO	O(n * k)
Comb sort	Hřebenové	ANO	NE	O(n²)

zdroje:
https://www.algoritmy.net/article/75/Porovnani-algoritmu
https://cs.wikipedia.org/wiki/%C5%98adic%C3%AD_algoritmus

Skupiny třídících algoritmů

1. Vnitřní třídění

Základní vlastností algoritmů tzv. vnitřního třídění je, že všechny tříděné prvky jsou uloženy ve vnitřní paměti počítače (Registry, RAM, Cache aj.). Výhodou vnitřního třídění je, že veškeré operace (srovnání či přesuny) probíhají pouze nad hodnotami v interní paměti.

Dle základní operace PŘESUNU dělíme algoritmy třídění do tří skupin:

Vkládáním - Insertion sort, Shell sort
Výměnou - Bubble sort, Quicksort
Výběrem - Selection sort

U třídění vkládáním zvětšujeme posloupnost tím, že vkládáme jednotlivé prvky na příslušná místa.

U třídění výměnou třídíme posloupnost záměnou dvou vybraných prvků , až dosáhneme úplného setřídění.

U třídění výběrem postupně vybíráme jednotlivé prvky ze vstupu a přidáváme je k postupně tříděné posloupnosti.

Specifickou metodou vnitřního třídění je třídění haldou, kde halda je binárním stromem. jehož prvky se de facto vyměňují.

Jednoduché metody vnitřního třídění - PŘÍMÉ

Účinější metody vnitřního třídění

2. Vnější třídění

U algoritmů s vnějším tříděním jsou tříděné prvky uloženy v externí paměti, odkud jsou po částech převáděni do paměti vnitřní, kde nad nimi proběhne daná operace. Poté jsou data opět přesunuta zpět do paměti externí. Kvůli zápisu do vnitřní paměti a zpět do vnější je tento postup pomalejší, než u vnitřního třídění. Vnější třídění je vhodné pro velké objemy dat.

Vybrané algoritmy a jejich rozbor

Selection sort - třídění výběrem

Nestabilní algoritmus se složitostí O(n²). V porovnání s dalšími kvadratickými algoritmy je tento obecně rychlejší než Bubble sort, ale pomalejší než Insertion sort. Výhodou výběrového algoritmu je jeho konstantní paměťová složitost.

De facto řadíme pole prvků tak, že vezmeme největší / nejmenší prvek řady a dáme jej na začátek. Poté vezmeme opět největší / nejmenší ze zbytku pole a dáme jej na druhé místo všech atd.

PŘÍKLAD

Pole je zprvu nesetříděné - všech n prvků je neuspořádaných
Pole je rozdělené na dvě části, setříděná a nesetříděná
1. Zapamatujeme si index prvního prvku v nesetříděné části
2. Procházíme zbytek nesetříděného pole a každý prvek porovnáváme s prvkem na první pozici
3. Je-li srovnávaný prvek menší, jeho pozice se stane pozicí s indexem 0(nahradí původně zapamatovaný prvek) - nejmenší z těchto prvků se na onen index přesune
Po každém průběžném kroku zvětšujeme setříděnou část pole o 1 prvek (posuneme hranici mezi setříděnou a nesetříděnou částí doprava)
V okamžiku, kdy setříděná část obsahuje n - 1 prvků je pole sorted, neboť v unsorted části již zbývá jen největší prvek, který je také na své konečné pozici

Mějme řadu 7 1 2 8 4 5 3 9.

zapamatujeme si pozici čísla 7
srovnáme s 1
zapamatujeme si pozici prvku 1
srovnáváme s dalšími prvky 2 8 4 5 3 9
nejmenší je 1, ergo vyměníme za 7
zapamatovaná je pozice prvku 1
řada vypadá následovně: 1 | 7 2 8 4 5 3 9
zapamatujeme si pozici prvku 7
srovnáme s 2, prvek 2 je menší, tak si zapamatujeme jeho pozici
srovnáme se zbytkem pole
2 je nejmenší, máme zapamatovanou pozici a vyměníme tedy prvek 2 za 7
pole vypadá takto: 1 2 | 7 8 4 5 3 9
zapamatujeme si index prvku 7
porovnáme se zbytkem pole
v průběhu si zapamatujeme pozice menších prvků, tj. nejprve 4
porovnáváme dále, narazíme na prvek 3, protože je menší než zapamatovaná 4 a posléze porovnávaná 9, přesuneme jej na pozici 3 (index [2])
1 2 3 | 7 8 4 5 9
atd.

Insertion sort - třídění vkládáním

Algoritmus vkládání je stabilní algoritmus založený na principu porovnávání řazených prvků. Výhodou Insertion sort je, že u téměř setříděného pole se složitostí blíží k O(n). Dochází pouze k průchodu, nikoli samotným posunům. Pro řazení malých polí (cca do 10 prvků je Insertion sort rychlejší, než Quicksort).

PŘÍKLAD

Mějme 1 prvek, ten je triviálně seřazen
Vezměme následující prvek a zařaďme jej na správné místo v jichž seřazených prvcích (seřazená část pole se zvětší o 1)
Dokud pole obsahuje nesetříděné prvky GOTO: 2

Mějme řadu 7 1 2 8 4 5 3 9.

rozdělíme na 2 části: 7 | 1 2 8 4 5 3 9
prvek 1 z nesetříděné části uložíme do proměnné x
7 | • 2 8 4 5 3 9
srovnáme prvek 7 s var x
x < 7, 7 se posune doprava
• | 7 2 8 4 5 3 9
již není co srovnávat, uložíme var x na volnou pozici a posuneme hranici setříděné části doprava
1 7 | 2 8 4 5 3 9
uložíme první prvek nesetříděné části, tj. prvek 2 do var x
tím se uvolní místo
1 7 | • 8 4 5 3 9
srovnáme x < 7, 7 se posune doprava
1 • | 7 8 4 5 3 9
dále srovnáme var x s 1, jelikož 1 < x, uložíme na aktuální pozici hodnotu var x
1 2 | 7 8 4 5 3 9
posuneme opět hranici setříděné části doprava
1 2 7 | 8 4 5 3 9
uložíme první prvek nesetříděné části, ergo 8 do var x, tím uvolníme místo
srovnáme prvek 7 s var x, 7 < x, tedy vložíme var x zpět na stejnou pozici a posuneme opět hranici
1 2 7 8 | 4 5 3 9
vezmeme prvek 4 a uložíme jej do var x
uvolníme místo
1 2 7 8 | • 5 3 9
porovnáme s prvky vlevo, dokud jsou setříděné prvky > var x, posouváme dané prvky doprava a porovnáváme dál
1 2 7 • | 8 5 3 9
1 2 • 7 | 8 5 3 9
prvek 2 < než hodnota var x, tedy uložíme na pozici [3] var x a posuneme opět hranici setříděné části doprava
1 2 3 7 8 | 5 3 9
atd.

Bubble sort - třídění výměnou

Jedná se o jednoduchý stabilní třídící algoritmus s kvadratickou asymptotickou složitostí, jehož vylepšená varianta je tzv. shakesort, což je de facto oboustranný bubblesort.

Řazené prvky jsou jako bublinky, kdy lehčí bublinka (prvek s nižším číslem) probublá na konec pole. V rámci algoritmu srovnáváme 2 sousední prvky a pokud je lehčí prvek vlevo, tak je algoritmus prohodí. Tím se prvek s menší hodnotou dostane blíže k pravému konci řady.

Se stejnou logikou pokračujeme na dalším indexu. Pokud je napravo prvek "lehčí" (má menší hodnotu), tak jej algoritmus nechá být a postoupí na další index. Každou iterací se tímto způsobem dostane na konec pole (doprava) ta nejlehčí bublinka.

Samozřejmě podmínka může být i obráceně a řadíme naopak vzestupně.

Po n-1 průchodech je pole seřazeno.

PŘÍKLAD (vzestupné řazení)

mějme řadu 7 1 2 8 4 5 3 9
postupně srovnáváme sousední prvky
7 > 1 - prohazujeme
1 7 2 8 4 5 3 9
7 > 2 - prohazujeme
1 2 7 8 4 5 3 9
7 < 8 - necháváme
1 2 7 8 4 5 3 9
8 > 4 - prohazujeme
1 2 7 4 8 5 3 9
8 > 5 - prohazujeme
1 2 7 4 5 8 3 9
8 > 3 - prohazujeme
1 2 7 4 5 3 8 9
8 < 9 - necháváme a pouštíme další průchod (řadíme již jen 7 prvků)
1 < 2 - necháváme
2 < 7 - necháváme
7 > 4 - prohazujeme
1 2 4 7 5 3 8 | 9
7 > 5 - prohazujeme
1 2 4 5 7 3 8 | 9
7 > 3 - prohazujeme
1 2 4 5 3 7 8 | 9
7 < 8 - necháváme
další průchod (řadíme již jen 6 prvků)
1 < 2 - necháváme
2 < 4 - necháváme
4 < 5 - necháváme
5 > 3 - prohazujeme
1 2 4 3 5 7 | 8 9
ostatní je okay - další průchod (řadíme již jen 5 prvků)
1 < 2 - necháváme
2 < 4 - necháváme
4 > 3 - prohazujeme
1 2 3 4 5 | 7 8 9
zbytek je okay - další průchod již není potřeba

Quicksort - rychlé třídění výměnou

Jedná se o nestabilní algoritmus s kvadratickou složitostí. Ačkoli zvolíme-li dobrého pivota (počáteční prvek), zrychlí se algoritmus na O(n * log n) očekávanou složitost. Tento algoritmus vymyslel v roce 1962 Sir Charles Hoare.

Principem algoritmu je zvolit počáteční prvek (pivot) a porovnáváme jej s každým prvkem. Menší prvky řadíme na jednu stranu od pivota a větší prvky na druhou stranu. Postup opakujeme por obě části, již bez pivota, neboť ten je umístěn na správném místě po prvním průchodu.

Pro řazení malých polí není Quicksort ideální, protože nemusí dojít k dobrému rozdělení pole na ideální poloviny. Lepší je jej použít na třídění velkého pole.

Strategie volby pivota Volba prvního či posledního prvku pole není ideální, neboť dojde k nedobrému dělení pole a nárůstu složitosti. Lepší je volit medián prvního, prostředního a posledního prvku řazeného úseku pole.

Druhou možnou strategií je výběr náhodného prvku. V praxi fungují pseudonáhodné RNG.

PŘÍKLAD - řazení vzestupně

mějme řadu 7 1 9 5 4 8 3 2
na začátku si zvolíme první prvek, naše řada má sudý počet prvků, ergo bereme prvek s nižším indexem z prvků 5 a 4
pro určení indexu daného prvku můžeme využít též vzorec: \[s = \frac{k + l}{2}\] kde $k$ je počáteční index tříděného úseku a $l$ je konečný index tříděného úseku
pivotem je prvek 5
nyní pracujeme s indexy i a j
i = 0, j = 7
řadíme menší ku pivotu doleva, větší ku pivotu doprava
po hledání pole
7 1 9 5 4 8 3 2
prvky vyměníme
2 1 9 5 4 8 3 7
máme nové indexy i = 1, j = 6
1 je vpravo správně, ergo posouváme index
i = 2, j = 6
2 1 9 5 4 8 3 7
3 < 9, prvky prohodíme -> 3 je menší než 5 a má být nalevo
2 1 3 5 4 8 9 7
nové indexy i = 2, j = 5
prvek 3 okay, 8 okay
nové indexy i = 3, j = 4
2 1 3 5 4 8 9 7
vyměníme, neboť 4 má být od pivota (5) nalevo
2 1 3 4 5 8 9 7
poté co se pivot posunul, se změnili indexy (i > j)
i = 4 (zleva), j = 3 (zprava) tím třídící krok končí a pole se dělí na dvě části
2 1 3 4 | 5 8 9 7
nyní každou část třídíme zvlášť (A | B)
určíme pivoty, pro A 1, pro B 8
2 1 3 4
i = 0, j = 3
kroky hledání 2 není okay, 4 je okay
i = 0, j = 2
2 není okay, 3 je okay
i = 0, j = 1
2 1 3 4
prvky vyměníme, aby vetší od pivota bylo vpravo
1 2 3 4
posuneme indexy i = 1, j = 0, (i > j) ukončí se krok a rozdělí pole
1 | 2 3 4
levá část má jeden prvek a považuje se tudíž za seřazenou
pravá část 2 3 4
pivot je 3
i = 1, j = 3 (indexace bere stále v potaz první prvek 1)
2 je okay, 4 je okay
i = 2, j = 2
prvek změní sebe sama (3 za 3)
2 3 4
i = 3, j = 1 (i > j) končí krok
rozdělené pole A je 2 | 3 | 4
všechny části mají jeden prvek a jsou brány za seřazené
část A je dokončena, zbývá část B
5 8 9 7
i = 4, j = 7
pivotem je prvek 8
5 je okay, 7 není okay
i = 5, j = 7
5 8 9 7
prvky se prohodí
5 7 9 8
i = 6, j = 6
9 se prohodí za sebe sama
i = 7, j = 5 (i > j), končí krok, rozdělí se pole
5 7 | 9 8
5 a 7 je okay respektive i = 4, j = 5
pivot je 5, 7 je okay, i = 5, j = 4, rozdělí se pole
5 | 7 -> jsou seřazeny
9 a 8, i = 6, j = 7, pivot je 9
čísla se prohodí a změní se indexy, i = 7, j = 6 -> rozdělí se pole
8 | 9
tím pádem máme 5 | 7 | 8 | 9
část B je rovněž srovnána
celé pole: 1 2 3 4 5 7 8 9

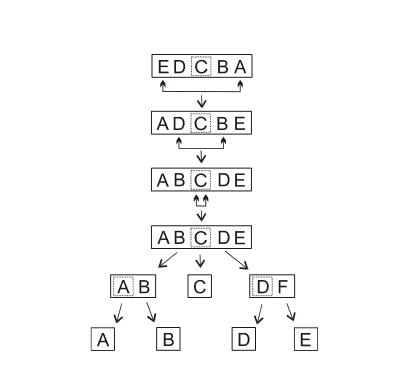
Níže je zachycen ještě jiný postup setřídění pěti písmen s určeným pivotem uprostřed.


obr. 1: Příklad Quicksort - Pivot je prvek "C"
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

Heapsort - třídění haldou

Třídění haldou je v podstatě nejefektivnější algoritmus se složitostí O(n * log n). Tato složitost je zaručená, díky tomu je Heapsort ideální pro použití v real-time systémech.

Halda je specifický typ binárního stromu, v jehož každém uzlu je jeden tříděný prvek. Vlastností těchto prvků je, že prvek v otcovském uzlu má větší hodnotu než prvky uložené v jeho následnících. Ideálním binárním stromem je tzv. vyvážený binární strom, který má všechny vrstvy zaplněné, až na vrstvu poslední, jež jako jediná může být neúplná.


obr. 2: Heapsort - uzly
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

Vrstvou binárního stromu rozumíme množinu uzlů, jež leží na stejné vodorovné úrovni, tedy mají stejnou vzdálenost od kořene. Poslední vrstva je označena jako $h$, což označuje také výšku haldy. Směrem nahoru se výška logicky snižuje, tedy: $h - 1, h - 2 $ apod.

Uzly v dané vrstvě $k$ se označují $2^k, 2^{k+1}$... Následnicí v uzlu s indexem $i$ se značí $2 * i + 1$ a $2 * i + 2$, ergo následníci uzlu $u_i$ jsou $u_{2 * i + 1}$ a $u_{2 * i + 2}$.

Výšku haldy zjistíme prostřednictvím vzorce:

\[h = log_2(n)\]

kde $n$ je počet prvků haldy a $h$ je zmiňovaná výška.

Následně, zaplníme binární strom tříděnými prvky a budeme odspoda procházet jednotlivé nelistové uzly. Uzly procházíme v pořadí:

$u_{\frac{n}{2}-1}$, $u_{\frac{n}{2}-2}$,...., $u_1$, $u_2$

Bude-li hodnota v nelistovém uzlu menší, než hodnota v jeho následníku, prvky prohodíme. Pokračujeme k dalšímu nelistovému uzlu atd. Takto prvky vyměníme tak, aby každý uzel splňoval vlastnost haldy. tj:

Prvek v následníkovi je menší, než prvek v rodičovském uzlu.

V kořenu haldy ve finále musí být největší prvek. Ten vyměníme s prvkem v posledním uzlu haldy a strom o tento list zkrátíme. Takto zkracujeme a měníme prvky, než nám zůstane pouze jeden uzel.

Ukážeme si to na následujícím příkladu. Snazší je podívat se na video :-D

De facto jde o tři věci:

Urovnat haldu do MaxHeap - postupu se říká "heapify"
Vyměnit prvek v kořenu za prvek v posledním listu
Tento list odstranit

mějme nesetříděnou řadu prvků: 7 2 8 1 5 3 9 4
$n = 8$ a $log_2(8) = 3$, tedy počet úrovní je 3
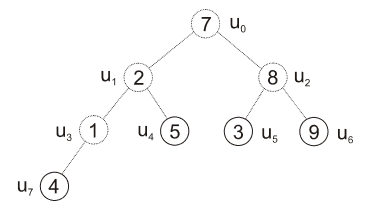
indexujeme od 0 a jednotlivé uzly řadíme odshora dolů a zleva doprava


obr. 3: Heapsort - tvorba stromu
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

vezmeme poslední z nelistových uzlů $u_3$ a porovnáme jeho hodnotu s následníkem, $1 < 4$, ergo prohodíme prvky
další nelistový uzel na řadě je $u_2$, větší hodnotu má list $u_6$, vyměníme tyto prvky
následuje $u_1$ a výměna s jeho největším následníkem $u_4$


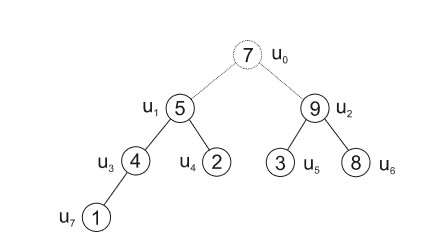obr. 4: Heapsort - výměna prvků v uzlech $u_3, u_2, u_1$
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

zbývá již jen uzel $u_0$, vyměníme jeho prvek s prvkem v uzlu $u_2$


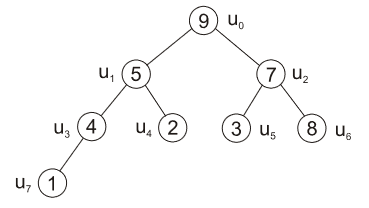obr. 5: Heapsort - výměna prvků v uzlech $u_0$
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

po těchto výměnách nám stále nesplňuje podmínky haldy uzel $u_2$
musíme vyměnit prvky mezi $u_2$ a $u_6$


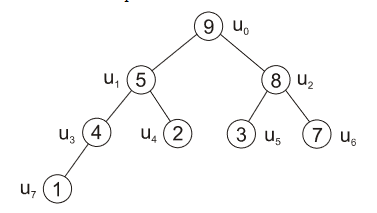obr. 6: Heapsort - výměna prvků v uzlech $u_2, u_6$ - hotový strom
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

Nyní můžeme začít třídit :-D

vyměníme prvek kořene s posledním listem a tento list odebereme
zustane nám 7 prvků: 1 5 8 4 2 3 7


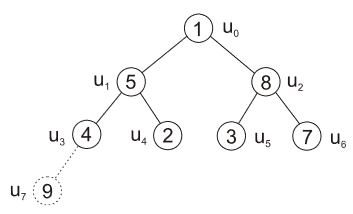obr. 7: Heapsort - odebrání listu $u_7$
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

teď je třeba opět strom upravit, tedy prohodit prvky v uzlech $u_0, u_2, u_6$
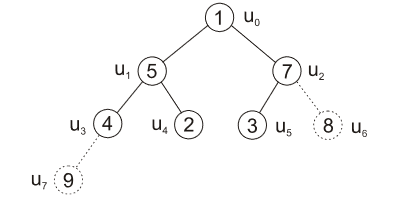
následně vyměnit prvek v kořenu opět za prvek v posledním listu a tento list odebrat


obr. 8: Heapsort - odebrání listu $u_6$ po předchozí výměně
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

další uzly nesplňují podmínky haldy, tedy je nutné vyměnit prvky mezi uzly $u_0$ a $u_2$ a poté $u_2$ a $u_5$


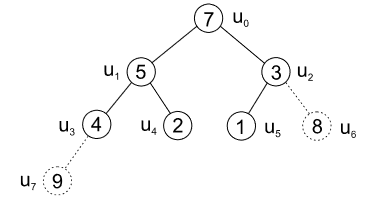obr. 9: Heapsort - výměna prvků před odebráním listu $u_5$
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

prohodíme prvky 7 a 1 a odebereme list $u_5$
opět prohodíme prvky v $u_0 a u_1, u_3 a u_1$


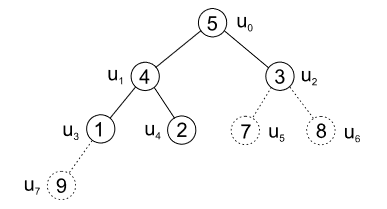obr. 10: Heapsort - výměna prvků před odebráním listu $u_4$
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

prohodíme prvky v $u_0$ a $u_4$ a list $u_4$ dáme pryč


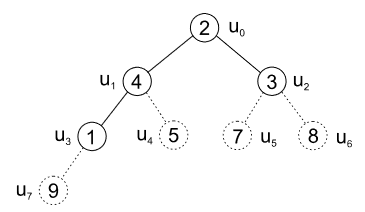obr. 11: Heapsort - odebrání listu $u_4$
zdroj: https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf

vyměníme prvky v $u_0$ za $u_1$
poté kořen s posledním listem $u_3$ a list dáme pryč
poté prohodíme prvek v $u_2$ za prvek v kořenu, abychom udrželi podmínky haldy
vyměníme prvek v kořenu za prvek v posledním listu a ten dáme pryč ($u_2$)
zbývají dva prvky, musíme je opět prohodit, abychom utvořili haldu
poté setřídíme, takže vyměníme zpět a odebereme poslední list $u_1$
zbude nám jeden prvek
MÁME SETŘÍDĚNO!


obr. 12: Heapsort - zbytek postupu

ZDROJE

(SKRIPTA) https://phoenix.inf.upol.cz/esf/ucebni/zakladni_alg.pdf
(VIDEO YT) https://www.youtube.com/watch?v=2DmK_H7IdTo
(WEB) https://www.algoritmy.net/

Binární vyhledávací stromy

definice, užití a implementace, vyvažování, AVL stromy – princip algoritmu

Definice

Binární vyhledávací strom je datová struktura založená na binárním stromu, v němž jsou jednotlivé prvky uspořádány tak, aby v tomto stromu bylo možné rychle vyhledávat.

Binární strom

Jedná se o orientovaný graf s jedním vrcholem (kořen stromu), z něhož vede cesta ke všem ostatním vrcholům. Každý vrchol může mít maximálně dva potomky. Každý potomek může mít maximálně jednoho předka (s vyjimkou kořene, ten nemá žádného předka).


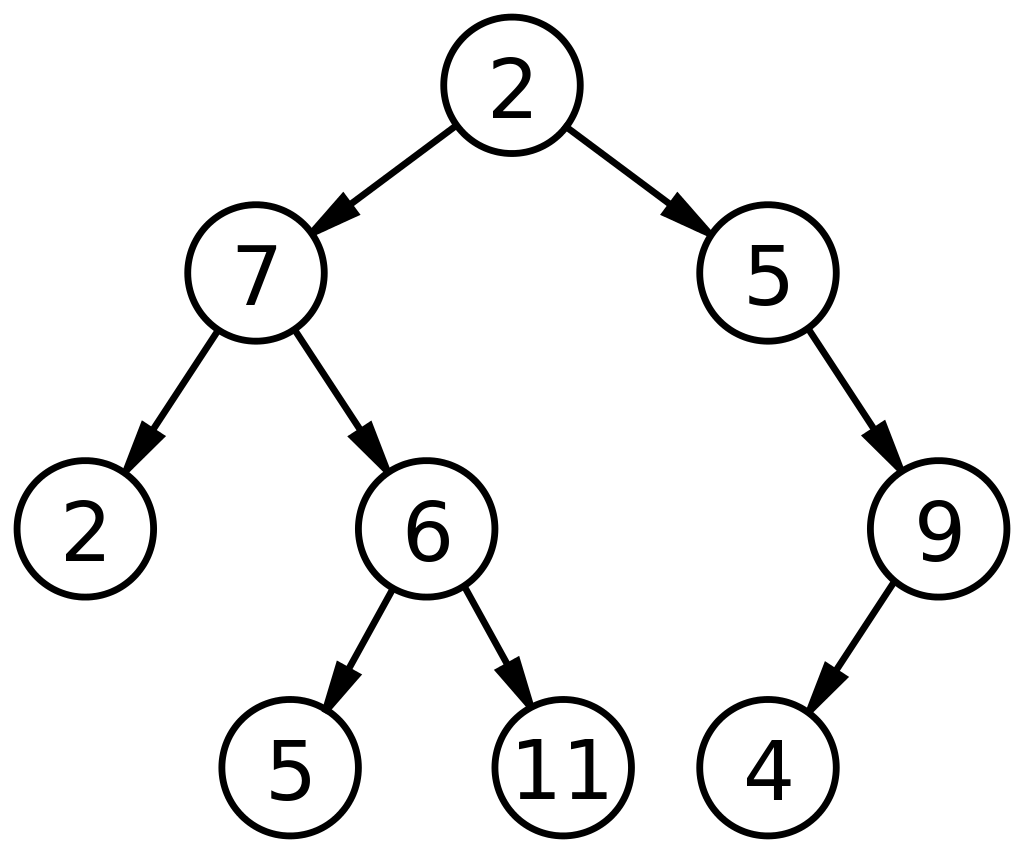obr. 1: Binární strom
Převzato z: https://cs.wikipedia.org/wiki/Bin%C3%A1rn%C3%AD_strom

Implementace a vlastnosti vyhledávacích binárních stromů

jedná se o binární strom (každý uzel má nejvýše dva potomky)
každému uzlu je přiřazen určitý klíč (hodnota)
levý podstrom každého uzlu obsahuje pouze menší hodnoty než je klíč tohoto uzlu
pravý podstrom každého uzlu obsahuje pouze větší hodnoty než je klíč tohoto uzlu

Užití

konstrukce a prohledávání asociativních polí (klíč - hodnota)
- průchod je pomalejší nežli hashovací tabulka, ale průchod stromem vydá seznam seřazených hodnot (hodí se na intervalové dotazy)
slouží jako základ pro komplexnější vyhledávací datové struktury

Operace

Máme základní čtyři:

vyhledávání
vkládání
mazání
procházení stromu

Vyhledávání

Probíhá rekurzivně. Začínáme v kořenu stromu. Algoritmus porovná hledanou hodnotu s klíčem uzlu. Pokud se rovná, našli jsme hledanou hodnotu. Pokud je menší, jdeme doleva, pokud je větší, jdeme doprava. Toto se děje, dokud jsme nenalezli hodnotu, nebo nedorazili do listu stromu.

Časová složitost vyhledávání závisí na hloubce stromu. V průměrném případě má logaritmickou časovou složitost O(log n), ale pokud je strom nevyvážený a podobá se seznamu, může mít i lineární časovou složitost O(n). Otázka správného vyvážení je z tohoto pohledu kritická a řeší ji například AVL-strom.

Vkládání

Probíhá podobně jako vyhledávání, akorát hledanou hodnotou je hodnota vkládaného uzlu. Mohou nastat dva případy:

strom již hodnotu obsahuje, není třeba ji vložit
algoritmus narazil na neexistující uzel (například chce jít z uzlu doprava, ale žádný uzel tam není) -> našli jsme místo, kam uzel patří

Mazání

Zde může nastat několik případů:

hledaným uzlem je list, ten můžeme klidně smazat
hledaným uzlem je uzel s jedním potomkem -> smažeme uzel a nahradíme tento uzel potomkem
hledaný uzlem je uzel se dvěma potomky -> hodnota uzlu je nahrazena nejbližší vyšší (nejlevější uzel pravého podstromu), nebo nižší hodnotou (nejpravější uzel levého podstromu)

Procházení stromu

Pouze procházíme strom, nijak ho neměníme, složitost odpovídá výšce stromu.

Řazení uzlů

Jedná se o proces zařazení hodnot stromu dle velikosti.

Vkládáme všechny hodnoty které chceme seřadit do vhodně uspořádané datové struktury -> binární strom. Následně stromem projdeme do hloubky a získáme seznam hodnot uspořádaný podle velikosti.

nejhorší případ je n² času, a to pokud se přidávají již seřazené hodnoty. Ty se totiž spojí do seznamu takže strom nemá levé větve.

Metody vkládání a mazání jsou často destruktivní -> tedy ničí vyváženost našeho stromu (to je takový strom, kde je rozdíl výšky podstromů uzlu menší než 2).

Jak vyvážíme strom?

AVL stromy

Jedná se o typ binárního vyhledávacího stromu. Konkrétně se jedná o samovyvažující se binární vyhledávací strom.

K vlastnostem binárních vyhledávacích stromů přidává AVL další vlastnost:

délka nejdelší větve levého a pravého podstromu každého uzlu se liší nejvýše o 1, jinak strom není vyvážený

AVL strom definuje postupy zajišťující vyvážení stromu pro operace, jež mají šanci strom zdegenerovat:

vkládání
mazání

Vše je založeno na kritériu vyváženosti. Jedná se o číslo, které nám říká, jak se liší výška levého a pravého podstromu daného uzlu. Každý uzel má ideálně svoje kritérium vyváženosti, které pravidelně aktualizujeme.

Vkládání do AVL stromu

Stejné jako u binárního vyhledávacího stromu, až na to, že po vložení se aktualizují koeficienty vyváženosti uzlů, které byly na cestě směrem ke kořenu.

Není-li splněno kritérium vyváženosti, musíme provést vyvažování stromu pomocí cyklické záměny ukazatelů (rotace stromu).

Při vkládání stačí vyvážit pouze první nalezený uzel, jehož koeficient vyváženosti je porušen, tím že ho opravíme, vyvážíme celý strom -> změna vyvolaná přidáním uzlu ovlivní pouze první nevyvážený uzel a jeho podstromy.

Mazání z AVL stromu

Stejné jako u binárního vyhledávacího stromu tím, že pokud dojde k porušení vyváženosti, provede se vyvážení. Na rozdíl od vyvažování při vkládání uzlů, při odebírání uzlů se musí projít celá cesta až do kořene stromu a opravit koeficienty vyvážení a případně provést rotace -> změna vyvolaná odstraněním může ovlivnit vyváženost celého podstromu kořene.

Vyvažování

Vyvážení docílíme tím, že vhodně zrotujeme celý podstrom, tak aby byla splněna vlastnost AVL stromů (Výška dvou podstromů se může lišit maximálně o 1)

rotací změníme pořadí uzlů ve stromu; máme dva druhy rotace:
- jednoduchá (rotujeme doleva, pokud je pravý podstrom vyšší; rotujeme doprava pokud je levý podstrom vyšší)
- složitá (rotujeme dvakrát pokaždé v opačném směru)
rotace probíhají vždy skrze uzel, jehož koeficient vyváženosti je narušen
rotace si můžeme představit jako řetěz, za který zatáhneme a levý/pravý podstrom posuneme


obr. 2: Příklad pravé rotace. T označuje podstromy, x a y jsou uzly.
Převzato z: https://akela.mendelu.cz/~foltynek/TI/old/TI13%20Stromy.pdf

Zdroje

Binární vyhledávací strom. Wikipedie: Otevřená Encyklopedie. [online] @2023 [citováno: 17.05.2023]
Dostupné z: https://cs.wikipedia.org/wiki/Bin%C3%A1rn%C3%AD_vyhled%C3%A1vac%C3%AD_strom
Binární strom. Wikipedie: Otevřená Encyklopedie. [online] @2023 [citováno: 17.05.2023]
Dostupné z: https://cs.wikipedia.org/wiki/Bin%C3%A1rn%C3%AD_strom
Stromy. Mendelova univerzita v Brně. [online] @2023 [citováno: 17.05.2023]
Dostupné z: https://akela.mendelu.cz/~foltynek/TI/old/TI13%20Stromy.pdf
AVL-strom. Wikipedie: Otevřená Encyklopedie. [online] @2023 [citováno: 17.05.2023]
Dostupné z: https://cs.wikipedia.org/wiki/AVL-strom

Vícecestné stromy

vícecestné stromy, 2-3-4 stromy, 2-3 stromy, B stromy, B+ stromy, popis, použití

Tato otázka navazuje na otázku binární vyhledávací stromy.

vícecestné stromy se liší tím, že každý uzel může mít více než dva potomky
jedná se o samovyvažující se stromy, stejně jako v případě AVL stromů
řeší problém ukládání velkého množství dat -> čím hlubší strom, tím delší doba k provedení operace
- vícecestné stromy mohou mít více potomků pro jeden uzel
- každý uzel může v sobě mít uložených více hodnot

B stromy

Těmto stromům se budeme věnovat nejpodrobněji, neboť jsou generalizací (obecným případem vícecestného stromu), ze kterého vycházejí i všechny ostatní.

Jedná se o vícecestné stromy, kde každý uzel může mít n potomků a v každém uzlu může být uloženo n-1 hodnot nebo klíčů.

pokud má uzel 4 potomky, tak tento uzel v sobě může mít uložené 3 hodnoty
každý uzel může mít jinou, řekněme velikost (počet v něm uložených hodnot)
stále platí, že menší hodnoty jdou doprava a větší doleva, proto n-1
podívejte se na obrázek pod a pokuste se s touto logikou přidat čtvrtého potomka, nepůjde to


obr. 1: Příklad B stromu, uzel má `3` hodnoty a tím pádem `4` potomky
převzato z: https://www.youtube.com/watch?v=SI6E4Ma2ddg

Abychom mohli strom označit za B strom, tak musí splňovat 3 podmínky:

každý uzel, musí mít minimálně m/2 potomků, kde m je hloubka stromu (toto neplatí pro listy)
- pravidlo nám zaručuje, že všechny vnitřní uzly jsou vždy alespoň poloplné
- můžeme tedy dva uzly spojit v jeden celý uzel, nebo celý uzel rozdělit na dva poloplné
  - hodí se při operacích mazání a vkládání
každý uzel může mít n potomků a v každém uzlu může být uloženo n-1 hodnot nebo klíčů (viz výše)
všechny listy musí být na stejném patře

Shrnutí:

každý B strom má svoji výšku (počet pater, značíme m, jedná se výšku celého stromu)
každý uzel obsahuje n hodnot
uzel musí mít minimálně m/2 potomků a maximálně n-1 potomků (s vyjimkou listů)
všechny listy se musejí nacházet na stejné úrovni


obr. 2: Příklad B stromu, vnitřní uzly splňují požadavek na počet potomků
převzato z: https://www.youtube.com/watch?v=SI6E4Ma2ddg

Operace nad B stromem (vkládání, mazání)

Vícecestné stromy umožňují stejné operace, jako binární vyhledávací stromy. Liší se procesem vyvažování.

Operace vkládání

vložíme prvek na jeho místo
zkontrolujme, zdali jsme nepřekročili limit uzlu (o limitu uzlu se dozvíme na konci kapitoly)
pokud ano, rozdělíme rovnoměrně uzel, kam jsme prvek přidali na 2 (na dva různé uzly)
vezmeme jeden z původních prvků nového uzlu a přidáme ho do rodičovského uzlu
zkontrolujeme rodičovský uzel zdali jsme nepřekročili limit uzlu
pokud ano, opakujeme postup

Operace mazání

nalezneme prvek a smažeme ho
pokud dostaneme nevyvážený strom, řešením jsou rotace stejné jako binárních vyhledávacích stromů s tím rozdílem, že se podíváme na sousední listy a vybereme ten, který má dostatečné množství prvků (smazání prvku neporuší vlastnosti)
- provedeme rotaci -> kořen posuneme na místo smazaného prvku a nyní prázdný kořen nahradíme nejvyšším prvkem tohoto listu, pokud se jedná o levého souseda (pravá rotace)
- pokud se jedná o pravého souseda, kořen posuneme na místo smazaného prvku a nyní prázdný kořen nahradíme nejnižším prvkem souseda (levá rotace)
pokud je porušena podmínka minimálního počtu potomků tak vezmeme nejvyšší hodnotu z rodiče, nahradíme touto hodnotou smazanou hodnotu a spojíme levé listy tohoto rodiče do jednoho
pokud mažeme rodiče, tak nahradíme mazanou hodnotu nejvyšší hodnotu levého potomka, nebo nejnižší hodnotou pravého potomka (volba je na nás)
- nyní je dosti velká šance, že dostaneme nevyvážený strom -> rotujeme jako v 1. bodě

Shrnutí:

Proces mazání se liší podle toho, z jakého uzlu prvek mažeme:

list
rodič

Po smazání kontrolujeme zdali strom splňuje vlastnosti B stromu a na základě toho volíme vhodný postup, tak aby tyto vlastnosti byly zachovány.

rotace neprovádíme s celými uzly, ale s prvky uzlů

Vyhledávání ve stromu

Stejný jako v případě binární vyhledávací stromů.

Průchod stromem

Provádí se průchod do šířky nebo také in-order.

začínáme na levé straně u potomka kořene (jdeme prvek po prvku)
pokud narazíme na potomka, uzlu, prohledáme ho
pokud dorazíme na konec uzlu, vracíme se do rodiče
prohledávání končí, jakmile jsme prohledali poslední prvek nejvíce pravého uzlu

Krásné, 12 minutové video ohledné B stromů lze nalézt zde.

Co je to limit prvků uzlu?

Jak již bylo řečeno, B stromy jsou generickým případem. Co se týče limitů tak víme že:

uzel může mít tolik potomků, kolik je počet jeho prvků - 1
uzel může mít minimálně tolik prvků, kolik je hloubka stromu/2
jaký je ale maximální počet (limit) prvků uzlu?

2-3 a 2-3-4 stromy

Jedná se o b stromy, kde mohou mít uzly:

minimálně 2 a a maximálně 3 prvky v případě 2-3 stromu
minimálně 2 a maximálně 4 prvky v případě 2-3-4 stromu
strom s minimálně 2 prvky a maximálně 5 prvky by byl 2-3-4-5 strom

B+ stromy

B+ stromy jsou variací B stromů ve které jsou všechny hodnoty (tedy i hodnoty ne-listových uzlů) uložené v listech.


obr. 3: Příklad B+ stromu, listy obsahují všechny hodnoty
převzato z: https://www.youtube.com/watch?v=49P_GDeMDRo&list=PLsEFMZUL5KsOqKHhxquVleVkM9LFLFSo0

sousedi stejného rodiče se nazývají sourozenci
sousedi jiného rodiče (stejná úroveň, ale jiný rodič) se nazývají bratranci
maximální počet potomků uzlů je stejný jako v případě B stromů (o jednoho více než je počet prvků v uzlu)
minimální počet je také stejný jako v případě B stromů (maximální počet/2) -> vztahuje se i na listy
hodnoty v listech jsou seřazené podle pořadí od nejnižší po nejvyšší

Operace

Vkládání

prvek přidáváme do listu na jeho místo
pokud je list plný, tak se pokusíme přesunout nejvyšší prvek do sourozence vlevo, pokud to nejde tak nejnižší prvek do sourozence vlevo -> prostě do jiného sourozence
pokud žádné sourozence nemáme, tak rozdělíme list na dvě části a vytvoříme nový list, který obsahuje polovinu vyšších hodnot (list tedy půjde vpravo)
- pokud máme lichý počet prvků, vezmeme n+1 prvků z původního listu
hodnota v rodiči vždy udává minimum daného listu - aktualizujeme tedy hodnotu v rodiči
pokud dostáváme větší počet listů, než je povoleno (narušíme vlastnosti B stromů), tak se podíváme na levého sourozence tohoto uzlu a pokud má místo, předáme mu nejvíce levý (nejnižší list)
- je také možné podívat se na pravého sourozence a předat mu nejvíce pravý (nejvyšší list)
- pokud místo nemá, provedeme předchozí kroky a rodičovský uzel rozdělíme na dva, přičemž každý má pod sebou patřičné listy

Mazání

zkontrolujeme, zdali má uzel minimální počet hodnot, pokud ano, je vše v pořádku
pokusíme se vzít si maximální hodnotu od levého sourozence
pokud to nejde (máme plno nebo ho nemáme), spojíme uzel s levým sourozencem -> přesuneme do něj všechny hodnoty
pokud ho nemá, nebo je sourozenec plný, pokusíme se vzít si minimální hodnotu od pravého sourozence
- toto se stane pouze u uzlů, které nemají levého sourozence
pokud to nejde, spojíme uzel s pravým sourozencem

Příklad ohledně mazání prvků je uveden zde.

Já osobně bych se raději popisu operací vyhnul.

Využití vícecestných stromů

Využití klasických B stromů (2-3,2-3-4...):

v oblasti slovníků
oblasti externích disků, kde velikost uzlu/listu je stejně velká, jako velikost čteného bloku (indexace bloku)

Využití B+ stromů:

při indexování velkého množství dat, které se nevejdou do RAM, například záznamů v tabulkových databázích
- strom je uložen v RAM (kromě listů)
- listy stromu, jsou uložené na disku

Zdroje

B-Trees Made Simple | Introduction to B-Trees | B-Tree Operations | Geekific. Geekific. [online] @2021 [citováno: 22.05.2023]
Dostupné z: https://www.youtube.com/watch?v=SI6E4Ma2ddg
2–3–4 tree. Wikipedia: The Free Encyclopedia. [online] @2023 [citováno: 22.05.2023]
Dostupné z: https://en.wikipedia.org/wiki/2%E2%80%933%E2%80%934_tree
B+ Tree Basics. Stephan Burroughs. [online] @2016 [citováno: 22.05.2023]
Dostupné z: https://www.youtube.com/watch?v=49P_GDeMDRo&list=PLsEFMZUL5KsOqKHhxquVleVkM9LFLFSo0&index=1
https://www.youtube.com/watch?v=h6Mw7_S4ai0&list=PLsEFMZUL5KsOqKHhxquVleVkM9LFLFSo0&index=2
https://www.youtube.com/watch?v=QrbaQDSuxIM&list=PLsEFMZUL5KsOqKHhxquVleVkM9LFLFSo0&index=3

Hašovací tabulky

Základní pojmy z teorie grafů

graf, rozdělení a typy grafů, vážený graf, podgraf, cesta, kružnice, strom, kostra grafu, různé reprezentace grafu a jejich výhody a nevýhody

Definice grafu

Graf je množina objektů, mezi kterými existuje určitá vazba, která tyto objekty spojuje.

Tato množina objektů je uspořádaná trojice (U,H,F), kde U je množina uzlů, H je množina hran a f: H -> U²

Vlastnosti grafu

Neorientovaný graf: V základu je každý graf orientovaný, jestliže hrany jsou uspořádané dvojice. Hrany neuspořádaného grafu jsou dvouprvkové množiny. Hrany orientovaného grafu mají tedy pevně danou orientaci. Pokud máme orientovaný graf, lze k němu sestrojit graf neorientovaný tím, že z orientovaného grafu odstraníme informaci o směru hran.
Prostý graf: Prostý graf je takový graf, jenž neobsahuje žádnou rovnoběžnou hranu.
- graf obsahuje rovnoběžnou hranu, pokud existují dvě hrany, které propojují dva totožné uzly
Prázdný a nekonečný graf: Prázdná a nekonečné množina uzlů U.
Diskrétní a úplný graf: Diskrétní graf je takový graf, v němž žádné dva uzly nejsou spojené hranou. Úplný graf je takový neorientovaný graf v němž jsou každé dva různé uzly spojené hranou.
Biparitní graf: Takový graf, jehož množinu uzlů je možné rozdělit na dvě disjunktní (naprosto odlišné) množiny tak, že žádné dva vrcholy ze stejné množiny nejsou spojeny hranou.
Regulární graf: Takový graf, jehož všechny uzly mají stejný stupeň. Stupeň uzlu je hodnota, označující počet hran tohoto uzlu.
Podgraf: Část grafu, pokud obsahuje všechny uzly jedná se o faktor.
Sled: Posloupnost hran, které na sebe navazují, se nazývá sled. Pokud se žádná hrana neopakuje, jedná se o tah. Tah, ve kterém se neopakuje žádný vrchol se nazývá cesta.
Kružnice a cyklus: Uzavřená cesta v neorientovaném a orientovaném grafu
Souvislý graf: Mezi každými dvěma uzly existuje sled. Každý maximální souvislý podgraf je komponenta
Uzlové a hranové řezy: množina uzlů / hran jejichž odstraněním se zvýší počet komponent Uzlový řez s jedním uzlem je artikulace (Množina obsahuje jeden uzel, jehož odstraněním vytvoříme jednu či více komponent). Hranový řez s jednou hranou je most (Množina obsahuje jednu hranu, kterou když odstraníme, vytvoříme jednu či více komponent).
Komponenta : Samostatná část grafu, která není spojená s dalšími částmi grafu.
Klika a nezávislá množina: Klika je úplný podgraf, nezávislá množina je diskrétní podgraf.

Charakteristiky uzlů

Uzly: následníci, předchůdci, sousedi uzlu
- Následníci a předchůdci : Lze určit u stromu.
- Sousedi uzlu: Uzly, jež jsou spojeny s uzlem skrze hrany, se nazývají sousedi.
Hrany: výstupní okolí, vstupní okolí, okolí uzlu
- Výstupní okolí : Hrany, jež vystupují z uzlu
- Vstupní okolí : Hrany jež vstupují do uzlu
- Okolí uzlu : Množina hran, jež vstupuje/vystupuje z uzlu. U neorientovaného grafu můžeme určit pouze okolí uzlu.
Stupně: výstupní stupeň, vstupní stupeň, stupeň uzlu
- Výstupní stupeň : Počet výstupních hran směřujících od uzlu
- Vstupní stupeň : Počet vstupních hran směřujících do uzlu
- Stupeň uzlu : Počet hran patřících k uzlu. U neorientovaného grafu lze uzlu určit pouze tento stupeň (Chybí informace o směru hran).

Ohodnocené grafy

Uzlové ohodnocení grafu

Zobrazení $k: U > R$, nazývá se klíč a dá se využít při řazení, vyhledávání či kódování.

Hranové ohodnocení grafu

Zobrazení $d: H > R$, každá hrana má k sobě přiřazenou hodnotu (váhu).

Strom

Jedná se o souvislý graf, který neobsahuje žádnou kružnici. Základem stromu je uzel, pojmenovaný kořen (root). Bezprostředně následující uzel ve směru z kořene do uzlu se nazývá „dítě“ nebo „syn“ uzlu (anglicky child); uzel bezprostředně předcházející je „rodič“ uzlu (anglicky parent). Kořen stromu nemá rodiče a list stromu nemá žádné syny. Ostatní uzly mohou mít libovolný počet synů.

Kostra grafu

Kostrou grafu budeme rozumět libovolný podgraf, který hranami spojuje všechny vrcholy původního grafu a zároveň sám neobsahuje žádnou kružnici (→ jde o strom).

Minimální kostra

Úloha hledání minimální kostry nám popisuje, jak máme spojit všechny vrcholy grafu "co nejlevněji" - hranami s nejnižší váhou (ohodnocením). Praktickým využitím mohou být například rozvody elektřiny mezi městy - jak propojit města co nejmenší délkou elektrického vedení.

Hledání minimální kostry

K tomuto účelu se používají algoritmy pro hledání kostry grafu. Jedná se o tzv. hladové algoritmy. Velmi používaným algoritmem je Kruskalův algoritmus. Pracuje na principu spojování hran s nejmenším ohodnocením, dokud tyto hrany nespojí vrcholy celého grafu.

Popis Kruskalova algoritmu

Všechny hrany si seřadíme podle velikosti (vzestupně - od hrany s nejmenší váhou).
Hranu s nejmenší váhou použijeme jako první hranu kostry.
Pokud jsme tím už vytvořili kostru (graf měl jen dva vrcholy), končíme. V opačném případě vezmeme hranu s druhou nejmenší váhou. POZOR! Pokud by nám v grafu vznikla kružnice, hranu nepoužijeme.
Opakujeme minulý krok, dokud vznikající kostra nespojí všechny vrcholy grafu.

Další algoritmy pro hledání minimální kostry

Borůvkův algoritmus

Funguje na principu skládání komponent. Na začátku jsou všechny uzly grafu považovány za samostatné komponenty. Algoritmus v každém svém kroku propojí každou komponentu s jinou komponentou pomocí nejkratší možné hrany. Jelikož Borůvkův algoritmus vyžaduje, aby měly všechny hrany unikátní váhu, tak při propojení komponent nikdy nemůže vzniknout cyklus.

Jarník-Primův algoritmus

Algoritmus vychází z libovolného uzlu a udržuje si seznam již objevených uzlů a jejich vzdáleností od propojené části grafu. V každém svém kroku připojí ten z uzlů, mezi nímž a propojenou částí grafu je hrana nejnižší délky a označí sousedy nově připojeného uzlu za objevené, případně zkrátí vzdálenosti od již známých uzlů, pokud byla nalezena výhodnější hrana. V okamžiku, kdy jsou propojeny všechny uzly, algoritmus terminuje.

Reprezentace grafů

Jedná se o způsob, kterým zobrazit graf.

Obrázkem

Grafická reprezentace grafu. (kolečkové uzly, čárky mezi nimi aneb hrany)

Výhody

Přehlednost pro lidské oko
Lze použít pro jakýkoliv typ grafu

Nevýhody

Pro zpracování za pomocí programu je nutné graf reprezentovat jinak
Velké grafy se stávají nepřehledné

Matice sousednosti

Zápis grafu pomocí matice.

Postup vytváření matice sousednosti
- Nejprve si všechny vrcholy očíslujeme.
- Za rozměr matice musíme zvolit počet vrcholů. Kdybychom měli například graf se 4 vrcholy ale matici rozměrů jen 3×3, nemohli bychom zapsat hrany vedoucí do/z čtvrtého vrcholu.
- Pokud vede mezi dvěma vrcholy hrana, zapíšeme do matice na pozici [číslo jednoho vrcholu, číslo druhého vrcholu] a na pozici [číslo druhého vrcholu, číslo prvního vrcholu] číslo 1. Jinak zapíšeme 0.

Výhody

Maticová reprezentace je vhodná pro programové zpracování
Lze použít pro orientovaný graf i neorientovaný graf (pro neorientovaný graf je matice symetrická, protože hodnota prvku na souřadnicích např. (1,2) je stejná jako hodnota prvku na pozici (2,1))

Nevýhody

Pro lidské oko nepřehledné

Existují i další druhy zápisů pomocí matice

Matice incidence : Řádky jsou uzly sloupce jsou hrany. V poli se nachází 1, pokud se jedná o výstupní hranu uzlu. 0 pokud hrana nepatří do okolí uzlu a 1 pokud se jedná o vstupní hranu uzlu.
Matice vzdáleností : Řádky i sloupce jsou uzly. Do pole se zapisuje vzdálenost mezi jednotlivými uzly. Získává se pomocí výpočtu minimální vzdálenosti mezi jednotlivými uzly.
Matice dostupnosti: Řádky i sloupce jsou uzly. V poli je 1, pokud existuje orientovaná cesta z uzlu A (sloupec) do uzlu B (řádek). Nelze použít pro neorientované grafy.

Seznam vrcholů se seznamem hran

Jedná se o seznam vrcholů (1,2,3) a seznam hran, jež jsou mezi těmito vrcholy. (1-2,1-3,2-3)

Výhody

přehledný, pokud máme hodně vrcholů, jež jsou spojeny malým počtem hran

Nevýhody

Při velkém počtu vrcholů se reprezentace stává nepřehlednou
lze použít pouze pro neorientovaný graf

Citace

Základní pojmy teorie grafů. [online] @2014 [cit. 9.12.2022] Mendelova univerzita.
Dostupné z: https://akela.mendelu.cz/~xjanca/II07-12.pdf
Úvod do teorie grafů. [online] @2014 [cit. 9.12.2022] Robert Mařík.
Dostupné z: https://user.mendelu.cz/marik/wiki-old/inzmat/slidy/grafy.pdf
Strom (graf) [online] @2022 [cit. 10.12.2022] Wikipedie.
Dostupné z: https://cs.wikipedia.org/wiki/Strom_(graf)¨
Graf [online] @2022 [cit. 10.12.2022] Algoritmy.net.
Dostupné z: https://www.algoritmy.net/article/1369/Graf
Matematická reprezentace grafu [online] @2022 [cit. 10.12.2022] Lukáš Jírovský.
Dostupné z: https://teorie-grafu.cz/zakladni-pojmy/reprezentace-grafu.php
Teorie grafů [online] @2013 [cit. 11.05.2023] RNDr. Martin Komenda, Ph.D. Masarykova univerzita.
Dostupné z: https://is.muni.cz/www/98951/41610771/43823411/43823458/Zaklady_informat/Teoreticke_zakla/TZI-teorie-grafu.pdf

Procházení grafů

procházení grafem do hloubky a do šířky, příklady - složitost

Grafové algoritmy – hledání minimální kostry

Primův algoritmus, Kruskalův algoritmus – principy algoritmů, složitost

Minimální kostra grafu je důležitým pojmem, využití má např. při řešení elektrických obvodů (při řešení pomocí Kirchhoffových zákonů potřebujeme sestavit dostatek lineárně nezávislých rovnic a získáme-li minimální kostru obvodu, je to poměrně jednoduché) nebo v Christofidově algoritmu pro heuristické řešení úlohy obchodního cestujícího.

Definice potřebných pojmů:

kostra souvislého grafu - takový faktor grafu, který je zároveň stromem
- faktor - je takový podgraf, který obsahuje všechny vrcholy grafu
- strom - je minimální souvislý graf s daným počtem vrcholů (neobsahuje cykly)
minimální kostra souvislého grafu - je kostra souvislého grafu (s ohodnocenými hranami), která má nejnižší váhu
- váha kostry - součet vah všech hran kostry

Algoritmy pro hledání minimální kostry se nazývají hladové (greedy). To je dáno tím, že se v každém kroku snaží získat co nejvýhodnější kus (zde hranu s nejmenším ohodnocením). U spousty problémů je tento přístup horší než porovnávání mezi různými variantami (spokojit se někdy s méně výhodným kusem), avšak u hledání minimální kostry vede vždy k optimálnímu výsledku.

Primův algoritmus

V roce 1929 vylepšil Vojtěch Jarník tzv. Borůvkův algoritmus. V roce 1957 ten samý algoritmus vymyslel i Robert Prim, podle kterého je ve světě znám.

Princip

Máme souvislý graf $ G $ s $ n $ vrcholy a s nezápornými vahami hran $ w $.

začneme z jednoho libovolného vrcholu.
přidáme takovou hranu, která má nejmenší váhu mezi hranami, které vedou z již vytvořeného podstromu do některého z dosud nepřipojených vrcholů grafu
opakujeme krok 3, dokud neprovedeme $ n - 1 $ kroků, poté algoritmus končí

Výhodné je, že nemusíme před začátkem hrany řadit a rovněž že nemusíme kontrolovat, zdali nevznikají cykly (vždy přidáváme nepřipojený vrchol), což je výpočetně náročné.

Složitost

Časová složitost algoritmu závisí na datové struktuře, která uchovává ohodnocení hran:

matice sousednosti - $ O(|U|^2) $
binární halda a seznam sousedů - $ O(|H| \cdot \log{|U|}) $
fibonacciho halda a seznam sousedů - $ O(|H| + |U| \cdot \log{|U|}) $

$ |H| $ je počet hran a $ |U| $ počet vrcholů.

Kruskalův algoritmus

Dalším algoritmem je ten popsaný Josephem B. Kruskalem v roce 1956. Kruskal, podovně jako Jarník, vycházel z práce Otakara Borůvky.

Princip

Máme les $ F $ (množinu stromů), ve kterém je každý vrchol grafu $ G $ samostatným podstromem a množinu $ S $ obsahující všechny hrany grafu $ G $.

z množiny $ S $ odebereme hranu s minimální váhou
- pokud tato hrana spojuje dva různé podstromy (dosud nespojené), přidáme ji do lesa $ F $ = tyto podstromy sloučíme do jednoho
- pokud ne, hranu zahodíme
krok jedna opakujeme do té doby, dokud je množina $ S $ neprázdná

Po skončení obsahuje les $ F $ jediný strom - minimální kostru grafu.

Složitost

je $ O(|H| \cdot \log{|U|}) $, kde $ |H| $ je počet hran a $ |U| $ počet vrcholů, pokud:
- seřadíme hrany podle vah v čase $ O(|H| \cdot \log{|H|}) $
- použijeme primitivnější datové struktury pro zaznamenávání příslušnosti hran k vrcholům (nevím které, ale pravděpodobně by to mohl být disjoint-set)
je $ O(|H| \cdot \alpha(|U|)) $, kde $ |H| $ je počet hran, $ |U| $ počet vrcholů a $ \alpha $ inverzní Ackermannova funkce, pokud:
- máme hrany již seřazené nebo jsme schopni je seřadit v lineárním čase
- použijeme sofistikovanější datové struktury pro zaznamenávání příslušnosti hran k vrcholům

Zdroje

KOVÁŘ, Petr. Úvod do Teorie grafů. 2016.
Přispěvatelé Wikipedie, Jarníkův algoritmus [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 19. 01. 2022, 23:35 UTC, [citováno 10. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Jarn%C3%ADk%C5%AFv_algoritmus&oldid=20853232
Přispěvatelé Wikipedie, Kruskalův algoritmus [online], Wikipedie: Otevřená encyklopedie, c2021, Datum poslední revize 7. 11. 2021, 21:18 UTC, [citováno 10. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Kruskal%C5%AFv_algoritmus&oldid=20618286

Grafové algoritmy – hledání minimální cesty

Dijkstrův algoritmus, Floyd–Warshallův algoritmus – principy algoritmů, složitost

Algoritmy pro hledání minimální cesty, jak jejich název napovídá, spočívají v nalezení nejkratší cesty mezi dvěma vrcholy grafu, tedy nalezení posloupnosti hran s nejnižším součtem vah.

Definice potřebných pojmů:

cesta - tah, ve kterém se neopakuje žádný vrchol
- tah - sled, ve kterém se neopakuje žádná hrana
  - sled - posloupnost hran, které na sebe vzájemně navazují

Dijkstrův algoritmus

Algoritmus pro hledání nejkratší cesty v grafu, popsaný Edsgerem Dijkstrou je konečný algoritmus (pro konečný vstup se vždy dostane do konce), který funguje v grafech s kladně ohodnocenými hranami. V každém průchodu cyklem grafu se přidává k výsledku právě jeden vrchol, maximální počet průchodů je tedy roven počtu vrcholů. Jedná se o variaci na prohledávání do šířky.

Dijkstrův algoritmus umí jedním průchodem nalézt nejkratší cestu do všech vrcholů grafu, nikoliv pouze do jednoho.

Princip

Máme:

graf $ G $
množinu vrcholů $ U $ grafu $ G $
- pro každý vrchol $ v $ z množiny $ V $ hodnotu $ d[v] $, která znamená nejkratší cestu k němu (známou v aktuálním cyklu)
  - počáteční vrchol $ s $ má $ d[s] = 0 $
  - všechny ostatní vrcholy mají na začátku $ d[v] = \infty $
- množinu nenavštívených vrcholů $ N $
- množinu navštívených vrcholů $ Z $
množinu hran $ H $ grafu $ G $

Postup:

vezmeme vrchol $ v $ z $ N $, který má nejnižší hodnotu $ d[v] $
pro každý vrchol $ u $, který je sousedem $ v $ a nepatří zatím do $ Z $ spočítáme jeho vzdálenost přes $ u $, a to takto: $ l = d[v] + m $, kde $ m $ je vzdálenost mezi $ v $ a $ u $ (váha hrany mezi nimi) a $ l $ výsledná vzdálenost vrcholu $ u $ od počátku
porovnáme $ l $ s $ d[u] $ (tedy s aktuální vzdáleností $ u $ od počátku)
- pokud je $ l $ nižší, nastavíme hodnotu $ d[u] $ na $ l $
- pokud je vyšší, neděláme nic
předešlé kroky opakujeme, dokud není množina $ N $ prázdná

Výsledkem je, že ke každému vrcholu $ v $ máme vzdálenost od $ s $, tedy $ d[v] $ a rovněž odkaz na předešlý vrchol v cestě, tudíž jsme schopni ji zpětně zrekonstruovat.

Složitost

pří použití obyčejného pole k uložení vzdáleností (nejnižší hodnota se hledá klasickým procházením tohoto pole) je $ O(|U|^2 + |H|) $
máme-li řídký graf (počet hran je mnohem menší než $ |U|^2 $), můžeme pomocí ukládání do seznamu sousedů a hledání nejnižší vzdálenosti binární nebo Fibonacciho haldou dosáhnout složitosti $ O(|H| + |U| \cdot \log{|U|}) $
$ |U| $ značí počet vrcholů a $ |H| $ počet hran grafu

Floyd–Warshallův algoritmus

Algoritmus poprvé popsaný Robertem Floydem a Stephenem Warshallem je schopný nalézt jedním průchodem nejkratší cestu mezi všemi dvojicemi vrcholů v grafu. Na rozdíl od Dijkstrova algoritmu podporuje i přítomnost hran s negativními vahami. Jeho výhodou je snadná implementace.

Princip

Máme:

graf $ G $
matici délek $ D $
- její hodnota na pozici $ i $ a $ j $ odpovídá váze hrany mezi vrcholy $ i $ a $ j $
  - z toho plyne, že na diagonále má samé nuly
  - není-li mezi vrcholy hrana, je na příslušné pozici $ \infty $
- lze říci, že obsahuje vzdálenosti uzlů, které jsou propojeny bez prostředníka

Postup:

Vytvoříme tři vnořené cykly s řídicími proměnnými $ i $, $ j $ a $ k $. Význam proměnných $ i $ a $ j $ odpovídá popisu výše (jedná se o indexy matice), $ k $ značí počet mezivrcholů, skrze které může propojovací cesta vést (vysvětleno dále). Všechny tři řídicí proměnné mají maximální hodnotu odpovídající řádu matice (počtu řádků či sloupců matice (vždy je čtvercová)).

V každé iteraci aplikujeme na aktuální hodnotu (na pozici $ i $, $ j $) funkci $ f(i, j, k) $, která zjišťuje, zdali mezi vrcholy $ i $ a $ j $ neexistuje kratší cesta přes $ k $ mezivrcholů. Pokud ano, upraví danou hodnotu.

Jak se hodnota $ k $ (a samozřejmě i $ i $ a $ j $) zvyšuje (iteracemi jejího cyklu), tak postupně dochází ke kontrole a případné úpravě všech hodnot v matici pro $ 0 $ mezivrcholů - počáteční stav, pro $ 1, 2, ..., d $, kde $ d $ je řád matice.

Složitost

Vzhledem k tomu, že se jedná o tři vnořené cykly, časová složitost algoritmu je $ O(|U|^3) $.

Zdroje

KOVÁŘ, Petr. Úvod do Teorie grafů. 2016.
Přispěvatelé Wikipedie, Dijkstrův algoritmus [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 13. 06. 2022, 04:08 UTC, [citováno 10. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Dijkstr%C5%AFv_algoritmus&oldid=21380350
Přispěvatelé Wikipedie, Floydův–Warshallův algoritmus [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 28. 03. 2023, 06:28 UTC, [citováno 10. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Floyd%C5%AFv%E2%80%93Warshall%C5%AFv_algoritmus&oldid=22581887
https://www.algoritmy.net/article/5207/Floyd-Warshalluv-algoritmus

Vyhledávání v textu

Princip vyhledávání hrubou silou, metody Rabin–Karp, Knuth–Morris–Pratt, Boyer–Moore, principy algoritmů - složitosti.

Problém vyhledávání v textu se dá vyjádřit jako problém nalezení určitého řetězce v jiném řetězci. Často tedy hledáme "jehlu v kupce sena". Často přidáváme k hledanému řetězci další podmínky, jako je například začínající písmeno nesmí být velké, řetězec musí začínat mezerou, před řetězcem se mohou nacházet další dva libovolné znaky apod. Nebo nás může zajímat kolikrát se daný řetězec v textu vyskytuje, či naopak, jaká je pozice prvního výskytu námi hledaného řetězce.

Úvodní pojmy

Haystack: Řetězec, ve kterém se snažíme nalézt jiný řetězec. Lze reprezentovat jako pole znaků (array).
Needle: Hledaný řetězec, také můžeme reprezentovat jako pole znaků.
Abeceda: Množina obsahující všechny znaky, jež se v tetu vyskytují.

Nyní budou následovat algoritmy pro vyhledávání v textu.

Jedná se o:

Naivní přístup
Rabin–Karp
Knuth–Morris–Pratt
Boyer–Moore

Naivní přístup (hrubá síla)

Náš haystack tvoří řetězec M: aaaaaaaaab a hledáme needle N ve tvaru aaab.

Naivní přístup spočívá v tom, že půjdeme index po indexu haystack řetězce a budeme ho porovnávat s needle řetězcem. Pokud bude znak v řetězci M souhlasit s prvním znakem v řetězci N, tak porovnáme druhý znak obou řetězců. Takto porovnáváme znaky dokud nedojdeme nakonec řetězce N, nebo dokud nenarazíme na znaky, jež se neshodují. V prvním případě jsme úspěšně nalezli hledaný řetězec. V tom druhém případě přejdeme na další znak v našem hlavním M řetězci a celý postup opakujeme, dokud neprojdeme celý řetězec M.

Průměrná složitost algoritmu: O(n+m); Pro více řetězců k: O(n+m)k
Nejhorší případ: O(n*m) - musíme projít celý hlavní řetězec a pro každý prvek hledaného řetězce projít celý hledaný řetězec až do konce a porovnat ho s hlavním řetězcem.

Rabin–Karp

Jedná se o vyhledávací algoritmus založený na principu hashovací funkce a pohyblivého okénka o velikosti vyhledávaného řetězce.

Nejprve algoritmus ohodnotí jednotlivé znaky abecedy.
Z těchto ohodnocení algoritmus vytvoří hash hodnotu pro vyhledávaný řetězec.
Algoritmus prochází vyhledávacím okénkem prvek po prvku hlavní řetězec, přičemž spočte hash hodnotu okénka v závislosti na tom, jaké znaky se v něm nacházejí.
Pokud hodnota hash okénka souhlasí s hash hodnotou vyhledávaného řetězce, tak algoritmus projde prvek po prvku tento subset znaků ve vyhledávacím okénku a porovná ho s vyhledávaným řetězcem podobně jako v případě naivního přístupu (prochází pouze podřetězec o velikosti vyhledávacího okénka, nikoliv celý řetězec, v němž vyhledáváme)
Pokud došlo ke shodě hash hodnot, ale řetězec ve vyhledávacím okénku neodpovídá tomu, který hledáme nazýváme tuto situaci spurious hit. Algoritmus pokračuje. Pokud odpovídá, našli jsme shodný řetězec.
Algoritmus pokračuje, dokud tímto způsobem neporovná celý hlavní řetězec s vyhledávaným řetězcem.

Výhodou tohoto algoritmu je možnost přeskakovat ty části hlavního řetězce, které mají jinou hash hodnotu nežli vyhledávaný řetězec.

Využití je hlavně v případech, kdy potřebujeme nalézt více řetězců k v hlavním řetězci. Jedno z hlavním využití tohoto algoritmu je například při kontrolách plagiátorství diplomových prací.

Průměrná složitost algoritmu: O(n+m) | Pro více řetězců k: O(n+km)
Nejhorší případ: O(n*m) - všechny nálezy budou spurious hit.

Knuth–Morris–Pratt

Algoritmus pracuje se dvěma řetězci, hlavní řetězec S a vyhledávaný řetězec W. Jeho hlavním cílem je redukce "backtrackingu", tedy nutnosti procházet znaky v řetězci S, které nepovedou ke shodě s řetězcem W.

Zavádí tedy prefix W. Jedná se o jeden či více znaků, kterými tento řetězec začíná. Pokud algoritmus nalezne shodu s S v prefixu, ale na nějakém dalším znaku se již S a W neshoduje, můžeme tyto znaky přeskočit. Pakliže algoritmus nalezne shodu s prefixem, bude v dalším kroku pokračovat od tohoto prefixu.

Průběh algoritmu:

Ulož si prefix W (jeden či více znaků).
Začni prvním prvkem v S a porovnej s prvním prvkem W. Pokud se neshoduje, opakuj tento krok s dalším prvkem W, dokud nenarazíš na shodu.
Pokud jsme našli shodu, porovnáváme následující prvek W s následujícím prvkem S. Pokud máme shodu, přecházíme na další prvek W a S. Pokud v průběhu nacházíme v S prvky, které odpovídají prefixu, ukládáme je do samostatného pole a číslujeme je.
Při neshodě algoritmus začíná tam, kde nalezl prefix. Pokud žádný prefix nenalez, začíná na dalším prvku v S, jež se nachází hned za tím, u kterého došlo k neshodě.
Postup se opakuje dokud algoritmus neprojde celý řetězec S.

Průměrná složitost algoritmu: O(n+k) kde n je velikost S a k je velikost W. Tato složitost je také jediná možná, díky tomu, že algoritmus si udržuje pozici nalezeného prefixu v S při porovnávání s W a na tuto pozici je schopen se vrátit, čímž přeskakuje hodnoty v S kterými W nezačíná. Není zde nejhorší případ.

Boyer–Moore

Tento algoritmus si zakládá na obráceném porovnávání. Namísto toho, aby porovnával prefix, tedy začátek hledaného řetězce W s hlavním řetězcem S, porovnává suffix, tedy koncové znaky řetězce W s řetězcem S.

V první fázi jsou řetězce S a W srovnány "pod sebe" a algoritmus porovnává znaky zprava doleva. Pokud je nalezen charakter v S, který není v řetězci W, tak zde nemůže být žádná shoda a celý řetězec W může být přesunut tak, aby začínal za pozicí, na které se nachází neshodný charakter v S.

To zda je tento posun ideální či nikoliv je třeba nejdříve ověřit. Algoritmus to dělá pomocí dvou heuristik:

Bad Character Heuristics
Good Suffix Heuristics

Bad Character Heuristics

Jedná se o případ, kdy nalezneme charakter v S, který nesedí s W.

Pokud charakter není obsažen ve vyhledávaném řetězci W, posuneme celý řetězec W za tento charakter v S.
Pokud je charakter obsažený ve vyhledávaném řetězci, posuňme vyhledávaný řetězec W tak, aby se charakter ve W shodoval s tím v S.


obr. 1: Hledaný řetězec W obsahuje Bad Character Převzato z: https://www.javatpoint.com/daa-boyer-moore-algorithm


obr. 2: Hledaný řetězec W neobsahuje Bad Character Převzato z: https://www.javatpoint.com/daa-boyer-moore-algorithm

V některých případech se může tímto způsobem řetězec W začít vůči S posouvat zpět, klidně do negativních hodnot. Abychom tomuto zabránily, ukládáme si poslední nalezenou pozici každého charakteru, jež tvoří set W (Někdy také nazývaný abeceda řetězce W)

Good Suffix Heuristics

Good suffix je takový suffix, který se úspěšně shoduje s charaktery, nalezenými v S. Pokud nalezneme pomocí Bad Character Heuristics špatný charakter, který by znamenal negativní posun, zkontrolujeme, zdali souhlasí suffix W s charaktery v S. Pokud ano, posuneme řetězec W o délku, na které se suffix nachází. (Před suffixem se nachází bad character, není tedy možné aby jsme nalezli shodu při posunu zpět)


obr. 3: Posun po aplikování Good Suffix Převzato z: https://www.javatpoint.com/daa-boyer-moore-algorithm

Průběh algoritmu:

Řetězce S a W jsou zarovnány tak, že začínají pod sebou.
Kontrolují se shodné znaky zprava doleva.
V případě neshody aplikuj Bad Character Heuristics, v případě že toto vyvolá negativní posun, tak aplikuj Good Suffix Heuristics
Pokračuj znovu v kontrole zprava doleva.
Opakuj postup, dokud nenajdeš shodný řetězec

Nejhorší možná složitost algoritmu: O(m+n) pokud S neobsahuje W nebo O(m*n) pokud S obsahuje W.

Zdroje

Wikipedia: Open encyclopedia: String-searching algorithm [online]. c2023 [citováno 23. 04. 2023].
Dostupný z: https://en.wikipedia.org/wiki/String-searching_algorithm
Parewa Labs Pvt. Ltd.: Rabin-Karp Algorithm [online]. c2023 [citováno 23. 04. 2023].
Dostupný z: https://www.programiz.com/dsa/rabin-karp-algorithm
Javapoint: The Rabin-Karp-Algorithm [online]. c2023 [citováno 23. 04. 2023].
Dostupný z: https://www.javatpoint.com/daa-rabin-karp-algorithm
GeeksForGeeks: Rabin-Karp Algorithm for Pattern Searching [online]. c2023 [citováno 23. 04. 2023].
Dostupný z: https://www.geeksforgeeks.org/rabin-karp-algorithm-for-pattern-searching/
Educative, Inc.: What is the Knuth-Morris-Pratt algorithm? [online]. c2023 [citováno 23. 04. 2023].
Dostupný z: https://www.educative.io/answers/what-is-the-knuth-morris-pratt-algorithm
Wikipedia: Open encyclopedia: Knuth–Morris–Pratt algorithm [online]. c2023 [citováno 23. 04. 2023].
Dostupný z: https://en.wikipedia.org/wiki/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm
Javapoint: The Boyer-Moore Algorithm [online]. c2023 [citováno 23. 04. 2023].
Dostupný z: https://www.javatpoint.com/daa-boyer-moore-algorithm

Neuronové sítě, základní pojmy

neuron, synapse, axon, dendrit, váha, práh, aktivační funkce

Úvod

Koncept neuronový sítí byl v počátcích inspirován a vytvářen na základě biologické analogie s nervovým systémem. Vezeme si příklad hodu míčem. Co se stane, pokud cíl při hodu mineme? Pomocí receptorů (například vizuálních) máme možnost výsledek vyhodnotit a v případě toho, že cíl například přehodíme, upravit sílu hodu.

Zjistili jsme tedy odchylku od požadovaného ideálního stavu na výstupu a na základě zpětné vazby trénujeme náš nervový systém tak, aby byl schopen danou úlohu plnit co nejlépe. Člověk tedy získává prostřednictvím svého nervového systému i schopnost učit se a zapamatovat si získané informace.

Celý nervový systém člověka je představován obrovským počtem navzájem provázaných biologických funkčních jednotek, neuronů. Například mozek obsahuje až 10¹¹ neuronů, kde každý neuron může mít až 5000 spojů s ostatními neurony. Tyto spoje se nazývají synapse, mohou mít jak excitační, tak inhibiční charakter, mohou tedy vést k posílení, či potlačení odezvy neuronu na přicházející podněty, vzruchy.

Pokud se budeme držet popisu biologického neuronu, který nás má dovést k matematickému modelu, můžeme konstatovat, že každý neuron se skládá z z těla a dvou typů výběžků: dendritů a axonu.

Dendrit: Z pohledu šíření vzruchu do těla se jedná o vstupy neuronu.
Axon: Axon představuje výstup neuronu, kterým se siří vzruch z těla neuronu a který je pomocí synapsí napojen na dendrity neuronů dalších


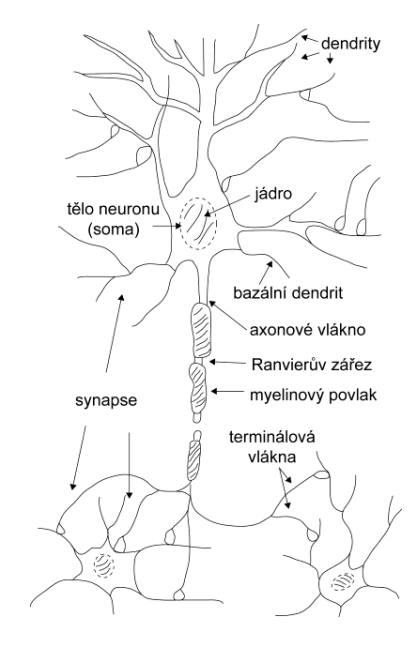obr. 1: Biologický neuron Převzato z: https://portal.matematickabiologie.cz/res/f/neuronove-site-jednotlivy-neuron.pdf

Matematický model a aktivní dynamika neuronu

Neuronová síť je tvořena matematickými neurony, primitivními jednotkami kde každá zpracovává vstupní signály a generuje výstup.


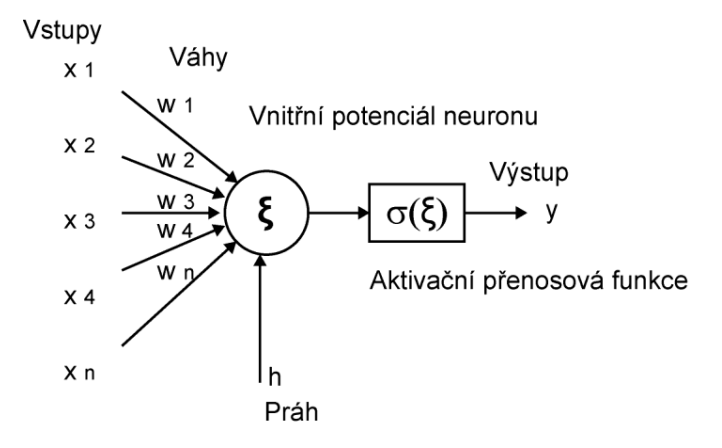obr. 2: Matematický neuron - model Převzato z: https://portal.matematickabiologie.cz/res/f/neuronove-site-jednotlivy-neuron.pdf

Neuron lze rozdělit na několik částí:

Synapse: Přivádějí vstupy X do těla neuronu. Každá synapse je ohodnocena vahou, tedy důležitostí této synapse. Můžeme říct, že každá synapse, každý vstup, je pro neuron jinak důležitý. Vstupy mohou být buď inicializační (jedná se o vstupní vrstvu) nebo se může jednat o výstupy jiných neuronů.
Váha: Číselná hodnota, jež udává, jaký vliv má hodnota na vstupu.
Tělo neuronu: Do těla neuronu jsou svedeny všechny vstupy skrze synapse + práh, který je často vedený také jako vstup a na základě těchto hodnot se zde získává vnitřní potenciál neuronu
Práh: Z praktických důvodů se práh zpravidla modeluje jako jedna z vah tak, že vstupní vektor i vektor vah je rozšířen o nultou pozici. Vstup na nulté pozici je vždy uvažován za rovný 1 a nultá váha je nastavena na hodnotu rovnu –h. V takovém případě se práh stává jednou z vah a v průběhu trénování podléhá adaptaci.
Vnitřní potenciál neuronu: Značí se $\xi$ (Ksí). Jedná se o hodnotu, kterou dostaneme tak, že každý vstup X vynásobíme vahou synapse. Vstupy v těle neuronu sečteme a odečteme práh. Tato hodnota je poté vstupem do Aktivační přenosové funkce.
Aktivační funkce: Značí se $\delta$ (Delta). Je obecně nelineární funkcí transformující hodnotu vnitřního potenciálu neuronu.


obr. 3: Výstup neuronu, kde $\delta$ je aktivační funkcí a $\xi$ vnitřním potenciálem neuronu. (Práh je vedený jako vstup na 0-t= pozici) Převzato z: https://portal.matematickabiologie.cz/res/f/neuronove-site-jednotlivy-neuron.pdf

Fungováním neuronových sítí jako celku se dále zaobírá okruh Základní modely neuronových sítí.

Zdroje

HOLČÍK, Jiří, KOMENDA, Martin (eds.) a kol. Neuronové sítě - jednotlivý neuron. [online]. Brno: Masarykova univerzita, @2015 [cit. 2023-01-24]. Dostupné z: https://portal.matematickabiologie.cz/res/f/neuronove-site-jednotlivy-neuron.pdf

Základní modely neuronových sítí

perceptron a RBF, typické aktivační funkce neuronů a topologie neuronových sítí

Tento okruh vychází ze znalostí toho, co je to neuron a známe základní pojmy, jež se k neuronu vztahují. Tyto základní pojmy, společně s popisem neuronu lze najít v okruhu Neuronové sítě, základní pojmy.

Základní topologie neuronové sítě

Neuronová síť je tvořena z neuronů a vazeb mezi těmito neurony. Klasická neuronová síť se skládá ze tří typů vrstev:

vstupní vrstva:
- tato vrstva zpracovává zadané vstupy
N skrytých vrstev:
- každá z těchto vrstev přijímá jako vstupy výstupní hodnoty aktivačních funkcí předchozí vrstvy
- ne vždy jsou potřeba skryté vrstvy, záleží na konkrétním typu neuronové sítě a toho, čeho chceme její aplikací dosáhnout
- obecně platí, že pokud nemůžeme výstupy klasifikovat na základě lineární regrese, je potřeba použít skryté vrstvy
- příklad rozhodnutí, zdali skrytou vrstvu použít, či nikoliv, je uveden zde
výstupní vrstva:
- vstupy jsou výstupní hodnoty aktivačních funkcí předchozí vrstvy a výstupem je/jsou výsledky (počet výsledků odpovídá počtu neuronů ve výstupní vrstvě)


obr. 1: Příklad podoby neuronové sítě, kde se počet skrytých vrstev = 2
dostupné z: https://www.baeldung.com/cs/hidden-layers-neural-network

Druhy topologií neuronových sítí

Topologii můžeme dělit na dva druhy:

dopředná neuronová síť
- signál proudí jedním směrem (dopředu)
- perceptron i RBF jsou dopředné neuronové sítě
- jednovrstvá dopředná síť:
  - neobsahuje skrytou vrstvu, vstup je přímo napojený na výstup
- vícevrstvá dopředná síť:
  - obsahuje jednu či více skrytých vrstev
síť se zpětnou vazbou/rekurentní neuronová síť
- signál může proudi nejen dopředu, ale i do předchozích vrstev (tento okruh se zaobírá dopřednými neuronovými sítěmi, více o rekurentních sítích lze nalézt v okruhu Rekurentní neuronové sítě)
- plně rekurentní síť:
  - každý neuron je propojený s každým a propojení fungují obousměrně jako vstup i výstup
  - Jordan síť:
    - výstupní vrstva je napojena na vstupní vrstvu sloužící jako zpětná vazba


obr. 2: Plně rekurentní topologie, kde se počet skrytých vrstev = 2
dostupné z: https://www.tutorialspoint.com/artificial_neural_network/artificial_neural_network_building_blocks.htm


obr. 3: Plně rekurentní topologie, kde se počet skrytých vrstev = 1
dostupné z: https://www.tutorialspoint.com/artificial_neural_network/artificial_neural_network_building_blocks.htm

Základní aktivační funkce

Účelem aktivační funkce je rozhodnout, jaká bude výstupní hodnota neuronu na základě hodnoty jeho vnitřního stavu. Každá aktivační funkce má své využití, některé aktivační funkce se hodí používat pouze v určitých vrstvách.

Rozebereme si následující druhy používaných aktivačních funkcí:

Lineární
Sigmoid
Tangens hyperbolická funkce (Tanh funkce)
RELU funkce
Softmax funkce

Lineární aktivační funkce

rovnice: $ y = x $
pokud máme na všech vrstvách lineární aktivační funkci, tak platí, že nezávisle na počtu vrstev je aktivační funkce výstupní vrstvy pouze lineární funkce vstupní vrstvy
použití:
- pouze na jednom místě, například ve výstupní vrstvě
- hodí se na řešení lineárně regresních problémů (dělení do kategorií)

Sigmoid aktivační funkce

rovnice: $ y = \frac{1}{1 + e^{-x}} $
nelineární funkce, na základě tvaru křivky a toho, že v intervalu $<-2, 2>$ hodnoty $y$ rostou velmi rychle lze vidět, že i malá změna $x$ má velký vliv na výstupní hodnotu $y$
rozsah výstupních hodnot $je <0, 1>$
použití:
- klasicky ve výstupní vrstvě binárních klasifikátorů, kde výsledek může být buď 0, nebo 1
- výstupní hodnota této funkce se pohybuje mezi 0 a 1, funkce tedy může říct, že výstup je 1, pokud je spočtená hodnota větší než například 0,5.


obr. 4: Sigmoida
dostupné z: https://www.geeksforgeeks.org/activation-functions-neural-networks/

Tanh aktivační funkce

rovnice:


obr. 5: Tanh rovnice
dostupné z: https://www.geeksforgeeks.org/activation-functions-neural-networks/

jedná se o posunutou sigmoid funkci (často se využívá namísto této funkce)
rozsah výstupních hodnot je $<-1, 1>$
použití:
- obvykle se využívá ve skrytých vrstvách
- protože rozsah výstupu funkce je mezi -1 a 1, používá se ke stáhnutí středních hodnot k 0 a vycentrování dat, umožňuje tedy jednotlivým vrstvám jednodušší proces učení.


obr. 6: Tanh funkce
dostupné z: https://www.geeksforgeeks.org/activation-functions-neural-networks/

RELU aktivační funkce

rovnice: $A(x) = max(0,x)$
- vrací $x$ pokud je $x$ pozitivní, jinak vrací 0
jedná se o nejvíce používanou funkci, hlavně ve skrytých vrstvách
rozsah výstupních hodnot je $<0, \infty>$
použití:
- RELU je méně výpočetně náročná nežli Sigmoid nebo Tanh funkce
- povětšinou svým výstupem aktivuje jen pár dalších neuronů, je tedy více vhodná i k následnému učení


obr. 7: RELU funkce
dostupné z: https://www.geeksforgeeks.org/activation-functions-neural-networks/

Softmax aktivační funkce

jedná se o typ sigmoid funkce
rozsah výstupních hodnot je $<0, 1>$
použití:
- pokud se snažíme zařadit data do více tříd, tak se funkce používala ve výstupní vrstvě při klasifikaci obrazu
- funkce umožňuje namapovat velké hodnoty $x$ do intervalu $<0, 1>$
- funkce se nyní často používá ve výstupní vrstvě klasifikátorů, kdy je třeba určit pravděpodobnost, s jakou data spadají do určité třídy


obr. 8: Softmax funkce
dostupné z: https://www.geeksforgeeks.org/activation-functions-neural-networks/

Jak se rozhodnout, kterou funkci použít?

pokud je náš výstup v podobě binárního klasifikátoru, použijeme Sigmoid aktivační funkci pro výstupní vrstvu
pokud potřebujeme určit s jakou pravděpodobností data spadají do určité třídy a je techto tříd více (multi-class classification), použijeme Softmax aktivační funkci
pokud nevím, jakou funkci použít pro skrytou vrstvu, použiji RELU aktivační funkci, protože se momentálně jedná o nejvíce používanou aktivační funkci ve skrytých vrstvách

Modely neuronových sítí

Modely neuronových sítí se mohou lišit buď topologií nebo postupem výpočtu vnitřního potenciálu neuronu. V tomto okruhu budou probírány dva z těchto modelů:

Perceptron
RBF (Radial Basic Network)

Perceptron

Jedná se o nejjednodušší model dopředné neuronové sítě. Zároveň se jedná i o matematický model biologického neuronu. Můžeme říct, že libovolný model je složený z perceptronů, ale pokud se koukáme na perceptron jako na samostatný model, jedná se o binární klasifikátor, který na základě vstupů spočte svůj vnitřní stav a svůj vnitřní stav předává jako argument aktivační funkci. Perceptron řeší lineárně separovatelné problémy. Pokud je třeba dělit do více tříd než dvou, používá se tzv. Multi-layer Perceptron, který mezi vstupní a výstupní vrstvou obsahuje další, skryté vrstvy.

Aktivační funkce vypadá následovně:


obr. 9: Aktivační funkce perceptronu
dostupné z: https://www.geeksforgeeks.org/activation-functions-neural-networks/

w je vector vah vstupů a x je vektor hodnot na vstupech
b je bias, nebolí práh
- tento práh si perceptron upravuje sám na základě toho, jak moc se lišila výsledná hodnota od hodnoty očekávané
- více o tomto tématu v okruhu Učení bez učitele
všimněme si, že model perceptronu je stejný, jako obecný model neuronu z okruhu Neuronové sítě, základní pojmy
abychom dosáhli požadovaného výsledku aktivační funkce, tak se nejčastěji používá sigmoid aktivační funkce


obr. 10: Model Perceptronu
dostupné z: https://www.geeksforgeeks.org/activation-functions-neural-networks/


obr. 11: Perceptron - neuronová síť (žlutá je vstupní vrstva a oranžová je vrstva výstupní)
dostupné z: https://towardsdatascience.com/the-mostly-complete-chart-of-neural-networks-explained-3fb6f2367464

RBF (Radial Basis Function network)

Na rozdíl od neuronových sítích založených čistě na Perceptronech využívají RBF sítě RBF neurony.

RBF nepočítá svůj vnitřní stav jako součin vektorů vstupů a vah (w a x), ale má v sobě uložený jeden vektor z trénovací množiny, označený jako střed. Tyto středy se dají ideálně získat pomocí K-means algoritmu. Tento vektor (střed) se používá k měření Euklidovské vzdálenosti od vstupních vektorů. Výsledek poté pošle do aktivační funkce, která spočte, jak moc je aktuální vektor vstupů podobný středu.
aktivační funkce RBF neuronu je Gaussova funkce


obr. 12: Aktivační funkce RBF neuronu, kde x je jeho vnitřní stav
dostupné z: https://en.wikipedia.org/wiki/Radial_basis_function_network

výstupem RBF aktivační funkce je hodnota, která určuje, jak moc je vstupní set podobny středu
tyto hodnoty se sečtou ve výstupní vrstvě
RBF neurony jsou náchylnější ke skončení v lokálním minimu, ale naopak umí dobře pracovat s odlehlými hodnotami - velké změny v parametrech neuronu způsobí malý posun u hodnot, jež jsou daleko od středu
RBF sítě mají obvykle jednu skrytou vrstvu, která obsahuje RBF neurony a lineární výstupní vrstvu
výstupem z celé této sítě je tedy skalární součin vektoru výstupu z RBF vrstvy a vah synapsí vedoucí ze skryté vrstvy do výstupní vrstvy
RBF se tedy liší od Multi-layer Perceptron sítě jinou aktivační funkcí a způsobem použití


obr. 13: RBF síť s jednou skrytou vrstvou (zelená), ve které se nacházejí RBF aktivační funkce (výstup těchto funkcí vede do výstupní vrstvy, která již nemusí být RBF)
dostupné z: https://towardsdatascience.com/the-mostly-complete-chart-of-neural-networks-explained-3fb6f2367464

Zdroje

Baeldung. Hidden Layers in a Neural Network. [online]. @2023 [cit. 2023-04-24].
Dostupné z: https://www.baeldung.com/cs/hidden-layers-neural-network
Great Lakes E-Learning Services Pvt. Ltd. Types of Neural Networks and Definition of Neural Network. [online]. @2023 [cit. 2023-04-24].
Dostupné z: https://www.mygreatlearning.com/blog/types-of-neural-networks/
Towards Data Science. Types of Neural Networks and Definition of Neural Network. [online]. @2023 [cit. 2023-04-24].
Dostupné z: https://towardsdatascience.com/the-mostly-complete-chart-of-neural-networks-explained-3fb6f2367464
GeeksForGeeks. Activation functions in Neural Networks. [online]. @2023 [cit. 2023-04-24].
Dostupné z: https://www.geeksforgeeks.org/activation-functions-neural-networks/
Wikipedia - Open encyclopedia. Perceptron. [online]. @2023 [cit. 2023-04-24].
Dostupné z: https://en.wikipedia.org/wiki/Perceptron
TutorialsPoint. Artificial Neural Network - Building Blocks. [online]. @2023 [cit. 2023-04-24].
Dostupné z: https://www.tutorialspoint.com/artificial_neural_network/artificial_neural_network_building_blocks.htm
Luthfi Ramadhan. Radial Basis Function Neural Network Simplified. [online]. @2021 [cit. 2023-04-24].
Dostupné z: https://towardsdatascience.com/radial-basis-function-neural-network-simplified-6f26e3d5e04d
Wikipedia - Open encyclopedia. Radial basis function network. [online]. @2023 [cit. 2023-04-24].
Dostupné z: https://en.wikipedia.org/wiki/Radial_basis_function_network

Učení neuronové sítě

Cíl, pojmy: zevšeobecnění, přeučení, problém uváznutí v lokálním minimu, trénovací, testovací, validační množina

Činnost neuronových sítí lze rozdělit do dvou fází:

Učení (adaptace)
Života

Ve fázi učení se znalosti ukládají do synaptických vah neuronové sítě, lze to znázornit jako:

\[\frac{\delta W}{\delta t} \neq 0\]

kde $W$ je matice všech synaptických vah a $t$ je čas. Synaptické váhy se v průběhu učení mění.

Fáze života:

\[\frac{\delta W}{\delta t} = 0\]

v této fázi se získané znalosti využívají ve prospěch řešení nějakého problému. Synaptické váhy se v této fázi nemění.

Definice učení

Jde de facto o proces získávání / uchování znalostí, založený na změně synaptických vah měnících se dle pravidel determinovaných typem učení neuronové sítě.
Učením se rozumí adaptace neuronové sítě, které po této fázi bude nositelkou znalostí získaných v průběhu učení.
jedná se o optimalizační úlohu, která najde pro příslušnou trénovací množinu dat takovou konfiguraci vah, kdy je průměrná chyba sítě přes celou trénovací množinu menší, než požadované kritérium.

Učení lze realizovat deduktivní a induktivní metodou, přičemž u induktivní metody se vyvozují generalizovaně platné závěry na základě pozorování množiny jevů (syntetický přístup k učení). Deduktivní metoda využívá pouze jeden jev a jeho pozorování a analyzování (analytický přístup k učení).

Nejčastější metodou učení u neuronových sítí je metoda induktivní, a to buď s učitelem - poskytuje správnou informaci o požadovaném výstupu NS, nebo bez učitele - NS nedostává informaci o požadovaném výstupu, ale odvozuje si ji sám na základě zpětné vazby.

Učení NS se dále provádí prostřednictvím gradientních metod či přírodou inspirovaných algoritmů (genetický algoritmus).

Pojmy související s učením NS

Trénovací množina: množina vzorů určená k trénování neuronové sítě - nacházení vztahu mezi vstupy a výstupy (provádí regresní analýzu, čímž se učí)
Testovací množina: množina vzorů určená pro testování neuronové sítě - určení kvality naučeného systému
Vzor: element datového souboru určeného pro zpracování NS
- Vzor bývá v páru - vstupní vektor (na vstupech neuronové sítě), výstupní vektor (požadovaná hodnota výstupů)
- sítě SOM (Samoorganizující se mapy) výstupní vektor nepotřebují
Validační množina: množina vzorů použita k testování přímo v průběhu učení - zabraňuje se tak přeučení NS; používá se pro případnou změnu parametrů učení, aby se předešlo overfittingu-přeučení; vyhodnocuje-li systém se shodnou úspěšností trénovací i validační množinu, je pravděpodobně správně naučen; pokud systém vykazuje vyšší úspěšnost u vyhodnocení trénovací množiny, je nejspíše přeučený
Vybavení: předložení jednoho vzoru NS a výpočet výstupu NS
Iterace: předložení vzoru NS, provedení Vybavení a následně jednoho kroku učení
Epocha: provedení iterace pro všechny vzory z trénovací množiny
Učení: proces výpočtu váhových synaptických koeficientů/vah na základě trénovací množiny
- učení se skládá z epoch
Přeučení: nadměrná doba učení - je provedeno příliš mnoho epoch učení
- toto způsobuje nadměrnou chybu pro netrénovaná data (zhorší se zevšeobecnění)
Lokální minimum: parazitní minimum na chybové/energetické hyperploše, jehož chyba je větší než chyba globálního minima
Zevšeobecnění: schopnost NS správně reagovat na neučená data
Hebbovo pravidlo: pro úpravu vah, posiluje vztahy mezi neurony, jež vykazují podobné reakce na stejné podněty
Delta pravidlo: pro úpravu vah v učícím algoritmu Back Propagation

Hebbův zákon učení

Hebbův zákon je základním prvkem téměř všech algoritmů učení NS (vyjma Back Propagation). Hebbův zákon popisuje algoritmus modifikace hodnot synaptických vah v nervových systémech živých organismů. Je založen na předpokladu, že jsou-li dva navzájem propojené neurony ve stejném okamžiku aktivní, tak jejich vzájemná vazba je zesílena. V opačném případě (nejsou-li aktivní) se vazba mezi nimi oslabuje. Je-li aktivní pouze jeden neuron synapse nejsou modifikovány.

Neurony mají tedy dva stavy: aktivní a neaktivní.

Vzorec Hebbova zákona

\[\Delta W_{ij} = \eta \times x_i (t) \times x_j(t)\]

$\Delta W_{ij}$ - rozdíl vah
$x_j$ - presynaptický stav j-tého neuronu
$x_i$ - postsynaptický stav i-tého neuronu
$\eta$ - eta, zrychlení/zesílení procesu učení

Algoritmus učení NS (s učitelem)

Náhodně inicializujeme váhy v neuronové síti
Vezmeme pár vektorů I/O z trénovací množiny dat a vstupní vektor přiložíme na vstup sítě
Vypočteme výstupy sítě
Porovnáme výstup sítě z částí výstup z páru I/O a vypočteme odchylku
Na základě odchylky upravíme váhy sítě $w$
Dokud nevyčerpáme celou trénovací množinu, pokračujeme bodem 2
Pokud je průměrná chyba přes celou trénovací množinu vyšší, než požadované kritérium, pokračujeme opět bodem 2
Síť je naučena, KONEC

GRADIENT

Diferenciální operátor (řecky nabla, symbol $\nabla$). Je-li aplikován na funkci o vícero proměnných, je jejím výsledkem vektor parciálních derivací dle všech proměnných této funkce.

**GRADIENT** je směr největšího růstu funkce v daném bodě na ploše funkce f.


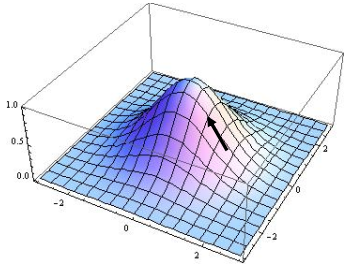obr. 1: Gradient
zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.

Uváznutí v lokálním minimu (Gradientní metoda učení)

Představme si kuličku reprezentující hodnoty všech vah a kutálející se dle gradientu E, tj. dle gradientu se přičte ke každé váze $\Delta w$ dle hodnoty gradientu násobeného parametrem $\eta$ - viz Delta pravidlo v otázce č. 1.15 (Učení neuronové sítě metodou s učitelem).

Dospěje-li kulička do lokálního minima, krok kterýmkoli směrem znamená navýšení chyby. Za "kopec" do globálního minima kulička nevidí (algoritmus nevidí) a tudíž končí s chybou lokálního minima.


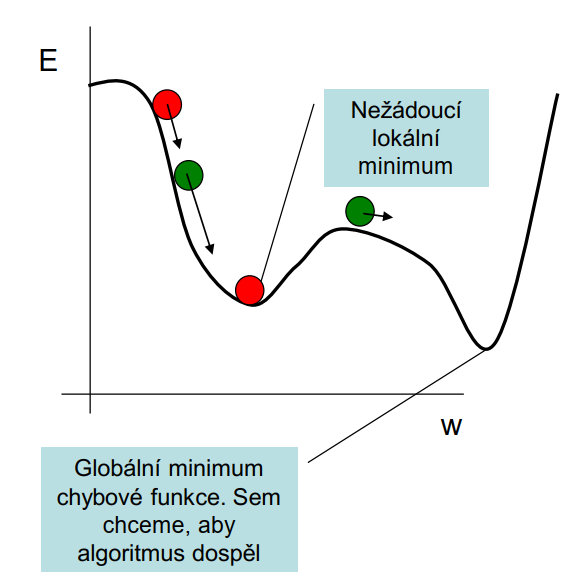obr. 2: Problém lokálního minima
zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.

Řešení uváznutí v lok. minimu

Častým řešením může být zavedení setrvačnosti (parametr $\alpha$). Kulička získá setrvačnost a nezávisle na gradientu se překulí přes svah do globálního minima. Setrvačnost musí být dostatečná, aby mohla kulička svah překonat, jinak bude oscilovat v lokálním minimu, dokud se nezastaví.

Správné nastavení parametrů $\eta$ a $\alpha$
Výběr vzorů s trénovací množiny v náhodném pořadí
- obvykle se používá sekvenční (postupný) výběr vzorů, kdy se pořadí vzorů nemění v průběhu epochy. Toto někdy vede „mylným závislostem“, které si neuronová sít během učení vyvodí a to může někdy vést do lokálního minima (odpovíte stejně rychle na otázku kolik je 6x9 nebo 9x6)
Strukturou trénovací množiny - stejné zastoupení vzorů ve všech třídách a zředění dat (vynechání obdobných vzorů v rámci kategorie)
Použití gradientní metody s proměnným krokem (mění se parametr $\eta$), je-li parametr stejný, považujeme krok algoritmu za konstantní

Trénovací množina

Příprava trénovací množiny

dostupná data rozdělíme na testovací a trénovací množinu
vzory ze všech tříd by měly mít stejné procentní zastoupení
normalizace vstupních dat
- změna měřítka
- transformace skrze nelineární funkci: potlačení velkých hodnot, zdůraznění malých hodnot

Popis a vzorec

Trénovací množina obsahuje prvky popisující řešený problém, přičemž každý vzor trénovací množiny popisuje jakým způsobem jsou excitovány neurony vstupní a výstupní vrstvy.

Formálně lze za trénovací množinu $T$ považovat množinu prvků (vzorů), které jsou definovány uspořádanými dvojicemi takto:

\[T = {(x_k t_k) | x_k \in {0, 1}_n, t_k \in {0, 1}_m, k = 1, ...q}\]

$q$: počet vzorů trénovací množiny
$x_k$: vektor excitací vstupní vrstvy tvořené n neurony
$t_k$: vektor excitací výstupní vrstvy tvořené m neurony

ZDROJE

SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.
OLEJ, Vladimír a Hájek PETR. Úvod do umělé inteligence: Moderní přístupy - Distanční opora. Univerzita Pardubice: Fakulta Ekonomicko-správní, 2010, 95s. ISBN 978-80-7395-307-2.
VOLNÁ, Eva. Neuronové sítě 1. 2 vyd. Ostrava: Ostravská univerzita v Ostravě, 2008, 87 s. Dostupné také z: https://web.osu.cz/~Volna/Neuronove_site_skripta.pdf

Učení neuronové sítě metodou s učitelem

Princip algoritmu zpětného šíření chyby - Backpropagation, parametry algoritmu, delta pravidlo

Učení s učitelem je primárně založeno na minimalizaci chyby mezi aktuální a požadovanou odezvou neuronové sítě. Právě ona odezva sítě zde hraje roli učitele.

Hledaná funkce je zde vždy zadána prostřednictvím dvojice hodnot, hodnot vstupů $x_k$ a hodnot požadovaných výstupů $t_k$. Během procesu učení nám síť vrací skutečné výstupní hodnoty $y_k$ coby výstupní odezvu NS na daný vstupní signál. Zároveň dochází k úpravě vah za účelem minimalizace chyby, respektive dosažení co největší shody mezi skutečným výstupem a tím požadovaným.

Cílem samotného učení je hledání minima chybové (energetické) funkce:

\[E(w) = \sum_{l = 1}^q E_l (w)\]

$q$: počet vzorů trénovací množiny
$l$: $l.$ tréninkový vzor
$w$: konfigurace vah v dané NS

Je to součet parciálních chyb sítě $E_l(w)$ vzhledem k jednotlivým tréninkovým vzorům.

Parciální chyba neuronové sítě $E_l(w)$ pro $l.$ tréninkový vzor ($l = 1, ...., q$) je úměrná součtu mocnin odchylek (rozdílů) skutečných hodnot výstupu sítě $y_k$ pro vstup $l$-tréninkového vzoru od požadovaných hodnot výstupů u tohoto vzoru $t_k$:

\[E_l(w) = \frac{1}{2}\sum_{k \in {Y}} (y_k - t_k)^2\]

ZÁPIS - PŘEDNÁŠKY SKRBEK: \[E_l(w) = \frac{1}{2}\sum_{j=1}^M \sum_{i=1}^N (y_i^{(j)} - d_i^{(j)})^2\]

N: počet výstupů neuronové sítě
M: počet vzorů v trénovací množině
$y_i^{(j)}$: i-tý výstup j-tého vzoru z trénovací množiny

Vícevrstvá neuronová síť a algoritmus BACKPROPAGATION

Vícevrstvá NS je nejrozšířenější variantou propojení neuronů se sigmoidní aktivační funkcí (způsob jakým se ze vstupu počítá výstup neuronu). Zatímco algoritmus Backpropagation (zpětné šíření chyby) je nejrozšířenějším adaptačním algoritmem v těchto vícevrstvých neuronových sítích.

Vícevrstvá síť má vstupní vrstvu $X$, skrytou vnitřní vrstvu $Z$ a výstupní vrstvu neuronů $Y$. Jednotlivé neurony jsou značeny:

$X_i, i = 1, ..., n$
$Z_j, j = 1, ..., p$
$Y_k, k = 1, ..., m$

Neurony ve výstupní a vnitřní vrstvě musí mít definovaný tzv. Bias, který odpovídá váhové hodnotě přiřazené spojení mezi příslušným neuronem a fiktivním neuronem, jehož aktivace je vždy 1.

Označení Bias pro j-tý neuron ve vnitřní vrstvě je $v_{0}{j}$ a ve výstupní vrstvě k-tého neuronu \(W_{0}{k}).

Vícevrstvou NS tvoří vždy minimálně tři vrstvy, přičemž mezi dvěma sousedními vrstvami se nachází tzv. úplné propojení neuronů, které znamená, že každý neuron nižší vrstvy je propojen se všemi neurony vrstvy vyšší.


obr. 1: Vícevrstvá neuronová síť
zdroj: VOLNÁ, Eva. Neuronové sítě 1. 2 vyd. Ostrava: Ostravská univerzita v Ostravě, 2008, 87 s. Dostupné také z: https://web.osu.cz/~Volna/Neuronove_site_skripta.pdf.

Problémy modelu vícevrstvé NS s Backpropagation

Minimalizace chybové funkce
Volby vhodné topologie sítě
- volba vhodného počtu neuronů ve vnitřních vrstvách
- volba počtu vrstev (většinou 1-2 vrstvy)
příliš malá síť s algoritmem BP skončí v mělkém lokálním minimu (je třeba doplnit další neurony)
Složitější architektura může vést naopak k přeučení (špatné generalizaci)

Algoritmus BACKPROPAGATION

Jak již bylo řečeno, tento algoritmus je využíván v přibližně 80 % všech aplikací NS. Algoritmus obsahuje 3 etapy:

feedforward (dopředné) šíření vstupního signálu treninkového vzoru
zpětné šíření chyby
aktualizaci váhových hodnot na spojeních mezi neurony

Během první fáze obdrží každý neuron ve vstupní vrstvě $X_i, i = 1, ..., n$ signál/vstup $x_i$ a zařídí jeho přenos ke všem neuronům skryté vrstvy $Z_1, ..., Z_p$. Každý neuron ve skryté vrstvě vypočítá svou aktivaci $z_j$ a předá tento signál neuronům ve vrstvě výstupní. Každý neuron ve výstupní vrstvě spočítá také svoji aktivaci $y_k$ - odpovídá skutečnému výstupu (k-tého neuronu) po předložení vstupního vzoru. Tímto vznikne zpětná vazba a je nutná adaptace NS - aktualizace vah.

Vzorec algoritmu BP a odvození: \[\frac{\delta E}{\delta w_{ij}} = \frac{\delta E}{\delta y_i} \centerdot \frac{\delta y_i}{\delta \varphi_i} \centerdot \frac{\delta \varphi_i}{\delta w_{ij}}\]

to odpovídá následujícímu vzorci:

\[\frac{\delta E}{\delta w_{ij}} = -(d_i - y_i) \centerdot y_i(1 - y_i) \centerdot x_j\]

$y_i(1 - y_i)$ je derivací aktivační funkce - sigmoidy
$(d_i - y_i)$ rozdíl mezi požadovaným výstupem $d_i$ a reálným výstupem $y_i$
$x_j$ je vstup
$-(d_i - y_i) \centerdot y_i(1 - y_i) \centerdot x_j$ $\iff$ chyba připadající na i-tý neuron $\iff$ $\delta_i$

Gradientní metoda a Delta pravidlo - aktualizace vah

Pro optimalizaci vah a minimalizaci chybové funkce se využívá tzv. gradientní metody (také viz. GRADIENT a LOKÁLNÍ MINIMUM v otázce č. 14 - Učení neuronové sítě).


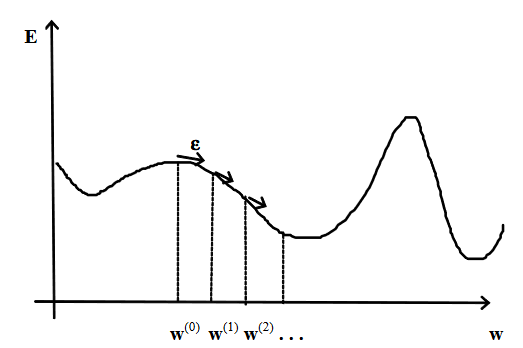obr. 2: Gradientní metoda
zdroj: VOLNÁ, Eva. Neuronové sítě 1. 2 vyd. Ostrava: Ostravská univerzita v Ostravě, 2008, 87 s. Dostupné také z: https://web.osu.cz/~Volna/Neuronove_site_skripta.pdf.

Vertikální osa $E$ nám zachycuje chybovou funkci, která určuje chybu sítě vzhledem k pevné tréninkové množině a v závislosti na konfiguraci sítě. Hledáme konfiguraci vah $w$, při které je chybovost minimální.

Na ose $x$ máme znázorněn mnohorozměrný vektor vah $w$.

náhodně zvolíme konfiguraci sítě v bodě $w^0$ - chybovost je velká
v tomto bodě sestrojíme tečný vektor (GRADIENT)
posuneme se po tomto vektoru dolů o vzdálenost $\varepsilon$
získáme novou konfiguraci $w^1$ = $w^0 + \Delta w^1$, pro kterou je chybovost menší
opakujeme dokud se nedostaneme do lokálního (ideálně globálního) minima

\[\Delta w = - \eta \nabla E\]

$\eta$: (eta) rychlost učení <0, 1>

Delta pravidlo

\[\Delta w_{ij} (t) = \eta * \delta_i (t) x_j + \alpha \Delta w_{ij} (t-1)\]

$\Delta w_{ij}$: změna vah mezi i-tým a j-tým neuronem
$\eta$: (eta) rychlost učení <0, 1>
$\delta_i$: připadající na i-tý neuron
$x_j$: j-tý vstup neuronu
$\alpha$: (alfa) moment/setrvačnost <0, 1)

Parametr $\alpha$ nám udává jakou měrou se má do změny váhy započítat změna předchozí. Změna váhy má dvě složky:

chybu odezvy sítě, započítávající se koeficientem rychlosti učení
předchozí změnu váhy

Pokud je změna váhy malá, dominuje složka chyby sítě. Pokud je tomu obráceně a chyba sítě klesne, je váha stále upravována ve velikosti předchozí změny. Setrvačnost může pomoci dostat se z lokálního minima a nalézt lepší konfiguraci vah s menší chybou.

Parametr $\eta$ určuje o kolik se má upravit váha neuronu (relativně k velikosti chyby). Čím větší koeficient, tím rychleji se síť učí. Nicméně, příliš vysoká hodnota může vést k oscilacím a ideálního řešení nemusí být dosaženo.

Zpětná propagace chyb do skrytých vrstev

\[\delta_i = y_i (1 - y_i) \sum^N_{k-1} w_{ki} \delta_k\]

$N$: počet neuronů v následující vrstvě, tedy vrstvě blíže k výstupu
$\delta_k$: dle předchozí logiky by se mělo jednat o chybovost k-tého neuronu (tedy neuronu skryté vrstvy) - pokud bychom to převedli na obrázek č. 1, tak se jedná o chybovost j-tého neuronu Z

Průběh chyby během učení


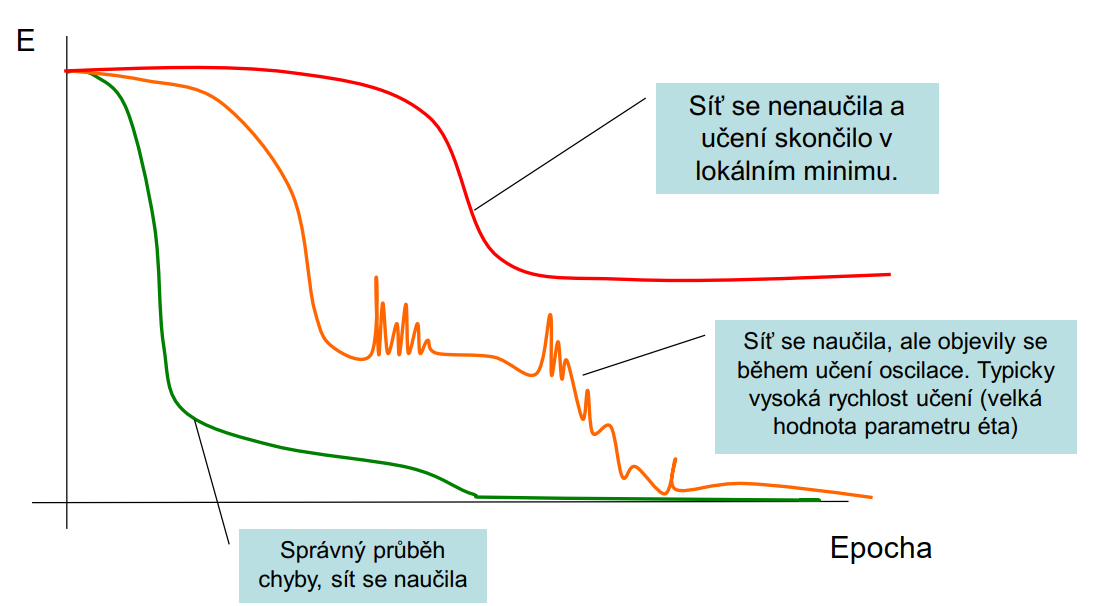obr. 3: Průběh chyby během učení
zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.

ZDROJE

SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.
VOLNÁ, Eva. Neuronové sítě 1. 2 vyd. Ostrava: Ostravská univerzita v Ostravě, 2008, 87 s. Dostupné také z: https://web.osu.cz/~Volna/Neuronove_site_skripta.pdf.
OLEJ, Vladimír a Hájek PETR. Úvod do umělé inteligence: Moderní přístupy - Distanční opora. Univerzita Pardubice: Fakulta Ekonomicko-správní, 2010, 95 s. ISBN 978-80-7395-307-2.

Učení bez učitele

Samoorganizující se neuronové sítě (SOM - Self-Organizing Map)

Tato NS byla poprvé popsána v roce 1982 finským vědcem Teuvo Kohonenem, proto se jí rovněž říká Kohonenova síť. Jedná se o základní princip soutěžního učení, tj. učení bez učitele.

Jedná se o dvouvrstvou síť s úplným propojením neuronů mezi vrstvami (více viz Struktura).

Princip

Vytvoření množiny reprezentantů mající stejné pravděpodobnosti výběru - vybereme-li náhodný input vektor z rozdělení pravděpodobnosti odpovídající rozdělení tréninkové množiny, bude mít každý takový reprezentant přiřazenu takovou pravděpodobnost, která je mu nejblíže.

De facto provádíme shlukovou analýzu, ale nemusíme znát dopředu počet shluků (u K-MEANS je znát musíme).

Váhy se adaptují na základě statistických vlastností trénovací množiny: jsou-li si dva vzory na vstupu blízké, způsobí odezvu na fyzicky si blízkých neuronech, ve výstupní množině.

Cílem je zobrazit mnohodimenzionální data v mnohem jednodušším prostoru.

Struktura sítě

Lineární uspořádání (řetízek) - (vzdálenost mezi neurony je 1)
Čtvercová mřížka (vzdálenost rovnoběžně 1, diagonálně 2 Manhattanská vzdálenost, nebo $\sqrt{2}$ eukleidovská)
Hexagonální mřížka (vzdálenost mezi neurony je 1 ve všech směrech)
Toroid mřížka (vzdálenost rovnoběžně 1, diagonálně 2 Manhattanská vzdálenost, nebo $\sqrt{2}$ eukleidovská)


obr. 1: Jednotlivé topologie SOM
zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.

Nejčastějším typem topologie SOM je Lineární a nebo dvojrozměrná mřížka. Topologie určuje, které neurony spolu sousedí - toto je důležité pro adaptační proces.

Proces učení

\[y_i = \sum_{j=1}^{N} (x_j - w_{ij})^2\]

Vybavování

Předložíme vzor na vstup/vstupní vrstvu a vypočteme odezvy. Neuron s nejmenší odezvou (reprezentant) je vítězný neuron a reprezentuje shluk, kam vzor patří.

Učení

Vezmeme vítěze a jeho váhy posuneme o kousek blíže k učenému vektoru. Kromě vítěze upravujeme váhy i sousedních neuronů - čím dále tím méně upravujeme. Postup opakujeme do $\alpha (t)$ = 0.

\[\Delta w_{ij} = \alpha (t) (x_j - w_{ij}) (h(i, b))\]

$\alpha (t)$: rychlost učení, proměnná v čase, jež klesá do nuly
funkce $h(i, b)$ je maximální, pokud i je indexem vítězného neuronu $(i = b)$, pokud je to jiný neuron, tak funkce h klesá v závislosti na vzdálenosti od vítězného neuronu.

Extrémní je hodnota 1 pro $(b = i)$, jinak 0.


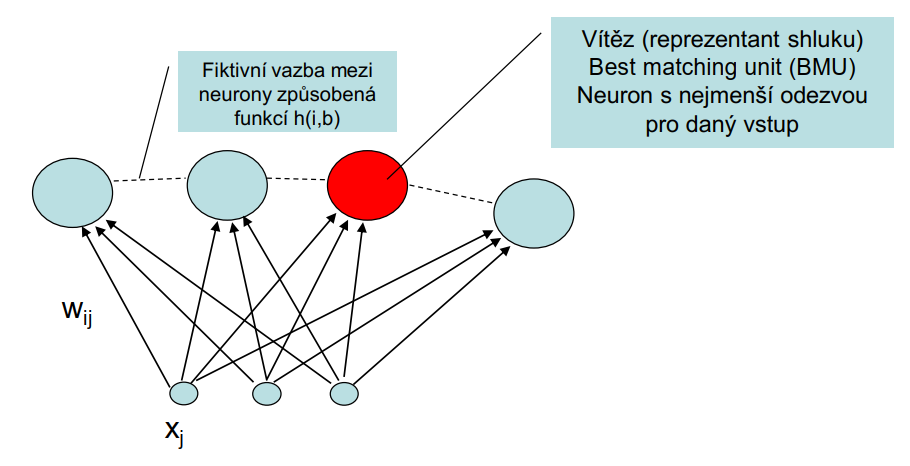obr. 2: Popis struktury SOM
zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.


obr. 3: Vizualizace shlukování v rámci SOM
zdroj: Trénování samoorganizující sítě. In: , Chompinha. Wikipedie Otevřená Encyklopedie [online]. Wikimedia Commons, 2019 [cit. 2023-05-09]. Dostupné z: https://cs.wikipedia.org/wiki/Samoorganizuj%C3%ADc%C3%AD_s%C3%AD%C5%A5#/media/Soubor:TrainSOM.gif

Funkce $h (i, b)$

Tato funkce nám určuje, jak se budou měnit váhy neuronů blízkých vítěznému neuronu $\Rightarrow$ Jak se budou prototypy reprezentované neurony posouvat směrem k učenému vzoru. Nejvíce bude přitahován vítězný neuron a nejméně neuron, který je od vítězného nejdále.

Pokud je funkce $h (i, b)$ záporná, tak jsou neurony odpuzovány, je-li kladná, jsou přitahovány, takto se tvoří shluky.


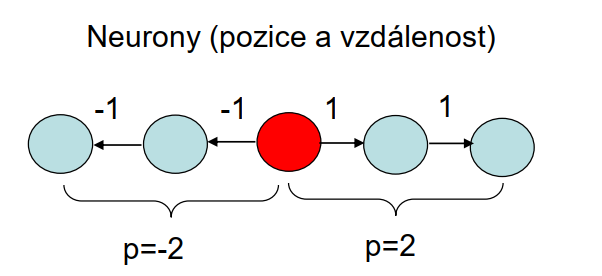obr. 4: Vzdálenost a neurony
zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.

Při učení se začíná s plochou $h (i, b)$, která postupně nabývá strmější charakter "Mexický klobouk, viz obrázek níže.


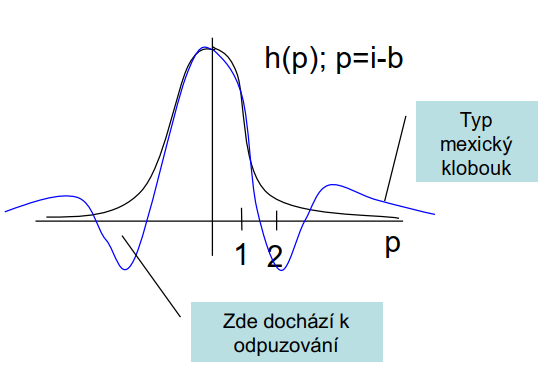obr. 5: Průběh funkce h (i, b)
zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.

Jinými slovy, vítězný neuron a jeho nejbližší sousedé budou měnit váhový vektor o poměrnou vzdálenost směrem k aktuálnímu vstupu. Cílem je, aby vítězný neuron, který se nejvíce podobá vstupnímu vektoru/vzoru ještě více zlepšil svoji relativní pozici vůči tomuto vstupu. Problémem v průběhu adaptace může být nevhodná náhodná inicializace počátečních vah. Toto vede následně ke změnám směrem k počátečním neuronům ve výstupní vrstvě a tedy pouze jeden z těchto neuronů vyhraje kompetici (soutěž) a zbytek neuronů je nevyužit.

V aktivním režimu to funguje tak, že nejbližší neuron vstupnímu vzoru je excitován na hodnotu 1 a zbylé neurony na hodnotu 0. Excitovaný neuron je navíc schopen rozpoznat celou třídy podobných vzorů/vektorů. Tento princip Vítěz bere vše je realizován tzv. Laterální inhibicí - tj. všechny výstupní neurony jsou propojeny laterálními vazbami přenášejícími inhibiční signály.

Každý neuron se následně snaží oslabit ty sousední, a to silou úměrnou jeho potenciálu (blíže vstupu se potenciál zvyšuje).

Výsledek je, že výstupní neuron s největším potenciálem utlumí všechny ostatní neurony a sám zůstane aktivní.

Algoritmus SOM

Inicializujeme váhy neuronů náhodnými hodnotami a nastavíme počáteční hodnotu koeficientu α(t).
Vybereme vektor z učící množiny a přiložíme na vstup sítě.
Vypočteme výstupy neuronů $y_i$.
Zjistíme neuron s nejmenší odezvou - reprezentant.
Pro každý neuron upravíme váhu o $\Delta {w_ij}$.
Dokud nevyčerpáme učící množinu, pokračujeme bodem 2.
Snížíme koeficient $\alpha (t)$, dokud je $\alpha (t) > 0$, tak pokračujeme bodem 2, od počátku učící množiny.

U-Matice

Zachycuje odezvu SOM. Barva neuronů v hexagonální mřížce nám indikuje průměrnou vzdálenost vah daného neuronu od jeho sousedů. Na obrázku níže jsou bíle zachyceny neurony s podobnými vahami - tvoří shluky - zatímco tmavá políčka nám shluky oddělují (neurony mají zcela jiné váhy).


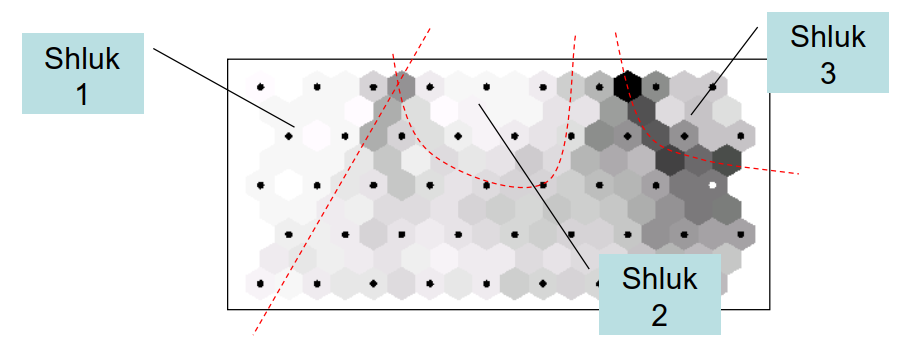obr. 6: U-Matice
zdroj: HOLLMEN, Jaakko. U-matrix representation of the Self-Organizing Map. In: Jaakko Hollmén's Research Home Page [online]. Aalto University School of Science: Jaakko Hollmén, 1996 [cit. 2023-05-09]. Dostupné z: http://users.ics.aalto.fi/jhollmen/dippa/node24.html

ZDROJE

SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.
VOLNÁ, Eva. EVOLUČNÍ ALGORITMY A NEURONOVÉ SÍTĚ: URČENO PRO VZDĚLÁVÁNÍ V AKREDITOVANÝCH STUDIJNÍCH PROGRAMECH. Ostravská univerzita v Ostravě, 2012, 152 s. Dostupné také z: http://physics.ujep.cz/~mmaly/vyuka/MPVT_II/Heuristiky/SOMAdetail-Evolucni_algoritmy_a_neuronove_site+Genetika.pdf

Rekurentní neuronové sítě

Fuzzy množina a fuzzy logika

funkce příslušnosti, fuzzy pravidla, fuzzyfikace, inference a defuzzyfikace

Fuzzy logika vs tradiční logika

V klasické logice máme pouze dva stavy: 1 nebo 0, true nebo false. Ve fuzzy logice je stav interpretován na stupnici od 0 do 1. Stav může být tedy například 0,3, 0,7 nebo 1 -> může být neurčitý.

Ale stav čeho?

Funkce příslušnosti

Definice: reprezentuje úroveň pravdivosti určité vlastnosti

Vlastnost se vztahuje k zkoumané veličině. Zkoumanou veličinou může být například teplota. Jaká může být teplota? Může být teplo, chladno, nebo tak nějak normálně. Nebo to může být vzdálenost. Jsme blízko, daleko, středně daleko. Nebo i riziko půjčky klientovi. Velké, střední, malé. Tradiční logika je na vše z toho schopná odpověď jen ano, nebo ne. Riziko půjčky? - ano/ne. Teplota - ano, je teplo; ne, není teplo. Vzdálenost - ano, jsme blízko; ne, jsme daleko.

Na obrázku pod je uveden příklad funkce příslušnosti pro vlastnost chladno. Nebo třeba vlastnost pomalu pokud se fuzzy systémem snažíme řídit rychlost. Pro účely této otázky budeme řídit teplotu v domácnosti.


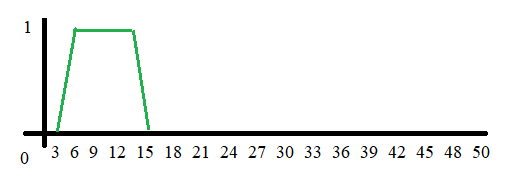obr. 1: Funkce příslušnosti. Na ose `x` jsou vstupní hodnoty a na ose `y` úroveň pravdivosti
Vlastní zdroj

Funkcí pravdivosti můžeme mít i více -> v závislosti na tom, kterou veličinu fuzzyfikujeme. Naše teplota má 3 funkce pravdivosti.


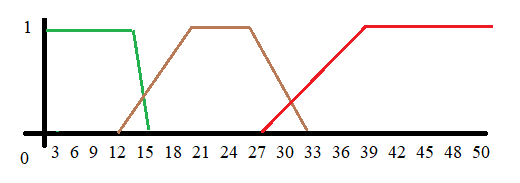obr. 2: 3 funkcí příslušnosti pro veličinu teplota: `chladno` - zelená, `normálně` - hnědá, `horko` - červená
Vlastní zdroj

Můžeme se na to koukat následovně:

Když je 6 stupňů, tak je zima, jakmile se dostaneme na 12 stupňů, tak už přestává být zima a začíná být normálně, normálně je na 21 stupňů. Jak se blížíme k 30 stupňům, přestává být normálně a začíná být horko a vše nad 39 stupňů už je horko.

Ale jak jsme přišli na tyhle hodnoty? Vymyslely jsme si je. V reálném světe se používají expertní fuzzy systémy.

Jsou to fuzzy systémy, ve kterých experti na daný obor určili, jaké hodnoty daná funkce příslušnosti pokrývá. Jednotlivé prvky množiny vstupních hodnot mají povětšinou strukturu typu "Když je hodnota taková, tak patří do téhle funkce příslušnosti" (například: když je hodnota 3, tak je chladno).
K fuzyfikaci se vztahují problémy tzv. přechodů. Tedy například je třeba rozhodnout, s jakou mírou pravdivosti je pravda, že když je hodnota 14, tak je chladno. Ze vstupní množiny je třeba tím pádem také rozpoznat, v jakých hodnotách se tyto přechody nacházejí.

Ale k čemu nám to je?

Fuzzyfikace

Umožní nám vzít vstup do systému a přeměnit ho na set, jež obsahuje míru pravdivosti se kterou se vstupní hodnota vztahuje k funkcím příslušnosti.

Definice: jedná se o proces přeměny vstupní hodnoty na fuzzy množinu

Řekněme, že našim naměřeným vstupem je 27 stupňů. Výstupem fuzzyfikace je poté set, který obsahuje hodnoty toho, jak moc hodnota 27 odpovídá jednotlivým funkcím příslušnosti. Pro 27 stupňů je to tedy [0; 0,7; 0,2].

Vstupní hodnota je nyní fuzzyfikovaná, tuto hodnotu, využijeme při inferenci.

Inference a fuzzy pravidla

Jedná se o proces vyhodnocování vstupů do našeho fuzzy systému, za pomocí setu fuzzy pravidel.

Fuzzy pravidla si určujeme při návrhu systému (nebo je upravíme později) a mají následující strukturu:

IF teplota IS chladno THEN klimatizace IS vypnuta.

Toto byl jen příklad pravidla, povětšinou máme celý set, který se vyhodnocuje najednou. Pro náš příklad si vytvoříme tento set:

IF teplota IS chladno THEN klimatizace IS vypnuta
IF teplota IS normální THEN klimatizace IS málo
IF teplota IS horko THEN klimatizace IS hodně

Můžeme si všimnout, že najednou tu máme jakousi klimatizaci a její vlastní množinu funkcí příslušnosti. Je to kvůli dalšímu kroku, defuzzyfikaci, která ním umožní určit výstup systému.

Každé fuzzy pravidlo nám vrátí hodnotu. V našem jednoduchém případě, kdy má každé pravidlo jen jednu podmínku (žádné AND nebo OR), tak je jednoduché je vyhodnotit. Výstupem je další set, obsahující míry pravdivostní, tentokrát však pro pravou stranu pravidel, tedy pro klimatizaci a její funkce příslušnosti.

Protože se jedná o velmi jednoduchý příklad, tak tento set má opět tvar [0; 0,7; 0,2]. Toto se moc často neděje, povětšinou jsou fuzzy pravidla složitější a výsledek inference se značně liší od vstupu.

Defuzzyfikace

Tento krok se zabývá převedením setu mír příslušností (fuzzy množiny) získaného skrze inferenci na číslo. Pro defuzzyfikaci máme vlastní funkce příslušnosti, v našem případě jde o rychlost otáček větráku klimatizace v procentech.


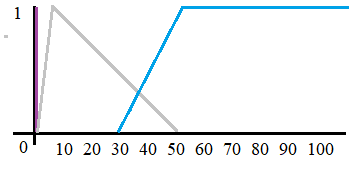obr. 3: 3 funkce příslušnosti pro veličinu klimatizace: `vypnuto` - fialová, `málo` - šedá, `horko` - modrá
Vlastní zdroj

Našim úkolem je nyní namapovat hodnoty získané skrze inferenci tak, abychom dostali výstupní hodnotu, která nám bude říkat, jak se má výsledný řízený systém chovat.

Je spoustu způsobů, jak toto provést, ale populárním a používaným způsobem je oseknout funkce příslušnosti podle získané fuzzy množiny a spočítat střed nově vzniklého útvaru.

Defuzzyfikace podle naši fuzzy množiny vypadá následovně:


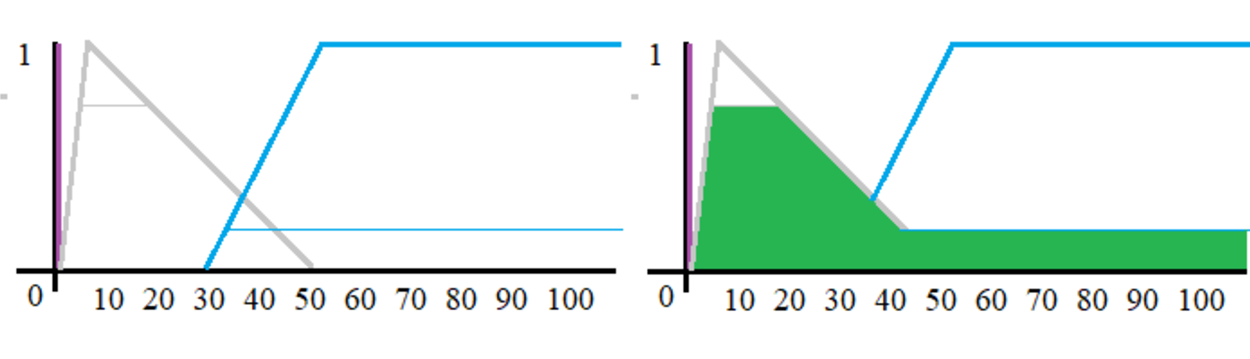obr. 4: Určení limitu pro oseknutí - vlevo a výsledný útvar, jehož střed je výsledkem - vpravo
Vlastní zdroj

Výsledkem je, že při teplotě 27 stupňů budou otáčky klimatizace cca 30%.

Defuzzyfikace, je narozdíl od fuzzyfikace výpočetně náročnější, hlavně díky kroku převádění fuzzy množiny na číslo.

Celý proces by se dal popsat jako mapování vstupních veličin na výstupní veličiny.


obr. 5: Schéma systému s přidanou zpětnou vazbou
Dostupné z: https://www.researchgate.net/figure/Architecture-of-fuzzy-logic-control_fig1_337511172

Výhody fuzzy logiky oproti IF tvrzení

Jeden by si mohl říct, že je stejná věc by se dala udělat i přes pár IFů v Javě. Koneckonců, fuzzy pravidla jsou také IF tvrzení.

IF tvrzení se stanou ve složitějších případech až příliš komplikovaná, zde byl uvedený příklad s jedním vstupním parametrem (teplota) v případě více vstupních parametrů jsou jednotlivé závislosti mnohem složitější na modelaci pomoci IF tvrzení (například modelování závislosti dýška v restauraci na základě kvality jídla a kvality obsluhy).
Fuzzy pravidla jsou modulární, můžeme je lehce upravit a přizpůsobit tak systém změnám v budoucnu.
Nemusíme znát podrobně celý systém, pro který fuzzy pravidla vytváříme. Stačí nám vědět, co chceme řídit. Návrh fuzzy systému můžeme klidně začít od inferenční části.

Využití

Fuzzy systémy se dají využít k nepřebernému množství úkonů, hlavně díky tomu, že umí pracovat s neurčitostí.

řízení systému v reálném čase (náš příklad)
modelování závislostí
zpracování obrazu (získání kontur, kdy zjišťujeme, jestli pozice linek vůči sobě odpovídá danému natočení)
rozpoznávání hlasu
a hodně dalších, dostupných například zde

Zdroje

Fuzzy logic. Wikipedia: The Free Encyclopedia [online] @2023 citováno [17.05.2023]
Dostupné z: https://en.wikipedia.org/wiki/Fuzzy_logic
Difference between Fuzzification and Defuzzification. GeeksForGeeks [online] @2023 citováno [17.05.2023]
Dostupné z: https://www.geeksforgeeks.org/difference-between-fuzzification-and-defuzzification/
An Introduction to Fuzzy Logic. Tim Arnett [online] @2015 citováno [17.05.2023]
Dostupné z: https://www.youtube.com/watch?v=rln_kZbYaWc
What Is Fuzzy Logic?. Matlab [online] @2022 citováno [17.05.2023]
Dostupné z: https://www.youtube.com/watch?v=__0nZuG4sTw
Fuzzy Logic - Computerphile. Computerphile [online] @2014 citováno [17.05.2023]
Dostupné z: https://www.youtube.com/watch?v=r804UF8Ia4c

Genetický algoritmus

princip, základní pojmy

Genetický algoritmus je heuristická optimalizační metoda, řadící se mezi tzv. evoluční algoritmy, inspirovaná přirozeným výběrem živočišných druhů, tj. evoluční biologií, užívaná k řešení složitých optimalizačních úloh. Existuje velké množství algoritmů, které lze označit za genetické algoritmy.

Co je to evoluční algoritmus?

V přírodě biologičtí jedinci jedné populace mezi sebou soutěží o přežití a možnost reprodukce na základě toho, jak dobře jsou přizpůsobeni prostředí. V průběhu mnoha generací se struktura dané populace vyvíjí na základě Darwinovy teorie o přirozeném výběru a přežívání jen těch jedinců, kteří mají největší sílu (schopnost přežít).

Evoluční algoritmy se snaží využít modelů evolučních procesů, aby tak nalezly řešení náročných a rozsáhlých úloh. Veškeré takové modely mají několik společných rysů:

pracují zároveň s celou skupinou (množinou) možných řešení zadaného problému místo hledání jednotlivého řešení
vygenerovaná řešení postupně vylepšují zařazováním nových řešení, získaných kombinací původních
kombinace řešení jsou následovány náhodnými změnami a vyřazováním nevýhodných řešení

Genetický algoritmus - pojmy

Populace
- soubor jedinců
- na začátku máme soubor, jež se nazývá výchozí populace
Jedinec
- člen populace popsaný chromozomem
- potenciální řešení optimalizační úlohy
Chromozom
- řetězec nezávisle proměnných optimalizované funkce, neboli řešení optimalizační úlohy (stavební plán jedince), chromozom jedince nemusí být nejlepší řešení optimalizační úlohy
- chromozom některého jedince může vypadat následovně: (1, 0, 1, 0, 1, 1, 0, 0)
Fitness funkce
- optimalizovaná funkce (ohodnocení schopnosti jedince přežít v okolním prostředí)
- fitness funkce může být dána například počtem 1 v chromozomu
Generace
- soubor řetězců nezávisle proměnných optimalizované funkce (jedinců) "stejného věku"
- například tedy platí, že Výchozí populace je nultá generace
Reprodukce
- tvorba nové generace jedinců pomocí křížení a mutace jedinců staré generace
- jedinci s nejvyšší fitness funkcí vytvářejí nového potomka
Křížení
- výměna podřetězců nezávisle proměnných optimalizované funkce mezi dvěma řetězci (výměna genetické informace)
- spojení chromozomu dvou rodičů
- nový jedinec bude mít chromozom vytvořený z částí chromozomů jeho rodičů
Mutace
- přepsání podřetězce nezávisle proměnných optimalizované funkce (poškození genetické informace)
- dá se implementovat jako náhodná změna v chromozomu jedince
- neděje se tak často, jako křížení

Princip genetického algoritmu

Princip genetického algoritmu je postupná tvorba na sebe navazujících generací různých řešení optimalizační úlohy vždy o stejném počtu jedinců. Jak populace probíhá evolucí (střídání generací), řešení se zlepšují. Tradičně je řešení reprezentováno řetězcem celých nebo binárních čísel.

První generace je na začátku algoritmu složena z náhodně vygenerovaných jedinců. Během přechodu od předchozí generace (rodičů) k následující generaci (potomků) jsou jedinci předchozí generace pomocí křížení a mutací reprodukováni v modifikované jedince následující generace. Tento postup se iterativně opakuje. Nejjednodušší verze tohoto algoritmu starou generaci zahazuje a pracuje jen s tou novou.

Existuje velké množství způsobů - algoritmů, kterými lze tento princip uplatnit.

Příklad algoritmu

Mějme první generaci tvořenou množinou náhodně vygenerovaných řetězců (bajtů) jako množinu čtyř individuí reprezentovaných chromozomem délky 8.

(1, 0, 1, 0, 1, 1, 0, 0)
(0, 1, 1, 1, 1, 1, 0, 1)
(0, 0, 0, 1, 0, 0, 0, 1)
(1, 1, 0, 0, 1, 1, 0, 0)

Poté je třeba jedince ohodnotit pomocí fitness funkce. Definice této funkce je dána konkrétním problémem kde se snažíme najít jedince, jež mají z hlediska našeho problému optimální vlastnosti. Řekněme že naše definice je počet 1 v chromozomu jedince.


obr. 1: Ohodnocení jedinců
dostupné z: https://cs.wikipedia.org/wiki/Genetick%C3%BD_algoritmus

Další následuje výběr rodičů, kteří se budou podílet na nové generaci. Výběr rodičů by měl respektovat pravidla přirozeného výběru dle Darwinovy teorie o původu druhů. To znamená, že zdatnější jedinci mají větší šanci se prosadit v konkurenci jiných, lépe překonávat překážky a žít déle. Jedinci s vyšším ohodnocením mají větší pravděpodobnost výběru partnera.

Výběr probíhá povětšinou náhodně s tím, že jedinec s vyšší hodnotou fitness má větší šanci na to být vybraný.


obr. 2: Vybraní rodiče
dostupné z: https://cs.wikipedia.org/wiki/Genetick%C3%BD_algoritmus

Nyní následuje reprodukce, tedy vytváření jedinců nových, za pomocí křížení. Existuje spousty technik křížení, ale tady si ukážeme tzv jednobodové křížení. Každému páru vybereme bod a nový jedinec dostane levou část jednoho rodiče, a pravou část druhého.


obr. 3: Výsledek křížení
dostupné z: https://cs.wikipedia.org/wiki/Genetick%C3%BD_algoritmus

Nové chromozomy reprezentují další generaci.

Na novou generaci je možnost aplikovat mutaci. Dává se většinou malá šance (v řádech setin procent) že se mutace aplikuje, aby populace nezdegradovala. Mutace totiž změní v každém chromozomu náhodně jednu hodnotu.


obr. 4: Výsledek mutace na nové generaci
dostupné z: https://cs.wikipedia.org/wiki/Genetick%C3%BD_algoritmus

Nyní se vrátíme do kroku jedna, tedy znovu ohodnotíme jedince, vybereme rodiče a provedeme reprodukci. Toto se může dít tak dlouho, dokud se nám neobjeví optimální jedinec, nebo alespoň téměř optimální, nebo dokud změna fitness funkce skrze několik generací nebude blízká 0. Účelem je mít po konečném počtu generací jedince s co nejlepší fitness funkcí.

Příklady aplikace genetických algoritmů

nejpoužívanější jsou pro optimalizační úlohy (např. plánování, navrhování obvodů VLSI) a pro strojové učení (klasifikace, predikce, učení neuronových sítí)
byly použity pro "automatické programování" (např. vývoj buněčných automatů, genetické programování)
chemie (určování struktury složitých molekul)
ekonomie (predikce, hledání parametrů ekonomických modelů)
biologie a medicína (modelování imunitního systému, modelování ekologického systému)
sociologie (modelování sociálního systému)

Zdroje

Petr Luner. Jemný úvod do genetických algoritmů. [online]. @2022 [cit. 2023-04-24].
Dostupné z: https://cgg.mff.cuni.cz/~pepca/prg022/luner.html
Wikipedie - Otevřená encyklopedie. Genetický algoritmus. [online]. @2023 [cit. 2023-04-24].
Dostupné z: https://cs.wikipedia.org/wiki/Genetick%C3%BD_algoritmus
Marek Obitko. Genetické algoritmy: Matrice života v počítačích. [online]. @2001 [cit. 2023-04-24].
Dostupné z: https://www.scienceworld.cz/technologie/geneticky-algoritmus-matrice-zivota-v-pocitacich-4530/

Přírodou inspirované optimalizační algoritmy a jejich principy

Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO)

Úvod

Jedná se o sadu algoritmů, imitujících chování přírodních situací. Tedy imitujících chování například zvířat, chemických procesů nebo biologie.

Tyto algoritmy můžeme dělit na dva druhy

stochastické: Také se jím říká náhodné. Pokud algoritmus vykazuje jakékoliv známky nahodilosti, jedná se o stochastický typ.
deterministické: Neobsahují nahodilost, můžeme předem určit výsledek.

Obecně lze princip Přírodou inspirovaných optimalizačních algoritmů rozdělit na 4 části:

Identifikace parametrů populace
- Náhodně vytvoříme iniciální populaci tak, aby pokryla co největší prostor řešení (cíl optimalizační úlohy). Velikost populace je dána tím, jakou optimalizační úlohy chceme řešit (velikost populace je jeden z parametrů).
Výpočet parametrů populace
- Zjistíme, zdali parametry vybrané v první částí jsou dostatečné ke splnění cíle.
V této fázi se mění jednotlivé proměnné tak, aby bylo dosaženo toho, že systém je kontrolovaný. Jak se mění parametry, celý systém se přizpůsobuje a aktualizuje směrem k dosažení cíle (pokud samozřejmě měníme parametry dobře).
- Příklad: Umělá kolonie včel bude mít parametry jako jsou zaměstnané včely, kritérium pro opuštění a včelí zvědi. Výběr zdroje jídla a samotný zdroj jídla jsou poté proměnné. Pří výkonu algoritmu upravujeme tyto proměnné.
Výsledek algoritmu je vyhodnocen. V případě nesplnění cílů optimalizace je možné upravit parametry a začít znovu.


obr. 1: Obecný princip přírodou inspirovaných optimalizačních algoritmů
Převzato z: https://www.tutorialspoint.com/how-to-convert-regular-expression-to-finite-automata

Particle Swarm Optimization (PSO)

Princip algoritmu je založený na hejnech živočichů, například ptáků. Jedinec tohoto hejna těží z vlastností ostatních jedinců, například při vyhledávání potravy nebo při letu (hejno se pohybuje najednou).

Můžeme si představit, že každý jedinec (particle) hejna (swarm) nám může pomoci najít optimální řešení. Řešení nalezené celým hejnem je poté nejlepším optimálním řešením.

Využití tohoto algoritmu je k nalezení globálního minima.

Princip

Řekněme, že máme nějaký prostor, ve kterém hledáme optimální řešení. V našem případě je tímto optimálním řešením globální minimum nějaké funkce.

Problémem je, že minimum, které nalezneme, nemusí být globální minimum, neb prostor obsahuje lokální minima.

Algoritmus řeší problém pomocí populace částic. Tyto částice jsou prvně rozmístěny náhodně skrz celý prostor popsaný funkcí. Každá tato částice se pohybuje na základě její rychlosti a nejlepšího řešení, které doposud nalezla.

Jedna částice je tedy schopná najít nějaké minimum, ale nemáme žádnou možnost říct, zdali jde o globální minimum.

Jednotlivé částice jsou spolu propojené a sdílí informace o nalezených hodnotách. Pokud nějaký člen hejna / částice najde hodnotu odpovídající lokálnímu minimu, je tato hodnota předána ostatním částicím. Pokud je tato hodnota výhodnější, nežli ta, kterou částice jiná našla, částice to zohlední při směru cesty. Nepostupuje však přímo, dělá tak s jistou odchylkou, protože je možnost, že na své cestě najde ještě více výhodnější hodnotu, kterou poté předá zbytku hejna.

Parametr, který určuje váhu hodnoty nejlepší lokace v řešeném prostoru, musí být menší než 1. Kdyby tomu tak nebylo, tak celé hejno velmi rychle skončí v některém lokálním minimu.

Propojení mezi částicemi může být:

úplné (každá s každou) propojení může vést ke skončení celého hejna v nějakém lokálním minimu
částečné (propojeny jsou pouze subsety částic)

Proměnné tohoto algoritmu jsou hodnoty, které udávají, jakým způsobem se bude částice v prostoru pohybovat.


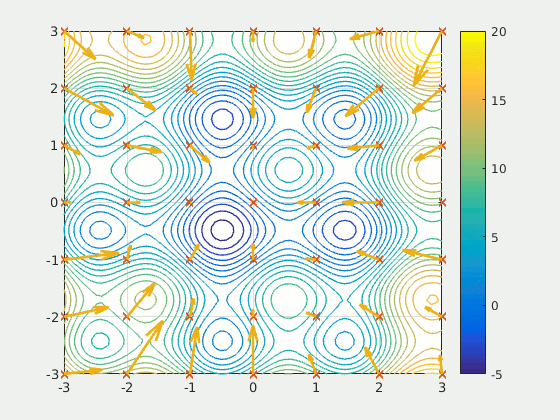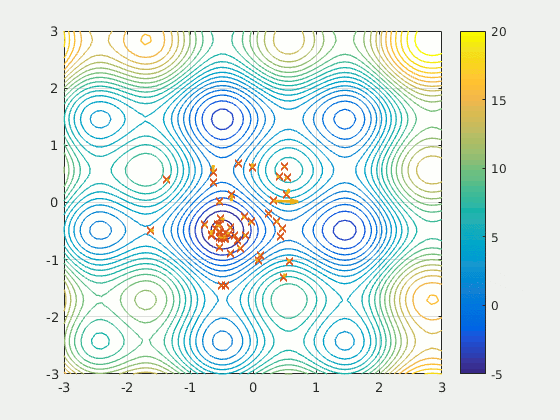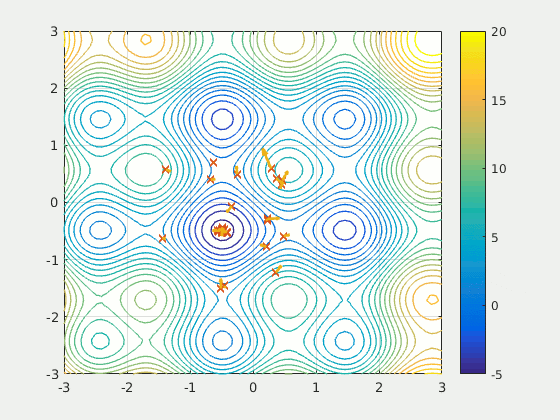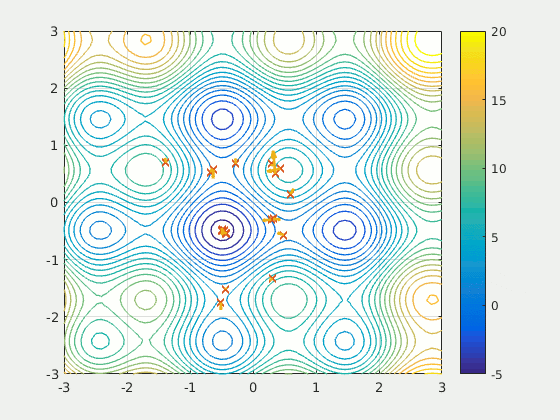obr. 2: Vizualizace PSO algoritmu. Všimněme si, jak některé částice i když znají směr udávaný hejnem, nepostupují přímo a pro jiné nemá hodnota nalezena hejnem takovou váhu, jako je funkce udávající jejich pohyb společně s již nalezeným lokálním minimem.
Převzato z: https://en.wikipedia.org/wiki/Particle_swarm_optimization

Ant Colony Optimization (ACO)

Jedná se o probabilistickou optimalizační techniku, která se zaobírá optimalizačními problémy typu nalezení nejkratší cesty.

Algoritmus je inspirován způsobem, jakým mravenci vyhledávají potravu.

Mravenci náhodně cestují, pokud naleznou potravu, odnášejí ji zpět do mraveniště a značkují tuto cestu pomocí feromonů. Pokud nějaký mravenec nalezne tuto cestu, tak s velkou pravděpodobností přestane náhodně cestovat a vydá se po této cestě a posiluje značkovací feromon -> čím více mravenců po cestě cestuje, tím více se tato cesta zdá jako optimálním řešením.

Avšak, tento feromon po nějaké době vyprchá. Pokud je tedy cesta dlouhá, tak feromon vyprchává rychleji, než ho mravenci stíhají doplňovat a cesta již není tak atraktivní, což umožňuje mravencům opět náhodně cestovat a mít možnost najít kratší cestu, kde bude feromon vyprchávat pomaleji.

Nyní si uvedeme základní algoritmus s rodiny Ant Colony Optimization algoritmů, který se nazývá Ant system.

Princip

Pro aplikování algoritmu je nutné optimalizační problém převést na hledání minimální cesty ve váženém grafu.

Jednotlivé váhy hran mohou odpovídat vzdálenostem mezi uzly, které tyto hrany spojují.

Algoritmus se skládá ze 3 kroků, které jsou v cyklu.

Každý mravenec najde nějaké svoje řešení optimalizační úlohy. Při první iteraci je pravděpodobnost vybrání konkrétní cesty z bodu X do bodu Y stejná pro všechny tyto cesty (hrany). Mravenec tedy najde cíl (jídlo) "náhodou". Cestou pokládá feromon (zvyšuje atraktivitu cesty).
Nyní se musí mravenec vrátit. Cesta s největší atraktivitou má větší probabilitu že bude vybrána. Tedy i ti mravenci, kteří dorazili do cíle po delší cestě, se mohou vrátit kratší cestou -> buď náhodou nebo díky tomu,že je na ni více feromonu (je více atraktivní). Tím, jak se mravenci vracejí, zároveň posilují atraktivitu cesty.
Nyní skončil jeden cyklus a v grafu se nacházejí cesty, s různou atraktivitou. Hodnota atraktivity a všech cestách je nyní aktualizována, aby byl simulován úbytek feromonu. Úbytek feromonu závisí na:

proměnné určující úbytek
délce cesty (delší cesta, větší úbytek)

V dalších iteracích je už více pravděpodobné, že si mravenci vyberou cestu, která obsahuje více feromonu. Mravenec se rozhoduje kudy půjde na základě dvou kritérií:

atraktivita: síla feromonu (tady to voní fakt dobře, tam něco bude)
zkušenost: když jsem šel předtím tudy, tak jsem našel jídlo (cíl úlohy)

Tyto vlastnosti přispívají k pravděpodobnosti, že si mravenec cestu vybere. Je zde tedy vždy možnost, že si mravenec vybere cestu jinou, čímž je možnost, že objeví cestu kratší. Pokud by byla cesta opravdu kratší, mravenec má šanci, že po této cestě půjde znovu i v další iteraci -> zkušenost a bude pokládat feromon -> atraktivita jak pro něj, tak pro potenciální další mravence. Kratší cesta také znamená, že se úbytek feromonu skrz iterace je kratší. Tímto je řešen problém lokálního minima.

Využití tohoto algoritmu se prvně objevilo jako cíl řešení optimalizační úlohy Problém obchodního cestujícího. Dnes se dá využít na optimalizační úlohy, kde nás zajímá nejkratší cesta (síťování, doprava).

Variace algoritmu

Existují další variace, s lehce upraveným postupem, hlavně v oblasti aktualizace feromonu a způsobu výběru cesty jednotlivcem v každé iteraci.

Ant colony system (ACS): Pouze nejlepší mravenec (ten, který nalezl v konkrétní iteraci nejlepší řešení) může aktualizovat váhy pomocí aplikace globálního pravidla pro aktualizaci feromonů.
Elitist ant system: Krom toho, že mravenci posilují atraktivitu cest, tak globálně nejlepší řešení (cesta) si sama vytváří malé množství feromonu, i když po ni žádný mravenec nešel.
Max-min ant system (MMAS): Pouze globálně nejlepší řešení a lokálně nejlepší řešení (nejlepší řešení konkrétní iterace) mohou přidávat feromon a zvyšovat tím svoji atraktivitu. Pro zamezení stagnace je nastavena minimální a maximální hodnota, kterou mohou cesty mít. Na začátku algoritmu je hodnota feromonu na všech cestách maximální.
Rank-based ant system (ASrank): Pouze omezené množství mravenců (x nejlepších řešení v iteraci) může přidat feromon na cesty, kterými prošlo. Kratší cesty mezi uzly získávají více feromonu.
Parallel ant colony optimization (PACO): Mravenci jsou rozděleni do skupin, které jsou schopné se spolu dorozumívat.
a pár dalších...

Zdroje

An Introduction to Nature-inspired Optimization Algorithms (NIOAs). Mobarak Inuwa [online] @2022 [citováno 16.05.2023].
Dostupné z: https://www.analyticsvidhya.com/blog/2022/11/an-introduction-to-nature-inspired-optimization-algorithms-nioas/
Particle swarm optimization. Wikipeida: The Free Encyclopedia [online] @2023 [citováno 16.05.2023].
Dostupné z: https://en.wikipedia.org/wiki/Particle_swarm_optimization
Introduction to Ant Colony Optimization GeeksForGeeks [online] @2021 [citováno 16.05.2023].
Dostupné z: https://www.geeksforgeeks.org/introduction-to-ant-colony-optimization/
Ant colony optimization algorithms. Wikipeida: The Free Encyclopedia [online] @2023 [citováno 16.05.2023].
Dostupné z: https://en.wikipedia.org/wiki/Ant_colony_optimization_algorithms

Hluboké neuronové sítě

Hluboké učení je disciplína v rámci strojového učení, která se zabývá učením neuronových sítí s velkou hloubkou. Hloubkou modelu se myslí počet vrstev neuronů, které jsou za sebou zapojeny tak, že výstup jedné vrstvy je vstupem vrstvy následující. U modelů hlubokého učení se přitom hloubka nachází často v řádech desítek a více vrstev.

Při tréninku hluboké neuronové sítě se váhy mezi neurony upravují tak, aby sítě byly schopné přesněji predikovat výsledky na základě poskytnutých dat. K tomuto účelu se používá metoda zvaná zpětné šíření chyby (backpropagation), která upravuje váhy sítě na základě rozdílu mezi předpovídanými výstupy a správnými výstupy.

Pěkná ukázka funkčnosti hluboké neuronové sítě je znázorněna ve videu (01:34 - 03:00).

Trénování

Proces trénování lze rozdělit (viz obr. 1) na:

Forward propagation - vstupní data jsou předány síti, která vypočítá postupně hodnoty aktivační funkce a výstupy jednotlivých neuronů a pošle je do další vrstvy. Spojení mezi vrstvami funguje prostřednictvím parametrů (váhy a biasy). Tento proces se opakuje až do dosažení výstupní vrstvy, kde se vypočítají predikce.
Výpočet chyby (loss function) - následuje výpočet chyby mezi předpovězenými výstupy sítě a správnými výstupy ze vstupních dat. To poskytuje informaci o tom, jak moc se síť mýlí.
Backpropagation - po výpočtu ztrátové funkce se provádí aktualizace váh a biasů pomoci optimalizačního algoritmu. Cílem optimalizačního algoritmu je najít globální minima, kde má ztrátová funkce minimální hodnotu. Při backpropagation se výpočty provádějí od výstupní vrstvy ke vstupní vrstvě (zprava doleva).


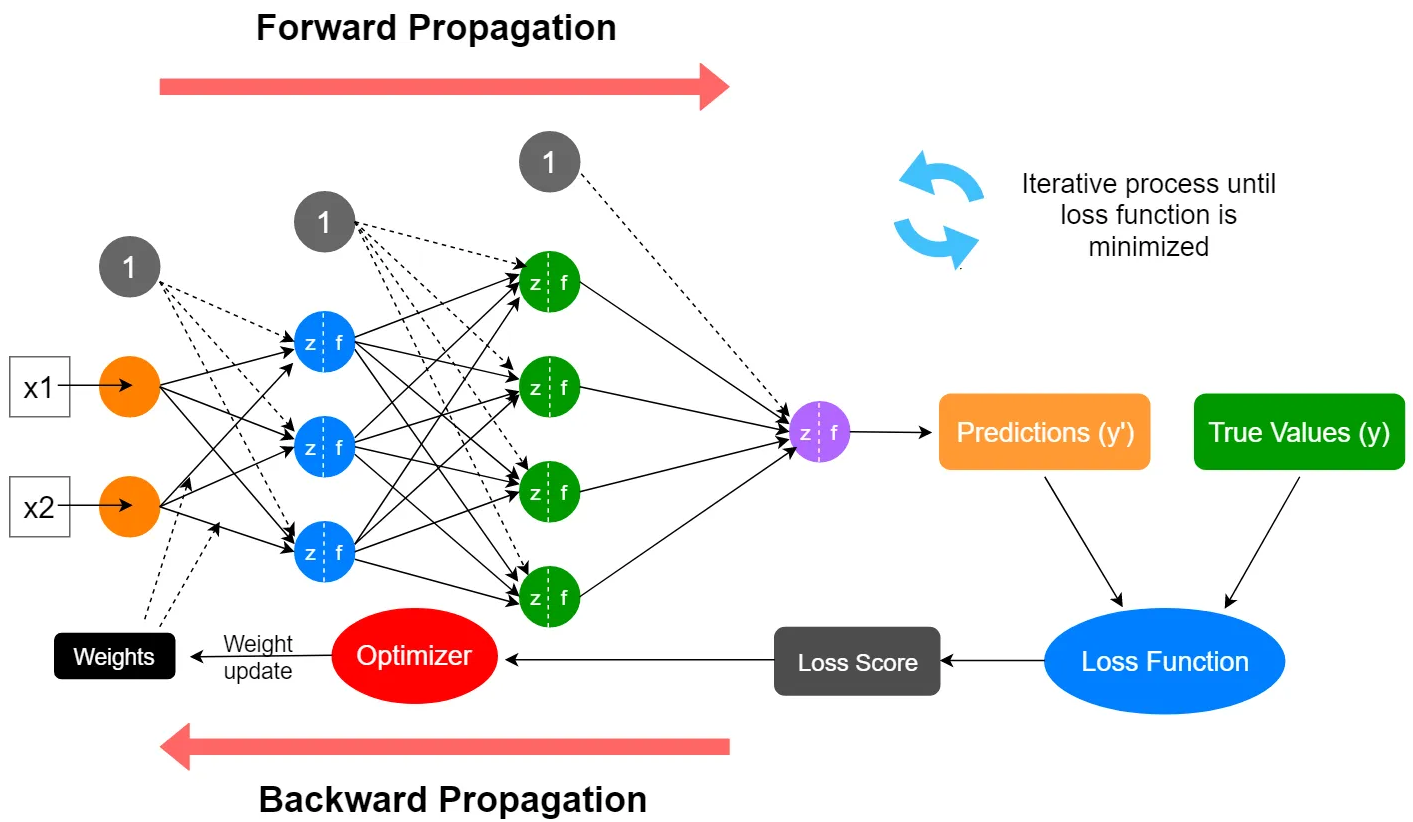obr. 1: Proces trénování hluboké neuronové sítě

Rozdělení hlubokých neuronových sítí

Hluboké neuronové sítě se mohou rozdělovat do několika kategorií na základě jejich architektury a propojení mezi vrstvami:

Vícevrstvý perceptron (MLP) - nejzákladnější forma hluboké neuronové sítě. Skládá se z jedné vstupní vrstvy, jedné nebo více skrytých vrstev a výstupní vrstvy. Váhy mezi neurony jsou přepojeny a každý neuron je propojen se všemi neurony v předchozí a následující vrstvě.
Konvoluční neuronové sítě (CNN) - často používány pro zpracování obrazových dat. Mají speciální konvoluční vrstvy, které efektivně extrahují rysy z obrázků pomocí konvolucí a sdílených vah. Konvoluční vrstvy jsou často střídány s vrstvami subvzorkování (pooling layers), které redukují rozměr dat.
Rekurentní neuronové sítě (RNN) - navrženy pro zpracování sekvencí dat, jako jsou časové řady nebo přirozený jazyk. Mají rekurentní vrstvy, které umožňují předávání stavů mezi časovými kroky, což umožňuje sítím uchovávat informace o historii vstupních dat.

Vrstvy

Hluboká neuronová síť může obsahovat různé vrstvy, v závislosti na konkrétní architektuře sítě a úkolu, který má řešit:

Konvoluční vrstvy - využívají konvoluce pro extrakci rysů z dat a sdílené váhy pro efektivní zpracování obrazových dat. Konvoluce je matematická operace, která se používá ke kombinaci dvou funkcí a v kontextu konvolučních vrstev umožňuje provádět lokální vážené součty mezi vstupními daty a váhami. Konvoluční vrstvy se skládají z několika filtrů, které jsou převedeny přes vstupní data. Každý filtr v konvoluční vrstvě obsahuje váhy, které reprezentují rysy, které se mají vyextrahovat z dat. Tyto váhy jsou optimalizovány během trénování sítě. Konvoluční vrstvy také často zahrnují aktivační funkci, jako je například ReLU (Rectified Linear Unit).
Pool vrstva (pooling layer), známá také jako subvzorkovací vrstva - používaná v konvolučních neuronových sítích pro snižování rozměru prostorových dat. Provádí subvzorkování, což je operace, která snižuje rozměr konvoluční mapy tím, že redukuje počet prvků na základě nějakého pravidla, například maxima nebo průměru. To pomáhá snížit počet parametrů v síti.


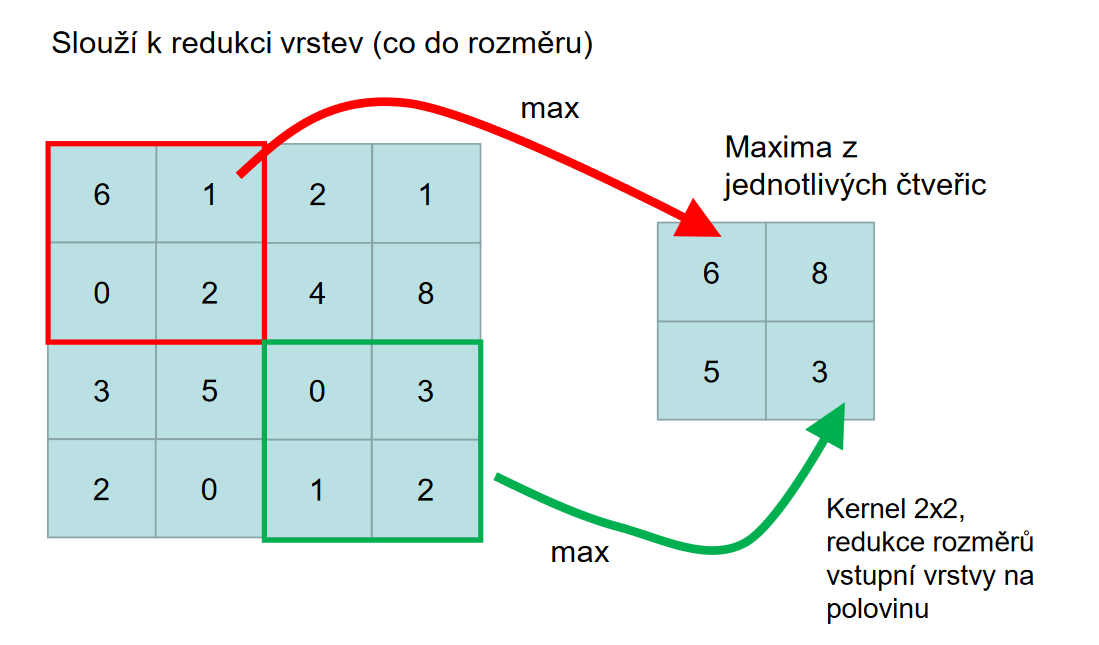obr. 2: Pool vrstva

Plně připojené vrstvy (fully connected layers), také nazývané jako "fc layers" - každý neuron je propojen s každým neuronem ve předchozí a následující vrstvě. V těchto vrstvách neexistuje žádná prostorová struktura jako u konvolučních vrstev. Typicky se používá na výstupu hluboké sítě a slouží k vykonání konečné klasifikace nebo regrese na základě naučených příznaků. Po průchodu plně připojenými vrstvami se obvykle používá softmax aktivační funkce.
Rekurentní vrstvy - mají zpětné propojení, které umožňuje předávání informací z předchozích časových kroků do budoucích.

Rozdělení vrstev u rozpoznávání obrázků je znázorněno na obrázku 3. ReLU vrstvu můžeme chápat jako skupinu neuronů, která používá ReLU aktivační funkce pro výpočet výstupů.


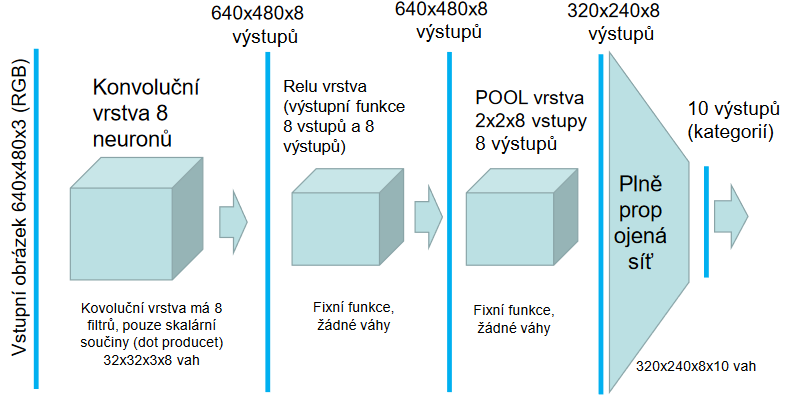obr. 3: Vrstvy CNN

Aktivační funkce

Aktivační funkce se používají v neuronových sítích k přidání nelinearity, normalizaci výstupů a vytvoření hladkých přechodů, což umožňuje síti aproximovat složité nelineární vztahy mezi vstupy a výstupy a dosáhnout plynulého učení a zpracování dat. Typické aktivační funkce jsou například:

ReLU (Rectified Linear Unit)- jedna z nejčastěji používaných aktivačních funkcí. Je definována jako max(0, x). To znamená, že pro nezáporné vstupy vrátí přímo hodnotu vstupu a pro negativní vstupy vrátí 0. ReLU přispívá k nelinearitě sítě a pomáhá snižovat problémy s postupným úmrtím neuronů.
Leaky ReLU - modifikace ReLU, která přidává malou nenulovou hodnotu pro negativní vstupy, například f(x) = max(ax, x) s a > 0. Tím se zabývá problémem nulového gradientu pro negativní vstupy v ReLU.
Parametrická ReLU (PReLU) - obdoba Leaky ReLU, ale místo pevně stanovené hodnoty má parametr, který je optimalizován během trénování.
Softmax - používá se pro klasifikaci mezi více třídami. Funkce se aplikuje na vnitřní potenciály všech neuronů vrstvy. Pro výstupy pak platí, že jsou v rozsahu (0,1) a součet všech výstupů je roven 1. Výstupy tak mohou být interpretovány jako pravděpodobnosti. Softmax je často používán jako poslední aktivační funkce v klasifikačních úlohách.
Sigmoidní funkce (sigmoid) - mapuje vstupní hodnoty na rozsah mezi 0 a 1, což je užitečné pro binární klasifikaci nebo jiné úlohy, které vyžadují pravděpodobnosti.
Hyperbolický tangent (tanh) - je podobný sigmoidní funkci, ale mapuje vstupní hodnoty na rozsah mezi -1 a 1.

Frameworky

Seznam nejznámějších frameworků pro učení hlubokých neuronových sítí:

TensorFlowm - jeden z nejpopulárnějších frameworků pro strojové učení a hluboké učení. Je vyvinutý společností Google a je známý pro svou efektivitu, flexibilitu a podporu pro distribuované výpočty.
PyTorch - open-source framework pro strojové učení, vyvinutý Facebookem. Má silnou podporu pro práci s grafickými procesory (GPU). PyTorch je nástupcem frameworku Theano.
Keras - vysoce abstraktní knihovna pro hluboké učení. Je nadstavbou nad frameworky jako TensorFlow nebo Theano a nabízí rychlý vývoj a experimentování s modely.
MXNet - framework pro hluboké učení s otevřeným zdrojovým kódem. Je navržený pro efektivní výpočetní grafy a podporuje různé programovací jazyky, včetně Pythonu, R, Julia a C++ a také podporuje distribuované učení.

Použití hlubokých neuronových sítí

Metodologie hlubokého učení se prosadila jako základní možnost pro řešení složitých problémů strojového učení jako je klasifikace obrazů, mluvené či psané řeči nebo překlady z jednoho přirozeného jazyka do jiného.

Zdroje

Přispěvatelé Wikipedie, Hluboké učení [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 7. 03. 2023, 15:08 UTC, [citováno 19. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Hlubok%C3%A9_u%C4%8Den%C3%AD&oldid=22524090
https://medium.com/data-science-365/overview-of-a-neural-networks-learning-process-61690a502fa

Konečný automat

Co je to konečný automat ?

Konečný automat je teoretický výpočetní model používaný v informatice pro studium formálních jazyků. Popisuje velice jednoduchý počítač, který může být v jednom z několika stavů, mezi kterými přechází na základě symbolů, které čte ze vstupu. Množina stavů je konečná (odtud název), konečný automat nemá žádnou další paměť, kromě informace o aktuálním stavu. Konečný automat je velice jednoduchý výpočetní model, dokáže rozpoznávat pouze regulární jazyky. Konečné automaty se používají při vyhodnocování regulárních výrazů, např. jako součást lexikálního analyzátoru v překladačích.

Konečný automat můžeme definovat jako uspořádanou pětici (Q, ∑, δ, q0, F) kde:

Q : Konečná neprázdná množina stavů
∑ : Konečná množina vstupních symbolů, take nazývaná abeceda. Neplést si se vstupním řetězcem.
q0 : počáteční stav
F : Množina koncových stavů (je podmnožinou Q)
δ : Přechodová funkce mezi stavy

Popis činnosti konečného automatu

Na počátku se automat nachází v definovaném počátečním stavu. Dále v každém kroku přečte jeden symbol ze vstupního řetězce a přejde do stavu, který je dán hodnotou, která v přechodové tabulce odpovídá aktuálnímu stavu a přečtenému symbolu. Poté pokračuje čtením dalšího symbolu ze vstupního řetězce, dalším přechodem podle přechodové tabulky atd.

Podle toho, zda automat skončí po přečtení vstupního řetězce ve stavu, který patří do množiny přijímajících stavů, platí, že automat buď daný vstupního řetězec přijal, nebo nepřijal. Množina všech řetězců, které daný automat přijme, tvoří regulární jazyk.

Pozn. Pokud má automat na vstupu symbol, ke kterému neexistuje přechodová funkce ze současného stavu, tak automat vstupní řetězec nepřijal. (Automat obsahuje tzv. dead state, do kterého kterého se automat přechodovou funkcí dostane, ale již se z něj nikdy nedostane) Toto nemusí platit u NFA, kde je možnost být ve více stavech najednou.

Reprezentace konečného automatu

Konečný automat lze reprezentovat několika způsoby. Bude následovat příklad vyjádření totožného konečného automatu třemi různými způsoby.

Výčtem prvků
Tabulkou
Přechodovým grafem
Regulárním výrazem (O tomto způsobu více v kapitole Konečné automaty a regulární jazyky)

Reprezentace výčtem prvků

A = (Q, ∑, δ, q0, F) - naše uspořádaná pětice
Q = (q0,q1,q2) - množina stavů, které automat obsahuje
∑ = (0,1) - symboly rozpoznávané konečným automatem
F = (q1)

δ(q0,0) = q1 (Toto je přechodová funkce která říká "Když jsi ve stavu q0 a na vstupu je symbol '0', tak jdi do stavu q1" )
δ(q0,1) = q2
δ(q1,0) = q1
δ(q1,1) = q0
δ(q2,0) = q2
δ(q2,1) = q2

Reprezentace tabulkou

A = (Q, ∑, δ, q0, F) - naše uspořádaná pětice
Q = (q0,q1,q2) - množina stavů, které automat obsahuje
∑ = (0,1) - symboly rozpoznávané konečným automatem
F = (q1)

Současný stav	0	1
->q0	q1	q2
q1	q1	q0
q2	q2	q2

(Všimněme si, že reprezentace se týká čistě přechodových funkcí)

Reprezentace grafem

A = (Q, ∑, δ, q0, F) - naše uspořádaná pětice
Q = (q0,q1,q2) - množina stavů, které automat obsahuje
∑ = (0,1) - symboly rozpoznávané konečným automatem
F = (q1)


obr. 1: Jednoduchý příklad (deterministického) konečného automatu

Deterministický konečný automat (DFA) vs Nedeterministický konečný automat (NFA)

Konečné automaty můžeme dělit na dva druhy.

Deterministický

Nepřijímá prázdný řetězec
Pro každý vstupní znak existuje nejvýše jeden stav, do kterého může automat přejít. Může se tedy v jednu chvíli nacházet právě v jednom stavu.
Z každého stavu by měli existovat přechodové funkce pro každý symbol z množiny ∑.
Přechodová funkce má tvar δ = Q x ∑ -> Q

Nedeterministický

Přijímá prázdný vstupní řetězec
Z jednoho stavu se lze dostat do více stavů zároveň. Automat se tedy může nechávat ve více stavech zároveň a pokud je po zpracování vstupního řetězce alespoň jeden z těchto stavů stavem konečným, je řetězec přijat.
Jednotlivé stavy nemusí mít přechodové funkce pro všechny symboly z množiny ∑.
Přechodová funkce má tvar δ = Q x ∑ -> 2^Q

Výše uvedené příklady reprezentace byly určeny pro DFA. Nyní vytvoříme podobné příklady pro NFA.

A = (Q, ∑, δ, q0, F) - naše uspořádaná pětice
Q = (q0,q1) - množina stavů, které automat obsahuje
∑ = (ε,0,1) - přidali jsme symbol 'ε', značící přechod bez nutnosti zpracování vstupního symbolu
F = (q1)

Současný stav	0	1
->q0	q1	nill
q1	q0	q0,q1

Grafická reprezentace by vypadala takto:


obr. 2: Nedeterministický konečný automat

Všimněme si "nedeterminističnosti" v podobě možnosti dostat se pomocí jedné přechodové funkce do dvou stavů zároveň.

Konverze NFA na jeho DFA ekvivalent

Platí, že každý DFA je ve skutečnosti NFA, ale ne naopak. DFA je podmnožinou NFA. Zároveň platí, že ke každému NFA lze sestrojit jeho DFA ekvivalent.

Proč ? Vychází to z definic přechodových funkcí
Pro DFA : δ = Q x ∑ -> Q
Pro NFA : δ = Q x ∑ -> 2^Q

Definice přechodové funkce pro NFA v sobě obsahuje definici přechodové funkce pro DFA. Ale ne naopak. NFA sice může přejít do více stavů zároveň za pomocí jednoho symbolu a může přejít do stavu bez zpracování symbolu, ale také nemusí. Na základě toho můžeme říct, že každý DFA je NFA, akorát tento NFA nemá žádné příznaky NFA.

Nyní pojďme převést náš NFA výše na DFA.

DFA nesmí mít více přechodů z jednoho stavu pro ten a samý symbol a měli by existovat přechodové funkce pro všechny symboly abecedy pro každý stav. Pokud by se v NFA nacházeli přechody Epsilon, tak se tyto dva stavy sloučí v jeden.

Postup je následovný (Nejlépe se dělá podle přechodové tabulky):

Přidáme tzv. dead state. Do tohoto stavu budeme svádět neexistující přechody již existujících stavů.
Pokud máme Epsilon přechody, zbavíme se jich tak, že přechod nahradíme přechody, které vedou ze stavu do kterého by jsme se skrze Epsilon přechod dostaly. Příklad zbavení se Epsilon přechodů můžeme najít v kapitole Konečné automaty a regulární jazyky.
Přidáme nový stav, pokud máme více přechodových funkcí z jednoho stavu pro ten a samý symbol, tedy přecházíme do dvou stavů zároveň. Tyto stavy spojíme do jednoho nového.
Aplikujeme operaci union na přechodové funkce stavů, které tento nový stav "pohltil", čímž získáme přechodové funkce pro náš nový stav.
Pokud jsou přechodové funkce nového stavu totožné s přechodovými funkcemi jednoho ze stavů, který byl použít k vytvoření nového, tak starý stav smažeme.

Úspěšně jsme naši DFA ekvivalent k našemu NFA z obrázku č. 2.

A = (Q, ∑, δ, q0, F) - naše uspořádaná pětice
Q = (q0,q1,q2) - množina stavů, které automat obsahuje
∑ = (0,1) - jedná se o DFA, nemá tedy možnost zpracovat prázdný řetězec F = (q1)

Současný stav	0	1
->q0	q1	q2
q01	q0	q01
q2	q2	q2


obr. 3: Deterministická verze konečného automatu z obrázku č. 2

Konečné automaty a regulární jazyky

Regulární jazyk je jediným druhem jazyka, který může být akceptován konečným automatem. Regulární jazyk je vyjádřen regulárním výrazem a tento regulární výraz může být vyjádřen v podobě konečného automatu a naopak, konečný automat může být vyjádřen regulárním výrazem. Pro každý regulární výraz R existuje konečný automat, který přijímá řetězce generované tímto regulárním výrazem.

Pro sestavení FA z regulárního výrazu postupujeme následovně:

Převedeme výraz na NFA s Epsilon přechody
Odstraníme Epsilon přechody
Převedeme NFA na DFA

Pro převod výrazu na NFA využijeme následující 'stavební bloky'


obr. 4: Základní konečné automaty pro regulární výrazy. Převzato z: https://www.tutorialspoint.com/how-to-convert-regular-expression-to-finite-automata

Řekněme, že máme regulární výraz, který generuje sekvenci písmen 'a' a 'b' nebo jedno jediné 'a'.
a + (a+b)*

Budeme tedy postupovat zleva doprava a krok po kroku vytvoříme náš NFA.


obr. 5: Inicializační krok


obr. 6: Rozdělení výrazu pomocí + operátoru


obr. 7: Přidání Epsilon přechodu, aby jsme mohli být v obou stavech najednou

Všimněme si, že krom epsilon operátoru jsme vycházeli čistě ze stavebních bloků popsaných na obrázku číslo 4 tak, že s každým rozdělením jsme přidali nový stav do kterého vede odpovídající přechodová funkce.

Nyní eliminujeme Epsilon přechod tak, že zduplikujeme přechody, které vedou ze stavu do kterého se skrze Epsilon dostaneme. Těmito přechody do patřičných stavů Epsilon nahradíme.


obr. 8: Nahrazení Epsilon přechodu

Nyní máme NFA, který odpovídá našemu regulárnímu výrazu. Na základě postupu z kapitoly Konverze NFA na jeho DFA ekvivalent nakonec vytvoříme ekvivalentní DFA.


obr. 9: DFA verze NFA

Pozn. Kdyby to bylo nutné, bylo by potřeba doplnit dead state tak, aby všechny stavy měly přechodové funkce ke všem prvkům vstupní abecedy.

Citace

GeeksForGeeks - *Introduction of Finite Automata [online] . @2022 [cit. 2023-04-22]. Dostupné z: https://www.geeksforgeeks.org/introduction-of-finite-automata/
Wikipedia: Open encyclopedia - *Finite-state machine [online]. @2023 [cit. 2023-04-22]. Dostupné z: https://en.wikipedia.org/wiki/Finite-state_machine
Michalův Web - KA02 – Způsoby zápisu konečných automatů [online] . @2023 [cit. 2023-04-22]. Dostupné z: http://michaluvweb.cz/2015/11/06/ka02-zpusoby-zapisu-konecnych-automatu/
Wikipedia: Open encyclopedia - Nondeterministic finite automaton [online]. @2023 [cit. 2023-04-22]. Dostupné z: https://en.wikipedia.org/wiki/Nondeterministic_finite_automaton
Javapoint - Conversion of RE to FA [online] . @2023 [cit. 2023-04-22].
Dostupné z: https://www.javatpoint.com/automata-conversion-of-re-to-fa
cstaalem - Elimination of Epsilon (ε) From NFA [online] . @2021 [cit. 2023-04-22].
Dostupné z: https://cstaleem.com/elimination-of-epsilon-%CE%B5-from-nfa

Regulární jazyky

Regulární jazyk je typ formálního jazyka v Chomského hierarchii. Je generovaný formální regulární gramatikou (gramatika konečněstavová) a rozpoznatelný tzv. konečným automatem.

Formální gramatika v informatice označuje strukturu, která popisuje formální jazyk.

Formální jazyk je libovolná množina konečných řetězců nad určitou abecedou.

Chomského hierarchie je hierarchie tříd formálních gramatik generujících formální jazyky. Skládá se ze 4 gramatik (poslední a nejjednodušší je právě ta, co generuje regulární jazyky).


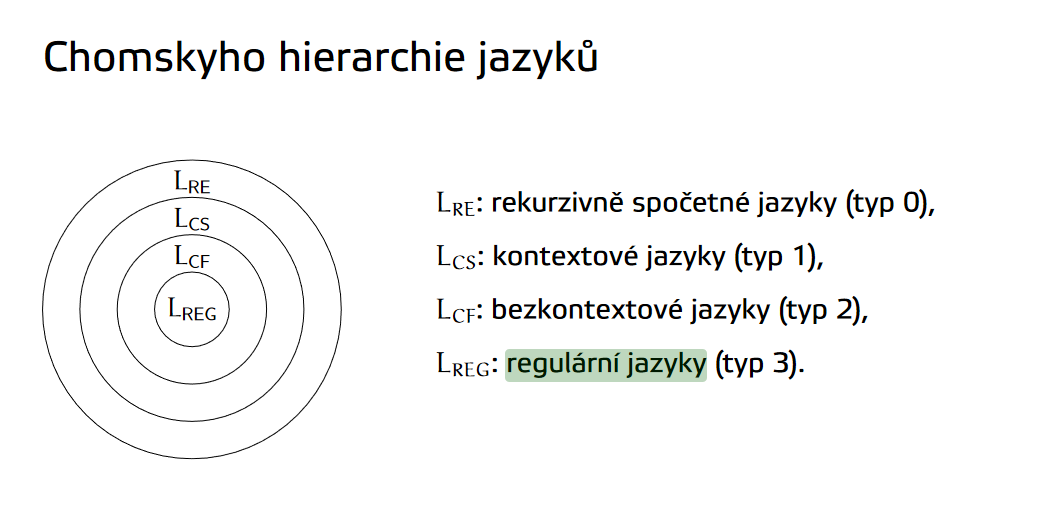obr. 1: Chomského hierarchie

Regulární výrazy

Pomocí symbolů abecedy Σ, závorek a operátorů + (sjednocení), · (zřetězení) a * (uzávěr) můžeme definovat složitější jazyky jako kombinace jednodušších.

Regulární výraz	Jazyk
a	{a}
a + b + c	{a, b, c}
(a + (b · c))*	{λ, a, bc, aa, abc, bca, bcbc, aaa, aabc, . . .}

Z toho vyplývá, že regulární výraz je posloupnost znaků a několika speciálních symbolů, jejichž vyhodnocením je (formální) jazyk.

Vlastnosti regulárních jazyků

Jazyk L(r) reprezentovaný regulárním výrazem r se nazývá regulární jazyk. Je definován následujícími pravidly:

regulární výraz Ø označuje prázdný jazyk
regulární výraz λ označuje jazyk {λ}
pro každé a ϵ Σ označuje regulární výraz a jednoprvkový jazyk {a}
pokud A a B jsou regulární jazyky, jsou A ∪ B (sjednocení), A ∙ B (konkatenace), a A* (iterace) také regulární.

Formální jazyk je regulární, právě když:

je akceptovaný nějakým deterministickým konečným automatem
je akceptovaný nějakým nedeterministickým konečným automatem
může být popsán regulárním výrazem
může být vygenerován regulární gramatikou

Všechny konečné jazyky jsou regulární a všechny regulární jazyky jsou bezkontextové.

Citace

Wikipedie: Otevřená encyklopedie: Chomského hierarchie [online]. c2022 [citováno 18. 01. 2023]. Dostupný z WWW: https://cs.wikipedia.org/w/index.php?title=Chomsk%C3%A9ho_hierarchie&oldid=21841492
PETKEVIČ, Vladimír. Regulární gramatika. CzechEncy - Nový encyklopedický slovník češtiny [online]. Brno, c2012-2020 [cit. 2023-01-18]. Dostupné z: https://www.czechency.org/slovnik/REGUL%C3%81RN%C3%8D%20GRAMATIKA

Bezkontextové gramatiky a jazyky

Bezkontextová gramatika je formální gramatika, ve které mají všechna přepisovací pravidla tvar
A → β
A je neterminál/proměnná a β je řetězec složený z terminálů nebo neterminálů/proměnných.

Gramatika je určena

Konečnou množinou neterminálních symbolů
Konečnou množinou terminálních symbolů, která nemá společné prvky s množinou neterminálů (Někdy také nazýváme tuto množinu abecedou jazyka, jež je generovaný touto gramatikou)
Počátečním neterminálem S
Konečnou množinou přepisovacích pravidel tvaru A → β, (A přepiš na β), kde A je neterminál a β je řetězec z neterminálů a terminálů

Bezkontextová gramatika je speciálním případem kontextové gramatiky, akorát kontext je prázdný.

Množina všech řetězců, jež jsou tuto gramatikou vygenerované se nazývá bezkontextový jazyk.

Co je to kontext ?

Kontextem se myslí symboly, které se nacházejí vedle neterminálů. U bezkontextové gramatiky platí, že nezávisle na tom, které symboly obklopují neterminál z levé strany, tak je možné tento neterminál nahradit některým přepisovacím pravidlem.

A → xBy
B → a | A

A => xAy => xxByy

Termíny/Pojmy

Přepsání : operace, při které se v řetězci složeném z terminálů a neterminálů nahradí podřetězec tvořící levou stranu nějakého pravidla gramatiky pravou stranou tohoto pravidla. Někdy se používá termín bezprostřední přepsání pro zdůraznění, že se jedná o jedno použití přepisovacího pravidla. Značí se =>.
Odvození : postup, při kterém se na řetězec uplatní konečný počet (žádné, jedno nebo více) přepsání.
Větná forma : libovolný řetězec složený z terminálů a neterminálů, který lze získat z počátečního symbolu konečným počtem přepsání.
Řetězec generovaný gramatikou : méně formálně věta gramatiky je větná forma, která je tvořena pouze terminálními symboly.
Jazyk generovaný gramatikou : množina všech řetězců, generovaných gramatikou.
Levá derivace neboli levé odvození : postup při generování určitého slova v bezkontextové gramatice, že se vždy přepisuje první neterminální symbol zleva. Bezkontextovost gramatiky umožňuje přepisovat neterminály v libovolném pořadí.
Pravá derivace neboli pravé odvození : postup při generování určitého slova v bezkontextové gramatice, že se vždy přepisuje poslední neterminální symbol (tj. první zprava).

Vlastnosti bezkontextových jazyků

Jak už jsme řekli, bezkontextový jazyk je generovaný bezkontextovou gramatikou. Na základě Chomského hierarchie se tedy jedná o jazyk generovaný gramatikou typu 2.

Jazyk je přijímaný zásobníkovým automatem (nikoliv konečným automatem, ten je schopen přijímat pouze jazyky generované regulérní gramatikou).
Jazyk je uzavřený vůči zřetězení, sjednocení, iteraci, substituci a morfismu s regulárním jazykem. To znamená, že výsledkem těchto operací stále bude bezkontextový jazyk
Jazyk není uzavřená vůči průniku a rozdílu s regulárním jazykem. Výsledkem těchto operací již nebude bezkontextový jazyk.
Každý regulární jazyk je také bezkontextový, ale obráceně to neplatí.
Když se během posloupnosti přepisů někde objeví terminální symbol, už tam zůstane.
Přepisy různých proměnných jsou navzájem nezávislé:
Mámeli řetěz xAyBz, můžeme postupně přepisovat proměnné A a B v libovolném pořadí.

Příklady zápisu

Gramatika je zadána nějakým přepisovacím pravidlem. V našem případě jsme dostaly následující přepisovací pravidlo :

S → aSb | ab

Vidíme, že toto přepisovací pravidlo odpovídá tvaru přepisovacího pravidla pro bezkontextovou gramatikou:

A → β (A je neterminál a β je řetězec složený z terminálů/neterminálů)

Pokud bychom chtěli získat řetězec, jež je generovaný touto gramatikou, použijeme k tomu odvození.

Rozepíšeme se naše pravidlo a postupně nahrazujeme neterminály, dokud nedostaneme požadovaný řetězec, nebo dokud nám nedojdou neterminální symboly na pravé straně.

S → aSb
S → ab
→ aaSbb
→ aaaSbbb
→ aaaabbbb

Příklady řetězců generovaných touto bezkontextovou gramatikou: ab, aabb, aaabbb, ...

Zápis může být také proveden tzv. derivačním stromem.

Zápis pomocí derivačního stromu

Mějme bezkontextovou gramatikou danou přepisovacími pravidly ve tvaru:

(1) S → S + S
(2) S → 1
(3) S → a

Použijme nyní postup levého odvození pro získání řetězce 1 + 1 + a.

S → S + S (1)
=> S + S + S (1)
=>1 + S + S (2)
=> 1 + 1 + S (2)
=> 1 + 1 + a (3)

Všimněme si, jak levé odvození funguje. Nahrazuje vždy první neterminální symbol na pravé straně. Pravé odvození by nahrazovalo vždy poslední neterminální symbol na pravé straně.

Tento postup může být znázorněn také jako strom:

       S
      /|\
     / | \
    /  |  \
   S  '+'  S
  /|\      |
 / | \     |
S '+' S    a
|     |
1     1

Tomuto se říká konkrétní syntaktický strom řetězce

K výsledku (1 + 1 + a) můžeme dojít i jiným způsobem

S → S + S (1)
=> 1 + S (2)
=> 1 + S + S (1)
=> 1 + 1 + S (2)
=> 1 + 1 + a (3)

       S 
      /|\
     / | \
    /  |  \
   S  '+'  S
   |      /|\
   |     / | \
  '1'   S '+' S
        |     |
       '1'   'a'

Pokud pro určitý řetězec v jazyce gramatiky existuje více než jeden parsovací strom, potom se tato gramatika nazývá nejednoznačná gramatika.

Některé gramatiky se dají těžko rozebírat, protože syntaktický analyzátor (parser) neví, které z přepisovacích pravidel má použít. Obvykle mnohoznačnost je charakteristická pro gramatiku, což neplatí pro jazyk.

Normální formy

Používají se ke zjednodušení bezkontextových gramatik. Ke každé bezkontextové gramatice lze sestrojit gramatiku v Chomského normální formě a v Greibachové normální formě, které jsou s původní gramatikou ekvivalentní. Ekvivalentní gramatiky jsou takové, které generují stejný jazyk.

Chomského normální forma:
- všechna odvozovací pravidla tvaru:
- A → BC nebo
- A → a nebo
- S → ε (je povoleno pokud gramatika generuje prázdný řetězec a zároveň se S nevyskytuje na pravé straně žádného pravidla)
- kde A, B a C jsou neterminály, 'a' je terminál, S je startovní neterminál a ε je prázdný řetězec, přičemž B ani C nemohou být startovacím neterminálem.
- Každá gramatika v Chomského normální formě je bezkontextová a naopak, každou bezkontextovou gramatiku lze transformovat do Chomského normální formy.
- S výjimkou volitelného pravidla S → ɛ jsou všechna pravidla nezkracující, tzn. při každém odvození je každý řetězec stejně dlouhý nebo delší než předchozí (ve významu času) řetězec. Jelikož všechna pravidla odvozující neterminály transformují jeden neterminál na právě dva, je parsovacím stromem binární strom a jeho výška je maximálně délka generovaného řetězce.
Greibachové normální forma:
- všechna odvozující pravidla mají tvar:
- A → aX nebo
- S → ε
- Přičemž A je neterminál, 'a' je terminál, S je startovní neterminál, X je (případně prázdná) posloupnost neterminálních symbolů (ve které se nevyskytuje S, pokud gramatika obsahuje pravidlo S → ε) a ɛ je prázdný řetězec.
- Gramatika v Greibachové normální formě postrádá levou rekurzi. Každá bezkontextová gramatika může být transformována do Greibachové normální formy. Gramatika v Greibachové normální formě je díky absenci levé rekurze ideální k sestrojení predikativního parseru za pomocí LL gramatiky.

Proč ale chceme upravovat přepisovací pravidla, aby vyhovovali jedné ze dvou norem? Důvodem je sestrojení něčeho, co dokáže v konečném čase říci, zdali daný řetěz patří do jazyka, či nikoliv.

Motivace: Chceme vědět, jestli řetězec patří do jazyka, jež je popsaný určitými přepisovacími pravidly.

Zásobníkový automat


obr. 1: Zásobníkový automat (PDA) Dostupné z: https://elearning.jcu.cz/pluginfile.php/279723/mod_resource/content/9/prezentace.pdf

Nedeterministický zásobníkový automat je uspořádaná sedmice
M = (Q, Σ, Γ, δ, q0, z, F)

Q je konečná množina stavů řídící jednotky;
Σ je konečná vstupní abeceda;
Γ je konečná množina symbolů – abeceda zásobníku;
δ je přechodová funkce – funkce z Q × (Σ ∪ {λ}) × Γ do množiny všech konečných podmnožin kartézského součinu Q × Γ
- Příklad: δ(q0, a, 1) = {(q1, 11)} toto čteme jako : Jsme ve stavu q0, pokud je na vstupu 'symbol a' a v zásobníku 'symbol 1', jdi do stavu q1 a do zásobníku přidej symboly '11'.
q0 ∈ Q je počáteční stav řídící jednotky;
z ∈ Γ je počáteční symbol zásobníku ;
F ⊆ Q je množina koncových stavů řídící jednotky.

Automat lze vyjádřit:

Přechodovou tabulkou
grafem přechodů
Obojí získáme z přepisovacích pravidel bezkontextové gramatiky, které jsou pokud možno v jedné ze dvou normálních forem

Rozlišujeme dva druhy zásobníkových automatů

deterministické (DPA)
- Je pouze jedna možnost jak přejít ze stavu do stavu pomocí jednoho symbolu
- Každý DPA lze převést na NDPA
- Jazyk přijímaný DPA je podmnožinou jazyka přijímaného NDPA
- Přijímá pouze deterministické bezkontextové jazyky
nedeterministické (NDPA)
- Je více možností jak přejít ze stavu do stavu pomocí jednoho symbolu
- Ne každý NDPA lze převést na DPA
- Přijímá jak deterministické bezkontextové jazyky, tak nedeterministické

Zásobníkové automaty mohou používat lambda přechody a být stále deterministické, protože se řídí nejen symbolem na vstupu, ale i symbolem/y nacházejícím se na zásobníku. Oproti konečným automatům, které ví jen to co je (stav) a to co bude (symbol -> další stav), tak zásobníkové automaty ví i to co bylo (symboly v zásobníku). Mohou tedy rekurzivně určit následující stav na základě aktuálního stavu, vstupního znaku a předchozí sekvence znaků, jež se nachází v zásobníku. Mají paměť. Jedná se o nejjednodušší případ syntaktického analyzátoru metodou shora dolů.

Pro jednodušší konstrukci zásobníkového automatu potřebujeme, aby byla gramatika pokud možno v Greibachové normální formě (GNF).

Na základě přepisovacích pravidel lze sestrojit zásobníkový automat následovně:

vložíme S do zásobníku
simulujeme přepisovací pravidla aplikovaná vždy na nejlevější proměnnou v odvozovaném slově (= levé odvození).
- příklad :
  Mámeli na vrcholu zásobníku proměnnou A a na vstupu znak a, vybereme nějaké pravidlo tvaru
  A → ax a proměnnou A v zásobníku nahradíme řetězem proměnných x.


obr. 2: Získání přechodové tabulky z přepisovacích pravidel Dostupné z: https://elearning.jcu.cz/pluginfile.php/279723/mod_resource/content/9/prezentace.pdf

Určení, zdali je jazyk generovaný gramatikou bezkontextový

Pokud máme nějaký jazyk L, může nás zajímat, o jaký druh jazyka jde. Je jazyk bezkontextový? K tomuto účelu slouží pumpovací lemma.

Pumpovací lemma

Pumpovací lemma si zakládá na tvrzení, že pro jakýkoliv bezkontextový jazyk L je možné najít v dostatečně dlouhém řetězci generovaném jazykem dva podřetězce, které je možné n krát opakovat tak, aby výsledný řetězec stále patřil do tohoto jazyka.

Pumpovací lemma nám není schopné říct, zdali jazyk generovaný gramatikou je bezkontextový. Může nám pouze říct, že není.

Podobný princip funguje i pro regulární jazyky.

Zdroje

Wikipedie: Otevřená encyklopedie - Bezkontextová gramatika [online]. @2023 [cit. 2023-04-23]. Dostupné z: https://cs.wikipedia.org/wiki/Bezkontextov%C3%A1_gramatika
Wikipedie: Otevřená encyklopedie - Terminální a neterminální symbol [online]. @2023 [cit. 2023-04-23]. Dostupné z: https://cs.wikipedia.org/wiki/Termin%C3%A1ln%C3%AD_a_netermin%C3%A1ln%C3%AD_symbol
Wikipedia: Open encyclopedia - Pumping lemma for context-free languages [online]. @2023 [cit. 2023-04-23]. Dostupné z: https://en.wikipedia.org/wiki/Pumping_lemma_for_context-free_languages
Wikipedie: Otevřená encyklopedie - Bezkontextový jazyk [online]. @2023 [cit. 2023-04-23]. Dostupné z: https://cs.wikipedia.org/wiki/Bezkontextov%C3%BD_jazyk
GeeksForGeeks - Various Properties of context free languages [online]. @2023 [cit. 2023-04-23]. Dostupné z: https://www.geeksforgeeks.org/various-properties-of-context-free-languages-cfl/
Lhotka Ladislav - Teoretická informatika [online]. @2021 [cit. 2023-04-23]. Dostupné z: https://elearning.jcu.cz/pluginfile.php/279723/mod_resource/content/9/prezentace.pdf

Syntaktická analýza a LL gramatiky

Tento okruh vychází ze znalosti okruhu Bezkontextové gramatiky a jazyky.

Syntaktická analýza, neboli parsing má největší uplatnění při návrhu programovacích jazyků. Rozlišujeme syntaktická a sémantická pravidla.

Syntaktická pravidla se vyjadřují pomocí přepisovacích pravidel bezkontextové gramatiky.

Pro syntaktickou analýzu je třeba kromě určení, zda w ∈ L(G) (je řetězec w slovo generované jazykem L, jež popisuje gramatika G?), také najít odvození S ⇒ w, tj. určit, z jakých syntaktických celků se w skládá (klíčové slovo, operátor, číslo, ...).

Syntaktický analyzátor bere jako vstup řetězec tokenů, které jsou získány skrze lexikální analýzu a porovná tento řetězec s přepisovacími pravidly. Výstupem je parsovací strom.


obr. 1: Postup syntaktické analýzy
dostupné z: https://elearning.jcu.cz/pluginfile.php/279723/mod_resource/content/9/prezentace.pdf

Tento okruh se zaobírá syntaktickou analýzou shora dolů, tedy od kořene stromu, až k jeho listům, kde se nacházejí terminály. Syntaktická analýza zdola nahoru naopak funguje na principu toho, že začínáme u terminálů a výsledkem je startovní symbol (kořen).

Syntaktickou analýzu shora dolů lze provést následujícími způsoby:
- Analýza rekurzivním sestupem (Analýza hrubou silou, obsahuje backtracking)
- Analýza ne-rekurzivním sestupem (bez backtrackingu, LL(1) parser nebo také predikativní parser)


obr. 2: Rozdělení syntaktických analyzátorů
dostupné z: https://elearning.jcu.cz/pluginfile.php/279723/mod_resource/content/9/prezentace.pdf

Základním způsobem, jež samozřejmě má své nevýhody, je provést analýzu hrubou silou - analýzu všech možností.

Pro připomenutí:

Gramatika G je popsána uspořádanou čtveřicí (V, T, S, P)
- V: množina všech neterminálních symbolů (proměnných)
- T: množina všech terminálních symbolů (abeceda)
- S: počáteční symbol jež patří do množiny V
- P: konečný set přepisovacích pravidel

Analýza všech možností

vezmeme všechna pravidla tvaru S → x1, kde x1 ∈ (V ∪ T) a x1 může být řetězec složený z terminálů a neterminálů
pro všechna taková x1 vezmeme všechna pravidla tvaru A1 → x2, kde A1 je první proměnná (neterminál) v x1 (nejvíc vlevo)
pokud se některou cestou dostaneme až ke slovu w, máme hledané (levé) odvození
- dospějemeli k řetězu, z něhož určitě nelze w odvodit, větev ukončíme
- tento přístup se též nazývá analýza hrubou silou
- jde o typ analýzy shora dolů

Nevýhody

hledání nemusí skončit
- pokud řetězec w nepatří do jazyka L generovaného gramatikou G, můžeme vytvářet stále delší cesty a nikdy nedospět k cíli -> nemůžeme předem s jistotou určit, jestli w do jazyka patří, či nikoliv
- příklad:
  - hledáme odvození slova aabb
  - gramatika je popsaná přepisovacím pravidlem: S → SS | aSb | bSa | λ
  - tento problém odstraníme tak, že gramatiku upravíme aby neobsahovala žádná vypouštěcí (S -> λ), či jednotková (A -> B) pravidla
  - po úpravě dostaneme: S → SS | aSb | bSa | ab | ba
  - algoritmus je poté schopen pro každý řetězec w rozhodnout, zdali patří do jazyka, či nikoliv
  - počet k tomu nutných odvození je poté maximálně dvojnásobek délky hledaného slova, tedy maximálně 2|w|
exponenciální složitost
- v každém kroku algoritmu můžeme v nejhorším případě použít všechna přepisovací pravidla
- s rostoucí velikostí w tedy roste složitost algoritmu až exponenciálně
- důvodem je, že u analýzy hrubou silou předem nevíme, jaké přepisovací pravidlo vybrat
- složitost tohoto algoritmu může dosahovat až O(n!)

Shrnutí: Přepisovací pravidla, jež popisují bezkontextový jazyk generovaný bezkontextovou gramatikou umožňují odvození řetězce hrubou silou. Tento přístup je však velice neefektivní a časově náročný, kde algoritmus sází na vysokou výpočetní sílou procesoru. Pro zlepšení algoritmické složitosti (pokud možno získání lineární složitosti) můžeme použít jiný druh parsování, jako je například zde rozebíraný predikativní parser.

Pro další postup je potřeba gramatiku upravit do tzv. normálních forem (pokud jsme to již neudělali pro její zjednodušení dříve).

Chomskyho normální forma (CNF)
Greibachové normální forma (GNF)

Motivace: Nechť L je bezkontextový jazyk neobsahující λ. Potom existuje bezkontextová gramatika, která generuje L a přitom neobsahuje žádné zbytečné proměnné a produkce, λ-produkce ani jednotkové produkce. Pokud máme bezkontextový jazyk, který neobsahuje λ, pak je možné ho upravit do jedné z normálních forem.

Úprava přepisovacích pravidel

odstranění λ produkcí
odstranění jednotkových produkcí
odstranění zbytečných produkcí a proměnných
- produkce jsou zbytečné, pokud jsou stejné jako jiné produkce
- proměnná je zbytečná, pokud stejného výsledků dosáhneme odvozením skrze jinou proměnnou

Proč ale chceme upravovat přepisovací pravidla, aby vyhovovali jedné ze dvou norem a navíc jsme odstranili λ produkcí?. V kontextu syntaktické analýzy chceme tuto gramatiku převést na LL gramatiku, abychom pomocí ní mohli sestrojit predikativní parser.

LL gramatiky

Jedná se o bezkontextové gramatiky, které neobsahují levou rekurzi a jsou jednoznačné.

Levá rekurze:

S -> aAb
A -> Aa - tady se nachází levá rekurze, toto není LL gramatika
A -> λ

Jednoznačná gramatika:

Taková gramatika, kdy pro každé slovo w generované jazykem popsaným touto gramatikou existuje pouze jeden derivační strom, tedy pouze jedna sada odvození skrze přepisovací pravidla.

Využití LL gramatik:

Následující přepisovací pravidlo můžeme přesně určit, pokud se podíváme na omezenou část vstupního řetězu (příští symbol + pevný počet dalších). První L: vstup čteme odleva, druhé L: děláme levé odvození. LL(k): díváme se na k vstupních symbolů, speciálně u LL(1) jen na následující.

Toto vede k sestrojení predikativního parseru.

Predikativní parser

Řada programovacích jazyků je definována pomocí LL gramatik a jejich kompilátory využívají LL analyzátory. Pro LL(k) gramatiku lze vytvořit prediktivní parser, který je v každém kroku analýzy schopen vybrat správnou produkci (přepisovací pravidlo) na základě prvních k terminálů v dosud nezpracované části vstupního řetězu.

Parser tohoto docílí na základě parsovací tabulky. Ta mu říká, jaké pravidlo má vybrat na základě k vstupních symbolů.

Analýza tímto způsobem spadá do kategorie parsování rekurzivním sestupem. Predikativnímu parseru jež využívá LL(1) gramatiku se také říká LL(1) parser.


obr. 3: Příklad parsovací tabulky, kde k = 1
dostupné z: https://elearning.jcu.cz/pluginfile.php/279723/mod_resource/content/9/prezentace.pdf

Sestavení predikativního parseru se staví na dvou funkcích:

FIRST
FOLLOW

Funkce FIRST

Funkce FIRST(x) jednoznačně určuje, který další znak následuje při odvození x.

L -> aB
L -> c
L -> λ
funkce FIRST(L) = FIRST {a,c,λ}

Funkce FOLLOW

Funkce FOLLOW(x) říká, jaký symbol následuje za neterminálem x, který odvozujeme. Do funkce FOLLOW automaticky spadá prázdný řetězec.

L -> aBa
funkce FOLLOW(B) = FOLLOW {$,a}

Na základě těchto funkcí poté můžeme sestavit parsovací tabulku, která nám umožní určit, jakou produkci (přepisovací pravidlo) vybrat.


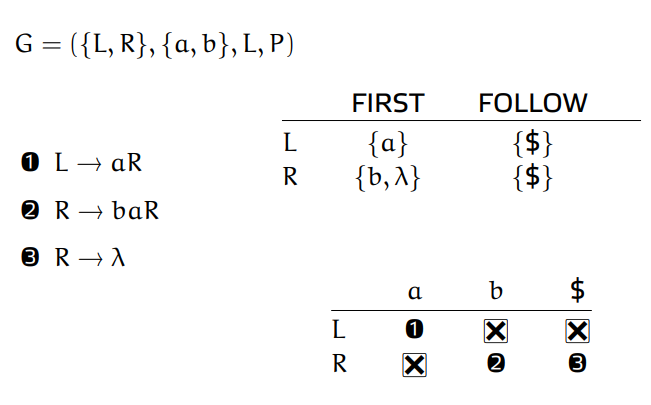obr. 4: Sestavení parsovací tabulky
dostupné z: https://elearning.jcu.cz/pluginfile.php/279723/mod_resource/content/9/prezentace.pdf

Zdroje

Wikipedie: Otevřená encyklopedie - Syntaktická analýza [online]. @2023 [cit. 2023-04-23].
Dostupné z: https://cs.wikipedia.org/wiki/Syntaktick%C3%A1_anal%C3%BDza
Wikipedie: Otevřená encyklopedie - LL syntaktický analyzátor [online]. @2023 [cit. 2023-04-23].
Dostupné z: https://cs.wikipedia.org/wiki/LL_syntaktick%C3%BD_analyz%C3%A1tor
Lhotka Ladislav - Teoretická informatika [online]. @2021 [cit. 2023-04-23].
Dostupné z: https://elearning.jcu.cz/pluginfile.php/279723/mod_resource/content/9/prezentace.pdf
GeeksForGeeks - Types of Parsers in Compiler Design [online]. @2021 [cit. 2023-04-25].
Dostupné z: https://www.geeksforgeeks.org/types-of-parsers-in-compiler-design/
GeeksForGeeks - Construction of LL(1) Parsing Table [online]. @2021 [cit. 2023-04-25].
Dostupné z: https://www.geeksforgeeks.org/construction-of-ll1-parsing-table/
Buchiredddypalli Koushik - What is left recursion and how do you eliminate left recursion? [online]. @2021 [cit. 2023-04-25].
Dostupné z: https://www.educative.io/answers/what-is-left-recursion-and-how-do-you-eliminate-left-recursion

Turingův stroj

struktura a výpočty

Turingův stroj je teoretický model počítače navržený britským kryptoanalytikem a matematikem Alanem Turingem (za II. světové války byl jedním z předních kryptoanalytiků, kteří dešifrovali zprávy šifrované prostřednictvím Enigmy). Turingův stroj slouží k modelování algoritmů v teorii vyčíslitelnosti (věda zkoumající algoritmickou řešitelnost problémů).

Turing například dokázal, že neexistuje takový obecný algoritmus, který by řešil problém zastavení programu pro všechny vstupy všech programů.

Konečnost programu

I když znám zdrojový kód programu a vstup, tak nejsem vždy schopný říci, zda program poběží do nekonečna nebo se zastaví.

Definice Turingova stroje

Turingův stroj se skládá z:

řídící jednotky s konečným počtem stavů
konečné množiny pravidel definujících přechodovou funkci
pravostranně nekonečné pásky pro vstup a zápis mezivýsledků

Turingova teze & Turingovská úplnost

Turingova teze: ke každému algoritmu existuje ekvivalentní Turingův stroj
Turingovská úplnost: turingovsky úplné jsou právě ty programovací jazyky nebo počítače, které mají stejnou výpočetní sílu jako Turingův stroj (jsou schopny spočítat vše, co Turingův stroj, tedy každý algoritmus (viz Turingova teze))

TS je sedmice: $M = (Q, \varGamma, b, \Sigma, q_0, \delta, F)$

$Q$ je konečná množina stavů
$\varGamma$ je konečná abeceda symbolů na pásce
$b$ je prázdný symbol (náleží do $\varGamma$)
$\Sigma$ je konečná množina vstupních symbolů (je podmnožinou $\varGamma$, $b$ není součástí)
$q_0$ je počáteční stav
$\delta$ je přechodová funkce: $(Q / F) \times \varGamma \Rightarrow Q \times \varGamma \times (L, R) $
- $L$ - posun hlavy vlevo
- $R$ - posun hlavy vpravo
$F$ je množina koncových stavů (podmnožina $Q$)

Konfigurace TS

aktuální stav q
počáteční úsek pásky s obsahující neprázdné symboly
pozice hlavy (tvořené číslem/indexem buňky n)

Formálně se jedná o uspořádanou trojici $(q, s, n)$. Kde $q \in Q, s \in \varGamma, n \in N_0$

Počáteční konfigurace pro vstup w je $(q_0, w, 0)$.

Výpočet

Na počátku je TS v počáteční konfiguraci a na pásce je zapsané vstupní slovo. Poté pracuje následovně:

je-li aktuální stav koncovým stavem, výpočet je úspěšný
hlava přečte vstupní symbol z buňky, kde se právě nachází
není-li pro aktuální stav a přečtený symbol definována hodnota přechodové funkce, výpočet je neúspěšný
jinak se provede instrukce popsaná hodnotou přechodové funkce (u nedeterministických strojů se vybere jeden přechod náhodně)
- změní se stav
- na aktuální pozici hlavy se zapíše příslušný symbol
- hlava se posune o jednu pozici doleva nebo doprava

Příklady

Videa na pěkné příklady zde a zde.

Zdroje

Algoritmická řešitelnost

Číselné soustavy

Převody číselných soustav, základní operace ve dvojkové soustavě. Kódování znaků v počítači, reprezentace čísel se znaménkem a čísla v plovoucí řádové čárce.

Rozlišení soustav a historický zápis čísel

Číselná soustava nám charakterizuje způsob reprezentace čísla. Rozlišujeme dva hlavní druhy číselných soustav, dle způsobu určení jeho hodnoty:

Nepoziční
Poziční

Nepoziční

Hodnota číslice není dána polohou v dané sekvenci číslic. Neobsahují v mnoha případech hodnotu pro 0 a záporná čísla. Zápis komplexnějších čísel je poměrně dlouhý.

zářezy na holi (zářezy, které po určitém počtu přeškrtneme), jak počítání týdnů ve věznici :-)
římské číslice
egyptské číslice
řecké číslice (alfabeta)

Římské číslice, I až III dle prstů na rukou. Dále dle rčení: Ivan Vedl Xénii Lesní Cestou Do Města.

Tedy: I, V, X, L, C, D, M $\iff$ 1, 5, 10, 50, 100, 500, 1000

Poziční

Charakteristické základem neboli bází (eng. radix). Radixem je kladné celé číslo definující maximální počet číslic, které jsou v dané soustavě k dispozici.

V přednáškách jsme používali místo r, písmeno Z, jako Základ.

Poziční soustavy se kromě jedničkové nazývají také polyadické - číslo v nich napsané, lze vyjádřit součtem mocnin základu dané soustavy vynásobeným příslušnými platnými číslicemi.

Nejčastější poziční soustavy

jedničková, r = 1 (počítání na prstech)
dvojková (binární) r = 2
osmičková (oktální/oktalová), r = 8
dekadická, r = 10
dvanáctková, r = 12 (již se nepoužívá, ale známe tucet a veletucet)
šestnáctková (hexadecimální), r= 16, pro čísla 10-15 se používají písmena A-F
šedesátková, r = 60 (měření času pro zlomky hodiny)

Každé číslo v poziční soustavě (kromě jedničkové) může mít celočíselnou část a zlomkovou část, oddělují se čárkou (anglosaské země oddělují tečkou).

Z-ADICKÁ SOUSTAVA: $A_z = (a_n a_{n-1} ...a_1 a_0 , a{-1} a{-2} + ...a_{-m})_z; a_i, n, m \in N$

$a_i$ je z-adická číslice
z je báze soustavy
n je nejvyšší řád s nenulovou číslicí
m je nejnižší řád s nenulovou číslicí

Binární soustava

Zde se Z (báze) = 2.


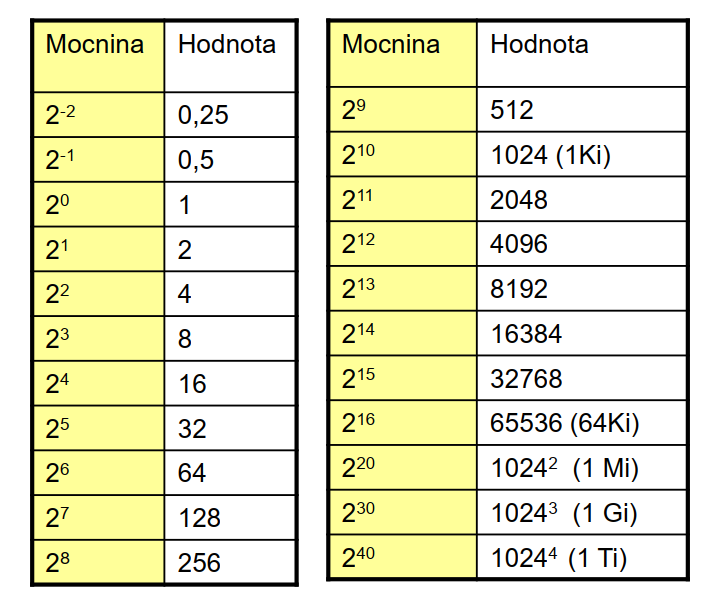obr. 1: Binární soustava
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.

Ki (kibi)
Mi (mebi)
Gi (gibi)

Převody do jiné soustavy

Ukážeme si převod do dekadické soustavy. Máme dvě možnosti:

A) buď si převáděné číslo rozepíšeme na polynom a vyčíslíme v dané soustavě

$A = 1001101_2$ $A = 1 * 2^6 + 0 * 2^5 + 0 * 2^4 + 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77$

B) použijeme tzv. modulo (%) - algoritmus zbytku po dělení


obr. 2: Převod z BIN soustavy do DEC soustavy
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.

Výsledný sloupec do binární soustavy zapisujeme odspoda nahoru.

Převod zlomkové části na intervalu <0, 1)

mějme číslo v desítkové soustavě 0,375
převádíme následovně:

$0,375 * 2 = 0,75$
$0,75 * 2 = 1,5$
$0,5 * 2 = 1$

Tedy, nalevo před desetinnou čárkou bude zákonitě 0. Poté napravo zapisujeme čísla z výsledků, která jsou PŘED danými desetinnými čárkami.

$0,375_{10} = 0,011_2$

Převod z Binární do Decimální soustavy

Buď provedeme binární dělení, tedy číslo zaspané v binární soustavě budeme dělit $10$ zapsanými také v bináru, nebo si jednoduše rozepíšeme řadu v mocninách čísla 2 a sečteme.

Totéž uděláme pro zlomkové části (tedy za desetinnou čárkou). Zde je třeba si pamatovat, že první číslo za desetinnou čárkou/tečkou je $2^{-1}$, protože poslední číslice z celého čísla je $2^0$.

Příklady

$1 0 1 1 0 1$ $\Rightarrow$ $1 * 2^5 + 0 * 2^4 + 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 32 + 8 + 4 + 1 = 45$

$1 1 0 0.1 0 1$ $\Rightarrow$ $2^3 + 2^2 . \frac{1}{2} + \frac{1}{8}$ $\Rightarrow$ $12.625$

Sčítání, násobení a dělení čísel v binární soustavě


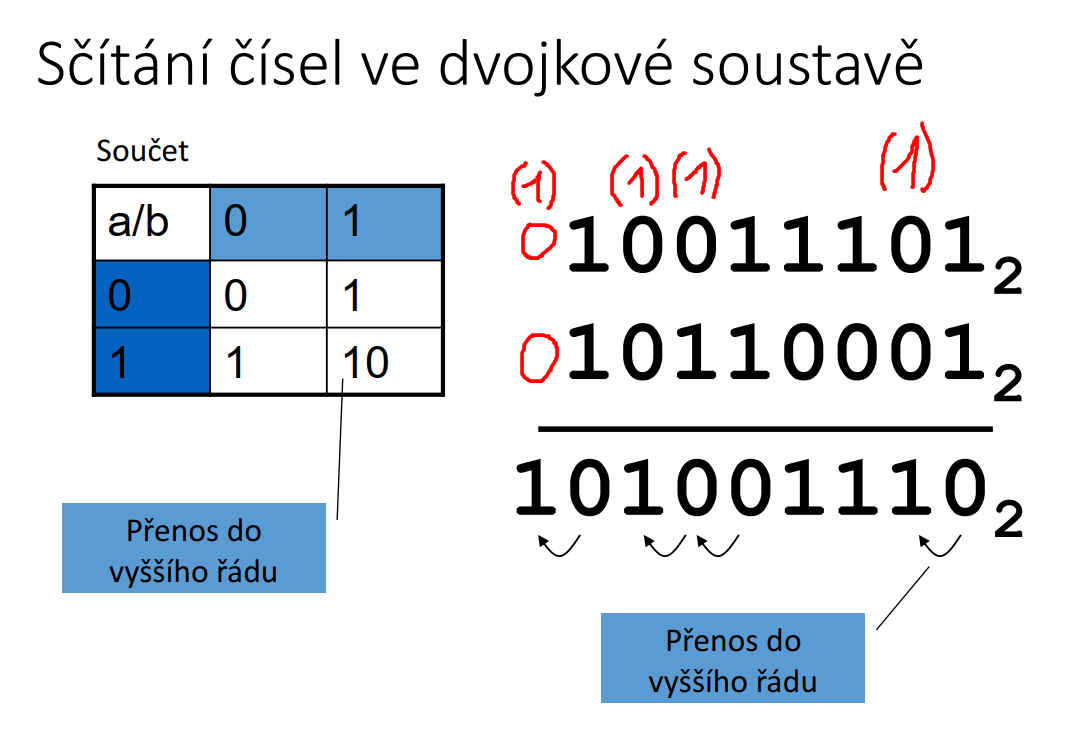obr. 3: Sčítání v binární soustavě
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.

Sčítáme obdobně jako v dekadické soustavě, jen s tím rozdílem, že uplatňujeme pravidla následovně:

0 + 1 = 1
1 + 0 = 1
0 + 0 = 0
1 + 1 = 10
1 + 1 + 1 = 11 (specifický případ, kdy sčítáme dvě jedničky nad sebou a schovali jsme si jedničku z předchozího řádu)

Dobře je to vysvětlené na tomto videu.


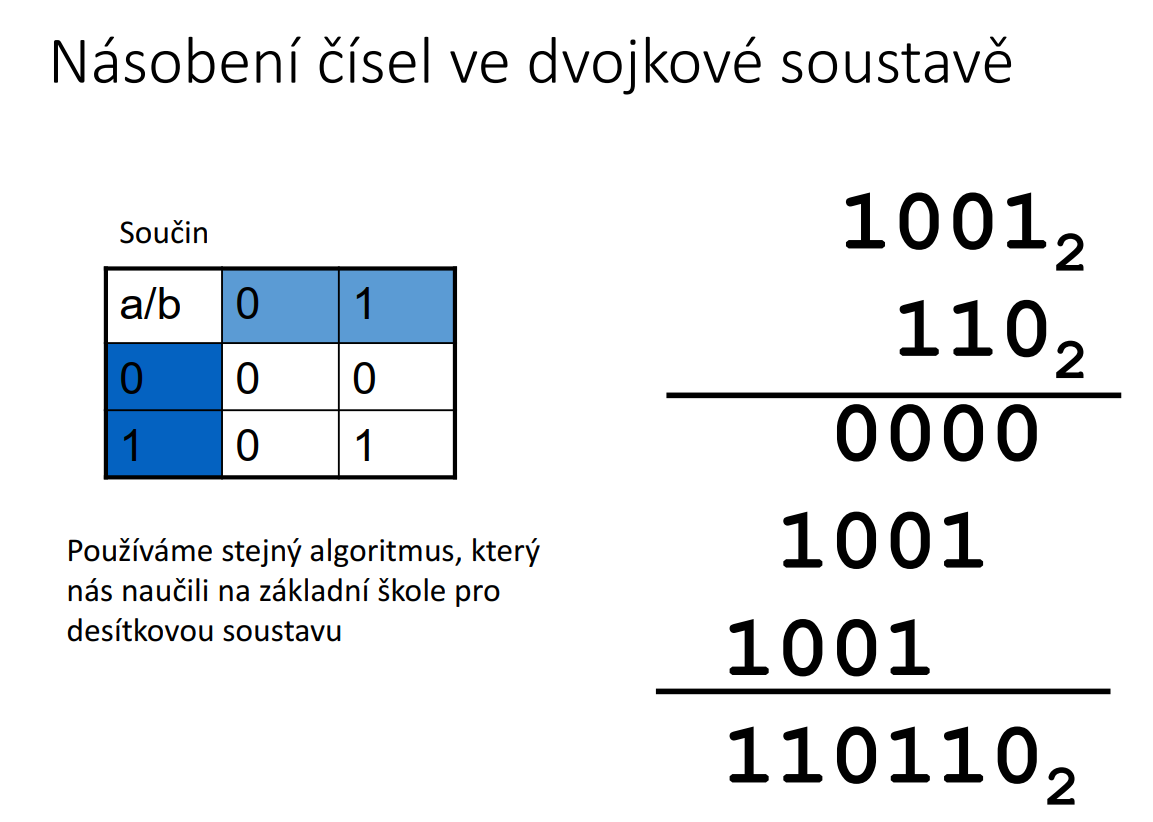obr. 4: Násobení v binární soustavě
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.

Opět je to stejné, jako násobení v decimální soustavě, řídíme se pravidly dle tabulky z obrázku.

0 * 0 = 0
1 * 0 = 0
0 * 1 = 0
1 * 1 = 1


obr. 5: Dělení v binární soustavě
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.

Dělení je o něco složitější, byť používáme stejnou metodu jako v desítkové soustavě. Postupujeme dělencem dokud nedojdeme k řádu, do nějž se vejde dělitel. Následně dělitel odečteme a k odečtu připisujeme další řády, dokud se nám tam dělitel opět nevejde.

Pokud se nám dělitel vejde do dělence, napíšeme 1, jinak 0.

Jiný příklad dělení:


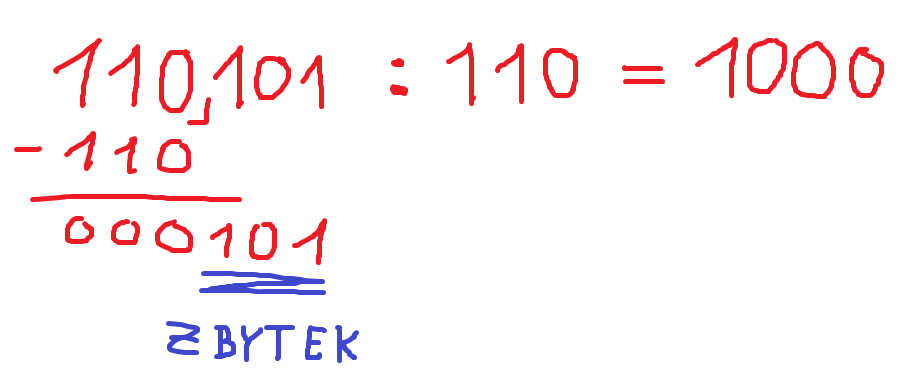obr. 6: Dělení v binární soustavě
zdroj: TRTÍLEK, Ondřej. Vlastní zpracování. České Budějovice, 2023.

Za každý přidaný řád (modře podtržený) dopisujeme do výsledku 0, dokud nedojdeme na konec dělence. Poté vyhodnotíme, zda se tam dělitel vejde či nikoli. pokud nikoli, tak jej považujeme za zbytek.

Vždy si můžeme převést čísla do decimální soustavy a zkontrolovat. 
Zde je to 53 : 6. Toto vyjde 8 se zbytkem 5.

Hexadecimální soustava


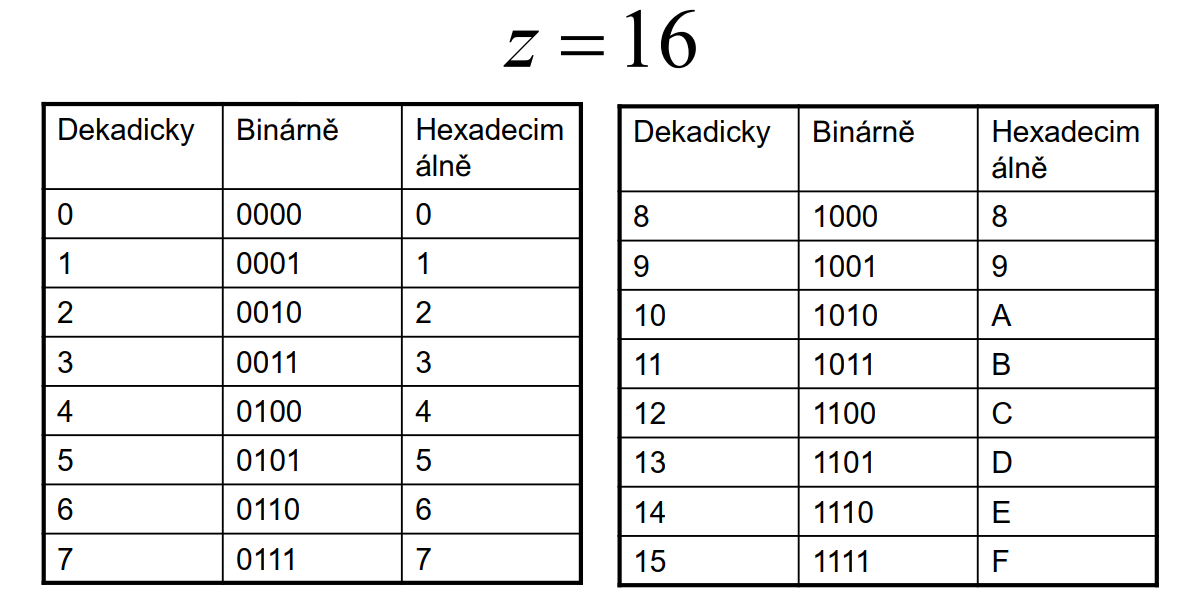obr. 7: Hexadecimální soustava
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.

Příklady v hexadecimální soustavě

$78FF$ $\Rightarrow$ $15 * 16^0 + 15 * 16^1 + 8 * 16^2 + 7 * 16^3$ $\Rightarrow$ $15 + 240 + 8 * 256 + 7 * 4096$ $\Rightarrow$ $255 + 2048 + 28672$ $\Rightarrow$ $30 975_{10}$

$A5$ $\Rightarrow$ $5 * 16^0 + 10 * 16^1$ $\Rightarrow$ $165_{10}$

Příbuzné soustavy a převody

Příbuzné soustavy jsou takové soustavy, kde základ jedné soustavy je mocninou základu druhé soustavy.

Binární, čtyřková, oktální, hexadecimální.

Decimální, stovková, tisícová soustava.

Tedy, budu-li převádět z hexadecimální do binární, rozepíšu jednotlivé znaky do 4 bitů. Budu-li převádět z binární do hexadecimální, tak si bity rozdělím právě po 4.

Začínám vždy zprava, abych mohl případně poslední čtveřici doplnit o 0.

$AC35$ $\Rightarrow$ $1010 | 1100 | 0011 | 0101$ $1001110011011$ $\Rightarrow$ $0001 | 0011 | 1001 | 1011$ $\Rightarrow$ $139B$

U čtyřkové soustavy vytvářím dvojice a u osmičkové soustavy trojice (při převodu do bináru zapisujeme daná čísla 3 respektive 2 bity).

$750_8$ $\Rightarrow$ $111 | 101 | 000_2$
$2131_4$ $\Rightarrow$ $10 | 01 | 11 | 01_2$

$100111101_2$ $\Rightarrow$ $100 | 111 | 101$ $\Rightarrow$ $475_8$
$1110101_2$ $\Rightarrow$ $01 | 11 | 01 | 01$ $\Rightarrow$ $1311_4$

Kódování znaků

Znak kódu je znak abecedy zapsaný v binární podobě, přičemž se pro zápis používají stanovená pravidla/standardy: ASCII, UTF-8, UTF-16, UTF-32 nebo Windows-1250 (pro kódování češtin na systémech Windows). Znakových sad je však mnoho.

ASCII

Nejzákladnější znakovou sadou je tzv. ASCII tabulka (American Standard Code for Information Interchange). Původní tabulka obsahuje 128 platných znaků kódovaných pomocí 7 bitů v rozsahu (0-127). Nezohledňuje diakritiku.

Tabulka obsahuje jednotlivé znaky, jejich číselnou hodnotu v decimální soustavě a v hexadecimální. Případně jen v hexadecimální (viz obrázek níže).


obr. 8: ASCII tabulka
zdroj: ASCII. In: Wikipedie Otevřená Encyklopedie [online]. 2008 [cit. 2023-05-11]. Dostupné z: https://upload.wikimedia.org/wikipedia/commons/4/4f/ASCII_Code_Chart.svg.

Nejprve označíme řádek, poté sloupec, tím dostaneme hexadecimální kód znaku a posléze jej převedeme na binární.

$k$ - $6B_{16}$ - $01101011_2$
$($ - $28_16$ - $00101000_2$

Každý znak má vlastní bitovou reprezentaci tvaru, tomuto se říká FONT. Font zobrazuje v grafické podobě znak/symbol.

UTF (Unicode)

Jednotlivé standardy UTF nám říkají kolika bity se jednotlivé znaky kódují. Jestli 8, 16 nebo 32 bity.

znak $B$
$0x42$ - UFT-8
$0x0042$ - UFT-16
$0x00000042$ - UFT-32

Reprezentace čísel se znaménkem a floating

Řádová mřížka Popisuje formát zobrazených čísel v počítači. Používá se z důvodu omezení při zobrazení čísel na menší rozsah (např. 1 bytu). Šířky řádových mřížek mohou být 8, 16, 32 či 64 bitů.

V závislosti na umístění řádové čárky určujeme rozsah zobrazitelných řádů čísla:

$n$ nejvyšší (MSB - Most Significant Bit)
$m$ nejnižší (LSB - Least Significant Bit)


obr. 9: Binární řádová mřížka zachycující hodnotu 001011,01
zdroj: HALUZA, Pavel, Jiří RYBIČKA a Tomáš HÁLA. Úvod do informatiky [online]. Brno: KONVOJ, spol. s.r.o, 2018 [cit. 2023-05-11]. ISBN 978-80-7302-174-0. Dostupné z: https://www.konvoj.cz/Nakladatelstvi/Knihy/100289-haluza-rybicka-hala-scriptum-43-uvod-do-informatiky/100289-uvod-do-informatiky.pdf

Vlastnosti mřížky

délka mřížky - vyjadřuje počet rozlišitelných hodnot (řádů), značíme $l$
jednotka - představuje nejmenší kladné zobrazitelné číslo, značíme $\varepsilon$
modul - představuje nejmenší číslo, které již zobrazitelné NENI, značíme $M$ nebo $Z$
pozice řádové čárky (může být plovoucí či pevná)

Operační paměť počítače rozdělujeme na adresovatelné jednotky o velikosti 1 Byte (slabiky). Délka řádové mřížky je proto vždy celým násobkem slabik.

Pro řádovou mřížku platí dále následující obecná pravidla:

$l = m + n + 1$
$\varepsilon = z^{-m}$, je to číslo, které má jedničku pouze v nejnižším řádu
$Z = 2^{n+1}$, jedná se o číslo, které má jedničku v řádu, který již není v mřížce obsažen

Overflow a Underflow

Overflow - přetečení Je-li délka řádové mřížky menší, než počet řádů čísla, které chceme do mřížky vložit, nebude toto číslo v mřížce zobrazitelné. Uloží se jen ty řády, které se do mřížky vejdou, zbytek řádů bude ignorován.

Při přetečení dojde ke ztrátě přesnosti čísla. Nevadí to tolik u ignorovaných nízkých řádů, ale ztráta nejvyšších řádů čísla znamená úplné znehodnocení číselného údaje.

K přetečení může dojít zejména při sčítání operandů se stejnými znaménky (odečítání s různými znaménky).

Underflow - podtečení Číslo je pro řádovou mřížku velmi malé, blíží se nule (je daleko za řádovou čárkou). Do řádové mřížky jej posléze zapíšeme jako 0, čímž dojde k zaokrouhlení a zkreslení.

Reprezentace záporných čísel

Problémem reprezentace čísel v počítači je binární zápis znaménka. Existují tří způsoby kódování pro práci se znaménkem:

Přímý kód
Aditivní kódování
Doplňkové kódování

Přímý kód - sign magnitude

Forma zápisu je pro člověka čitelná. Nicméně HW pro zpracování takového kódu by byl zbytečně pomalý a složitý.

znaménko je reprezentováno tzv. znaménkovým bitem (nejvyšším řádem mřížky)
nabývá 0 je-li číslo kladné a 1 je-li číslo záporné (nahrazuje znaménko -)


obr. 10: Reprezentace 4 bitových čísel se znaménkem v přímém kódu
zdroj: HALUZA, Pavel, Jiří RYBIČKA a Tomáš HÁLA. Úvod do informatiky [online]. Brno: KONVOJ, spol. s.r.o, 2018 [cit. 2023-05-11]. ISBN 978-80-7302-174-0. Dostupné z: https://www.konvoj.cz/Nakladatelstvi/Knihy/100289-haluza-rybicka-hala-scriptum-43-uvod-do-informatiky/100289-uvod-do-informatiky.pdf

kladná čísla rostou zleva
záporná rostou zprava
dvojí vyjádření 0, rovněž platí $-0 > 0$
původní n bity pro vyjádření čísla jsou sníženy na $n -1$, protože jeden bit je na znaménko
zobrazíme tedy $2^{n -1}$ hodnot
každé zobrazené číslo, ale nemusí mít znaménko
umíme zde zobrazit rozsah $-2^{n-1} + 1$ až $2^{n-1} - 1$

Příklad Vyjádření čísla -53 na 8 bitech se znaménkem:

převedeme do bináru $110101$
doplníme zleva nulami do celé délky mřížky \(00110101)
upravíme znaménkový bit
posloupnost je: $10110101$

Inverzní kód - one's complement (jedničkový doplněk)

používáme pro hledání reprezentace čísla v binárním doplňkovém kódu
kladná čísla jsou beze změny
záporná čísla mají svůj doplněk do jedničky
doplněk 0 je jednička
doplněk 1 je nula
provádíme inverzi všech bitů čísla


obr. 11: Reprezentace 4 bitových čísel se znaménkem v inverzním kódu
zdroj: HALUZA, Pavel, Jiří RYBIČKA a Tomáš HÁLA. Úvod do informatiky [online]. Brno: KONVOJ, spol. s.r.o, 2018 [cit. 2023-05-11]. ISBN 978-80-7302-174-0. Dostupné z: https://www.konvoj.cz/Nakladatelstvi/Knihy/100289-haluza-rybicka-hala-scriptum-43-uvod-do-informatiky/100289-uvod-do-informatiky.pdf

zachováváme relaci mezi kladnými a zápornými
oboje roste zleva doprava
reprezentace i zobrazovaný rozsah je stejná jako v přímém kódu

Příklad Vyjádření čísla -53 na 8 bitech v inverzním kódu:

převedeme do bináru $110101$
doplníme zleva nulami do celé délky mřížky \(00110101)
provedeme inverzi všech bitů
posloupnost je: $11001010$

Doplňkový kód - two's complement (dvojkový doplněk)

odstraňuje dvojí reprezentaci 0
tvoří se stejně jako inverzní kód
záporné číslo je reprezentováno přičtením jedničky
nejpoužívanější číselný kód pro celá čísla a pro většinu operací na moderních strojích


obr. 11: Reprezentace 4 bitových čísel se znaménkem v doplňkovém kódu
zdroj: HALUZA, Pavel, Jiří RYBIČKA a Tomáš HÁLA. Úvod do informatiky [online]. Brno: KONVOJ, spol. s.r.o, 2018 [cit. 2023-05-11]. ISBN 978-80-7302-174-0. Dostupné z: https://www.konvoj.cz/Nakladatelstvi/Knihy/100289-haluza-rybicka-hala-scriptum-43-uvod-do-informatiky/100289-uvod-do-informatiky.pdf

Příklad Vyjádření čísla -53 na 8 bitech v doplňkovém kódu:

převedeme do bináru $110101$
doplníme zleva nulami do celé délky mřížky \(00110101)
provedeme inverzi všech bitů
posloupnost je: $11001010$
K výsledku přičteme jedničku
Výsledek: $11001011$

lze to vyjádřit také tak, že si vypočítáme maximální hodnotu na 8 bitech $2^8$
od této hodnoty odečteme (resp. přičteme k ní) číslo -53
výsledek je 203
převedeme jej do bináru
binární hodnota tohoto čísla odpovídá právě číslu -53
nemůže dojít k záměně, protože zobrazujeme pouze hodnoty od -127 do 128
interval zobrazitelných hodnot je $-2^{n-1}$ až $2^{n-1} - 1$

Aditivní kód (biased)

0 posunujeme přibližně do poloviny intervalu
ke každému číslu přičteme konstantu
interval zobrazených čísel je $-2^{n-1}$ až $2^{n-1} - 1$


obr. 11: Reprezentace 4 bitových čísel se znaménkem v aditivním kódu
zdroj: HALUZA, Pavel, Jiří RYBIČKA a Tomáš HÁLA. Úvod do informatiky [online]. Brno: KONVOJ, spol. s.r.o, 2018 [cit. 2023-05-11]. ISBN 978-80-7302-174-0. Dostupné z: https://www.konvoj.cz/Nakladatelstvi/Knihy/100289-haluza-rybicka-hala-scriptum-43-uvod-do-informatiky/100289-uvod-do-informatiky.pdf

kladná čísla mají v MSB jedničku
záporná mají v MSB nulu

BCD - binary coded decimal

používá se v kalkulačkách, měřících přístrojích
princip je uložení čísel desítkové soustavy do půlslabiky (4 bity)
jiné číslice se nevyskytují
zhuštěný tvar BCD - v jedné slabice jsou dvě čísla
nezhuštěný tvar BCD - v jedné slabice je jedno číslo
znaménko $+$ je často zachyceno jako 1010
znaménko $-$ jako 1011
znaménko tedy zabírá stejný počet bitů jako číslice

Příklad Vyjádření čísla 38 v BCD:

3 do bináru $0011$
8 do bináru $1000$
nezhuštěný tvar na 2 bajtech: 00000011 00001000
zhuštěný tvar na 1 bajtu: $00111000$

Floating - racionální čísla s plovoucí čárkou

tento zápis standardizuje norma IEEE 754
jedná se o tzv. semilogaritmický tvar, jinak též vědecká notace (viz zde)

POJMY

mantisa - upravuje číslo do tvaru, ve kterém je čárka umístěna za první nenulovou číslici, přičemž platí $1 \leq m < z$
m je mantisa, z je základ soustavy
exponent - vyjadřuje počet řádů, o které bylo nutné čárku posunout
kladný exponent (posun doleva), záporný (posun doprava)
každé racionální číslo pak lze vyjádřit součinem mantisy a základu soustavy umocněného exponentem
0,00004945 $\Rightarrow$ $4,945 * 10^{-5}$

Paměťový prostor pro vyjádření racionálních čísel s floatingem je rozdělen na 3 části: znamenko, mantisa a exponent.

Exponent se vyjádří v aditivním kódu s posunem o $2^{n-1} - 1$. Mantisa by vždy začínala jedničkou (v bináru je každá nenulová číslice jednička). Tato jedničma se neukládá, jde o tzv. skrytý bit. Ušetřené místo slouží k zobrazení dalšího bitu zlomkové části - zvyšuje se přesnost zobrazení čísla.

3 formáty zobrazení racionálních čísel s floatingem

single precision (jednoduchá přesnost): 32 bitů celkem. 1 bit pro znaménko, 8 bitů exponent, zbytek je mantisa (23 bitů)
double precision (dvojitá přesnost): 64 bitů celkem, 1 bit znaménko, 11 bitů pro exponent a zbytek pro mantisu (52 bitů)
extended precision (rozšířená přesnost): 80 bitů celkem, 1 bit znaméneko, 15 bitů exponent, zbytek je mantisa (64 bitů)

Algoritmus převodu

Absolutní hodnotu čísla převedeme do bináru
Normalizujeme výsledek (mantisu zachytíme binárně), expnent decimálně
Exponent převedeme do aditivního kódu posunem o konstantu
Zkrátíme mantisu na požadovanou přesnost (řešíme pouze bity za řádovou čárkou)
Nastavíme hodnotu znaménkového bitu

Příklad

máme číslo 64.2 - single precision
převedeme do bináru
$64 \Rightarrow 1000000$
$0.2 \Rightarrow 0.001100110011...$
$1000000.001100110011...$
výsledek normalizujeme na: $1.000000001100110011... * 2^6$
upravíme exponent přičtením konstanty 127 ($2^{8-1} - 1)$, exponent je 8 bitový, tedy n by mělo být 8 (?)
získáme tím číslo 133 (6 + 127)
převedeme do binárního kódu (10000101)
vezmeme část mantisi (za řádovou čárkou) a zkrátíme na požadovaných 23 bitů
dostaneme posloupnost 00000000110011001100110
nastavíme znaménkový bit na 0 (máme kladný exponent)
složíme dohromady
VÝSLEDEK: |0|10000101|00000000110011001100110|

ZDROJE

SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.
HALUZA, Pavel, Jiří RYBIČKA a Tomáš HÁLA. Úvod do informatiky [online]. Brno: KONVOJ, spol. s.r.o, 2018 [cit. 2023-05-11]. ISBN 978-80-7302-174-0. Dostupné z: https://www.konvoj.cz/Nakladatelstvi/Knihy/100289-haluza-rybicka-hala-scriptum-43-uvod-do-informatiky/100289-uvod-do-informatiky.pdf
Přispěvatelé Wikipedie, Pohyblivá řádová čárka [online], Wikipedie: Otevřená encyklopedie, c2021, Datum poslední revize 30. 09. 2021, 15:28 UTC, [citováno 12. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Pohybliv%C3%A1_%C5%99%C3%A1dov%C3%A1_%C4%8D%C3%A1rka&oldid=20512652
Přispěvatelé Wikipedie, Kódování znaků [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 8. 03. 2023, 09:17 UTC, [citováno 12. 05. 2023] https://cs.wikipedia.org/w/index.php?title=K%C3%B3dov%C3%A1n%C3%AD_znak%C5%AF&oldid=22525989

Kombinační a sekvenční logické obvody

Kombinační a sekvenční logické obvody, formální popis logických obvodů booleovskými funkcemi a konečnými automaty.

Základem kombinačních i sekvenčních obvodů jsou logická hradla. Z těch se výše zmíněné skládají.


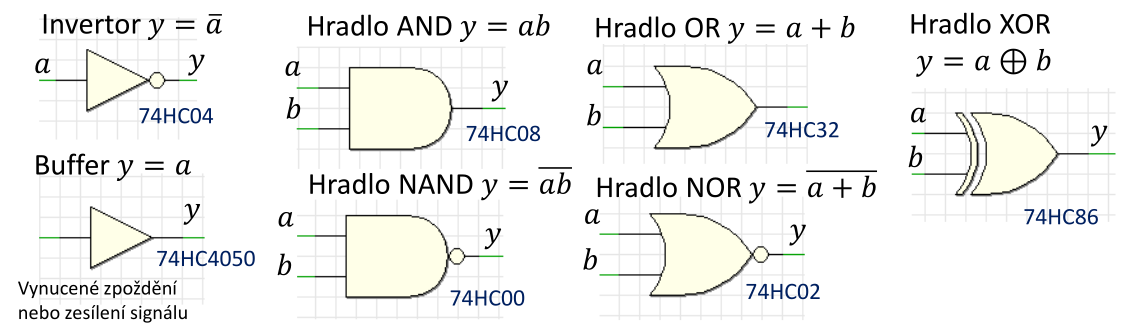obr. 1: Běžná logická hradla (uvedené identifikátory `74HCxx` označují běžně dostupné integrované obvody s těmito hradly)
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Popis booleovskými funkcemi

Booleovská proměnná je taková proměnná, která může nabývat pouze dvou hodnot, a to 0 a 1.

Booleovská funkce je taková funkce, která přijímá jako vstupy a vrací jako výstupy pouze booleovské proměnné. Platí, že pro $n$ booleovských proměnných existuje $ 2^{2^n} $ booleovských funkcí (např. pro 2 proměnné máme celkem 4 kombinace vstupů, kterým odpovídá 16 funkcí).


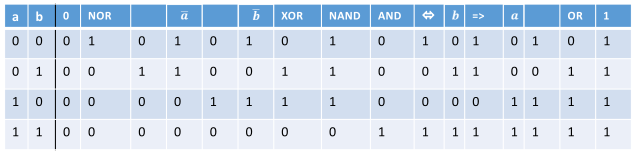obr. 2: Boolovská funkce dvou proměnných
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Vzhledem k tomu, že logické obvody pracují pouze s booleovskými proměnnými (jejich vstupy a výstupy) a obsahují logická hradla (ta reprezentují logické operace), můžeme je považovat za elektronické formy booleovských funkcí a tedy je pomocí nich popisovat.

Pravdivostní tabulka

Základní pomůckou pro reprezentaci logických obvodů pomocí booleovských funkcí je pravdivostní tabulka. Ta obsahuje sloupce pro všechny vstupní i výstupní proměnné a řádky pro všechny kombinace hodnot vstupních proměnných. Např. následující tabulka pro funkci $ y = a + b $.

a	b	y
0	0	0
0	1	1
1	0	1
1	1	1

Úplné normální formy

Z pravdivostní tabulky vychází další důležitý pojem a také další krok, kterým jsou úplné normální formy. Máme dvě a jsou definovány takto:

Úplná normální disjunktní forma (ÚNDF) - součet (disjunkce) mintermů (pouze ze řádků, kde je výstup roven 1)
- minterm - součin (konjunkce) všech proměnných v řádku (ty, které mají hodnotu 1, jsou přímé, s hodnotou 0 negované); tedy pro $ a, b, c = 0, 1, 0$ to bude $ \neg a \cdot b \cdot \neg c $
Úplná normální konjunktivní forma (ÚNKF) - součin (konjunkce) maxtermů (pouze ze řádků, kde je výstup roven 0)
- maxterm - součet (disjunkce) všech proměnných v řádku (ty, které mají hodnotu 0, jsou přímé, s hodnotou 1 negované); tedy pro $ a, b, c = 0, 1, 0$ to bude $ a + \neg b + c $

Pro výše uvedenou tabulku by NF vypadali takto:

ÚNDF - $ y = (\neg a \cdot b) + (a \cdot \neg b) + (a \cdot b) $
ÚNKF - $ y = a + b $

Minimalizace

Úplné normální formy jsou sice popisem odpovídajících obvodů, ale zpravidla nejsou popisem ideálním. Abychom dosáhli ideálního, tedy co nejmenšího popisu, musíme je minimalizovat. K tomu můžeme využít následující metody:

algebraická minimalizace - úprava výrazu využitím zákonů booleovy algebry (poměrně náročné)
Karnaughovy mapy - postup zde (doporučuji)
algoritmus Quine-McCluskey

Kombinační obvody

Kombinační obvody jsou takové logické obvody, u kterých aktuální stav výstupů závisí pouze na okamžitém stavu vstupů, nikoliv an předchozích stavech (není zde žádná paměť).

Půlsčítačka

Velmi jednoduchý obvod, který je schopen sečíst dvě jednobitová čísla. Omezením je, že neumí přijímat carry bit z nižšího řádu (to je problém, když děláme vícebitové sčítačky - řetězení).


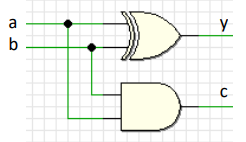obr. 1: Schéma půlsčítačky
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Význam jednotlivých vstupů a výstupů:

a - vstupní bit
b - vstupní bit
y - výstupní bit (výsledek)
c - carry bit (symbolizuje přetečení do vyššího řádu)

Pravdivostní tabulka

a	b	y	c
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Booleovské funkce

\[ y = a \oplus b \\ c = a \cdot b \]

Úplná sčítačka

Stejná jako půlsčítačka, ale umí přijímat carry bit z nižšího řádu.


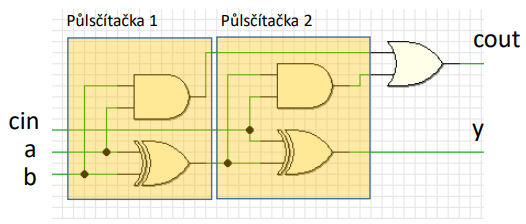obr. 2: Schéma úplné sčítačky
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Význam jednotlivých vstupů a výstupů:

a - vstupní bit
b - vstupní bit
cin - carry bit z předešlého řádu
y - výstupní bit (výsledek)
cout - výstupní carry bit (symbolizuje přetečení do vyššího řádu)

Pravdivostní tabulka

a	b	c_in	y	c_out
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Booleovské funkce

\[ y = a \oplus b \oplus c_{in} \\ c = a \cdot b + (a \oplus b) \cdot c_{in} \]

Vícebitová sčítačka

Jedná se o zřetězení jednobitových plných sčítaček.


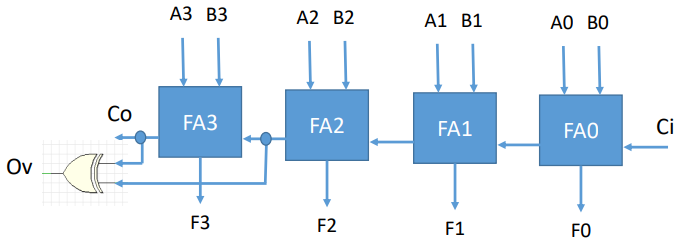obr. 3: Schéma čtyřbitové sčítačky
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Význam jednotlivých vstupů a výstupů:

A0...3 - vstupní bity
B0...3 - vstupní bity
Ci - carry bit z předešlé sčítačky (je-li nějaká)
F0...3 - výstupní bit (výsledek)
Ov - identifikátor přetečení, pro čísla v doplňkovém kódu

Multiplexor

Multiplexor (často zkracovaný jako mux) funguje jako elektronický přepínač. Tím je myšleno, že za pomoci řídicích vodičů vybírá jeden ze vstupů, a ten přivádí na výstup. Např. máme čtyřvstupový mux, tedy máme dva řídicí vodiče a podle toho, jaká hodnota je na ně přivedena (viz pravdivostní tabulka) se jeden ze vstupů přivede na výstup.

Opakem je demultiplexor (demux), který dělá přesný opak - pomocí řídicích vstupů určujeme, na který výstup přepneme vstup (ten je jeden).


obr. 4: Schéma muxu
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Význam jednotlivých vstupů a výstupů:

A...D - vstupy, mezi kterými přepínáme
S - řídicí vodiče (červeně označené číslo udává jejich počet)
Y - výstup

Pravdivostní tabulka

Pro čtyřvstupový mux. X zde znamená, že na hodnotě nezáleží.

A	B	C	D	S1	S2	Y
X	X	X	X	0	0	A
X	X	X	X	0	1	B
X	X	X	X	1	0	C
X	X	X	X	1	1	D

Posuvy

Bitové posuvy se provádějí tak, že před každý výstup je předřazen jeden mux, který přepíná mezi odpovídajícím vstupem a vstupem na vedlejší pozici (podle toho, kam posuv směřuje). Všechny muxy (pro všechny bity) mají společné řízení (= přepínání mezi normálním výstupem, nebo posuvem).


obr. 5: Levý posuv, pravý posuv
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Komparátor

Porovnává hodnoty vstupů a podle typu upravuje výstup. Typ odpovídá operaci, kterou provádí, tedy: =, < a >. Výstup má hodnotu podle toho, jestli je splněna podmínka daná operací.


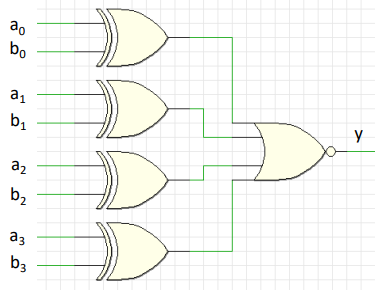obr. 6: Schéma komparátoru '=' (4 b)
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Význam jednotlivých vstupů a výstupů:

a0...3 - vstupní bity
b0...3 - vstupní bity
y - výstup (výsledek)

Porovnává se vždy odpovídající dvojice bitů, tedy např. a0 s b0.

Pravdivostní tabulka

By byla vzhledem k počtu vstupů dosti velká a lze ji jednoduše odvodit ze zapojení či booleovské funkce, nebude zde tedy uvedena.

Booleovské funkce

Pro typ =.

\[ y = \neg (a_0 \oplus b_0 + ... + a_n \oplus b_n) \]

Kde $ n $ je počet bitů komparátoru (respektive počet dvojic vstupů).

Násobička

Násobička je soustava $ n^2 $ sčítaček (kde $ n $ je počet bitů jednoho vstupu - činitele), které pracují sériově (tedy postupně → dochází k poměrně velkému zpoždění). Výstup má $ 2 \cdot n $ bitů.

Ne všechny procesory mají násobičku (a tedy instrukci pro násobení). Kde chybí, je nutné násobení provádět opakovaným sčítáním a bitovými posuvy (pomocí kódu v jazyce symbolických adres).


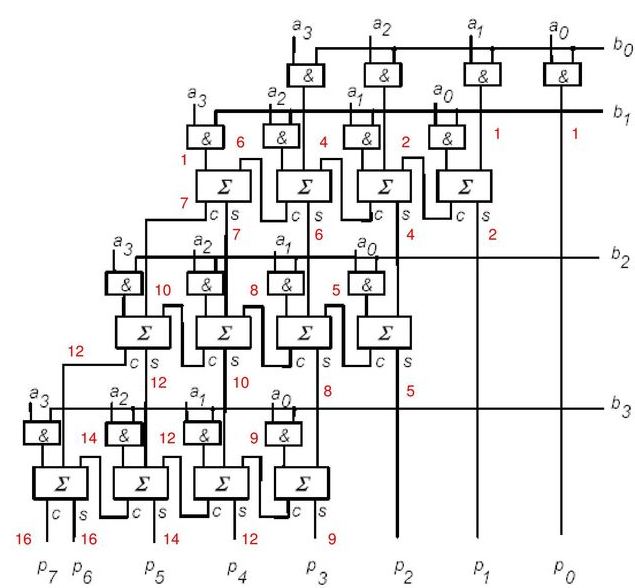obr. 7: Schéma násobičky (4 b); každý řádek je jedna sčítačka
zdroj: Násobičky, Boothovo překódování: Demonstrační cvičení 7 [online]. [cit. 2023-05-16]. Dostupné z: https://docplayer.cz/17659319-Nasobicky-boothovo-prekodovani-demonstracni-cviceni-7.html

Význam jednotlivých vstupů a výstupů:

a0...3 - vstupní bity prvního činitele
b0...3 - vstupní bity druhého činitele
P0...7 - výstupní bity (výsledek)

Sekvenční obvody

Sekvenční obvody, na rozdíl od kombinačních, pracují s předešlým stavem, jsou tedy schopny udržovat hodnotu v čase.

Pro práci se sekvenčními obvody je nutné nejprve vysvětlit, co je to tzv. hodinový signál. Jedná se o digitální (nespojitý jak v čase, tak v hodnotě) signál s pevně danou frekvencí a obvykle střídou 50% (to však není pravidlo). Sekvenční obvody jej využívají k informování o tom, kdy mají vykonat svou činnost.

Jeho frekvence udává rychlost činnosti daného obvodu (např. u PC mluvíme o rychlosti procesoru).

R-S klopný obvod

Synchronní hladinový R-S KO (klopný obvod) je nejjednodušším synchronním KO. Další KO se z něj odvozují. Funguje jako dočasná paměť (uchovává hodnoty na výstupu, do příchodu nového pulzu).

synchronní zde znamená, že využívá hodinový signál (může být i asynchronní = bez hodinového signálu).
hladinový znamená, že vstupní hodnoty se mohou měnit po celou dobu, co je CLK v log. 1 (alternativou jsou hranové KO, ty jsou však konstrukčně náročnější)


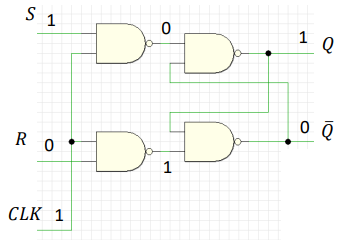obr. 8: Schéma synchronního hladinového R-S KO
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Pravdivostní tabulka

X znamená, že na hodnotě nezáleží. Q a Q (negované) znamená předešlou hodnotu (tedy že nedošlo ke změně) = paměťová funkce.

CLK	R (reset)	S (set)	Q	Q (negované)
0	X	X	Q	Q (negované)
1	0	0	Q	Q (negované)
1	0	1	1	0
1	1	0	0	1
1	1	1	nepredikovatelný	nepredikovatelný

Poslední řádek je tzv. zakázaný stav, který by neměl nikdy nastat (výstupy jsou totiž nepredikovatelné). Často se přidávají ochrany, aby se mu zabránilo.

D klopný obvod

Vylepšený R-S KO (dostaneme jej tak, že na vstup R přivedeme negovanou hodnotu S; zde popsaná varianta má však změn více). Používá se jako jednobitová paměť (hodí se k tomu lépe než R-S).


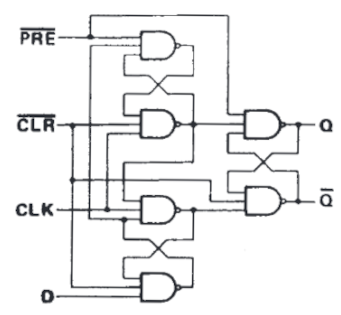obr. 9: Schéma hranového D KO
zdroj: DUAL D-TYPE EDGE TRIGGERED FLIP-FLOPS WIDTH PRESET AND CLEAR, datasheet, Texas Instruments Incorporated, 1988.

Význam jednotlivých vstupů a výstupů:

PRE - preset - nastaví Q na log. 1 (je asynchronní, tedy pracuje bez ohledu na hodiny), používá se k inicializaci
CLR - clear - nastaví Q na log. 0 (je také asynchronní), rovněž se používá k inicializaci
CLK - hodinový signál
D - datový vstup (při hodinové 1 se přenese na Q)
Q - výstup
Q (negované) - negovaný výstup

Pravdivostní tabulka

X znamená, že na hodnotě nezáleží. Q a Q (negované) znamená předešlou hodnotu (tedy že nedošlo ke změně) = paměťová funkce.

CLK	PRE (negované)	CLR (negované)	D	Q	Q (negované)
X	0	1	X	0	1
X	1	0	X	1	0
0	0	0	X	Q	Q (negované)
1	0	0	0	0	1
1	0	0	1	1	0

Registry

Jednobitový registr se synchronním zápisem a asynchronním nulováním

Jedná se o D KO doplněný o mux, který přepíná mezi aktuálním výstupem a vstupem (novou hodnotou). K přepínání dochází na základě hodnoty vstupu write (avšak jen ve chvíli kdy dojde k log. 1 na CLK).


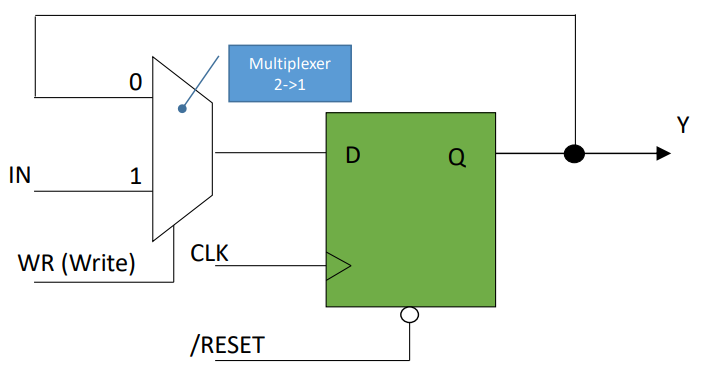obr. 10: Jednobitový registr se synchronním zápisem a asynchronním nulováním
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Význam jednotlivých vstupů a výstupů:

IN - vstup
WR - write - povoluje zápis aktuální vstupní hodnoty na výstup
CLK - hodinový signál
RESET - vynuluje uloženou hodnotu (je negovaný)
Y - výstup

Vícebitový (paralelní) registr

Jedná se o více jednobitových registrů, které mají společné hodiny a WR. Takto si můžeme představit registry v CPU.


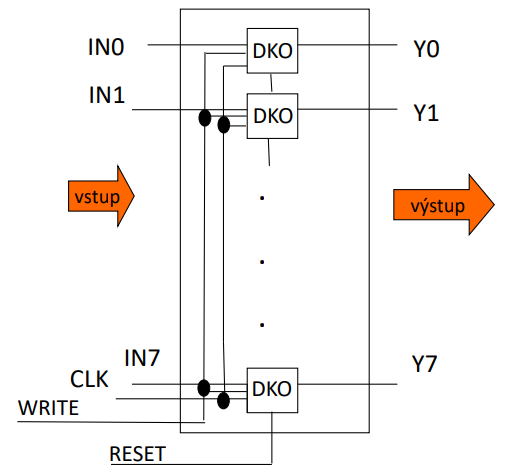obr. 11: Osmibitový paralelní registr
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Posuvný registr

Slouží k serializaci a deserializaci dat.


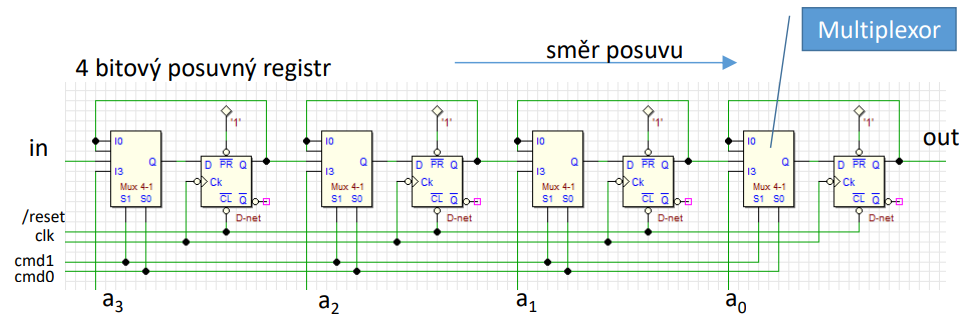obr. 121: Čtyřbitový posuvný registr
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Význam jednotlivých vstupů a výstupů:

IN - sériový vstup (používá se pro postupné přikládání hodnoty; při deserializaci)
a0...3 - paralelní vstupy (pro okamžité přiložení hodnoty; pří serializaci)
reset - úvodní nastavení (negované)
clk - hodinový signál
cmd0,1 - slouží k nastavení aktivního vstupu (0, X - beze změny; 1, 0 - sériový; 1, 1 - paralelní)
OUT - sériový výstup (ještě by zde měly být paralelní výstupy - za každým KO)

Popis konečnými automaty

Sekvenční obvody lze též popsat pomocí konečných automatů. Jejich činností je totiž přijímat vstupy a na jejich základě podávat výstupy, což je s KA shodné.

Práce s takovými KA je shodná s klasickými KA. Jediným rozdílem je, že potřebujeme binárně zakódovat vstupy a výstupy (můžeme pracovat jen s booleovskými proměnnými).

Zdroje

Přispěvatelé Wikipedie, Kombinační obvod [online], Wikipedie: Otevřená encyklopedie, c2020, Datum poslední revize 23. 06. 2020, 08:32 UTC, [citováno 16. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Kombina%C4%8Dn%C3%AD_obvod&oldid=18753069
SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.
Přispěvatelé Wikipedie, Bistabilní klopný obvod [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 5. 11. 2022, 14:10 UTC, [citováno 16. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Bistabiln%C3%AD_klopn%C3%BD_obvod&oldid=21839873

Základní architektury počítačů

Architektura počítačů je technický obor zaměřený na návrh a konstrukci zařízení na zpracování dat (počítač). Zajišťuje:

stanovení vnitřní reprezentace dat a operací, které se s nimi budou provádět
specifikaci funkčních bloků (jednotek) počítače a jejich propojení
formát strojových instrukcí
způsob jak pracuje CPU a jakým způsobem přistupuje k paměti

Architektura počítače je tedy konkrétní způsob realizace počítače. Existují dvě základní koncepce konstrukce počítače:

Von Neumannova architektura:
- používá jednu sběrnici, na kterou jsou připojeny všechny aktivní prvky (procesor, paměť, vstupy a výstupy)
- činnost počítače je sekvenční (oproti harvardské) a je řízena řadičem. Řadič načítá jednu instrukci po druhé, dekóduje je a postupně je provádí
- každou instrukci lze rozdělit na jednodušší operace
- skládá se z:
  - řadiče - elektronická řídicí jednotka, realizovaná sekvenčním obvodem, která řídí činnost všech částí počítače. Toto řízení je prováděno pomocí řídicích signálů, které jsou zasílány jednotlivým modulům (dílčím částem počítače). Dílčí částí počítače je např. operační paměť, která rovněž obsahuje řadič, který je podřízen hlavnímu řadiči počítače, jenž je součástí CPU.
  - aritmeticko-logické jednotky (ALU) - provádí všechny aritmetické (např. sčítání, násobení, bitový posuv, …) a logické (logický součin, negace, …) výpočty. Operace jsou prováděny nad operandy s pevně daným rozsahem závislým na architektuře. Výpočty s libovolnou přesností je tak zapotřebí provádět pomocí softwarových knihoven.
  - vstupní/výstupní jednotka - zařizuje přenos dat mezi periferním zařízením nebo vnější pamětí a počítačem.


obr. 1: Von Neumannova architektura

Harvardská architektura:
- používá oddělenou paměť pro data a pro program
- může používat (pro čtení i zápis) paměť programu i paměť dat najednou - tzn. paralelně (oproti Von Neumannové architektuře)
- často se používá u jednočipových počítačů, malých vestavěných systémů (PDA, mobilní telefony a podobně) a především u signálových procesorů (DSP) u nichž dovoluje dosáhnout velké rychlosti zpracování dat


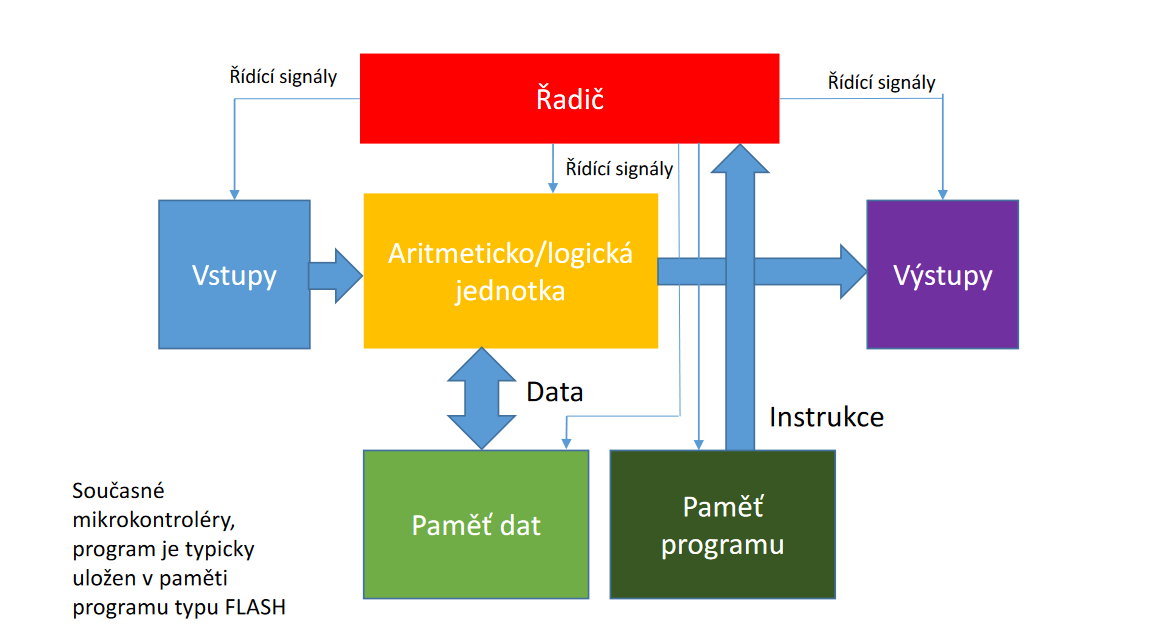obr. 2: Harvardská architektura

Architektura současného PC

Současné počítače nejsou konstruovány důsledně ani podle jednoho z těchto dvou základních schémat. Univerzální osobní počítače obsahují jen jednu paměť, do které se umisťují programy i zpracovávaná data.


obr. 3: Architektura současného PC

Procesor (CPU) - je základní elektronická jednotka, která umí vykonávat strojové instrukce (označení kódovaného příkazu pro provedení elementární operace procesoru), ze kterých je tvořen počítačový program a obsluhovat jeho vstupy a výstupy. Mezi hlavní součásti procesoru patří aritmeticko-logická jednotka, registry a řadič.

Registr procesoru má za úkol:

udržovat stav procesoru
sloužit o odkládání mezivýsledků
tvořit operandy aritmetických a logických operací

Citace

Wikipedie: Otevřená encyklopedie: Architektura počítače[online]. c2020 [citováno 16. 02. 2023]. Dostupný z WWW: https://cs.wikipedia.org/w/index.php?title=Architektura_po%C4%8D%C3%ADta%C4%8De&oldid=18604330
KUBA, Pavel. ARCHITEKTURA POČÍTAČŮ. Katedra informatiky, PřF, UJEP v Ústí nad Labem. Ústí nad Labem, 2016.

Instrukční cyklus počítače

Jednotlivé fáze zpracování instrukce. Pojem proudové zpracování (pipelinig) instrukcí.

V každém zařízení, které nazýváme počítačem, se nachází CPU. Toto CPU se skládá z několika základních částí, nutných pro vykonávání instrukčního cyklu.

Části CPU účastnící se instrukčního cyklu

Hodiny

Křemíkový krystal, který vibruje s určitou frekvencí. Jedna vibrace se nazývá tik. Počet tiků za vteřinu určuje frekvenci procesoru. S každým tikem CPU vykoná jednu část instrukčního cyklu.

Program counter (PC; čítač)

Jedná se o registr, ve kterém se nachází adresa právě vykonávané instrukce.

Instruction register (IT; instrukční registr)

Registr, ve kterém je uložena právě vykonávaná instrukce

Accumulator (akumulátor)

Jde o registr, ve kterém je uložen výsledek právě vykonávané instrukce (ne vždy ho CPU má; může místo něj použít jiný registr pro obecné použití).

Instrukce a data, se kterými procesor pracuje, se nacházejí v RAM. Každá instrukce má dvě části: instrukce samotná a adresa dat, se kterými pracuje


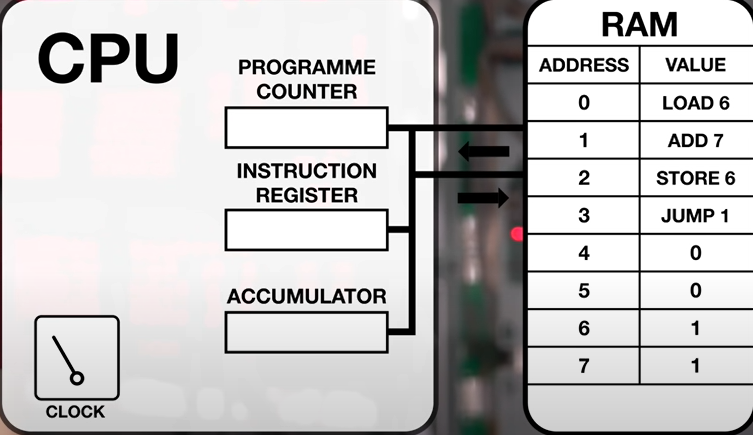obr. 1: Výchozí stav CPU před započetím instrukčního cyklu
Dostupné z: https://www.youtube.com/watch?v=Z5JC9Ve1sfI

Instrukční cyklus

Instrukční cyklus se skládá ze 3 částí. Fetch, Decode a Execute.

Fetch

První částí je získání instrukce na adrese čítače (PC) a natažení této instrukce do instrukčního registru.

Decode

Ve druhé části se instrukce dekóduje. Tedy CPU zjistí, co má instrukce dělat a kde se nachází hodnoty, se kterými má provádět operaci, jež instrukce definuje.

Execute

Nakonec CPU provede instrukci a výsledek instrukce uloží do akumulátoru. Adresa v PC se zvýší o 1 (pokud není dáno jinak právě vykonávanou instrukcí).

Příklad průběhu instrukčního cyklu

Čítač se nastaví na 0 (někde se začít musí).

První průchod

Hodiny tiknuly. CPU získá (fetchne) instrukci na adrese 0 a načte ji do instrukčního registru.
Hodiny tiknuly. CPU dekóduje instrukci v instrukčním registru. Zjistí tedy, že operace je LOAD a adresa je 6.
Hodiny tiknuly. CPU vykoná instrukci v instrukčním registru. Instrukce LOAD znamená načti. CPU tedy načte hodnotu z adresy 6. Tuto hodnotu uloží do akumulátoru. PC se inkrementuje o 1.


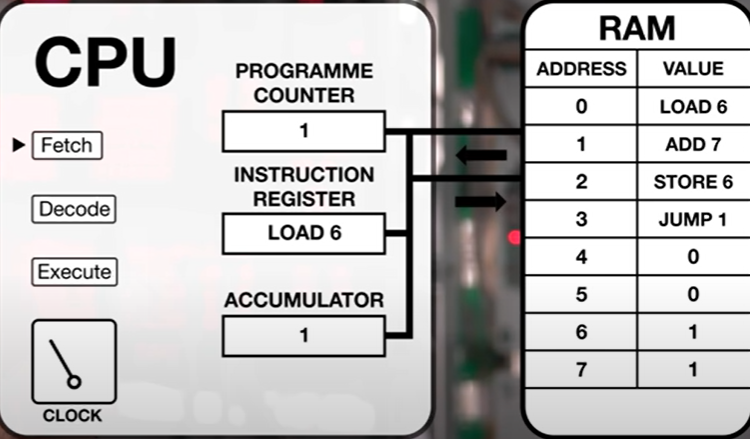obr. 2: Stav CPU a paměti po prvním průchodu instrukčním cyklem
Dostupné z: https://www.youtube.com/watch?v=Z5JC9Ve1sfI

Druhý průchod

Hodiny tiknuly. CPU získá (fetchne) instrukci na adrese 1 a načte ji do instrukčního registru.
Hodiny tiknuly. CPU dekóduje instrukci v instrukčním registru. Zjistí tedy, že operace je ADD a adresa je 7.
Hodiny tiknuly. CPU vykoná instrukci v instrukčním registru. Instrukce ADD znamená přidej. CPU tedy načte hodnotu z adresy 7. Tuto hodnotu přidá k hodnotě v akumulátoru. PC se inkrementuje o 1.


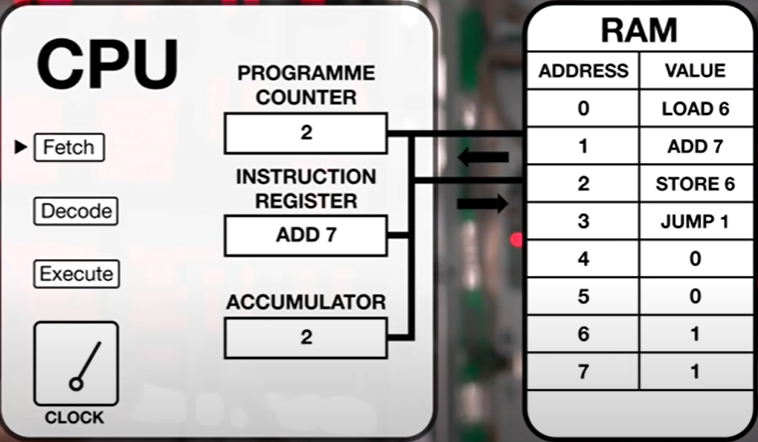obr. 3: Stav CPU a paměti po druhým průchodu instrukčním cyklem
Dostupné z: https://www.youtube.com/watch?v=Z5JC9Ve1sfI

Třetí průchod

Hodiny tiknuly. CPU získá (fetchne) instrukci na adrese 2 a načte ji do instrukčního registru.
Hodiny tiknuly. CPU dekóduje instrukci v instrukčním registru. Zjistí tedy, že operace je Store a adresa je 6.
Hodiny tiknuly. CPU vykoná instrukci v instrukčním registru. Instrukce Store znamená ulož. CPU tedy uloží hodnotu, co má v akumulátoru, do registru, jež se ukrývá pod adresou 6. Programme counter se inkrementuje o 1.


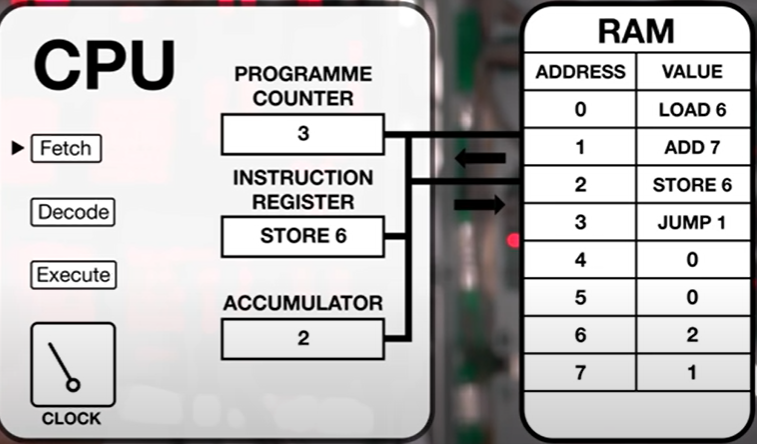obr. 4: Stav CPU a paměti po třetím průchodu instrukčním cyklem Dostupné z: https://www.youtube.com/watch?v=Z5JC9Ve1sfI

Čtvrtý průchod

Hodiny tiknuly. CPU získá (fetchne) instrukci na adrese 3 a načte ji do instrukčního registru.
Hodiny tiknuly. CPU dekóduje instrukci v instrukčním registru. Zjistí tedy, že operace je JMP a adresa je 1.
Hodiny tiknuly. CPU vykoná instrukci v instrukčním registru. Instrukce JMP znamená změň PC na. CPU tedy nastaví PC na adresu 1.


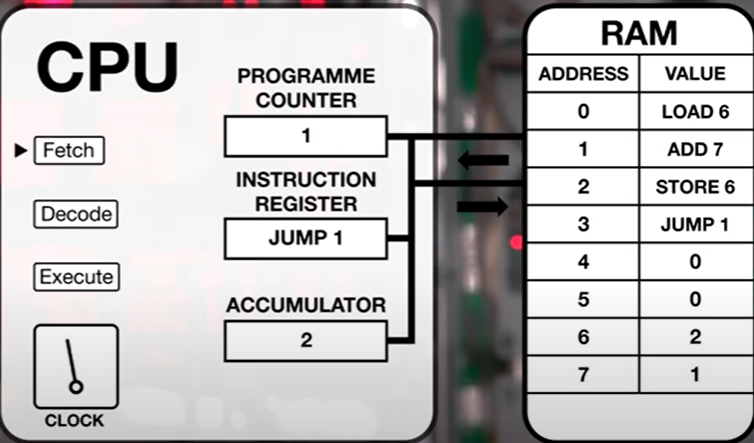obr. 5: Stav CPU a paměti po čtvrtém průchodu instrukčním cyklem
Dostupné z: https://www.youtube.com/watch?v=Z5JC9Ve1sfI

Tento program bude do nekonečna inkrementovat hodnotu v akumulátoru a ukládat ji na adresu 6.

Pozor! Ve skutečnosti (při práci s JSA (jazykem symbolických adres)) nejsou adresy číslovány v desítkové soustavě, ale v hexadecimální.

Proudové zpracování instrukcí (Pipelining)

Pipelining je způsob zvýšení výkonu procesoru současným prováděním různých částí několika strojových instrukcí. Základní myšlenkou je rozdělení zpracování jedné instrukce mezi různé části procesoru a tím i umožnění zpracovávat více instrukcí najednou (umožnění paralelizace na úrovni instrukcí). Počátek této technologie byl úspěšný zejména u procesorů s RISC architekturou, kde je díky jednoduchému setu instrukcí a především stejné délce všech instrukcí jednodušší implementace. Nicméně dnes se proudové zpracování nachází již téměř ve všech procesorech.

Je toho docíleno tím, že se snažíme udržet každou část procesoru zaneprázdněnou nějakou instrukcí. Každá instrukce je při proudovém zpracování rozdělena do sekvenčních kroků.

Při jednom tiknutí se tedy tedy instrukce může dekódovat, ale zároveň se již může natahovat / fetchovat další.


obr. 6: Postup proudového zpracování instrukcí
Dostupné z: https://en.wikipedia.org/wiki/Instruction_pipelining

O řízení proudového zpracování instrukcí se stará plánovač, který říká jednotlivým jádrům procesoru, na čem mají dělat. Často se také využívají buffery, do kterých se ukládají mezivýsledky jednotlivých fází proudového zpracování.

Ač se tato technologie dnes používá téměř ve všech procesorech, nese si i jisté nevýhody, zde jsou tři nejpodstatnější.

nutnost větších zdrojů: každá fáze zpracování musí být vykonávána samostatně - to vede k nutnosti více obvodů, procesorových jednotek, paměti pro buffery...
zvýšení latence: v některých případech nemůže procesor zpracovat část instrukce, dokud není plně zpracovaná předchozí část nebo se vyskytnou jiné potíže s režií proudového zpracování
zahození dat při přepnutí programu: data a instrukce, které se v pipelině právě nacházejí, musejí být zahozeny, aby se mohly začít vykonávat nové, jež nemají s předchozími nic společného (toto "uklizení" vede k větší režii)

Zdroje

The Fetch-Execute Cycle: What's Your Computer Actually Doing? [online] @2019 [cit. 15. 12. 2022] Tom Scott.
Dostupné z: https://www.youtube.com/watch?v=Z5JC9Ve1sfI
Instruction pipelining [online] @2023 [cit. 11.05.2023] Wikipedia: The Free encyclopedia.
Dostupné z: https://en.wikipedia.org/wiki/Instruction_pipelining

Soubor instrukcí

Soubor instrukcí: typy a kódování instrukcí, adresní módy. Zásobník procesoru. Rozdíly v souborech instrukcí v architekturách CISC a RISC.

Než začneme rozebírat soubory instrukcí, je třeba si říci, co je to instrukce.

Instrukce

Instrukce je kódový příkaz pro provedení elementární operace procesoru. Posloupnost instrukcí se nazývá strojový kód.

Některé procesory podporují více sad instrukcí (např. současné procesory pro počítače IBM PC kompatibilní podporují sadu x86-16, IA-32 a x86-64, které se celkově označují jako x86).

Zápis instrukce

Instrukce se skládá ze dvou částí:

operace
operandů

Operace označuje, co konkrétní instrukce dělá. Například operace SUB může být operace pro odečtení dvou čísel, JUMP může být operace pro přesun do jiné částí programu apod.

Operand určuje, s čím tato instrukce operaci dělá. Typicky se jedná o adresový prostor registrů a operační paměti.

Velikost instrukce

Velikost instrukce odpovídá počtu bitů dané architektury. Moderní procesory mají obvykle 64 bitů. Tzn. signál, který pokud by všude byly nuly tak vypadá takto:

0000000000000000000000000000000000000000000000000000000000000000

Druhy instrukcí

Instrukce dělíme podle svého určení

Přesunové instrukce
- Instrukce, jež se používají pro přesun dat mezi registry, pamětí a I/O. Instrukce i data jsou uloženy v paměti a procesor potřebuje číst instrukce a data z paměti a po zpracování je opět do paměti uložit.
  - Load (fetch) instrukce
  - Store (Write) instrukce
Aritmeticko-logické instrukce
- Nazývají se také instrukce pro manipulaci dat. Mohou to být aritmetické operace, logické operace nebo posuny.
  - Aritmetické operace : Sčítání, odčítání, sčítání s přenosem, násobení.....
  - Logické operace: AND, OR, XOR...
  - Posuny: Umožňují bitové posuny a rotace. Při přetečení nastavují carry bit.
Sekvenční / Řídící instrukce
- Tyto instrukce řídí tok programu tím, že mění program counter. Díky tomu může procesor vykonat instrukci na jiné adrese, než je ta sekvenčně následující. (Skočí na jiný řádek strojového kódu, než je ten následující).
Vstupně / výstupní instrukce
- Používají se pro přesun dat mezi pamětí / registry a vstupně / výstupními zařízeními.

Adresa operandu (Adresní módy)

Přímé adresování: Adresa může být určena buď přímo (tzv. přímé adresování) – jako konstanta určující index buňky v operační paměti počítače.
Nepřímé adresování: Druhou základní možností je nepřímé adresování, kdy je operandem registr jehož obsah je interpretován jako index buňky v operační paměti počítače. Je také možné schovat tento registr za ukazatel.
Okamžité adresování: Namísto, abychom se odkazovali na registr či adresu, používáme konstantní hodnotu.
Indexové adresování: Adresa operandu je vygenerována pomocí přidání konstantní hodnoty k obsahu registru. Tento registr může být speciální registr pro tento účel, nebo jeden z registrů procesoru. Tato generace se děje poté, co přistoupíme k operandu skrze předchozí adresu.
Relativní adresování: Podobný indexovému registrování, akorát namísto používání hodnoty registru ke generování adresy se využije program counter
Adresování s inkrementací / dekrementací: Po tom, co za pomocí instrukce přistoupíme k operandu skrze adresu v registru, je adresa tohoto registru inkrementovaná / dekrementována o 1.

Příklady instrukcí

add r0, r2; – sčítání – přičte do registru r0 hodnotu uloženou v registru r2
addc r0, r1; – sčítání s přenosem – přičte do registru r0 hodnotu registru r1 a příznaku přenosu (carry bit)
mov 1234h, r0; – přesun – uloží do paměti na adresu 1234h (přímé adresování) hodnotu z registru r0 (nepřímé adresování)
mov r0, 10; – přesun – uloží do registru r0 hodnotu 10 (okamžité adresování)
add 8(r0),r2; - sčítání - uloží do registru r0 hodnotu v registru r2 a poté přičte k adrese v registru r0 8 bitů. (indexové adresování)

Zásobník procesoru (Stack)

Jedná se o strukturu pro uložení dat. Jednotlivé hodnoty jsou v něm ukládaná způsobem LIFO (Last in, First out).

K zásobníku se váže speciální registr -> stack pointer. Tento registr obsahuje adresu prvku,který se přidal na zásobník jako poslední. Říká nám tedy, jak je zásobník velký.

Nejčastěji je zásobník část paměti počítače s pevně danou počáteční adresou a proměnnou velikostí.

Využití zásobníku je může být pro několik věcí :

Ukládání návratových adres a příznaky stavu procesoru při přerušeních. Po návratu je ze zásobníku získána návratová adresa a zpracování pokračuje.
Odkládání dat programátorem (například kopie registrů)
Některé instrukce používají zásobník pro uložení a obnovení adres (CALL a RET)

Tak nebo tak se jedná o odkládání a znovuzískávání dat.

Základní instrukce, jež se váží k zásobníku

Přesné znění těchto instrukcí se může lišit podle architekturu procesoru, ale jejich význam zůstává stejný.

PUSH r0 - vloží hodnotu v registru r0 na konec zásobníku
POP r1 - načte hodnotu na vrcholu zásobníku a uloží ji do registru r1. Na tuto adresu ukazuje stack pointer. Hodnota stack pointeru je poté změněna o velikost paměti kterou na zásobníku zabírala "popnutá" data.

Přetečení zásobníku

Pokud se stane, že stack pointer bude ukazovat na adresu vyšší, než je maximální povolená velikost zásobníku, dojde k přetečení. Pokud naopak bude ukazovat na adresu nižší, než je počáteční adresa zásobníku dojde k podtečení. Obojího lze docílit pomocí opakovaného používání instrukce PUSH a POP.

Hardwarová implementace

Většina CPU má zásobník implementovaný v hlavní paměti, některé počítače mohou mít zásobník implementovaný jako sérii registrů nebo jako hardwarově oddělenou paměť (speciální paměť, určena pouze pro zásobník).

Soubor instrukcí / Instrukční sada / ISA

Soubor instrukcí aneb Instrukční sada je abstraktní soubor pravidel, který jednoznačně definuje rozsah funkcionality procesoru = co může procesor dělat a jak to bude dělat.

Definuje tedy:

jednotlivé strojové instrukce
datové typy
registry
podporu hardware pro správu paměti
zvládání vyjimek a přerušení
klíčové vlastnosti (konzistenci paměti, adresní módy, virtuální paměť)
vstupně/výstupní model rodiny implementací ISA.

Tyto vlastnosti mají přímý vliv na výslednou implementaci procesoru. Pro programátora, resp. kompilátor, se pak jedná o dostupné prostředky procesoru implementujícího danou ISA (Instruction Set Architecture).

Implementace ISA

Zařízení (CPU), které provádí instrukce definované v určité ISA se nazývá implementace. ISA definuje pouze chování strojového kódu, který běží na implementaci této ISA, nezávisle na charakteristice této implementace. Toto poskytuje tzv. binární kompatibilitu mezi implementacemi. Binární kompatibilita umožňuje různé implementace totožné ISA, i když se tyto implementace liší v charakteristice (charakteristikami je myšlena například rychlost procesoru nebo fyzická velikost).

Mikroarchitektura

Mikroarchitektura zahrnuje implementaci základních operací, které jsou podporované počítačem a definované v ISA. Můžeme říct, že AMD Athlon a Intel Core 2 Duo jsou procesory, které jsou založení na stejné ISA ale mají každý jinou mikroarchitekturu s různým výkonem a efektivitou.

Typy ISA

Obecně rozlišujeme dva typy instrukčních sad. Když se vytvoří nová instrukční sada, povětšinou (pokud není hodně specifická) ji lze zařadit do dvou tříd.

RISC (Reduced Instruction set Computer, Redukovaná sada instrukcí)
CISC (Complex Instruction set Computer, Komplexní sada instrukcí)

Redukovaná sada instrukcí (RISC)

RISC je architektura, využívající jednoduché instrukce. Tyto instrukce mohou být procesorem vykonávány rychleji bez potřeby používat paměť tak často. RISC si klade za cíl redukovat exekuční čas pomocí zjednodušení instrukční sady. Díky tomu, že všechny instrukce mají stejnou délku, je možné je řetězit, což zefektivňuje jejich vykonávání (pipelining).

Charakteristiky RISC:

Relativně málo instrukcí
Relativně málo adresních módů
Přístup do paměti limitován na načítací a ukládací instrukce
Všechny operace se vykonávají pouze pomocí registrů CPU
Každá instrukce se vykoná v jednom instrukčním cyklu
Instrukce mají pevnou délku
Jednotlivé instrukce jso napevno dány sadou tranzistorů, nežli za pomocí mikro-programu.

Komplexní sada instrukcí (CISC)

CISC je architektura, kde jedna instrukce může provádět více operací. Například jediná instrukce může načíst z paměti a uložit do paměti. CISC tím minimalizuje počet instrukcí na program za cenu zvýšení cyklů na instrukci (instrukce se vykonává déle).

Charakteristiky CISC

Velký počet instrukcí (klasicky 100 - 250 instrukcí)
Některé instrukce, hlavně ty, které provádějí velmi specifické úkony, nejsou využívány často
Velké množství adresních módů (5 - 20)
Jedna "složitá" instrukce se může skládat z více "základních" instrukcí, tato instrukce zabere více cyklů na vykonání
Mikroprogramy určují vykonávání "složitých" instrukcí
Formáty instrukcí mají proměnnou délku
Instrukce, které manipulují s operandy v paměti

Příklad

Při provádění ADD operace, CISC provede jeden ADD příkaz, který vykoná jednotlivé potřebné kroky pro načtení a uložení zpět do paměti.

RISC provede každou operaci pro načítání dat z paměti, sečtení hodnot a zpětné uložení hodnoty do paměti pomocí jednotlivých low-level instrukcí.

Zásobník (datová struktura). Wikipedie : Otevřená Encyklopedie. [online] @2023 [citováno: 14.05.2023]
Dostupné z: https://cs.wikipedia.org/wiki/Z%C3%A1sobn%C3%ADk_(datov%C3%A1_struktura)
Lekce 1 - Assembler - Zásobník. itnetwork.cz. [online] @2023 [citováno: 14.05.2023]
Dostupné z: https://www.itnetwork.cz/assembler/os/assembler-zasobnik

Vstupně/výstupní operace

Vstupně/výstupní operace, vyvolání a obsluha přerušení, přímý přístup do paměti. Registry periferií, mapování periferií do paměti a do vstupně výstupního prostoru

Úvod

Jedná se o přenos dat mezi periferním zařízením či vnější pamětí a počítačem. Směr přenosu je definován z hlediska počítače, takže vstupní operace je čtení z periferie, zatímco výstupní operací je zaslání dat do periferie.

Periferní zařízení dělíme na 3 typy:

Vstupní: zařízení pouze zasílá data do počítače, například senzor
Výstupní: zařízení pouze přijímá data od počítače, například monitor
Vstupně/Výstupní: zařízení jak přijímá, tak zasílá data. Například síťová karta nebo externí disk

Přenos dat probíhá skrze vstupně-výstupní rozhraní (I/O interface), klasicky řečeno port.

Každé vstupně-výstupní rozhraní má svoji adresu, které se říká Vstupně/výstupní port. K této adrese je přiřazen hardwarový registr vstupně-výstupního rozhraní nebo samotné zařízení, které je na toto rozhraní připojené -> adresa buď odkazuje na hardwarový registr, nebo na samotné zařízení.

Počítač může mít tuto adresu uloženou na dvou různých místech

v adresním prostoru paměti
- procesor s nimi může pracovat jako s klasickou pamětí
- mluvíme pak o adresově mapovaných portech
- adresy, které se zde nacházejí se sem dostali pomocí mapování periferií do paměti
v odděleném adresním prostoru
- jsou procesoru přístupné pomocí speciálních instrukcí IN a OUT
- mluvíme pak o izolovaných portech
- adresy, které se zde nacházejí se sem dostali pomocí mapování periferií do vstupně výstupního prostoru

Periferní zařízení se vždy připojuje k hardwarovému rozhraní. Součástí tohoto rozhraní je několik hardwarových registrů, jejichž adresy má počítač uložené v jednom ze dvou prostorů zmíněných výše. Hardwarové registry se také nazývají registry periferií.

Procesor komunikuje se vstupně/výstupními zařízeními pomocí hardwarových registrů jež jsou dostupné pomocí sběrnice daného rozhraní.

Výstupní hardwarové registry

Vstupní zařízení mají navíc výstupní hardwarové registry, pro synchronizaci, časování apod. Registry mohou mít velikost 1B a mohou sloužit jako vyrovnávací paměť daného HW (hardware cache), neboť v sobě udrží data do doby. než jsou předána CPU, RAM či naopak zpracována samotnou periferií.

Ovladače

Jednotlivá hardwarová rozhraní jsou ovládány pomocí ovladačů (například Realtek Audio pro zvukový výstup).

ovladače pro hardwarové rozhraní lze nalézt na stránce výrobce základové desky

Stejně tak mají periferní zařízení vlastní ovladače dodávané výrobci.

Nabouchaná myš od Logitechu potřebuje speciální software, aby mohla svítit jak vánoční stromeček.

Ovladač je software, který umožňuje počítači komunikovat s periferií, nebo naopak periferii komunikovat s počítačem.

Připojení zařízení ke sběrnici - mapování periferií do paměti a do I/O prostoru

Pokud připojíme zařízení ke sběrnici skrze vstupně/výstupní rozhraní tak je adresa hardwarových registrů uložena do jednoho ze dvou paměťových prostorů. Tomuto procesu říkáme mapování periferie.

Výběr prostoru je dán typem periferie, která při připojení vyšle na jeden z hardwarových registrů rozhraní, na které je připojena, signál, určující, kam bude namapována. O mapování periferie, stejně jako o správu komunikace, se starají ovladače periferií. Již jsme si tyto dva prostory zmínili výše. Periferii (její hardwarové registry) můžeme namapovat do:

paměti RAM
vstupně / výstupního prostoru

Mapování periferie do paměti

Adresa periferie je uložena do operační paměti.

Procesor může k této adrese přistupovat stejně, jako k ostatním adresám, tj. pomocí klasické sady instrukcí. Může tedy používat klasické adresná módy a číst / zapisovat do registru klasickým způsobem
Je vhodnější (jednodušší) pro programování
Procesor se chová k periferiím namapovaným zde jako k adresám
Adresní prostor je velký
Přístup zde je pomalejší (je potřeba dekódovat adresu, což trvá dlouho kvůli velkému adresnímu prostoru)

Mapování periferie do vstupně/výstupního prostoru

Adresa periferie je uložena do speciálního adresního prostoru.

Prostor oddělený od operační paměti. Tento adresní prostor má vlastní sběrnici, která je připojena k CPU
Adresní prostor je malý
Přístup je zde rychlejší, nežli do paměti (malý adresní prostor = jednodušší dekódování)

Dekodér adres

Jedná se o integrální součást řadiče. Používá se pro dekódování adres. Pokud chceme přistoupit k nějakému místu v paměti, tak procesor vystaví na sběrnici adresu. Prací řadiče je vybrat správnou paměťovou buňku v paměti, ke které přistupujeme, převést adresu ze sběrnice na místo v paměti (toto právě řeší adresový dekodér), které je symbolizováno danou adresou. De facto řadič sáhne do správné paměťové buňky (dle adresy vystavené procesorem a dekodérem převedené na adresu paměťové buňky) a vytáhne z ní data, o něž si CPU řekl.

ŘÍzení komunikace - přerušení a přímý přístup do paměti

Periferie a CPU spolu potřebují komunikovat. Mohou nám nastat dvě různé situace:

procesor chce komunikovat s periferií (chce ji zaslat data)
periferie chce komunikovat s procesorem (chce mu zaslat data)

V prvním případě jednoduše procesor zašle data na danou adresu, která odpovídá adrese hardwarového registru periferie.

V druhém případě je to složitější, periferie si může přát zaslat data, ale procesor může být zaneprázdněný a nemá žádný způsob, kterým by mohl vědět, že periferie chce komunikovat.

Periferní zařízení může komunikaci uskutečnit dvěma způsoby :

přerušení
přímý přístup do paměti (DMA)

Přerušení

Princip přerušení spočívá v tom, že periferie vystaví signální bit, kterým si zažádá o čas procesoru. Pokud je procesor volný, tak periferii obslouží na základě toho, jaké signály jsou periferií vystaveny (těmto signálům se říká signal word).

Pokud procesor volný není, tak periferie musí čekat, až bude obsloužena. Povětšinou není jediná, která vystavila signál k přerušení. O tom, jaké přerušení bude obslouženo nejdříve, rozhoduje řadič přerušení.

Přímý přístup do paměti

Ne vždy je nutné vyžadovat po CPU čas pro vykonání operace. Příkladem může být přesun velkého bloku dat z a nebo do paměti. V případě přímého přístupu do paměti je toto uskutečněno bez asistence procesoru.

Zdroje

Vstup/výstup. Wikipedie: Otevřená Encyklopedie. [online] @2022 [citováno 19.05.2023]
Dostupné z: https://cs.wikipedia.org/wiki/Vstup/v%C3%BDstup
Komunikace s perifériemi. Ing. Petr Olivka. [online] @2010 [citováno 19.05.2023]
Dostupné z: https://poli.cs.vsb.cz/edu/arp/down/komunikace.pdf
Memory-mapped I/O and port-mapped. Wikipedia : The Free Encyclopedia. [online] @2023 [citováno 19.05.2023]
Dostupné z: https://en.wikipedia.org/wiki/Memory-mapped_I/O_and_port-mapped_I/O

Paměťový podsystém počítače

Typy pamětí a jejich hierarchie. Skrytá paměť (cache), princip činnosti, konstrukce a vliv na rychlost výpočtu. Virtuální adresní prostor, překlad virtuální adresy na fyzickou metodou stránkování. TLB (Translation lookaside buffer).

Typy pamětí

Registry

Registry jsou tou nejdůležitější pamětí počítače. Nacházejí se uvnitř procesoru, který je využívá při prakticky veškeré své činnosti. Jsou nejrychlejší, ale zároveň nejmenší pamětí v počítači. Máme dva základní druhy registrů:

obecné
- slouží k ukládání operandů a výsledků operací procesoru (tedy dat) nebo paměťových adres (někdy jsou datová a adresní registry odděleny, jindy se pro obojí používá jedna sada)
- můžeme s nimi programově pracovat
- jsou jich obvykle desítky a mají velikost jednoho slova (odpovídá počtu bitů architektury), ale většinou lze přistupovat i k jejich částem (např. pro 64 b jen k 32 nebo 16 b)
- první z nich (RAX) měl historicky speciální postavení, nazýval se akumulátor a používal se k ukládání výsledků aritmetických operací (bal tedy vytížen mnohem více než ostatní)
speciální
- mají konkrétní účel a jejich hodnotu obvykle nemůžeme sami v programu měnit, pouze ji číst
- Instrukční registr (IR)
  - drží instrukci, která bude provedena v rámci instrukčního cyklu
  - v programu nepřístupný
- Program Counter (PC)
  - drží adresu instrukce právě načtené v IR
  - mění se obvykle o délku právě vykonané instrukce
  - můžeme jej měnit pomocí skokových instrukcí (JUMP)
- Program Status Word (PSW)
  - udržuje stavové informace a příznaky (flags) procesoru
  - někdy též nazýván FLAGS
  - nejběžnější příznaky:
    - Z (zero) - výsledek operace je nulový
    - C (carry) - výsledek aritmetické operace způsobil přetečení z nejvyššího řádu, často se užívá také v posuvech
    - V (overflow) - výsledek aritmetické operace v doplňkovém kódu je mimo rozsah (např. v osmibitovém registru 127 + 1 nebo -127 - 2).
    - N (negative) - výsledek je záporný
    - I (interrupt) - příznak povolení přerušení (1 povoleno, 0 - zakázáno); nastavuje se programově
  - Stack pointer (SP)
    - udržuje adresu vrcholu zásobníku (tedy jeho elementu, se kterým se bude pracovat příště)


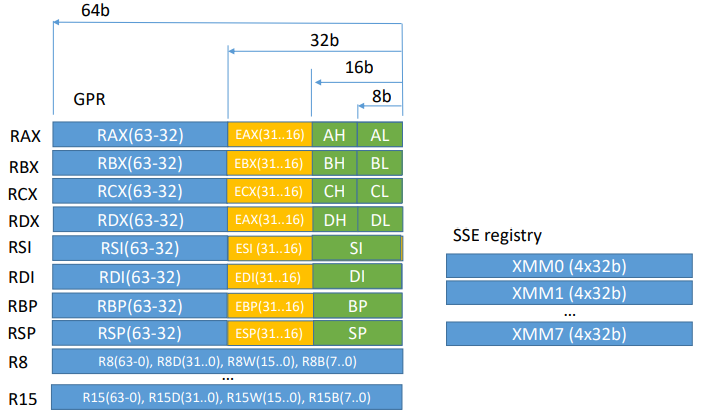obr. 1: Hlavní část registrů pro architekturu AMD64 (SSE registry slouží pro SIMD operace nad daty v plovoucí řádové čárce)
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Cache

Paměť typu cache je vzhledem ke struktuře otázky popsána níže.

Hlavní paměť

Hlavní, nebo též operační paměť slouží k ukládání jak instrukcí, tak dat spuštěných úloh, stejně jako samotného operačního systému. Nejedná se o trvalé ukládání, drží se pouze po dobu činnosti počítače (když je zapnutý). Jde o paměť typu RAM (Random Access Memory), což znamená, že v kteroukoliv chvíli lze přistoupit k jakékoliv její části.

Hlavní paměť je adresována nejčastěji po bytech (může být i povětších sekcích). K vývěru paměťové buňky, na kterou chceme přistoupit slouží adresová sběrnice. Ta má velikost odpovídající počtu bitů dané architektury (např. 64 b). Tím je také omezena maximální velikost paměti, protože můžeme adresovat maximálně $ 2^n $ paměťových buněk, kde $ n $ je počet bitů sběrnice.

Operační systém řídí to, jakým způsobem se s pamětí nakládá, jak se přiděluje a uvolňuje, atd. Ve většině systémů mu k tomu slouží MMU (Memory Management Unit). Principy nakládání s pamětí jsou blíže popsány v otázkách 2.3.2 a 2.3.3.


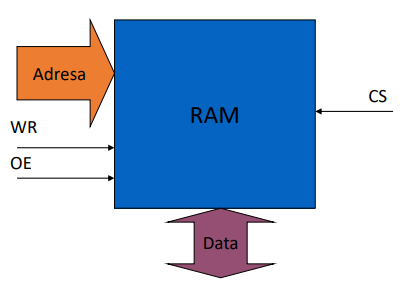obr. 2: Základní činnost hlavní paměti
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Význam jednotlivých vstupů na obrázku je následující:

CS (Chip Select) - říká RAM, že bude docházet ke čtení nebo zápisu (startuje činnost); řadič začne číst adresu
WR - indikuje zápis (data ze sběrnice se začnou zapisovat na pozici adresy)
OE - indikuje čtení (data z adresy se zapíší na sběrnici)

Máme dva základní druhy RAM:

statická (SRAM)
- paměťové buňky jsou realizovány jako BKO (bistabilní klopný obvod) typu CMOS
- cache je často tvořena SRAM
- má skvělé vlastnosti:
  - nízkou spotřebu
  - minimální přístupovou dobu
  - vysokou odolnost proti šumu
- je však velmi drahá, a proto se vyplatí pouze pro malé paměti (max desítky MB)
dynamická (DRAM)
- buňky jsou realizovány parazitními kapacitami (funkčně ekvivalent kondenzátoru)
- jsou mnohem levnější a jednodušší na výrobu
- mají však výrazně horší všechny vlastnosti
- velkou nevýhodou je nutnost periodicky obnovovat náboj buněk (říká se tomu refresh)
- v klasických počítačích se používají jako hlavní paměť takřka výhradně
- typů DRAM existovala historicky celá řada:
  - SIMM
  - DIMM
    - SDR (SDRAM)
    - DDR
      - DDR1...5
  - SO-DIM
  - RIMM (RDRAM)

Čtení z hlavní paměti

na adresní sběrnici se vystaví adresa
započne čtecí cyklus (vyšle se čtecí signál)
na datovou sběrnici se vystaví data
ukončí se čtecí cyklus (čtecí signál se vrátí do neaktivní hodnoty)

Pro urychlení čtení se hlavní paměť (pouze u DDR) dělí na tzv. banky, které mohou pracovat nezávisle, tedy je možno z nich číst paralelně. Jejich rozhraní (adresová a datová sběrnice, atd.) jsou však společné, požadavky je tedy nutno zadávat postupně. Zadávání je ale mnohem rychlejší, než samotné čtení, díky čemuž tato metoda i tak přináší výrazné zrychlení.

Zápis do hlavní paměti

na adresní sběrnici se vystaví adresa
na datovou sběrnici se vystaví data
započne zápisový cyklus (vyšle se zápisový signál)
ukončí se zápisový cyklus (zápisový signál se vrátí do neaktivní hodnoty)


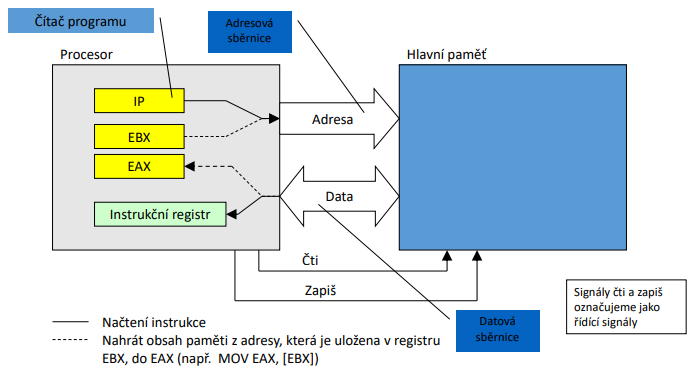obr. 3: Přenos dat mezi CPU a hlavní pamětí
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Sekundární paměť

Slouží k trvalému ukládání dat (je nevolatilní), tedy i po vypnutí počítače. Může být:

interní - přímo součást PC; je zde uložen OS a data uživatelů
externí - připojuje se podle potřeby; často se užívá pro přenos mezi zařízeními

Jako interní se obvykle používají:

HDD (Hard Disk Drive)
- mechanická komponenta
- pomalejší (neexistuje zde přímý přístup, plotny se musí správně natočit a hlava nastavit)
- zatím stále nižší cena na jednotku paměti (oproti SSD), ale postupně se vyrovnávají
- HDD má následující součásti:
  - hlavy - čtecí zařízení
  - plotny (desky) - kovové disky, na které se zmagnetizováním konkrétních míst ukládají data
  - stopy - soustředné kružnice na plotnách
  - sektory
    - výseče kruhu (jednotlivé paměťové bloky)
    - čím dále od středu, tím více sektorů ve stopě
  - cylindry - množina stop nad sebou
SSD (Solid State Drive)
- polovodičová paměť (NAND flash)
- přístup k paměti je přímý
- mnohem rychlejší než HDD
- data se po dlouhé době bez napájení začínají ztrácet
- počet zápisů je omezen (avšak často odejde řídicí elektronika dříve než podstatná část paměťových buněk)


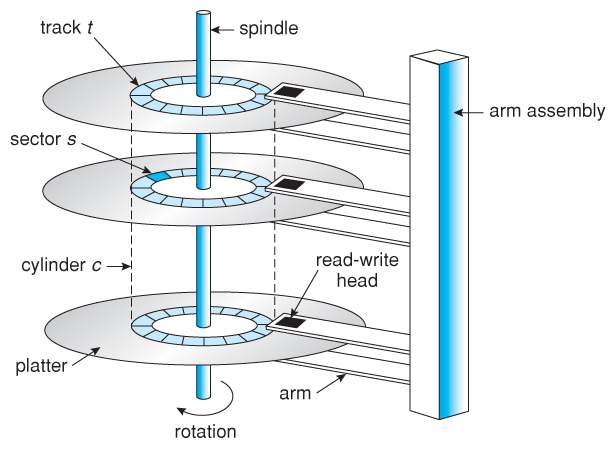obr. 4: Vnitřní struktura HDD
zdroj: https://www.cs.uic.edu/~jbell/CourseNotes/OperatingSystems/10_MassStorage.html

Externí paměti jsou obvykle variacemi ROM (Read Only Memory). Dnešní typy ROM už obvykle umožňují i zápis, ale stále je zde omezení počtu přepisů. Běžné druhy jsou:

ROM - obsah je "vypálen" od výrobce (např. jednoúčelové čipy, předzapsané CD-ROM, ...)
PROM (Programable ROM) - obsah může zapsat uživatel, ale pouze jednou (CD-ROM, DVD-ROM, ...)
EPROM (Erasable PROM)
- obsah lze i smazat (nejčastěji pomocí UV světla do speciálního okénka)
- velmi nízký počet přepisů
- už se nepoužívají
EEPROM (Electrically EPROM)
- lze vymazat elektricky
- většinou stovky až tisíce přepisů
- např. pro uchování hodnot po vypnutí mikrokontroléru
Flash
- vysoká kapacita a rychlost RW
- stovky tisíc přepisů

Hierarchie pamětí

Hierarchie paměti počítače je z pohledu rychlosti (od nejrychlejší) a celkově postupu činnosti následující:

registry
skrytá paměť
hlavní paměť
sekundární paměť


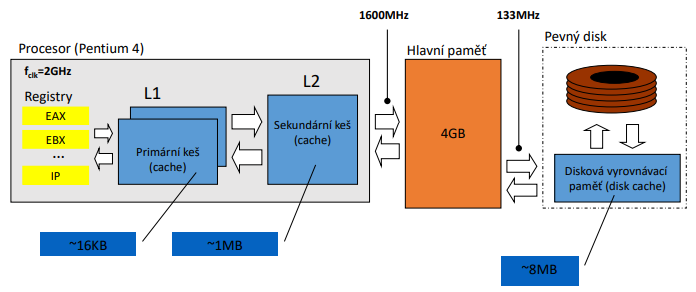obr. 5: Hierarchie paměti (zleva doprava)
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Skrytá paměť (cache)

Druhým nejrychlejším typem paměti je tzv. skrytá paměť, neboli cache. Jejím primárním účelem je vyrovnávat rozdíly mezi rychlostí přístupu k registrům v procesoru (a obecně rychlosti jeho činnosti) a rychlostí přístupu k hlavní paměti počítače (která je mnohonásobně pomalejší). Z pohledu velikosti leží cache, stejně jako u rychlosti, mezi registry a hlavní pamětí. Cache je navržena tak, aby procesor nepoznal, jestli komunikuje s ní, nebo s hlavní pamětí, je tedy transparentní.

Z funkčního hlediska lze činnost cache shrnout tak, že při prvním přístupu k datům musím procesor čekat na hlavní paměť, avšak při dalších přístupech je bržděn mnohem méně (protože už přistupuje pouze do cache).

Cache bývá obvykle třístupňová (L1, L2, L3), díky tomu je vyrovnávání pozvolnější. Platí, že čím blíž je stupeň k procesoru, tím je rychlejší, ale má menší kapacitu.

Vrstva	Velikost	Rychlost
L1	~ 16 kB	podobná rychlosti činnosti procesoru
L2	~ 1 MB	pomalejší
L3	~ jednotky až desítky MB	ještě pomalejší

Princip činnosti

Procesor potřebuje získat data z hlavní paměti, zadá tedy požadavek. Ten však nejde přímo do hlavní paměti, ale nejprve do cache (L1). Tam dojde ke zjištění, zdali tato data obsahuje. Pokud ano, nazývá se to cache HIT, data jsou přečtena z cache a požadavek je dokončen. Pokud data neobsahuje, nazýváme to cache MISS, pokračuje požadavek k dalším vrstvám cache a pokud ani tam není úspěšný, dojde až do hlavní paměti a data jsou vyčtena odtamtud. V tomto případě také dochází k zápisu vyčtených dat do cache, pro urychlení příštího čtení.


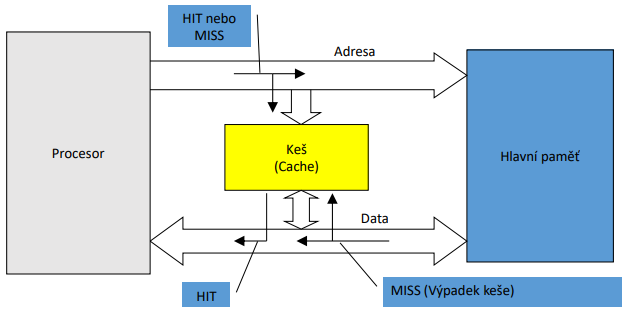obr. 6: Princip činnosti cache
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.

Z popisu výše je patrné, že je důležité, aby cache obsahovala především ty části paměti, které jsou častou využívány. To je potřeba řešit při odebírání položek (ke kterému dochází při přidávání nových) a máme k tomu různé postupy:

náhodný výběr - náhodně se zvolí položka z řádku, do kterého zapisujeme
FIFO - odebírá se nejstarší položka
LFU (Least Frequently Used) - každá položka má svůj čítač; vždy když se položka použije, ostatní čítače se inkrementují (odstraňuje se nejvyšší)

Konstrukce a vliv na rychlost výpočtu

Cache paměti mohou být konstruovány třemi základními způsoby (podle jejich asociativnosti):

plně asociativní
- v tomto případě mohou být paměťové bloky (z hlavní paměti) uloženy kdekoliv (v kterémkoliv řádku) v cache
- toto je nejjednodušší na provedení, ale následné hledání požadovaného bloku je extrémně náročné (musí se projít celá paměť, řádek po řádku)
přímo adresovaná
- má stupeň asociativity = 1
- toto je opačný způsob, zde má každý blok přesně dané jedno místo (jeden řádek), kam může být uložen
- zde je naopak prohledávání velmi jednoduché, ale nelze zde optimálně odstraňovat nepoužívané bloky (vždy musíme odstraňovat z toho jednoho řádku, ka zrovna zapisujeme)
s omezenou asociativitou
- stupeň asociativity > 1
- kompromis mezi předešlými metodami
- zde máme cache rozdělenou na segmenty, z nichž každý obsahuje $ n $ řádků ($ n $ se nazývá stupeň asociativity)
- často se používají stupně asociativity 2 a 4

Adresa, pomocí které přistupujeme k paměťové buňce se skládá za tří částí:

tag - určuje segment, kde se buňka nachází
index - určuje řádek v segmentu
offset - určuje pozici v řádku

Virtuální adresní prostor

Je logický adresní prostor (není fyzický), který se do fyzického (skutečně instalovaná paměť v počítači) pouze mapuje. Děje se tak skrze soustavu tabulek.

virtuální adresní prostory mohou být např. přiřazené konkrétnímu procesu (pro ukládání dat jeho úlohy)
celková velikost všech VAP převyšuje velikost fyzické paměti
celková velikost aktuálně namapované VAP však musí být menší než je velikost fyzické paměti
mapa adresního prostoru
- popisuje obsazení adresního prostoru fyzickou pamětí
- bývá nesouvislá
- obsahuje různé paměti, které jsou k počítači připojeny (RAM i ROM)
- ja nutné ji znát při programování na úrovni OS
způsoby, jakými k mapování dochází, popisují detailně otázky 2.3.2 a 2.3.3.

Translation lookaside buffer

Translation lookaside buffer (TLB) je asociativní paměť (s částečnou nebo plnou asociativitou), která urychluje překlad adres z VAP na fyzický adresní prostor. Zrychlení spočívá v tom, že TLB v sobě uchovává páry virtuální adresa – fyzická adresa a v těchto párech vyhledává asociativně s klíčem virtuální adresa.

Zdroje

SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.
Přispěvatelé Wikipedie, Registr procesoru [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 23. 11. 2022, 09:50 UTC, [citováno 17. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Registr_procesoru&oldid=21929380
https://cvw.cac.cornell.edu/codeopt/cacheassociativity
https://en.algorithmica.org/hpc/cpu-cache/associativity/
Přispěvatelé Wikipedie, RAM [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 1. 05. 2023, 02:57 UTC, [citováno 19. 05. 2023] https://cs.wikipedia.org/w/index.php?title=RAM&oldid=22752301
PECH, Jiří. Operační systémy 1 - Struktura odkládacího zařízení. České Budějovice.

Flynnova klasifikace paralelních systémů

Flynnova klasifikace paralelních systémů (SIMD, MIMD, SISD, MISD), Amdahlův zákon, měření výkonnosti počítačů, benchmarky

Michael J. Flynn, narozen 20. května 1934 navrhl v roce 1996 tzv. Flynnovu Taxonomii, která nabízí kategorizaci pro strukturu počítače na základě toku instrukcí a toku dat. Tedy na počtu instrukcí a datových položek, které lze paralelně (najednou) zpracovat.

Tok instrukcí
- jedná se o sekvenci instrukcí čtenou z paměti (program)
Tok dat
- jedná se o operace prováděně na datech v procesoru

Můžeme paralelně zpracovávat tok instrukcí, tok dat, nebo obojí. Toto nám dává dohromady 4 kombinace, v závislosti na tom, zdali jsou toky sériové (jeden tok) nebo paralelní (více toků).

Rozdělení počítačů podle Flynnovy klasifikace

Single Instruction Stream, Single Data Stream (SISD)
Single Instruction Stream, Multiple Data Streams (SIMD)
Multiple Instruction Streams, Single Data Stream (MISD)
Multiple Instruction Streams, Multiple Data Streams (MIMD)

Single Instruction Stream, Single Data Stream (SISD)

Tato architektura reprezentuje tradiční výpočetní systém. Jeden program (tok instrukcí) se provádí na jednom setu dat (toku dat). Toto odpovídá programu napsanému pomocí procedurálního programovacího jazyka. Program běží na jedno-jádrovém CPU.


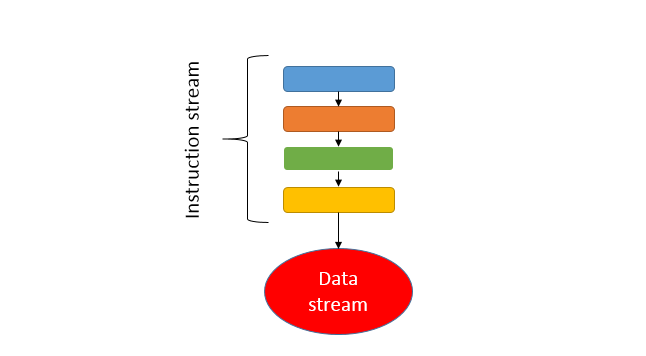obr. 1: Reprezentace SISD. Každá barva bloku odpovídá jiné instrukci.
Dostupné z: https://study.com/academy/lesson/flynns-architecture-taxonomy-types-alternatives.html

Single Instruction Stream, Multiple Data Streams (SIMD)

Jedna z nejčastějších paralelních architektur, díky její efektivitě. Je napsán jeden program, jehož kopie běží na různých CPU jádrech. V této architektuře musí být dosažena synchronizace na úrovni instrukcí. Jinak řečeno, v určitý moment by měla totožná instrukce běžet na všech procesorech a každý procesor vykoná tuto instrukci na datech, která má k dispozici.


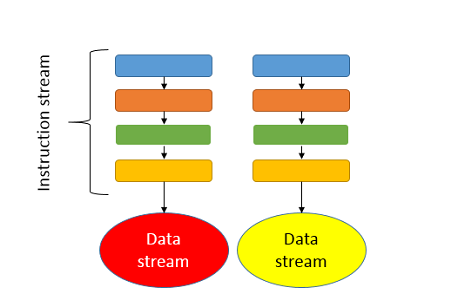obr. 2: Reprezentace SIMD. Každá barva bloku odpovídá jiné instrukci. Ve stejnou chvíli se vykonává na různých datech tatáž instrukce
Dostupné z: https://study.com/academy/lesson/flynns-architecture-taxonomy-types-alternatives.html

Multiple Instruction Streams, Single Data Stream (MISD)

Toto není příliš používaná architektura. Je používána pokud chceme aplikovat nebo testovat různé algoritmy na totožných datech. Například aplikace různých grafických filtrů na stejný obrázek.


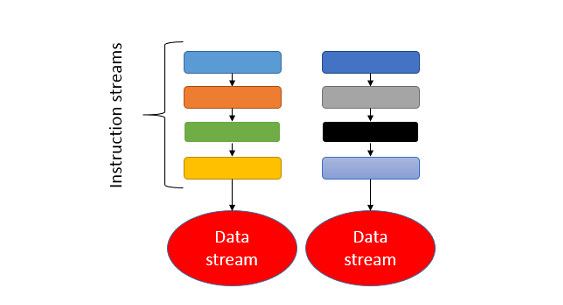obr. 3: Reprezentace MISD. Každá barva bloku odpovídá jiné instrukci. Ve stejnou chvíli se vykonává na stejných datech různá instrukce
Dostupné z: https://study.com/academy/lesson/flynns-architecture-taxonomy-types-alternatives.html

Multiple Instruction Streams, Multiple Data Streams (MIMD)

Toto je v dnešní době nejvíce využívaná architektura. Různé instrukce jsou vykonávány na různých datech. Dnes jsou všechny více-jádrové CPU považovány za MIMD, neboť každé CPU může vykonávat jiný tok instrukcí (program) na různých datech.


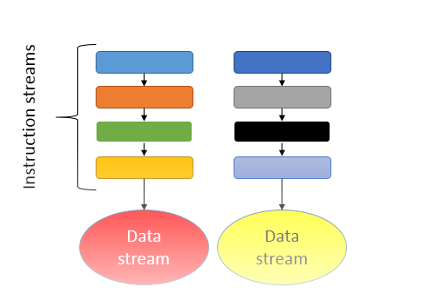obr. 4: Reprezentace MIMD. Každá barva bloku odpovídá jiné instrukci. Ve stejnou chvíli se vykonává na různých datech různá instrukce
Dostupné z: https://study.com/academy/lesson/flynns-architecture-taxonomy-types-alternatives.html

Amdahlův zákon

Jedná se o pravidlo, k vyjádření maximálního předpokládaného zlepšení systému poté, co je vylepšena pouze některá z jeho částí.

Využívá se např. u víceprocesorových systémů k předpovězení teoretického maximálního zrychlení při přidávání dalších procesorů.

Velikost zlepšení ze značí S a můžeme ji vypočítat následovně:


obr. 5: Výpočet maximálního zlepšení
Dostupné z: https://cs.wikipedia.org/wiki/Amdahlův_zákon

Pokud chceme zjistit maximální zlepšení celého systému při vylepšení pouze některých částí, postup je následovný:


obr. 6: Výpočet maximálního zlepšení při vylepšení některé z jeho částí
Dostupné z: https://cs.wikipedia.org/wiki/Amdahlův_zákon

Platí, že: Zvýšení výkonnosti dosažitelné nějakým zlepšením je omezené mírou používání tohoto zlepšení. Je zde tedy omezení, pokud budeme zlepšovat algoritmus, který tvoří 10% výpočtů programu. Největšího zlepšení dosáhneme, pokud budeme zlepšovat nejčastěji používané části.

Měření výkonnosti počítačů

Při měření výkonnosti musíme vzít v potaz dva hlavní parametry:

taktovací frekvence
počet taktů nutný na vykonání instrukce

Jen jeden parametr nám nestačí, protože nebudeme schopni porovnat různé architektury na různých programech.

Ale co když máme různé programy, každý s jinými instrukcemi. Pokud spočítáme rychlost výkonu na nějakém programu, tak tato hodnota nebude odpovídat skutečnému výkonu (například zpracování jiného programu).

Máme dva způsoby jak měřit výkonnost počítače:

Workload
- Jedná se o simulování typické zátěže počítače pomocí spouštění typických programů. Je to složité na automatizování (opakované a opakovatelné spouštění).
Benchmarky
- Jsou programy, které jsou specificky určeny k měření výkonnosti. Často se používají sady benchmarků, které testují různé aspekty a doufáme, že měření předpoví chování počítače při stejné zátěži.

Časem vznikl cíl, vytvořit sady benchmarků, které budou vhodné pro jednoduché porovnání výkonnosti. Tyto sady obsahují testy, které pokrývají běžné úkony procesoru pro co nejvíce optimální výsledek.

existují různé sady pro měření různých věcí (CPU, GPU, překladače, emaily, databázové vyhledávače, atd.)

Máme sady benchmarků, které měří výkonnost celočíselných výpočtů (překladač C, šachový algoritmus, simulace kvantového počítače, atd.) nebo i sady pro měření výkonnosti operací s plovoucí čárkou (metoda konečných prvků, molekulární dynamika, atd.).

Problémy při měření výkonnosti

Očekáváme, že při při zlepšení výkonnosti části systému dojde k úměrnému zlepšení výkonnosti celého systému.
- toto není pravda, viz Amdahlův zákon
Používáme špatná měřítka výkonnosti
- nemůžeme použít pouze jednu či dvě metriky (taktovací frekvence, počet instrukcí, atd.)
- existuje závislost mezi těmito metrikami (taktovací frekvence závisí na chlazení; počet taktů na vykonání instrukce závisí na konkrétní instrukci, atd.)

Zdroje

Flynn's Classifcation of Computers, [online] ©2022 [cit. 6.12.2022] Javapoint. Dostupné z: https://www.javatpoint.com/flynns-classification-of-computers
Flynn's Architecture Taxonomy: Types & Alternatives. [online] ©2022 [cit. 6.12.2022] Shadi Aljendi. Dostupné z: https://study.com/academy/lesson/flynns-architecture-taxonomy-types-alternatives.html
Amdahlův zákon, [online] ©2022 [cit. 6.12.2022] Wikipedie: Otevřená Encyklopedie. Dostupné z: https://cs.wikipedia.org/wiki/Amdahlův_zákon
Architektura počítačů: Výkonnost počítačů, [online] ©2019 [cit. 6.12.2022] Karlova Univerzita v Praze, fakulta matematiky a fyziky. Dostupné z: hhttps://d3s.mff.cuni.cz/legacy/teaching/computer_architecture/docs/02_vykonnost.pdf

Vícejádrové a vícevláknové procesory

Vícejádrové a vícevláknové procesory, architektura VLIW, procesory pro grafické karty (GPU)

Vícejádrové procesory

Jedná se o jeden procesor, který obsahuje více jader. Jednotlivá jádra mohou individuálně číst a vykonávat programová instrukce. -> Fyzicky vykonávají více instrukcí zároveň. Toto zrychluje vykonávání programu a podporuje paralelní zpracování.

Vícejádrové procesory jsou používány v aplikacích jako je síťování, embedded systémy, zpracování digitálního signálu a grafice (GPU).

Vícevláknové procesory

Jedná se o procesory, kde je jedno jádro schopné konkurentně zpracovávat více vláken.

Vlákno

Jedná se o sekvenci programových instrukcí. Vlákna, nebo spíše to, kdy se jaké vlákno vykonává (na určitém jádru), je řízeno plánovačem skrze přepínání kontextů.


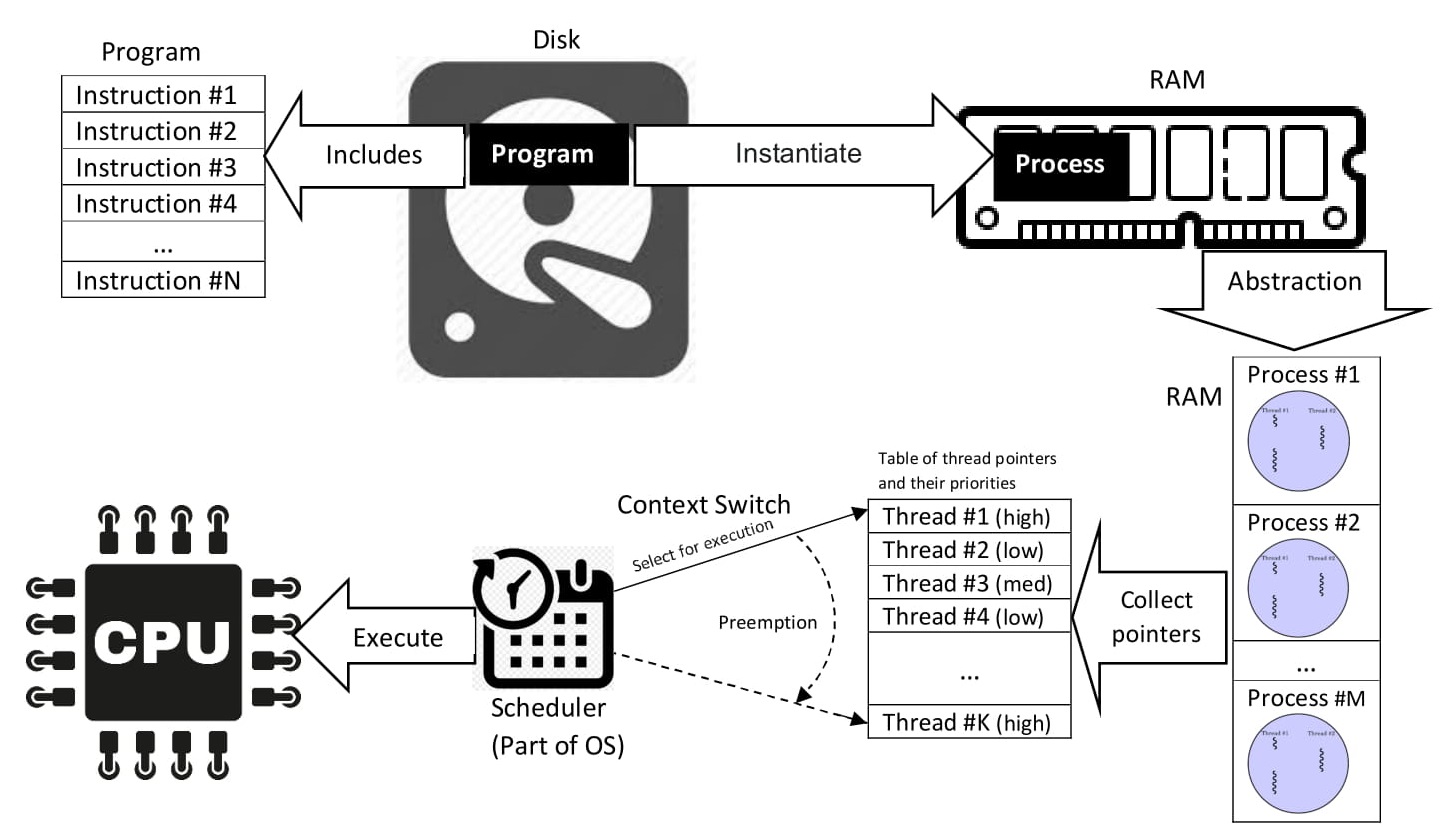obr. 1: Přeměna programu na vlákna Dostupné z: https://en.wikipedia.org/wiki/Thread_(computing)

VLIW (Very Long Instruction Word) architektura

Jedná se o architekturu, která si klade za cíl paralelismus na úrovni samotných instrukcí. Instrukce je zde rozdělena na samostatné bloky, tak aby se každá část instrukce vykonávala v jednom tiku procesoru. Tomuto říkáme proudové zpracování.

VLIW architektura, oproti klasickému proudovému zpracování přesouvá vnitřní složitosti ohledně proudového zpracování na kompilátor nebo vývojové prostředí. Vývojáří musejí instrukce předem naplánovat a zorganizovat je do jednoho tzv. slova, aby se mohli provádět paralelně. Toto slovo se skládá z jednotlivých nízkých instrukcí.

Výhodou tohoto přístupu oproti obyčejnému proudovému* zpracování je možnost použít jednodušší hardware, protože nám odpadá nutnost režie proudového zpracování.

Nicméně, nevýhody jsou ty, že architektury typu VLIW jsou jsou závislé na plánování instrukcí kompilátorem nebo vývojovým prostředím. Pokud tomu tak není, vznikají prodlevy, které vedou ke snížení výkonu.

Využití :

Všude tam. kde máme vysoký stupeň paralelismu a ve kterých lze instrukce dobře předem plánovat. Převážně zpracování digitálního signálu nebo multimediální aplikace.

Procesory pro grafické karty (GPU)

GPU byly původně vytvořeny pro vykreslování počítačové grafiky, ale časem se jejich využití rozšířilo i na zrychlení výpočtů, jež zahrnují velké množství dat.

GPU umožňuje provádění velkého množství repetitivních výpočtů paralelně s během hlavního programu na CPU. Na CPU se můžeme dívat jako na task mastera celého systému, který koordinuje velké množství obecných výpočetních úkonů. Pokud jsou nějaké úkony matematicky výpočetně náročné, jsou předány GPU.


obr. 2: Struktura CPU vs GPU Dostupné z: https://www.heavy.ai/technical-glossary/cpu-vs-gpu

Ač dokáže GPU zpracovávat data několikrát rychleji díky masivnímu využití paralelismu nežli CPU, tak GPU není tak všestranné. Je uzpůsobeno pouze na matematicky jednoduché výpočty, nejčastěji práci s maticemi.

Kromě renderování se GPU využívá take v:

strojové učení: (snížení doby trénování)
simulace

Zdroje

Multithreading (computer architecture). Wikipedia : The Free encyclopedia [online] @2023 [citováno: 18.05.2023]
Dostupné z: https://en.wikipedia.org/wiki/Multithreading_(computer_architecture)
Thread (computing). Wikipedia : The Free encyclopedia [online] @2023 [citováno: 18.05.2023]
Dostupné z: https://en.wikipedia.org/wiki/Thread_(computing)
CPU vs GPU. *HeavxAI [online] @2022 [citováno: 18.05.2023]
Dostupné z: https://www.heavy.ai/technical-glossary/cpu-vs-gpu

Linková vrstva

Linková vrstva MAC, ETHERNET (MAC adresa, rámec); Přepínač (popis a fungování, přepínání, přepínací tabulka, VLAN)

Účel linkové vrstvy

poskytuje spojení mezi dvěma sousedními systémy
uspořádává data z fyzické vrstvy do logických celků – rámců
hlídá integritu (bezchybnost) dat pomocí kontrolních součtů

MAC adresa

Jednoznačně určuje zařízení v lokálním měřítku (v konkrétní Ethernetové síti). Adresa je přiřazena zařízení při jeho výrobě (spousta dnešních systémů ji však umí měnit).

Struktura MAC adresy

MAC adresa se skládá z 12 čísel v hexadecimální soustavě. Je rozdělena do 6 oktetů. Každý oktet obsahuje 8 bitů.

První 3 oktety se používají jako unikátní identifikátor výrobce. Jsou přiřazeny každé organizaci nebo prodejci. Toto přiřazení dělá Výbor registrační autority IEEE. Příklady:

CC:46:D6 - Cisco
3C:5A:B4 - Google, Inc.
3C:D9:2B - Hewlett Packard
00:9A:CD - HUAWEI TECHNOLOGIES CO.,LTD

Zbylé 3 oktety jsou využívány výrobci NIC (Network Interface Controller - síťová karta). Výrobci zde mohou použít jakoukoliv kombinaci znaků, ale prefix (první 3 oktety) by měly vždy zůstat takové, jaké bylo přiřazení od IEEE.


obr. 1: Struktura MAC adresy
Dostupné z: https://www.javatpoint.com/what-is-mac-address

Rámec

Jedná se o základní stavební blok síťové komunikace v rámci určité LAN. Pokud zařízení A komunikuje se zařízením B, tak je tato komunikace vedena v podobě toho, že si mezi s sebou posílají pakety, jež jsou součástí rámců (rámec je obsahuje ve své datové části).

Rámec obsahuje jak MAC adresu zdrojového zařízení, tak adresu cílového zařízení. Dále obsahuje IP adresy zdrojového i cílového zařízení. Součástí rámce jsou i samotná data, jež chceme přenést. Části rámce, jež obsahuje IP adresu cílového/zdrojového zařízení a data, říkáme packet.

Na základě toho, jakým standardem IEEE 802.xx (xx je číslo označující verzi standartu) je rámec daný, může být jeho struktura mnohem složitější. Základ však zůstává stejný.

Pro kontrolu toho, zdali dorazil rámec v pořádku slouží kontrolní součet jež je obsažený v samotném rámci. Opětovné přepočítání kontrolního součtu musí souhlasit s tím, který je v rámci uvedený.


obr. 2: Struktura MAC rámce
Dostupné z: https://www.javatpoint.com/what-is-mac-address

Přepínač (Switch)

Účelem přepínače je nasměrovat data do zařízení, kterému jsou určena na základě MAC adresy. Zařízení, jež jsou připojená k přepínači skrze jeho porty, tvoří síť.

Když přepínač příjme rámec, uloží zdrojovou MAC adresu (MAC adresa toho, kdo rámec poslal) do tabulky, zvané CAM (Content Addressable Memory; bývá také nazývána MAC tabulka) tabulka. Do této tabulky si také přepínač poznamená, k jakému portu se tato adresa váže.


obr. 3: CAM tabulka

Poté se přepínač podívá do této tabulky a najde si cílovou MAC adresu. Přepínač tedy ví, na jaký port má rámec přeposlat.

Ale co když cílová adresa v tabulce není? Přepínač pak pošle rámec na všechny své porty.


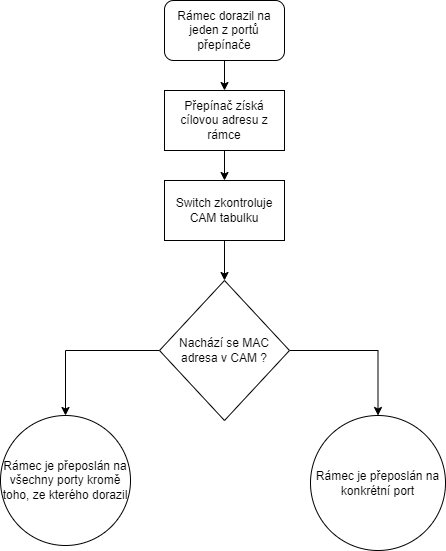obr. 4: Proces přeposlání rámce

Tím, že přepínač zašle rámec na všechny porty docílí toho, že rámec přijme zařízení, kterému je určeno. Toto zařízení bude pravděpodobně chtít odpovědět a jakmile do přepínače dorazí rámec od tohoto zařízení, tak si přepínač MAC adresu toho zařízení společně s portem poznamená.

VLAN

VLAN, nebo také virtuální LAN slouží k logickému rozdělení sítě nezávisle na fyzickém uspořádání. Můžeme tedy naši síť segmentovat na menší sítě uvnitř fyzické struktury původní sítě.

Pomocí VLAN můžeme dosáhnout stejného efektu, jako když máme skupinu zařízení připojených do jednoho přepínače a druhou skupinu do jiného přepínače. Jsou to dvě nezávislé sítě, které spolu nemohou komunikovat (jsou fyzicky odděleny). Pomocí VLAN můžeme takovéto dvě sítě vytvořit na jednom přepínači.

Důvody zavedení VLAN

seskupování uživatelů v síti podle skupin či oddělení nebo podle služeb místo podle fyzického umístění a oddělení komunikace mezi těmito skupinami
snížení broadcastů v síti
zjednodušená správa - k přesunu zařízení do jiné sítě stačí překonfigurovat zařazení do VLANy, tedy správce konfiguruje SW (zařazení do VLAN) a ne HW (fyzické přepojení)
zvýšení zabezpečení - oddělení komunikace do speciální VLANy, kam není jiný přístup. Toho se dá samozřejmě dosáhnout použitím samostatných přepínačů, ale s využitím virtuálních LAN nám k tomu může postačit jen jeden

Komunikace mezi VLAN

Konkrétní VLAN se aplikuje na jednotlivé porty. Pro každou VLAN, která je nakonfigurována na přepínači je separátní CAM tabulka.


obr. 5: MAC tabulka pro určitou VLAN
Dostupné z: https://lemp.io/a-switch-with-multiple-vlans-will-have-multiple-cam-tables/

Zařízení, která jsou v té samé VLAN tedy mohou komunikovat spolu. Avšak, zařízení, kde je každé v jiné VLAN, se nevidí. Pokud chtějí tyto zřízení komunikovat spolu, musí být tato možnost nakonfigurována na routeru, nebo přepínači, jež se nacházejí na síťové vrstvě. Říká se tomu routing mezi VLAN (Síťová vrstva).

Problém nastává, pokud máme propojené 2 přepínače a tyto přepínače mají k sobě připojená zařízení, jež jsou v těch samých VLAN. Dvě zařízení se mohou nacházet ve stejné VLAN, ale každé zařízení může být připojené k jinému přepínači. Toto řeší tzv. trunk port. Jedná se o port, ke kterému může být přiřazeno více VLAN.


obr. 6: Příklad sítě s využitím VLAN
Dostupné z: https://www.samuraj-cz.com/clanek/vlan-virtual-local-area-network/

Pro komunikaci mezi přepínači s využitím VLAN se využívá tzv. tagování rámců. Pokud posíláme rámec, chceme vědět, do jaké VLAN tento rámec spadá (chceme to vědět i na druhém přepínači, kterému tento rámec skrze trunk přijde).

Tomuto procesu se říká IEEE 802.1q tagging, který je umožněný protokolem IEEE 802.1q. Pokud je komunikace vedena skrze trunk port, tak je rámec upraven tak, že je mu přidána informace o tom, do jaké VLAN patří. Nakonec se přepočítá kontrolní součet.


obr. 7: Struktura rámce při přenosu skrze trunk port
Dostupné z: https://www.samuraj-cz.com/clanek/vlan-virtual-local-area-network/

Cisco ještě před existencí standardu IEEE 802.1q vytvořilo vlastní standard, kdy se celý rámec zabalí do nového.

Zdroje

Javapoint. What is MAC Address? [online] @2021. [citováno: 04.05.2023]
Dostupné z: https://www.javatpoint.com/what-is-mac-address
Cloudflare. WWhat is a network switch? [online] @2023. [citováno: 04.05.2023]
Dostupné z: https://www.cloudflare.com/learning/network-layer/what-is-a-network-switch/
ComputerNetworkNotes. How Switches Forward Frames Explained [online] @2019. [citováno: 04.05.2023]
Dostupné z: https://www.computernetworkingnotes.com/ccna-study-guide/how-switches-forward-frames-explained.html
Samuraj-cz.com. VLAN - Virtual Local Area Network [online] @2007. [citováno: 04.05.2023]
Dostupné z: https://www.samuraj-cz.com/clanek/vlan-virtual-local-area-network/
Lemp. A SWITCH WITH MULTIPLE VLANS WILL HAVE MULTIPLE CAM TABLES. Morales. [online] @2022. [citováno: 04.05.2023]
Dostupné z: https://lemp.io/a-switch-with-multiple-vlans-will-have-multiple-cam-tables/

Síťová (Internetová) vrstva IPv4

(adresa, hlavička, maska, unicast, multicast, broadcast, zápisy, distribuce IP); Základy směrování (popis, princip, TTL, gateway, Djikstra & Belmann-Ford)

Jedná se o protokol síťové vrstvy využívající další služební protokoly ARP, RARP, ICMP, IGMP a IPsec.

Tento protokol přepravuje data bez záruky. Záruku a kontrolu integrity přenechává na vyšší transportní vrstvě TCP.

RARP je v dnešní době nahrazen protokolem DHCP.

IP Datagram

IP datagram se skládá ze ZÁHLAVÍ a Datové části. Obě tyto části se vloží do datové části Linkového rámce.

Formát IP datagramu vypadá následovně:


obr. 1: IP datagram
zdroj: Přispěvatelé Wikipedie, IPv4 [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 29. 04. 2023, 17:57 UTC, [citováno 17. 05. 2023] https://cs.wikipedia.org/w/index.php?title=IPv4&oldid=22749106

verze protokolu = (0x4)
IHL - délka záhlaví
typ služby - klasifikace paketu (způsob a rychlost dopravy do místa určení) a ECN (co s paketem v případě zahlcení sítě - zda pakety zahodit)
celková délka - délka datagramu v bajtech (zde 2B)
identifikace - každý datagram má jednoznačný identifikátor, je-li datagram fragmentován, pozná se, které fragmenty patří k sobě
příznaky - řízení fragmentace, první fragment je vždy 0, druhý se značí DF (do not fragment) a třetí MF (more fragments); poslední fragment nastavuje zda není fragmentem posledním
offset fragmentu - udává na jaké pozici v původním datagramu fragment začíná
TTL - každý směrovač snižuje o 1, poslední směrovač, který sníží hodnotu na 0 DTG zahodí a pošle protokolem ICMP zprávu o zahození (poslední směrovač vrací echo request)
číslo protokolu - určuje jakému protokolu vyšší vrstvy se mají data předat
kontrolní součet hlavičky - ověří zda datagram není poškozený, pokud ano, je DTG zahozen
zdrojová adresa - adresa odesílatele (32 bitů)
cílová adresa - IP adresa rozhraní, pro které je DTG určen
nepovinné položky záhlaví

Fragmentace DTG


obr. 2: Fragmentace paketu
zdroj: DOSTÁLEK, L. Youtube. Počítačové sítě 06 IP IPv4.[online] [cit. 16-05-2023] Dostupné z: https://www.youtube.com/watch?v=8PRkgDOHfkI

Ethernet umí transportovat pouze pakety o velikosti 1500 (MTU). Každý fragment má svoje záhlaví, ale mění se offset, posléze délka a příznak u jednotlivých fragmentů.

IGMP

Protokol pro skupinové oběžníky (určeny jen pro některé stanice) na LAN. Protokol slouží jen k tomu, jak se má oběžník šířit po mé lokální síti.

3 typy paketu:

typ 16, ten posílá počítač na svůj směrovač s požadavkem na členství ve skupině - odběr multicastu (třeba radio);
typ 17 - opuštění členství ve skupině;
typ 11 - dotaz směrovače do LAN zda ještě někdo nechce poslouchat radio (multicast);

IP adresa, Maska, síť, sub-síť a supersíť

IP adresa

jednoznačně identifikuje každý interface v síti, která používá IP protokol
skládá se vždy ze dvou částí:
- adresa sítě (případně podsítě)
- adresa rozhraní
4B velikost (32 bitů)
historicky rozdělené do tříd A, B, C, D, E
- označovali kolik bitů je určeno pro síť
pro intranety máme speciální adresy

TŘÍDA	ADRESA	ROZSAH
Třída A	10.0.0.0/8	10.0.0.0 až 10.255.255.255
Třída B	172.16.0.0/12	172.16.0.0 až 172.31.255.255
Třída C	192.168.0.0/16	192.168.0.0 až 192.168.255.255


obr. 3: Třídy IP
zdroj: Přispěvatelé Wikipedie, Třídy IP adres [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 8. 03. 2023, 10:32 UTC, [citováno 18. 05. 2023] https://cs.wikipedia.org/w/index.php?title=T%C5%99%C3%ADdy_IP_adres&oldid=22526161

Distribuce IP

na vrchu pyramidy je organizace IANA, která dohlíží na přidělování IP
- IANA alokuje bloky adres do Regional Internet Registry
- svět je rozdělen na oblasti a každá RIR přiděluje IP ve své oblasti směrem k Internet Service Providerům (ISP)


obr. 4: Regional Internet Registry
zdroj: In: Juniper Networks: BGP Origin Validation Using Resource Public Key Infrastructure [online]. US, 2020 [cit. 2023-05-18]. Dostupné z: https://www.juniper.net/documentation/en_US/release-independent/nce/topics/concept/nce-187-bgp-rpki-technical-overview.html

Typy adres

unicast - odesílatel adresuje pro konkrétní interface
multicast - odesílatel adresuje skupině adresátů
broadcast - adresují se všichni adresáti v LAN
- funguje pouze u LAN
- funguje pouze u IPV4
anycast - adrsuje se více interfacům, ale DTG stačí doručit jen jednomu
- funguje pouze u IPV6

Unicast

jednoznačná adresa interface (16 bajtů)
- adresa sítě (64 bitů)
- adresa interface (64 bitů)
2 typy:
- globálně jednoznačné
- lokálně jednoznačné


obr. 5: Unicast
zdroj: DOSTÁLEK, L. Youtube. Počítačové sítě 08 IP adresa.[online] [cit. 16-05-2023] Dostupné z: https://www.youtube.com/watch?v=hh7DImZB60A

Multicast

metoda přeposílání IP DTG z jednoho zdroje více adresátům
místo odeslání jednotlivých DTG, je odeslán pouze jediný DTG, jediným datovým tokem, přes směrovače
pro účely multimédií a nebo oprav chyb OS apod.
cílem je zmenšení zátěže vysílajícího uzlu a přenosové sítě

Přenos dat v multicast

zařízení v síti se přihlásí do některé ze skupin - Multicast Group - pro zachytávání dat (třeba sledování videa)
router sítě musí multicast podporovat
- pokud podporuje, tak v sobě udržuje tabulku skupin
- router se periodicky dotazuje do LAN, zda existuje stanice, která chce informace ze skupiny odebírat
- router také naslouchá stanicím, které mu přes IGMP protokol pošlou zprávu "Membership report" s IP adresou třídy D (přidají se do skupiny) nebo "Leave Group"

Broadcast

šíření informace pro všechny interface
sdílení v síti MS, nebo identifikace zařízení
typy broadcast
- MAC broadcast
  - MAC adresa ve tvaru FF:FF:FF:FF:FF:FF
- IP broadcast
  - IP adresa broadcastu je 192.168.0.255
- síťový broadcast
  - IP DTG odeslán na adresu, která je v cílové síti broadcastem

Maska sítě

říká nám do které sítě IP adresa spadá
rozdělí IP na dvě části, adresu sítě a adresu interfacu na této síti
255.255.255.0 - část určena pro síť
255.255.255.0 - část určena pro zařízení v síti
lze zapsat i takto IP/24
část za lomítkem zachycuje počet bitů s log. jedničkou MASKY zleva, nebo také, kolik log. jedniček máme (do maximální hodnoty 32) pro jednotlivá zařízení

Adresa sítě

zjistíme ji log. operací AND IP adresy a Masky sítě

Supersíť a sub-síť

supersíť může zahrnovat naši síť
maska má méně bitů s log. jedničkami (tj. více prostoru pro interfejs -> naši síť)
sub-síť pod naší sítí má naopak masku s větším počtem log. jedniček (je tam méně prostoru pro interfejsi)

Směrování

Problém je založen na tom, že chceme-li z místní sítě odeslat paket na druhou stranu světa, nebo přes ulici, tak směrovače (routery) se musí rozhodnout, jakou linkou data vedou k adresátovi.

Cílem je doručit datagram co nejefektivněji k adresátovi.

Jelikož jsou cesty k adresátům vzhledem k velikosti sítě složité, řeší se pouze vždy jeden krok, a tedy, komu datagram předat jako dalšímu. Je to obdobné jako jízda autem, na křižovatce se rozhodnu dle značení, kam odbočím a na další křižovatce se opět rozhoduji dle značení. Nemám na první křižovatce všechna značení až do cílové cesty - křižovatka by byla přehlcená. Totéž by platilo o směrovači, kdyby měl uchovávat všechna data pro celou cestu až k adresátovi.

Směrovací protokoly

Interior Gateway Protocol (L1)
- IS-IS (linková vrstva)
- OSPF (zapouzdřený v IP)
Interior Gateway Protocol v2 (L2)
- RIP
- RIPv2
- IGRP
Exterior Gateway Protocol
- BGP
- Path Vector Routing Protocol

Směrovací tabulka

uložena ve směrovači
obsahuje seznam cílových sítí a rozhraní, za nimiž se sítě nachází

adresa cílové stanice se vynásobí maskou
porovná se s hodnotou v prvním sloupci, pokud odpovídá adrese sítě, nacpe se DTG do daného rozhraním (uvedený v témže řádku)
pokud adresa neodpovídá, postoupíme o řádek níže


obr. 6: Routovací tabulka
zdroj: DOSTÁLEK, L. Youtube. Počítačové sítě 09 IP Routing.[online] [cit. 16-05-2023] Dostupné z: https://www.youtube.com/watch?v=i5AJ4EdInWg

poslední řádek tabulky označuje default gateway
Metrika nám říká, která z cest se zvolí, pokud budeme mít dvě stejné cesty
v OS (WIN) vypíšeme RT pomocí příkazu: netstat -r

Do RT se adresy dostanou buď:

ručně
dynamicky (směrovacím protokolem)
tím, že daná stanice má nakonfigurovanou adresu a masku administrátorem (nejběžnější)

RVP - routing vector protocol (Bellman-Ford algoritmus)

Směrovací protokol funguje následovně:

řekněme, že se zapnou všech a zařízení v síti
- routery mají nakonfigurované interface
- počáteční konfigurace vytvoří položky v RT
směrovače si se svými sousedy vymění RT
RT na jednotlivých směrovačích se doplní o hodnoty ze sousedních směrovačů
- zvětší se o 1 metrika u nově obdržených položek
opět si vymění informace - dle RT již nesousedí s prvním prvkem vedle, ale se vzdálenějším (v korku 3 se totiž doplnili o blízkých sousedech info)
- metrika se opět zvýší u nových hodnot o 1
opět si směrovače vymění RT a všichni mají info o všech

Každé položce v RT se říká vektor, proto RVP.

Problém RVP spočívá v tom, že vypadne-li spojení mezi sítí a směrovačem, tak první směrovač u dané sítě ví, že spojení je přerušeno, tak si položku o dané síti vymaže. Nicméně, druhý směrovač měl přístup do té samé sítě, ale s metrikou dvě, takže v další iteraci pošle tomu prvnímu směrovači záznam o předmětné síti a ten první směrovač si položku uloží, ale protože hje pro něj (jakoby) nová, tak ji nastaví metriku 3.

Tím pádem si první směrovač myslí, že za směrovačem 2 je síť (pro kterou má tento první směrovač přiřazenou metriku 3), ale ve skutečnosti se jedná o onu zrušenou síť. Takto se záznam neustále cyklí a zvyšuje se metrika.

Například protokol RIP nastavuje limit pro metriku, je-li metrika sítě 15 považuje se za nedostupnou.

LSP - link state protocols a Dijkstra

Řeší problémy RVP protokolů. LSP jsou založeny na Dijkstrově algoritmu (hledání nejkratší cesty).

uzavřená oblast
routery vytvoří graf
každý směrovač hleda shortest path pro DTG
linky mezi Routery jsou hrany grafu
každá linka je hodnocena metrikou

router zjistí svoje sousedy (určí hrany a dle PINGU ohodnotí metrikou)
router rozešle info z kroku jedna všem sousedům v dané oblasti
každý uzel v oblasti zná kompletní topologii grafu
každý uzel si doplní do RT nejkratší cestu k dalšímu uzlu (k jeho lokální síti)

OSPF směrování

Open short path first je nejpoužívanějším protokolem pro směrování uvnitř autonomních systémů. Nevýhodou je, že má jasně danou topologii.

Základem topologie je páteřní síť (značí se 0.0.0.0 - 4B, ale jen připomínají IP) k níž se připojují další oblasti.

Pahýlová oblast má pouze jeden hraniční směrovač s páteřní oblastí.


obr. 7: OSPF topologie
zdroj: DOSTÁLEK, L. Youtube. Počítačové sítě 09 IP Routing.[online] [cit. 16-05-2023] Dostupné z: https://www.youtube.com/watch?v=i5AJ4EdInWg

Princip
OSPF je založen na tom, že každý Router zná topologii celé sítě (oblasti). Směrování má 3 kroky:

Správa sousedských relací
- relace mezi dvěma směrovači z jiných oblastí (sdílí L2 topologii)
Šíření směrových informací
- změnou se rozumí vznik nebo zánik sousedské relace
- routery uvnitř oblasti ví vše
- routery mimo oblast pouze případnou změnu metriky nebo směru
Určení nejkratší cesty (Dijsktra)

Autonomní oblast

v její rámci probíhá směrování pomocí interior gateway protokolů (viz výše). Pro externí komunikaci slouží exterior gateway protocol. Na hranici AS je tzv. hraniční router.

Hraniční router ve své RT nese dva typy informací:

z interior protokolu
z exterior protokolu

Poslání infa do další AS se nazývá právě Šíření směrových informací.


obr. 8: Komunikace AS to AS
zdroj: DOSTÁLEK, L. Youtube. Počítačové sítě 09 IP Routing.[online] [cit. 16-05-2023] Dostupné z: https://www.youtube.com/watch?v=i5AJ4EdInWg

Pojem Gateway a Default Gateway

Gateway

název síťového uzlu
propojuje dvě sítě pracující s odlišnými komunikačními protokoly
vykonává i funkci routeru
v hierarchii aktivních zařízení má nejvyšší postavení - stojí i nad směrovačem

Default Gateway

tzv. implicitní brána - označuje router, přes který se stanice připojují do vnější sítě

ZDROJE

https://www.youtube.com/watch?v=i5AJ4EdInWg
https://www.youtube.com/watch?v=hh7DImZB60A
https://www.youtube.com/watch?v=U5W8-gGblXs
https://www.youtube.com/watch?v=xr1u3LUwcek
https://www.youtube.com/watch?v=8PRkgDOHfkI
https://cs.wikipedia.org/wiki/Sm%C4%9Brov%C3%A1n%C3%AD
https://en.wikipedia.org/wiki/Bellman%E2%80%93Ford_algorithm
https://cs.wikipedia.org/wiki/Gateway
https://cs.wikipedia.org/wiki/Autonomn%C3%AD_syst%C3%A9m

Síťová (Internetová) vrstva IPv6

adresa, pravidla zápisu, rozdíly oproti IPv4, anycast, stavová/bezstavová konfigurace, metody tvorby IPv6 adresy, specifické IPv6 adresy, objevování sousedů, IPv6-IPv4/VLAN mapping, privacy extensions, přechodové mechanismy, bezpečnost

IPv6 je protokol síťové vrstvy, který umožňuje komunikaci po síti. Jedná se o nástupce IPv4 protokolu. V dnešní době je IPv4 pomalu vytlačován IPv6.

Rozdíly oproti IPv4 aneb proč byla nutná změna

Starší protokol IPv4 poskytuje pouze omezené množství adres. Adresní prostor IPv4 je 2³² adres, což je něco přes 4 miliardy. Prakticky je toto číslo menší kvůli sdružování adres do podsítí skrze masku sítě a část adres je rezervována pro speciální využití.

Protokol IPv4 též přestává vyhovovat z hlediska rychlosti přenosu dat, hlavně u multimediálních datových přenosů (videokonference, internetová TV, audiohovory apod.)

Hlavní změnou IPv6 oproti IPv6 je mnohem větší adresní prostor. Jedná se o 3.4 * 10³² různých adres. Pro představu na každého člověka na zemi připadá potenciálních 5x10²⁸ adres, nebo také 2⁵² pro každou známou hvězdu ve vesmíru. Zatímco u IPv4 je to pouze 0,5 adresy na člověka -> ano, počet IPv4 již byl dávno vyčerpán (poslední adresní prostory byly rozděleny v roce 2011).

Přečíslování sítě při změně poskytovatele internetu je s IPv4 obtížný proces. U IPv6 je mnohem jednodušší -> stačí změnit prefix sítě. V adresním prostoru IPv6 existuje možnost přidělit tzv. provider independent rozsahu, který je zcela nezávislý na poskytovateli a je přidělen přímo koncovému uživateli.

Díky takto velkému adresnímu prostoru již není potřeba NAT, který byl zaveden kvůli vyčerpání prostoru IPv4 adres a kvůli bezpečnosti.

IPv6 dále na rozdíl od IPv4 umožňuje tzv. bezestavovou konfiguraci (SLAAC). Host si může vzít svojí vlastní adresu bez nutnosti použití DHCP protokolu.

Většina protokolů ostatních vrstev podporuje IPv6 (TCP, UDP, ...). Problémy nastávají, pokud IPv6 není podporované.

IPv6 adresa a pravidla zápisu

IPv6 adresa je složena z 128 bitů a můžeme ji rozdělit na dvě části:

64 bitový síťový prefix
64 bitová část hosta

Část hosta je vytvářena na základě MAC adresy koncového uživatele nebo přiřazena následně. To vytváří bezpečností riziko neboť je možné vystopovat koncové zařízení, jež odpovídá MAC adrese rozhraní.

řešení je v podobě mechanismu, který mění kus IPv6 adresy

Notace

IPv6 je zapsaná jako 8 čtveřic čísel v hexadecimálním tvaru.

Například tedy: 2001:0db8:85a3:08d3:1319:8a2e:0370:7334

pokud je jedna nebo více po sobě jdoucích skupin 0000 tak mohou být nuly vynechány
- adresa 2001:0db8:85a3:0000:0000:0000:0370:7334 Může být tedy zkrácena na 2001:0db8:85a3::0370:7334
stejně tak můžou být vynechána počáteční nuly každé čtveřice

Následující adresy jsou si rovnocenné:

2001:0db8:0000:0000:0000:0000:1428:57ab
2001:0db8:0000:0000:0000::1428:57ab
2001:0db8:0:0:0:0:1428:57ab
2001:0db8:0:0::1428:57ab
2001:0db8::1428:57ab
2001:db8::1428:57ab

Poslední 4 bajty IPv6 adresy mohou být uvedeny v desítkové soustavě za použití tečky jako oddělovače. Toto je často uváděno v kompatibilních adresách.
IPv6 adresu lze namapovat na IPv4 adresu, například ::ffff:10.120.78.40

Notace sítě

Síť v IPv6 je popsána pomocí notace CIDR.

IPv6 síť (nebo podsíť) je skupina blízkých adres, jejíž velikost je mocnina čísla 2.
počáteční bity adresy jsou stejné pro všechny hosty sítě -> toto nazýváme prefixem sítě
síť je označena první adresou v sítí a lomítkem oddělenou délkou prefixu v bitech (desítkově)
- například 2001:0db8:1234::/48 označuje síť s adresami od 2001:0db8:1234:0000:0000:0000:0000:0000 do 2001:0db8:1234:ffff:ffff:ffff:ffff:ffff
- host se někdy označuje s lomítkem /128, protože ho můžeme chápat jako síť s prefixem dlouhým 128 bitů (sít pro jedno zařízení)
routování je totožného principu, jako je tomu v případě IPv4, jediný rozdíl je v délce adresy v bitech

Druhy adres

Adresy IPv6 můžeme dělit na:

unicast
- identifikují jedno jediné rozhraní
multicast
- identifikují skupinu rozhraní
- mají prefix FF00::/8 a její druhý oktet určuje dosah adresy -> rozsah, v jakém je tato multicast adresa zviditelněna
anycast
- je podobná multicastu s tím rozdílem, že vyslaný packet dorazí pouze jednomu zařízení, obvykle tomu nejbližšímu s pohledu směrovače
- anycast adresy jsou nerozlišitelné od unicast adres
- pokud přiřadíme unicast adresu více rozhraním, jedná se o anycast

Dále máme několik vyhrazených IPv6 adres. Tyto adresy mají speciální význam:

Místní linka
- ::1/128 adresa místní smyčky, je náhradou za localhost -> packet vyslaný na tuto adresu je vrácen zpět
ULA (Unique Local Adress)
- fc00::/7 jedná se o unikátní lokální adresy, jsou směrovatelné pouze v podmnožině spolupracujících sítí
- adresy zahrnují 40-bitové pseudonáhodné číslo minimalizující konflikty při sloučení sítí nebo úniku packetů
IPv4 (speciální adresy)
- ::ffff:0:0/96 používá se přechodových mechanismů
- 2002::/16 používá se u IPv6 -> IPv4 tunelů
Multicast
- ff00::/8 použití pro multicast adresy

Adresování

Pži adresování dělíme síť na tři části:

site prefix (48 bitů)
- prefix sítě, popisuje veřejnou topologii, je přidělený poskytovatelem internetu (ISP)
subnet prefix (16 bitů)
- prefix podsítě, specifikuje rozsah interní topologie (možnost vytváření podsítí, můžeme se na to koukat jako na prefix určující lokální síť)
- je náhradou za subnetting v IPv4
interface ID
- také se mu říká token, jedná se o číslo, určující konečně zařízení


obr. 1: Rozdělení IPv6 adresy při adresaci
zdroj: https://docs.oracle.com/cd/E18752_01/html/816-4554/ipv6-overview-10.html

Přidělování IPv6 adres

site prefix je přidělený ISP
subnet prefix je přidělený administrátorem sítě
adresa rozhraní hosta (zbytek) je přidělena tedy jak?

Jde to pomocí tří způsobů:

statická konfigurace (manuální přidělení adresy)
dynamická konfigurace
- stavová
- bezestavová

Stavová a bezestavová konfigurace

Stavová konfigurace

Jedná se o konfiguraci pomocí DHCPv6, což je upravený DHCP protokol pro IPv6 adresování.

od svého předchůdce se moc neliší
poskytuje adresu s předem vybraného rozsahu
je podmíněný podporou UDP komunikace na obou zařízeních
princip výměny 4 zpráv zůstává
- zažádání klientem o adresu
- zasláni volných adres ze serveru
- vybrání adresy klientem
- potvrzení od DHCP serveru

Bezestavová konfigurace (SLAAC)

specifické pro IPv6

Jedná se o metodu která přiděluje hostovi adresu automaticky, nebo pokud si o ni požádá. Využívá toho, že v každé podsíti se nachází směrovač nebo server, který ji propojuje s okolním světem. Tyto parametry poté směrovač nebo server rozesílá do všech k němu připojených sítí.

Tyto parametry jsou rozesílány v podobě ICMPv6 zprávy.

Ve stručnosti:

Před zahájením komunikace si každý uzel (host) vygeneruje svoji local-link adresu pro každý port, která začíná prefixem FE80::/10 a připojí k tomu identifikátor rozhraní.
Host nyni musí ověřit unikátnost tohoto rozhraní v rámci lokální sítě. Použije k tomu mechanismus hledání duplicitních adres za pomocí vyhledávání sousedů (viz dále).
Pokud dorazí ohlášení souseda tak to znamená, že nějaký jiný host v síti má stejný identifikátor rozhraní a automatická konfigurace je zastavena. V případě negativního ohlášení si host vygenerovanou local-link adresu přidělí a čeká na ohlášení směrovače/serveru.
Ohlášení směrovače/serveru uzlu říká, jestli nyní má použít stavovou, nebo bezestavovou konfiguraci.
Stavová konfigurace jest popsána zde.
V ohlášení jsou uvedené prefixy (to jsou ty porty hosta), ke kterým host přidělí svůj dříve vygenerovaný identifikátor (local link adresu?). Dále je v ohlášení uvedeno, jak dlouho bude identifikátor platný, než bude potřeba vytvořit nový.

Celý SLAAC je velmi složitý. Je popsaný společně se strukturou ohlášení od směrovače/serveru zde.

Objevování sousedů

Jedná se o protokol s označením NDP (Neighbor Discovery Protocol). Protokol definuje 5 různých ICMPv6 paketů, jež vykonávají funkce pro IPv6 podobným způsobem, jako pracuje v IPv4 protokol ARP, ICMP router discovery a ICMP redirect.

Používá se pro autokonfiguraci síťových rozhraní

Definuje tedy 5 různých ICMPv6 typů paketů:

Router Solicitation
- host se snaží pomocí této zprávy najít router
Router advertisement
- směrovač touto zprávou ohlašuje svoji přítomnost a posílá různé linkové a internetové parametry buď periodicky nebo v reakci na router solicitation
Neighbor solicitation
- tyto zprávy jsou používány hosty k určení adresy ke komunikaci se sousedem nebo k ověření, že je soused dosažitelný
Neighbor advertisement
- používaná jako reakce na neighbor solicitation
Redirect
- směrovač pomocí této zprávy informuje hostitele, že existuje lepší první hop na cílový směrovač

Tyto zprávy mohou být použity pro následující funkce:

Router discovery: hostitelé mohou najít směrovače umístěné na připojených linkách.
Prefix discovery: hostitelé mohou zjistit prefixy adres, které jsou připojené na lince.
Parametr discovery: hostitelé mohou zjistit parametry linky (např. MTU).
Automatická konfigurace adres: volitelná bezstavová konfigurace adres síťových rozhraní.
Rezoluce Adres: mapování mezi IP adresami a adresami linkové vrstvy (MAC adresami).
Stanovení next–hop: hostitelé mohou najít další směrovače na místo určení.
Detekce nedostupnosti sousedních uzlů (NUD): určení, že soused již není na této lince dostupný.
Detekce duplicitních adres (DAD ): uzly mohou zkontrolovat, jestli je adresa už používaná.
Packet redirection: pro poskytnutí lepší next-hop cesty pro některá cílová místa.

IPv6-IPv4/VLAN mapping

pro IPv6 je povětšinou potřeba manuálně povolit (podporují pouze Cisco switche)
- celkově, řádné pracování s IPv6 je podporováno hlavně v rámci Cisca, ostatní organizace jsou dosti pozadu
- Cisco začalo plánovat adaptaci na IPv6 již v roce 2002

Jedná se o techniku, která umožňuje namapovat ID VLAN na jednom switchi na ID VLAN na jiném switchi. Tímto je možné referovat tu a samou VLAN pomocí různých VLAN ID na různých switch zařízeních.

Privacy extensions

Jedná se o formát, který definuje dočasné adresy, jež se mění v pravidelných časových intervalech

nová adresa vypadá, jako že nemá nic společného s tou starou pro kohokoliv zvenčí
jedná se o ochranu proti korelaci adres
regulární změna adres je nezávislá na prefixu sítě -> ochrana proti trackování pohybu po síti (útočník musí najít vygenerovanou pseudo-adresu namísto statické)

Přechodové mechanismy

Jedná se o mechanismy, které umožňují IPv6 hostům využívat IPv4 služby a izolovaným IPv6 hostům a sítím dát možnost se pohybovat skrze IPv4 infrastrukturu (například NAT).

Tyto mechanismy jsou například:

duální implementace
- protože IPv6 rozšiřuje IPv4, je možné vytvořit síťovou implementaci které podporují oba dva protokoly
- host využívající tuto implementaci se nazývá dual-stack host
tunelování (něco jako VPN)
- nejznámější je tunelování 6to4
  - koncové body jsou určeny známou anycast IPv4 adresou na místní straně a zapouzdřením IPv4 adresy do IPv6 adresy na vzdálené straně
- jiné používané tunelování je pomocí protokolu ISATAP
  - tento protokol považuje IPv4 místní síť za IPv6 virtuální linku a mapuje všechny IPv4 adresy na IPv6 adresy místní linky
spravované tunelování
- koncové body tunelu jsou výslovně uvedeny, povětšinou lidským operátorem nebo službou zprostředkovatele tunelu
- hodí se pro velké sítě, protože je více deterministické než předchozí případy
- při tomto způsobu se do hlavičky IPv4 paketu přidává informace o protokolu číslo 41

Bezpečnost

jednotlivé datagramy je možno šifrovat pomocí protokolu IPSec
v IPv6 má každá stanice globálně dostupnou adresu (neexistuje NAT)
- je nutné nastavit hraniční firewall
- lze obejít tím, že uživatel si vytvoří vlastní tunel (třeba za pomocí VPN)
  - řešením je použít NAT64, což je nadstavba nad klasickým NAT, který ale umí pracovat s IPv6 adresami a schovává všechny zařízení v sítí za jednou adresou
  - stejně tak musí jít veškerá komunikace do internetu přes tento směrovač
využití DNS64
- jedná se o obdobu DNS, které je schopné pracovat s IPv6 adresami skrze NAT64
- směrovač odešle požadavek na DNS, DNS mu v případě IPv6 adresy vrátí chybu
- směrovač se poté zeptá na IPv4 adresu cílové služby
- tuto adresu namapuje na IPv6 adresu, jejíž prefix je daný směrovačem (jedná se o speciální prefix)
- takto zabalenou odpověď přepošle směrovač zpět klientovi
validaci příchozích zpráv do sítě provádí NAT64
- zabrání se tím označení příchozích namapovaných IPv6 zpráv jako podvržených

Zdroje

IPv6. Wikipedie: Otevřená Encyklopedie [online] @2023 [citováno 20.05.2023]
Dostupné z: https://cs.wikipedia.org/wiki/IPv6
What Is IPv6 (Internet Protocol Version 6)? Definition, Features, and Uses. Chiradeep BasuMallick [online] @2022 [citováno 20.05.2023]
Dostupné z: https://www.spiceworks.com/tech/networking/articles/what-is-ipv6/
IPv6 Addressing Overview. Oracle [online] @2023 [citováno 20.05.2023]
Dostupné z: https://docs.oracle.com/cd/E18752_01/html/816-4554/ipv6-overview-10.html
IPv6 Anycast Address. Cisco [online] @2023 [citováno 20.05.2023]
Dostupné z: https://www.cisco.com/c/en/us/td/docs/ios-xml/ios/ipv6_basic/configuration/xe-16-5/ip6b-xe-16-5-book/ip6-anycast-add-xe.pdf
Unique local address. Wikipedia: The Open Encyclopedia [online] @2023 [citováno 20.05.2023]
Dostupné z: https://en.wikipedia.org/wiki/Unique_local_address
Neighbor Discovery Protocol. Wikipedie: Otevřená Encyklopedie [online] @2023 [citováno 20.05.2023]
Dostupné z: https://cs.wikipedia.org/wiki/Neighbor_Discovery_Protocol
VLAN mapping configuration. h3c [online] @2023 [citováno 20.05.2023]
Dostupné z: https://www.h3c.com/en/Support/Resource_Center/EN/Home/Public/00-Public/Technical_Documents/Configure___Deploy/Configuration_Guides/H3C_CG-9254/03/202303/1790810_294551_0.htm
IPv6 Addresses, Security and Privacy. Ripe Labs [online] @2023 [citováno 20.05.2023]
Dostupné z: https://labs.ripe.net/author/johanna_ullrich/ipv6-addresses-security-and-privacy/
Bezpečnost protokolu IPv6. Nic.cz [online] @2023 [citováno 20.05.2023]
Dostupné z: https://www.nic.cz/files/nic/doc/Computerworld_IPv6_062011.pdf
Konfigurace adres při implementaci IP verze 6 v koncových sítích. L. Čepa, J. Kačer. České vysoké učení technické v Praze, FEL [online] @2012 [citováno 20.05.2023]
Dostupné z: http://access.feld.cvut.cz/view.php?cisloclanku=2012060001

Transportní vrstva

TCP (popis, TCP segment, hlavička, navazování spojení, služby a porty, velikost okna); UDP (popis, UDP datagram, pseudo IPv4, kontrolní součet, služby a porty, výhody, nevýhody)

Transportní vrstva, se nachází mezi aplikační a síťovou vrstvou. Na aplikační vrstvě se nacházejí jednotlivé aplikace, které pracují s protokoly aplikační vrstvy.

SMTP (používaný pro posílání emailů)
HTTP (nejpoužívanější protokol pro webové stránky)
FTP (protokol pro přenos souborů)
a další....

Tyto protokoly komunikují s protokoly transportní vrstvy skrze porty. Můžeme říct, že porty tvoří spojení mezí aplikační a transportní vrstvou. Každý port je poté přiřazen k určitému protokolu na aplikační vrstvě. Protokol HTTP například využívá port s číslem 80. Porty využívají služby na aplikační vrstvě. Služba může být webová stránka, nebo i aplikace. Port může využívat buď TCP, nebo UDP spojení, popřípadě obojí.

Port je 16-bitová hodnota, jež může nabývat rozsahu 0 - 65535.

Porty můžeme dělit do 3 kategorií.

dobře známé
- porty v rozsahu 0 až 1023; vyhrazené pro nejběžnější služby
rezervované
- v rozsahu 1024 až 49151, použití portu by se mělo registrovat u ICANN (Internet Corporation for Assigned Names and Numbers)
dynamické a soukromé porty
- v rozsahu 49152 až 65535, vyhrazené pro dynamické přidělování a soukromé využití, nejsou pevně přiděleny žádné aplikaci

TCP (Transmission Control Protocol)

Základní popis

TCP přenáší packety, což jsou série bitů, které mají určité uspořádání. TCP protokol přidává k packetům další část, header. Packet, společně s headerem/hlavičkou se poté nazývá segment.

Pro navázání a udržování spojení skrze TCP se využívá 3 way handshake. Přijímající strana musí vždy potvrdit, že odeslanou zprávu přijala v pořádku. Pokud toto nepotvrdí, je segment odeslán znovu. (více dále)

TCP je označovaný jako spolehlivý protokol. TCP používá službu síťového protokolu IP opakovaným odesíláním ztracených nebo poškozených packetů/segmentů.

TCP segment

Segment je složený z dat aplikace a hlavičky kterou mu TCP přiřadilo.

Hlavička segmentu (header)

Header obsahuje informace o segmentu.


obr. 1: Struktura hlavičky TCP segmentu
Převzato z: http://www.myreadingroom.co.in/notes-and-studymaterial/68-dcn/850-tcp-segment.html

Zdrojový port
Cílový port
Sequence number (Sekvenční číslo)
- Hodnota v poli se chová jako čítač, který nám říká, kolik bytů bylo odesláno. Pokud máme packet, který obsahuje data o velikosti 1400 bytů, tak sequence counter bude inkrementovaný o tuto hodnotu po odeslání segmentu.
Acknowledgement number
- Pole obsahuje číslo, které říká, kolikátý packet příjemce očekává od odesílatele. Pokud příjemce úspěšně přijal číslo X od odesílatele, tak se ack number definuje jako x+1 (očekáváme následující packet). Pokud hodnota nesouhlasí, je packet pozdržen tak, aby byl předán ve správném pořadí.
HLEN
- Pole obsahuje číslo udávající velikost hlavičky. Ta může být 20 - 60 bytů.
Control flag
- Pole definuje celkem 6 různých příznaků. Každý příznak má jeden bit (ano/ne) a pole má celkem 6 bitů:
  - URG: označí data jako urgentní, nastavuje tomuto packetu vyšší prioritu
  - ACK: hodnota acknowledgment field (acknowledgment number) je validní
  - PSH: pošli data ihned jak je to možné (systém nebude čekat a bufferovat data), často se požívá v kombinaci s URG příznakem
  - SYN: synchronizuj sekvenční číslo během připojení
  - FIN: ukonči spojení
Velikost okna
- Definuje velikost v bytech, kterou musí druhá strana dodržovat. Délka tohoto pole je 16 bitů, takže maximální velikost okna je 65535 bytů. Tato hodnota je určována příjemcem. Odesílatel se musí přizpůsobit a odesílat packety jen takové velikosti, jakou udá příjemce pomocí této položky v hlavičce.
Kontrolní součet
- Používá se pro ověření poškození packetu při přijmutí. Příjemce znovu vypočítá z obsahu kontrolní součet. Pokud se neshoduje, je zažádáno o zaslání packetu znovu.
Options
- 40 bytů, nejčastěji obsahuje informace o maximální velikosti segmentu nebo časové razítko.

Navazování spojení

Navázání spojení, se provádí metodou, které se říká 3-Way handshake. Tento proces se skládá ze 3 částí.

SYN
SYN/ACK
ACK


obr. 2: 3-Way handshake
Převzato z: https://www.geeksforgeeks.org/tcp-3-way-handshake-process/

SYN
- Klient chce navázat spojení. Klient tedy odesílá segment, který obsahuje Synchronize Sequence Number, jež druhé straně říká, že někdo chce spojení navázat a jakým sekvenčním číslem budou segmenty začínat.
SYN/ACK
- Příjemce SYN segmentu odpovídá odesílateli s pozitivním ACK příznakem a sekvenčním číslem, kterým chce segmenty začínat.
ACK
- Příjemce SYN/ACK odesílá potvrzující zprávu. Po jejím přijetí druhou stranou může začít přenos dat.

Při samotném přenosu je zajištěna spolehlivá komunikace pomocí Positive Acknowledgement with Re-transmission (PAR). Princip spočívá v tom, že odesílatel posílá ten a samý segment do té doby, dokud neobdrží od příjemce acknowledgement. Pokud dorazili data v pořádku, tak ho dostane. Ale pokud jsou data na straně příjemce poškozena (kontrola pomocí kontrolního součtu), tak příjemce segment zahodí a neposílá acknowledgement. Odesílatel tedy znovu posílá segment, na který acknowledgement nedostal, dokud ho nedostane.

Ukončování spojení

Pro ukončení spojení se využívá 4-way handshake. Skládá se ze 4 částí.

Jeden z účastníků spojení posílá segment, ve kterém je FIN příznak nastavený na 1. Přeje si ukončit spojení.
Příjemce segmentu s FIN příznakem odesílá segment s ACK příznakem. Odesílatel FIN příznaku je nyní ve fází, kdy přijal ACK na jeho žádost o ukončení spojení a čeká.
Příjemce původního FIN příznaku nyní odesílá segment s FIN příznakem jako že si tedy také přeje ukončit spojení.
Odesílatel původního FIN příznaku odesílá ACK příznak a spojení je ukončeno.

Body 2 a 3 se mohou zdát, že by mohli být spojené do jednoho -> poslat FIN a ACK příznak najednou. To ale nelze z důvodů toho, že příjemce iniciální zprávy s FIN příznakem můž mít ještě nějaká data k odeslání. Před ukončením celého spojení by bylo vhodné tyto data odeslat, aby nedošlo ke ztrátě packetů.

Výhody a nevýhody TCP

Výhody:

bezpečný způsob přenosu dat -> vyžaduje potvrzení doručení každé zprávy, umožňuje přijmutí zpráv ve správném pořadí
může být použít ve velkém množství odvětvích přenosu dat po síti
může komunikovat s velkou škálou protokolů

Nevýhody:

spojení je časově náročné -> každá zpráva vyžaduje potvrzení a ukončení spojení není okamžitý proces

UDP (User Datagram Protocol)

Základní popis

UDP přenáší série bitů, které mají určité uspořádání. UDP přidává k přenášeným datům vlastní hlavičku, která je o proti TCP mnohem jednodušší. Takto přenášenému packetu pomocí UDP se říká datagram.

Na rozdíl od TCP je UDP takzvaně nespolehlivý protokol. K navázání spojení nepotřebuje žádnou odezvu od druhé strany. Vlastně nemůžeme úplně mluvit o navázání spojení, protože UDP protokolu je jedno, zdali datagram příjemci dorazí.

UDP, stejně jako TCP, používá k určení cíle zprávy porty. TCP a UDP mají svá číslování portů. Při komunikaci skrze UDP mluvíme o UDP portech.

UDP datagram

Stejně jako u TCP, je UDP datagram složený z dat a hlavičky.


obr. 3: Struktura UDP datagramu
Převzato z: https://cs.wikipedia.org/wiki/User_Datagram_Protocol

Kromě přenášených dat je součástí hlavička, která obsahuje 4 pole, z čehož dvě jsou volitelná.

Zdrojový port
- volitelný, pokud odesílatel neočekává odpověď na svoji zprávu, je hodnota nastavena na 0
Cílový port
Délka UDP packetu (datagramu)
- obsahuje hodnotu určující velikost UDP datagramu, včetně hlavičky, minimální hodnota je 8 bajtů
Kontrolní součet
- hodnota určující správnost přijatého packetu na straně příjemce
- tato hodnota je volitelná, ale téměř vždy se používá
- pokud příjemce obdrží datagram a po přepočtení kontrolního součtu se hodnoty neshodují, je datagram příjemcem zahozen
- protože používáme UDP, odesílatel to nikdy nezjistí

Výhody a nevýhoy

Výhody:

UDP nepotřebuje navazovat či udržovat spojení.
UDP používá malou velikost packetů (datagramů). Zpracování celého packetu je tedy mnohem rychlejší, než v případě UDP.
Může být použít pokud je zde pouze jeden packet, který je třeba přenést mezi klienty. Boradcast a multicast jsou dostupné pomocí UDP.
Kotrola příjmání/odesílání zpráv může být ponechána na uživatelských programech a může být implementována pouze v takové míře, v jaké je potřeba.

Nevýhody:

Nemáme jistotu, že data jsou doručena.
Nemáme jistotu, že data jsou přijímána ve stejném pořadí, jako jsou odeslána (TCP má toto zajištěné pomocí sekvenčního čísla).
Implementace flow controll (vzájemné komunikace) je čistě na uživatelské aplikaci (což může být i plus) -> UDP neposkytuje žádnou garanci. Packet mohl být doručen, ale i nemusel. Mohl být doručen dvakrát, packety mohli dorazit v chybném pořadí. Odesílatel nic z toho neví, pokud se mu to naslouchající program na druhé straně neuvolí říct (posláním UDP zprávy, například).

Pseudo IPv4

Počet IPv4 adres je značně omezený oproti IPv6 adresám. Některé služby využívají čistě IPv4 a klienti mohou mít problémy s připojením skrze IPv6.

Protokol byl vytvořený jako lightweight alternativa k IPv4 a IPv6 protokolům, podobně jako je UDP alternativa k TCP -> UDP neposkytuje téměř žádné transportní služby, na rozdíl od TCP. Pseudo IPv4 si tedy klade za cíl poskytovat minimum síťových služeb.

Pseudo IPv4 je síťový protokol, který mapuje IPv6 adresy na IPv4 adresy třídy E - (240.0.0.0 - 255.255.255.255). Toto nám dává 268,435,456 (250 milionů) možných IPv4 adres. Je to sice málo oproti 340 undecillionům možných IPv6 adres, ale pořád dost velké množství, které nevystačí jen těm největším webovým stránkám.

Třída E

Třída E se povětšinou nepoužívá, pouze ke specifickým účelům, je tedy ideální pro pokrytí potřeb převodu IPv6 na IPv4.

Princip mapování

Pseudo IPv4 používá hashovací algoritmus, který vezme prvním 64 bitů IPv6 adresy a převede je na IPv4 adresu třídy E. Tento algoritmus má pro stejný vstup vždy ten samý výstup, konkrétní IPv6 adresa je tedy vždy přemapována na stejnou pseudo IPv4 adresu.

Zdroje

Transmission Control Protocol. Wikipedie: Otevřená Encyklopedie [online] @2022 [citováno: 14.05.2023]
Dostupné z: https://cs.wikipedia.org/wiki/Transmission_Control_Protocol
Transmission Control Protocol (TCP). IBM [online] @2010 [citováno: 14.05.2023]
Dostupné z: https://www.ibm.com/docs/en/zos-basic-skills?topic=4-transmission-control-protocol-tcp
TCP 3-Way Handshake Process. GeeksForGeeks [online] @2022 [citováno: 14.05.2023]
Dostupné z: https://www.geeksforgeeks.org/tcp-3-way-handshake-process/
User Datagram Protocol. Wikipedie: Otevřená Encyklopedie [online] @2021 [citováno: 14.05.2023]
Dostupné z: https://cs.wikipedia.org/wiki/User_Datagram_Protocol
Pseudo-IP: Providing a Thin Network Layer Protocol for Semi-Intelligent Wireless Devices. Kevin C. Almeroth [online] @2014 [citováno: 14.05.2023]
Dostupné z: http://www.nmsl.cs.ucsb.edu/papers/DARPA-98.pdf
Eliminating the last reasons to not enable IPv6. Matthew Prince [online] @2014 [citováno: 14.05.2023]
Dostupné z: https://blog.cloudflare.com/eliminating-the-last-reasons-to-not-enable-ipv6/

Aplikační vrstva

Protokoly (DHCP, HTTP, FTP, POP3, IMAP, SMTP, SSH, SSH, TELNET); DNS (popis a pojmy, systém a hierarchie DNS, iterace, TLD, doména, DNSSEC, útoky)

Jedná se o poslední vrstvu (abstraktní), jejímž účelem je umožnit aplikacím na různých počítačích komunikovat mezi sebou.

Dle ISO/OSI je aplikační vrstva 7. vrstvou modelu, zatímco u modelu TCP/IP se jedná o 4 vrstvu.

Pro přenos dat pod aplikační vrstvou slouží TCP/UDP protokol, TCP garantuje přenos dat mezi aplikacemi (ztracený paket je zopakován), zatímco pomocí UDP se data buď doručí či nedoručí.

HTTP

Protokol určený pro komunikaci s WWW servery. Slouží pro přenos hypertextových dokumentů v HTML a XML. Jedná se také o bezstavový protokol, což znamená, že každý dotaz od uživatele/klienta je zpracován samostatně a bez návaznosti na předchozí.

Běžně běží na portu TCP/80.

S pomocí standardu MIME může http přenést jakýkoli soubor. Pro zjištění umístění zdroje v internetu používá tento protokol tzv. URL - Uniform Resource Locator.

Samotný protokol HTTP neumožňuje security, a proto se používá ve spojení s TLS (kryptografický protokol). Toto použití se označuje jako HTTPS.

Uživatel napíše do browseru http://cs.wikipedia.org
místní DNS přeloží jméno na IP a vrátí klientovi
prohlížeč naváže se serverem TCP spojení
prohlížeč pošle požadavek GET + specifikaci souboru, který chce obdržet + protokol, přes nějž chce soubor obdržet + hlavičku z jakého serveru to chceme
např.
GET /wiki/Wikipedie/ HTTP/1.1
Host: cs.wikipedia.org
User-Agent: Opera/9.80 (Windows NT 5.1; U; cs) Presto/2.5.29 Version/10.60
Accept-Charset: UTF-8*
odpovědí serveru je <výsledkový kód><poznámka>

např. HTTP/1.1 200 OK

 HTTP/1.0 200 OK
 Date: Fri, 15 Oct 2004 08:20:25 GMT
 Server: Apache/1.3.29 (Unix) PHP/4.3.8
 X-Powered-By: PHP/4.3.8
 Vary: Accept-Encoding,Cookie
 Cache-Control: private, s-maxage=0, max-age=0, must-revalidate
 Content-Language: cs
 Content-Type: text/html; charset=utf-8

Host se používá proto, že na portu TCP/80 může být hostováno vícero HTTP serverů.

Výsledkové kódy
1XX - informativní odpověď
2XX - úspěšná akce
3XX - přesměrování
4XX - chyba klienta (chyba v dotazu třeba)
5XX - chyba serveru

Proxy

Proxy je mezibodem mezi uživatelem a serverem (na cestě k serveru jich může být mnoho). Proxy se skládá z:

Klientské části
Serverové části
Vlastní logiky proxy

Uživatelský klient kontaktuje serverovou část proxy, ta předá info klientské části a ta kontaktuje jménem klienta/uživatele daný server.

Vnitřní logika proxy může sloužit jako filtr, který odfiltruje dle nastavených parametrů, jaké servery může uživatel kontaktovat či nikoli. Např. může být nastaveno, že nemůžeme na server Jakup.Schwarz.ug, tím pádem nás proxy nepustí dál.

Proxy má také vlastní CACHE, kam uloží data ze serveru (třeba obrázky). Při dalším dotazu může proxy vzít data rovnou z CACHE.

Uživatel v místní síti nekomunikuje s DNS serverem sám, ale prostřednictvím proxy, tedy do PROXY jde celá URL a proxy teprve rozkouskuje URL a dotazuje se jednotlivých DNS na překlad až poté naváže s cílovým serverem spojení.

URI - uniform resource identifier

Obecný identifikátor:

URL - konkrétní server i soubor/službu
URN - neřeší cestu ke zdroji

URI: <schéma>:<na schématu závislá část>
URL: //<'user>:<'password>@host<'port>'/<'url-path>

user a pw se většinou nevyužívá.

http://server.firma.cz případně (ale nepoužívá se) http://novak:heslo@firma.cz

nebo např: mailto:schwarzjakupbrundosemerek@ahoj.cz

V URI se mohou vyskytovat pouze znaky US-ASCII, pokud se zadává jiný znak, tak se escapuje %.

Metody HTTP

Slouží ke komunikaci mezi aplikacemi přes http.

GET - dotazování klienta na konkrétní info na serveru
POST- odesílá uživatelská data na server
HEAD - jako GET, ale požaduje hlavičku odpovědi bez dat (pouze metadata)
OPTIONS - jaké server podporuje metody
PUT - nahraje data na server
TRACE - zjistíme kolik je mezi námi a serverem bran a proxy - zjišťujeme co servery na požadavku mění
CONNECT - spojí se s uvedeným objektem přes daný port
DELETE - smaže uvedený objekt na serveru

Potřebuji držet relaci (e-shopy typicky). Protože HTTP je defaultně bezstavový.

Server při návštěvě webu přiřadí klientovi ID pomocí hlavičky Set-Cookie.

Server vrací cookie klientovi a on ji pak v dalších dotazech posílá serveru, aby server věděl, o koho se jedná a co si třeba v tom daném obchodě vybral.

Krok, kdy je klient již u pokladny a uživatel chce potvrdit objednávku obleku:

Client: POST / obchod/doprava HTTP/1.1
Client: Cookie: Version="1";
Zakaznik="007"; Path="/obchod";
Zbozi="sako_05"; Path="/obchod";
Doprava="dobirka"; Path="/obchod";

Může být přidán další parametr Domain="";
Na web se dostane například pomocí javascriptu s reklamou od reklamní agentury.

Používají se také analytická cookie.

HTTP/2.0

zpětná kompatibilita s HTTP/1.1
pipelining požadavků - možnost paralelně stahovat objekty ze stránky současně - streamy skrze jedno TCP spojení
TLS 1.2
Server Push - komunikaci aktivuje klient

DNS - Domain Name System

Jedná se o databázový systém distribuovaný po celém světě provozující Jmenné Servery. V podstatě překládá jména na IP adresy a obráceně.

Tedy, bubu-li chtít na seznam.cz, tak potřebuji nejprve kontaktovat DNS server, který mi přeloží název adresy na IP.

Domény jsou zachyceny ve stromové struktuře, jejímž kořenem je TEČKA ".".

Pod kořenovou doménou jsou tzv. TLD - Top Level Domain: arpa, cz, ua, uk, com.

Dále jsou domény 2. úrovně (cuni, jcu, siemens, firma apod.) a 3. úrovně (prf, brno, cbu).

Syntaxe: www.firma.cz. Pomlčku lze použít pouze uprostřed domény. Zároveň každý znak může být ASCII.

Dříve se v zemích, kde se nepoužívá latinka, ale třeba arabština, nebo hebrejština obsahovali často doménové názvy číslice. www.68-5412.com. Dnes je toto vyřešeno pomocí IDN - Internationalized Domain Names. To využívá Ponycode, který umí převést jakékoli znaky UniCode do ASCII znaků.

V ČR spravuje domény NIC.CZ. V EU je TLD .eu nebo totéž napsané v azbuce. Podporovány jsou tyto znakové sady (azbuka i novořečtina a latinka).

Překlady IPv4 zajišťuje .arpa -> .in-adrr. Adresy jsou napsány opačně tedy: 195.50.45.1 bude: 1.45.50.195.in-addr.arpa. Tomuto se reverzní doména.

IPV6 se píše také pozpátku, ale namísto čtveřice hexadecimálních čísel, píšeme jednotlivé znaky po jednom a oddělujeme TEČKOU. Na konci je pak X.X.X.X.X.IP6.arpa. .

Implementace DNS

jmenné servery (server)
resolver (klient) - jedná se o knihovnu, která se volá pro překlad jména na IP
pro komunikace UDP nebo TCP

Pahýlový resolver - ptá se rovnou nejbližšího jmenného serveru
Resolver s Cache pamětí, který si pamatuje předchozí odpověď uživateli

Překlady v DNS z resolveru na jmenný server běží pod UDP

Doména a zóny

Domény mohou být sloučeny do zón, odpovídající nějakému NameServeru. Budu-li mít doménu tvpcom a 10 sub-domén, tak v zóně může být jen 5 těchto sub-domén a dalších 5 využívají zcela jiný NameServer. Tedy tvpcom je autoritativní pro 5 sub-domén v její zóně.

Zóny nám říkají, na jakých NS jsou uložena data o jednotlivých doménách/sub-doménách.


obr. 1: Zonace domén
zdroj: DOSTÁLEK, L. Youtube. Počítačové sítě 11 DNS.[online] [cit. 16-05-2023] Dostupné z: https://www.youtube.com/watch?v=kL7dbKo1UBA&list=TLPQMTYwNTIwMjPbta9ot0k1YQ&index=4

PŘEKLAD domén

Resolvery komunikují s vícero NS, tedy resolver pošle požadavek na překlad nejprve jednomu, pak druhému apod. Jakmile obdrží informaci, tak ostatní odpovědi NS již ignoruje.

NS má jednak CACHE a dále překládá odzadu, tedy zeptá se, kdo je zodpovědný za TLD, doménu 2. stupně atd. až po www.

www.firma.cz

NS se zeptá kořenového NS ("."), kdo je zodpovědný za cz
kořenový NS odpoví IP adresou pro cz
dále se NS zeptá TLD NS, kdo je odpovědný za firma.cz
TLD NS mu vrátí IP adresu takového serveru
firma.cz je již autoritativní, takže vrátí NS ip adresu pro www

Podstatné je, že resolver požádá nejbližší NS a očekává celou odpověď. Zatímco NS se ptají postupně na jednotlivé domény a sub-domény. Resolver žádá rekurzivně - chce celou odpověď. NS žádá jen dílčí odpovědi.


obr. 2: Dotazování DNS
zdroj: DOSTÁLEK, L. Youtube. Počítačové sítě 11 DNS.[online] [cit. 16-05-2023] Dostupné z: https://www.youtube.com/watch?v=kL7dbKo1UBA&list=TLPQMTYwNTIwMjPbta9ot0k1YQ&index=4

Typy DNS serverů

autoritativní - spravují databázi zóny
1. primární - master, administrátor vyplňuje informace o IP
2. sekundární - slave (přebírá informace od master)
3. stealth server - tajný server
ne-autoritativní
1. caching only server (nemá databázi, le pracuje jen s cache)
2. autoritativní server pro jinou zónu

Každý DNS server je primárním jmenným serverem pro loopback. 127.0.0.X -> X.0.0.127.in-adrr.arpa

Ve firmě se klient zeptá místního serveru (používá cache) a ten se iterativně dotazuje jednotlivých NS a poté si odpověď uloží.

RR věty - Resource Records věty

Zde mají NS uloženy informace viz video (odkaz přesměruje rovnou na daný čas, kde se RR řeší). Vždy jsou uloženy v CACHE.

A - a host address
NS - authoritative name server
PTR - DN pointer - umožní překlad IP adresy na doménové jméno
MX - mail exchange - umožní doručit e-mail

[NAME] [TTL] IN typ Data_závislá_na_typu_věty

SOA - věta, která je vždy na začátku konfiguračního souboru zóny: cbu.pvt.cz IN SOA cbu.pvt.cz. bindmaster.cbu.pvt.cz

Dále se zachycuje 5 čísel:

Serial - verze dat
Refresh - interval, jak často sekundární servery ověřují svá data
Retry - interval, kdy sekundární server kontaktuje opakovaně primární server
Expire - limit pro opakované kontaktování primárního serveru
TTL - jak dlouho mohou neautoritativní servery udržovat data z primárního serveru ve své cache

Věta typu A a AAAA (IPV6) nám vrátí IP adresy k jménům.
Věta typu NS definuje autoritativní servery pro danou zónu.
Věta MX specifikuje poštovní server domény, tedy nemusíme psát: xxxx@pocitac.firma.cz, ale jen xxxx@firma.cz.

Postup komunikace a DNS protokol

Primární server po zapnutí načte do CACHE databázi RR vět, kterou má na disku. Sekundární NS si tato data tahají do své CACHE.

HEADER QUESTION ANSWER AUTHORITY ADDITIONAL


obr. 3: Paket protokolu DNS
zdroj: DOSTÁLEK, L. Youtube. Počítačové sítě 11 DNS.[online] [cit. 16-05-2023] Dostupné z: https://www.youtube.com/watch?v=kL7dbKo1UBA&list=TLPQMTYwNTIwMjPbta9ot0k1YQ&index=4

Správa zón

. kdo ví (čína + USA)
TLD (u nás NIC.CZ) - Network Information Centre
dále uživatelé (banka, univerzita, firma...)

Reverzní zóny (poskytování IP adres)

TLD: in-adrr.arpa, IPV6.arpa
Regional Internet address Registry
Poskytovatelé
Uživatelé

DNSSEC

Security extensions, která mají za úkol zabezpečit informace poskytované DNS servery proti spoofingu (podvržení) a proti úmyslné manipulaci.

Resolver může pomocí elektronického podpisu ověřit pravost dat poskytnutých DNS serverem.

Funkce DNSSEC

asymetrické šifrování
držitel domény používající DNSSEC vygeneruje dva klíče (privátní a veřejný)
privátním klíčem podepíše technické údaje, které o své doméně do DNS vkládá
veřejný klíč je držen nadřazenou autoritou - zde je m ožné ověřit pravost údajů držitele domény
u TLD "cz" je veřejný klíč předán nadřazené autoritě - kořenové DNS servery

Zone Signing Key a Key Signing Key

ZSK slouží k podpisu vlastních dat
KSK slouží k podpisu ZSK - tedy vlastně první klíč se opět zašifruje a hash veřejné části klíče je uložen u rodičovské domény
takto se šifrují Resources Records - RRSIG - de facto vytvoříme otisk záznamů a ten zašifrujeme privátním klíčem
autenticita potomka se také ověřuje, a to pomocí Delegation Sign - rodič podepíše veřejný hash potomka

Řetězec důvěry

kořenová doména má veřejný hash klíče na svém webu
RRSIG je validován přes její privátní hash
RRSIG validuje záznam o potomku zahashovaný KSK potomka
takto pokračujeme dále k dalším potomkům až se dostaneme na konec

Útoky

běžný překlad adres nemá žádnou ochranu, tedy může dojít k zneužití názvu (PHISHING) banka.cz a podvržení jiné IP adresy

PHISHING Hacknutí sdíleného webového serveru. Namísto infiltrace jednotlivých webů změní útočník konfiguraci celého serveru a nahraje tam sůj obsah, tedy každá doména - webová stránka - bude mít na pozadí nový falešný obsah.

Zneužití poddomén: www.banka.novefunkce.cz Na první pohled to vypadá, že se přihlašujeme na web banky.cz, ale skutečně se přihlašujeme na web novefunkce.cz

Překlepy v odkazech: www.cs.wikipedia.org/wiki/Domecek

Působí to, jako bychom se měli dostat na web o domečkách, ale jedná se o podvrh s velkým "D", tedy za názvem může být cokoli jiného.

DHCP

Protokol slouží k automatické konfiguraci PC připojených do sítě. DHCP přiděluje pomocí DHCP protokolu jednotlivým zařízením:

ip adresu
masku
implicitní bránu
adresu DNS serveru

Platnost těchto informací je omezená, tudíž na každém počítači běží DHCP klient, který prodlužuje jejich životnost.

Princip DHCP

klient požádá server o IP
server zaznamenává "půjčenou" IP adresu a čas, do kdy ji smí klient používat
po vypršení ji server přiřadí jiným zařízením
klient komunikuje na UDP portu 68, server poslouchá na portu 67
po připojení do sítě broadcastem vyšle klient DHCP paket DHCPDISCOVER
DHCP server odpoví paketem DHCPOFFER s nabídkou IP adres
klient si vybere z nabídky IP adresu a požádá server paketem DHCPREQUEST
server potvrdí DHCPACK paketem - má určitou životnost (klient ji obnoví nebo nesmí IP používat)

Relay agent

Pokud mám více sítí oddělených Routery a jen jedna síť obsahuje DHCP server, tak admin nastaví/zapne na Routeru tzv. relay-agenta. Ten má za úkol broadcastované požadavky ze sítě bez DHCP severu přeposílat do sítě s DHCP serverem. K dotazu relay-agent přidá i číslo sítě a masku, z které klient pochází. DHCP server potom ví, z jakého rozsahu má klientovi adresu přidělit.

Přidělení IP

ručně
statická alokace - DHCP server obsahuje seznam MAC adres a k nim přidělené IP
DHCP vymezí rozsah adres - lease-time IP adresy

SMTP a POP3 a FTP

Simple Mail Transfer Protocol

Klient napíše ve svém poštovním editoru zprávu
Zpráva se uloží na disk do e-mailové fronty
SMTP Client prohlíží onu frontu
SMTP Client se pokouší dopravit zprávu na SMTP server adresáta
Mezi odesílatelem a adresátem může být mnoho "mezilehlých" serverů
Mezilehlé servery uloží zprávu opět do fronty
SMTP klient mezilehlého serveru prohlédne frontu a pošle ji na adresátům SMTP server, tam se vloží do INBOXU (Doručená pošta)
Adresátův editor umí onu zprávu již z INBOXU přečíst

SMTP agent = SMTP client + SMTP server (oboje na jednom serveru)

Každý DNS server má uloženo v Resource Records (např. serverů firmy.cz), kde každý server firmy.cz má svoji prioritu. Čím nižší číslo, tím vyšší priorita a tomu zařízení se to snaží doručit jako k prvnímu.

firmy.cz.	IN MX 10 smtp.firmy.cz.
	IN MX 20 smtp.firmy.cz.
	IN MX 30 smtp.firmy.cz.


obr. 4: SMTP
zdroj: DOSTÁLEK, L. Youtube. Počítačové sítě 12 Mail (SMTP, POP3, MIME).[online] [cit. 16-05-2023] Dostupné z: https://www.youtube.com/watch?v=8tlrsoCs-60&list=TLPQMTYwNTIwMjPbta9ot0k1YQ&index=3


obr. 5: SMTP a POP
zdroj: DOSTÁLEK, L. Youtube. Počítačové sítě 12 Mail (SMTP, POP3, MIME).[online] [cit. 16-05-2023] Dostupné z: https://www.youtube.com/watch?v=8tlrsoCs-60&list=TLPQMTYwNTIwMjPbta9ot0k1YQ&index=3

Protokol POP (Post Office Protocol) slouží k čtení zpráv ze schránky, (může je také rušit či stahovat). SMTP stále slouží k odesílání zpráv na poštovní server a také ke komunikaci mezi servery.

IMAP - Internet Message Access Protocol

Vedle toho existuje také protokol IMAP (dnes IMAP4), který je určen pro vzdálený přístup k e-mailové schránce - prostřednictvím klienta.

Oproti POP3 má pokročilejší funkce - práce se složka mi, přesouvání zpráv mezi složkami, mazání, prohledávání na straně serveru.

S poštovní schránkou pracujeme přes IMAP remotely - tedy veškeré zprávy zůstávají na serveru a do PC se stahují pouze nezbytné informace. Tedy, při zobrazení složky stáhne pouze záhlaví a obsah až když chceme číst.

Rozdíl oproti POP3 je, že POP3 stáhne zprávu zcela, takže ze serveru zmizí a máme ji uloženou lokálně, zatímco IMAP4 ji na serveru ponechá.

U zpráv se uchovává jejich stav - nepřečtená, důležitá, odpověď... .

Protokol umožňuje připojení více klientů zároveň.

VÝHODY IMAP OPROTI POP3

synchronizace - tedy v klientovi i na serveru jsou stejné údaje pro správu, zatímco u POP3 dojde ke stažení zprávy do klienta
připojení je tak dlouhé, jak je dlouhé aktivní spojení, zatímco u POP3 dojde jen ke stažení nových zpráv a spoje ní se přeruší
více klientů připojených současně
zprávy jsou ve formátu MIME (standard pro přenos zpráv v různých kódováních)
práce se složkami/schránkami na serveru - mazání, přesun zpráv mezi nimi apod.
vyhledávání zpráv přímo na serveru

NEVÝHODY

komplikovaný protokol - složitá implementace
prohledávání ve zprávách může značně zatěžovat server

Princip SMTP

Server čeká na portu 25 na požadavky klienta
Klient naváže TCP spojení
Server vrátí hlášku 220 (220 server.firma.cz SMTP a to že je ready)
klient pošle příkaz HELO pc.firma.cz
server pošle odpověď 250 a představí se sám (250 server.firma.cz)
již běží dialog
klient chce na server poslat samotný e-mail
MAIL from (mám mail od tohoto klienta)
server odpoví, že je klient ok / případně SPAM
klient RCPT To (chci to doručit tomuto adresátovi)
server zkontroluje adresáta a řekne adresát ok
když jsou adresáti vyřízeni, tak klient pošle příkaz DATA
server vrátí 354 - dej na poslední řádek tečku
klient pošle zprávu CRLF . CRLF (samostatná tečka na řádku)
server pošle ID zprávy ve frontě a řekne, že zprávu přijal
klient pošle nakonec QUIT a tím se TCP ukončí


obr. 6: ESMTP
zdroj: DOSTÁLEK, L. Youtube. Počítačové sítě 12 Mail (SMTP, POP3, MIME).[online] [cit. 16-05-2023] Dostupné z: https://www.youtube.com/watch?v=8tlrsoCs-60&list=TLPQMTYwNTIwMjPbta9ot0k1YQ&index=3

Počátek je stejný, ale v HELO jsou přehozena písmenka na EHLO. Server pak vrátí více řádků. Max velikost zprávy, způsob autentizace či rozšíření DSN (Delivery Status Notification).


obr. 7: Příkazy POP3
zdroj: DOSTÁLEK, L. Youtube. Počítačové sítě 12 Mail (SMTP, POP3, MIME).[online] [cit. 16-05-2023] Dostupné z: https://www.youtube.com/watch?v=8tlrsoCs-60&list=TLPQMTYwNTIwMjPbta9ot0k1YQ&index=3

FTP

File transfer protocol.

Slouží k přenosu souborů mezi PC a servery po síti. Data lze poslat pomocí browseru, nebo pomocí FTP clienta. Data jsou uložena (většinou na dedikovaných FTP serverech).

FTP protokol je stavový protokol. Uživatel se může autentizovat pro upload dat na server, práva mohou být omezena na určité soubory/adresáře. Autentizační údaje jsou však přenášeny na server v nezašifrované podobě (plane text), což je velké bezpečnostní riziko.

FTP využívá porty TCP/21 a TCP/20. Na 20 se přenáší vlastní data a 21 příkazy.

Přenos může být binární či ascii.

V protokolu je použit model klient-server. Byť režimy jsou aktivní a pasivní. V aktivním režimu navazuje připojení pro přenos dat server a klient poslouchá. V Pasivním režimu navazuje data connection klient.

FTP a SSH

FTP využívá SSH pro tzv. tunelování - SFTP. Problémem může být zajištění bezpečnosti pro obě větve připojení - datové i řídící.

Pro vlastní přenos dat využívá FTP SSH-2, nicméně může běžet i nad jiným protokolem. Právě SSH-2 zajišťuje autentizaci.

SFTP umožňuje:

pokračovat v přerušených přenosech
vypisovat adresáře
odstraňovat soubory na remote PC

Telnet a SSH

Secure Shell je zabezpečený komunikační protokol pro sítě používající TCP/IP. Jedná se o náhradu ze Telnet, rlogin, rsh.

Prostřednictvím SSH posíláme zabezpečená/šifrovaná data skrze síť. Telnet a další posílali data v plane textu.

SSH umožňuje tunelovou výměnu dat (kopírování, přenos) a zabezpečuje autentizaci obou účastníků komunikace, integritu přenášených dat, transparentní šifrování a bezztrátovou kompresi.

Standardně naslouchá SSH na portu TCP/22.

SSH má 3 vrstvy:

transportní - přenášení dat a klíčů, ověření integrity
autentizační - password, public key
spojení

SSH lze narušit metodou man in the middle (Burp Suite). Aby k tomu nedošlo, používá se asymetrická kryptografie.

Dva uživatelé vygenerují private a public keys. Private keys si nechají u sebe (je chráněn heslovou frází). Public key je odeslán na cílový server (uživatelé si jej mezi sebou vymění). Následně server veřejným klíčem zašifruje blok náhodných dat (výzva challenge-response) a pošle ji klientovi, který se snaží na server přihlásit. Pokud klient pomocí svého privátního klíče zprávu dešifruje. Má tímto server ověřeno, že se jedná o klienta se správným klíčem.

Private key neopustí uživatelův počítač a stejně server povolí vstup.

Zdroje

https://www.youtube.com/watch?v=jVuAaBS1t6o&list=TLPQMTYwNTIwMjPbta9ot0k1YQ&index=3
https://www.youtube.com/watch?v=kL7dbKo1UBA&list=TLPQMTYwNTIwMjPbta9ot0k1YQ&index=5
https://cs.wikipedia.org/wiki/Man_in_the_middle
https://cs.wikipedia.org/wiki/Secure_Shell
https://cs.wikipedia.org/wiki/Hypertext_Transfer_Protocol
https://cs.wikipedia.org/wiki/Domain_Name_System

Jaké jsou základní funkce operačního systému?

Popište stručně zavedení operačního sytému u PC. Jak se dělí operační systémy? Uveďte příklady. Pojmy multitasking, monotasking, multiuser, monouser, real time.

Definice OS a jeho zavedení

OS je soubor programových modulů, ve výpočetním zařízení ovládajících řízení prostředků, jimiž je tento výpočetní systém vybaven (procesory, paměti, I/O zařízení a soubory dat). Tyto programové moduly rozhodují spory, dále se snaží optimalizovat výkon, zjednodušit a zefektivnit využívání výpočetního systému.

POST

Před zavedením OS (tedy přímo po spuštění) provádí PC tzv. Power-On Self Test, což je kontrola funkčnosti HW (a dalších esenciální věcí, jako např. integrita BIOS firmwaru). Pokud chybí některá z komponent nebo pokud nefunguje správně, POST to detekuje a pomocí beep codes (série pípnutí) to oznámí uživateli a počítač vypne.

Zavedení OS

z BIOS (Basic Input Output System) - programovatelné paměť nebo UEFI (Unified Extensible Firmware Interface) se zjistí medium, na kterém se OS nachází
na tomto mediu se na MBR (Master Boot Record) načte OS nebo zavaděč OS
- u Linuxů je zavaděčem GRUB a nebo LILO
- jádro /boot/vmlinuz a RAM disk /boot/initrd se zavedou do paměti a převezmou řízení PC

Master boot record

MBR je hlavním spouštěcím záznamem umístěným na pevném disku (na jeho počátku - v prvním sektoru). Velikost MBR je 512 bajtů a obsahuje:

zavaděč OS, kterému BIOS předá řízení PC
- krátký úsek kódu, který je BIOSem zavaden do paměti a spuštěn; úkolem tohoto kódu je načíst do paměti bootovací sektor (v tabulce označen jako aktivní) a spustit ho
tabulku rozdělení disku na logické oddíly
- tabulka obsahuje 4 záznamy včetně informací o zaváděcích sektorech (boot sektory)
číselný identifikátor disku

MBR dokáže adresovat maximálně 2 TB disky.

Bootovaní Red Hat Linux

provede se POST
z BIOS ze zjistí bootovací disk/medium
z MBR se zavede GRUB a načte se jeho konfigurační soubor (/etc/grub/grub.conf)
zavede se jádro (/boot/kernel)
zavede se počáteční RAMka (/boot/initramfs) obsahující potřebné ovladače a následně se připojí kořenový disk systému
spustí se startovací scripty a (/etc/init.d) a zavedou potřebné moduly (/lib/modules)
nastaví se síť, připojí se souborové systémy a připraví se login uživatele

Základní funkce OS

správa a přidělování paměti (zde a zde)
správa procesů - synchronizace
přidělování procesoru - multitasking
řešení Deadlocku
správa systému souborů (virtuální souborový systém)
správa uživatelů

Dělení OS

OS můžeme dělit dle různých kritérií:

Podle správy uživatelů
- monouser (DOS)
- multiuser (UNIX, Windows NT 4.O Terminal Server, MacOS, nebo např. distribuovaný operační systém)
  - více uživatelů pracuje naráz v reálném čase
  - OS musí zajistit rozdělení a oddělení prostředků mezi uživatele
  - OS také dokáže uživatele udržet v bezpečí před vlivy jiných uživatelů (umí je vzájemně oddělit a kontrolovat)
  - existuje zde entita superuživatele (root, administrátor)
Podle počtu spuštěných programů
- monotasking (běží vždy jen jeden program a po jeho ukončení může běžet další; DOS)
- multitasking
Způsoby užití (výkon a odezva)
- Real-Time (v přesných, deterministických systémech)
- Handheld systémy (tablety, mobilní telefony)
  - požadavek na energetickou úsporu
  - zde není kladen vysoký nárok na výpočetní výkon
  - menší display, omezená paměť

Distribuovaný OS

U distribuovaného OS běží software nad sítí propojených zařízení (uzlů). Každý uzel poté běží pod subsystémem globálního OS a HW daného uzlu je řízen tzv. microkernelem. Uzly mezi sebou komunikují a kooperují pod správou speciálních řídících komponent, přičemž celá síť uzlů se navenek chová jako jedno výpočetní zařízení

Real time OS

Více v otázce 3.3 - Architektura OS ve VS a otázce 3.9 Řízení periferií.

V kostce se jedná o OS, které musí pracovat v reálném čase, tedy reagovat na vstupy do přesně stanoveného času (letový provoz, elektrárny, zdravotnictví). Tyto OS se vyznačují tím, že mají většinou jen malé jádro, které ovládá jen základní funkce a na vše další se volají moduly.

FreeRTOS
QNX
RTLinux

Zdroje

PECH, J. Operační systémy 1: Úvod do teorie operačních systémů. České Budějovice: Jihočeská univerzita v Českých Budějovicích, Přírodovědecká fakulta, 2019.
https://cs.wikipedia.org/wiki/Master_boot_record
https://cs.wikipedia.org/wiki/V%C3%ADceu%C5%BEivatelsk%C3%BD_opera%C4%8Dn%C3%AD_syst%C3%A9m
https://cs.wikipedia.org/wiki/Opera%C4%8Dn%C3%AD_syst%C3%A9m#Typy_opera%C4%8Dn%C3%ADch_syst%C3%A9m%C5%AF
https://cw.fel.cvut.cz/b172/_media/courses/a3b33osd/lekce1.pdf
Wikipedia contributors, Power-on self-test [online], Wikipedia, The Free Encyclopedia; 2023 May 13, 07:33 UTC [cited 2023 May 22]. Available from: https://en.wikipedia.org/w/index.php?title=Power-on_self-test&oldid=1154554990.

Metody správy paměti pomocí jedné souvislé oblasti a pomocí sekcí

Metody správy paměti pomocí jedné souvislé oblasti a pomocí sekcí. Pojmy vnitřní a vnější fragmentace paměti.

Mluvíme-li o správě paměti, máme na mysli operační paměť, tedy paměť využívanou procesorem při zpracování instrukcí a dat.

Modul správy paměti má na starost:

sledování stavu každého místa operační paměti
určování strategie přidělování paměti
přidělování paměti úlohám
uvolňování paměti od ukončených úloh
správa virtuální paměti

Přidělování jedné souvislé sekce paměti

Jedná se o nejstarší, ale stále používanou metodu přidělování paměti. Stejně jako u všech dalších metod zde obdrží svou část paměti OS. Zbytek paměti se buď celý, nebo jeho část přidělí právě běžící úloze. Operační systém má tedy na starost jen přidělení paměti úloze, kontrolu, zda úloha nezasahuje do paměti OS a uvolnění paměti po dokončení úlohy.

Je zřejmé, že tato metoda nemůže být použita v systémech vyžadujících multitasking (paměť může být přidělena vždy jen jedné úloze a nebylo by možné mezi úlohami přepínat). Uplatnění však nachází u jednoduchých mikrokontrolérů (používaných např. k jednoduchému řízení spotřebičů), u kterých je vždy vykonávána najednou jen jedna úloha, jako např. ATmega328 (Arduino UNO).


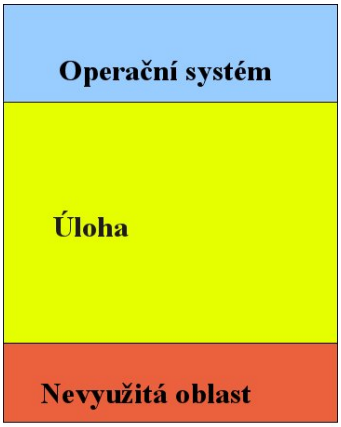obr. 1: Přidělování jedné souvislé sekce paměti
zdroj: PECH, Jiří. Operační systémy 1 - Přidělování paměti. České Budějovice.

Výhody

jednoduchost řešení
rychlost
moznost pracovat i s malou pamětí

Nevýhody

není využita celá paměť
když úloha čeká, není využita ani paměť ani procesor
úlohu nelze vykonat, požaduje-li více paměti, než je k dispozici (neexistuje zde virtuální paměť)

Přidělování paměti po sekcích

Problém absence multitaskingu u předešlé metody se snaží řešit přidělování paměti po sekcích. Zde je paměť rozdělena do sekcí a každá z nich náleží jedné úloze. Tyto sekce mohou být:

všechny stejně velké - statické přidělování
různě velké (podle potřeb úlohy) - dynamické přidělování

Operační systém tedy musí krom výše zmíněných úkolů ještě kontrolovat, odkud kam sahá přidělený prostor úloh (při dalším přidělování) a hlídat, aby si úlohy neovlivňovaly přidělený prostor navzájem.

Tato metoda pochází z 80. let a dnes se v praxi nevyužívá.


obr. 2: Přidělování paměti po sekcích
zdroj: PECH, Jiří. Operační systémy 1 - Přidělování paměti. České Budějovice.

Výhody

umožňuje multitasking
jednoduchá implementace

Nevýhody

z pohledu výkonu poměrně náročná
stále zde neexistuje virtuální paměť)
dochází navíc k vnitřní a vnější fragmentaci

Vnitřní fragmentace

K vnitřní fragmentaci dochází uvnitř alokované oblasti paměti. U statické alokace k ní dochází proto, že každá úloha obdrží stejně velký blok, bez ohledu na to, jestli tolik paměti skutečně potřebuje. U dynamické alokace je důvodem to, že úlohy mají tendenci žádat pro jistotu o větší množství paměti, než reálně potřebují (u přidělování paměti po sekcích totiž není možnost dodatečně přidělit více paměti).


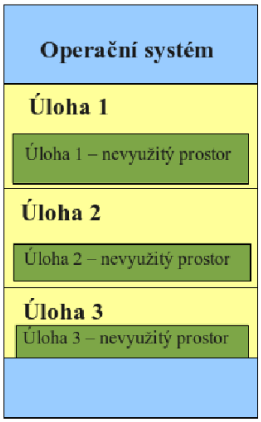obr. 3: Vnitřní fragmentace
zdroj: PECH, Jiří. Operační systémy 1 - Přidělování paměti. České Budějovice.

Vnější fragmentace

K vnější fragmentaci dochází mimo alokovanou oblast paměti. Spočívá v tom, že ač se zdá, že je v systému dostatek paměti pro přidělení nové úloze, správce paměti ji není schopen přidělit, protože tato paměť je rozdělena na více místech a alokace pro novou úlohu se nevejde do žádného z nich.

Nastává, pokud na více místech dojde k uvolnění oblasti paměti (při ukončení úlohy), která se nachází mezi dvěma jinými alokovanými bloky. Řešením je využití metody stránkování (případně dynamické přemisťování sekcí, to je ale technicky a hlavně časově náročné a a také nebezpečné - jsou-li úlohy špatně naprogramovány, mohou se po přemístění snažit přistupovat k paměti na původním místě).


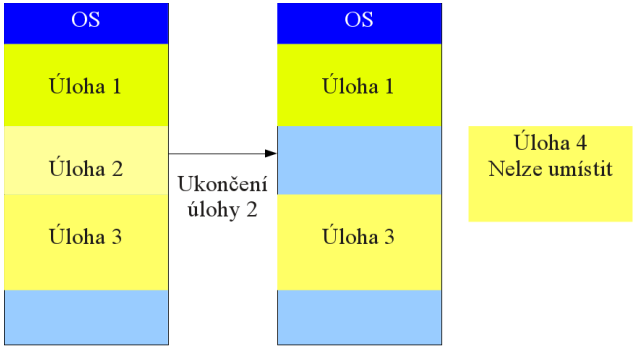obr. 4: Vnější fragmentace
zdroj: PECH, Jiří. Operační systémy 1 - Přidělování paměti. České Budějovice.

Zdroje

PECH, Jiří. Operační systémy 1 - Přidělování paměti. České Budějovice.

Metoda správy paměti pomocí stránkování a stránkování na žádost

Důvodem pro využití stránkování nebo stránkování na žádost (virtuální paměť) je odstranění problému vnitřní a vnější fragmentace (viz kapitola 2.3.2).

Stránkování

Máme paměť, do které chceme zavést aplikaci. Tuto paměť rozdělíme na stránky a naši aplikaci také rozdělíme na stránky o stejné velikosti a poté jednotlivé stránky zavedeme do paměti - stránku na stránku. Tato metoda je hojně užívána.

Výhody

pokud aplikace potřebuje více místa, přidělíme ji další stránku
odstranění vnitřní fragmentace

Nevýhody

musíme udržovat přehled, jaká stránka patří jaké aplikaci
musíme hlídat hranice jednotlivých stránek
pomalá metoda
stále jsme omezeni celkovou velikostí paměti


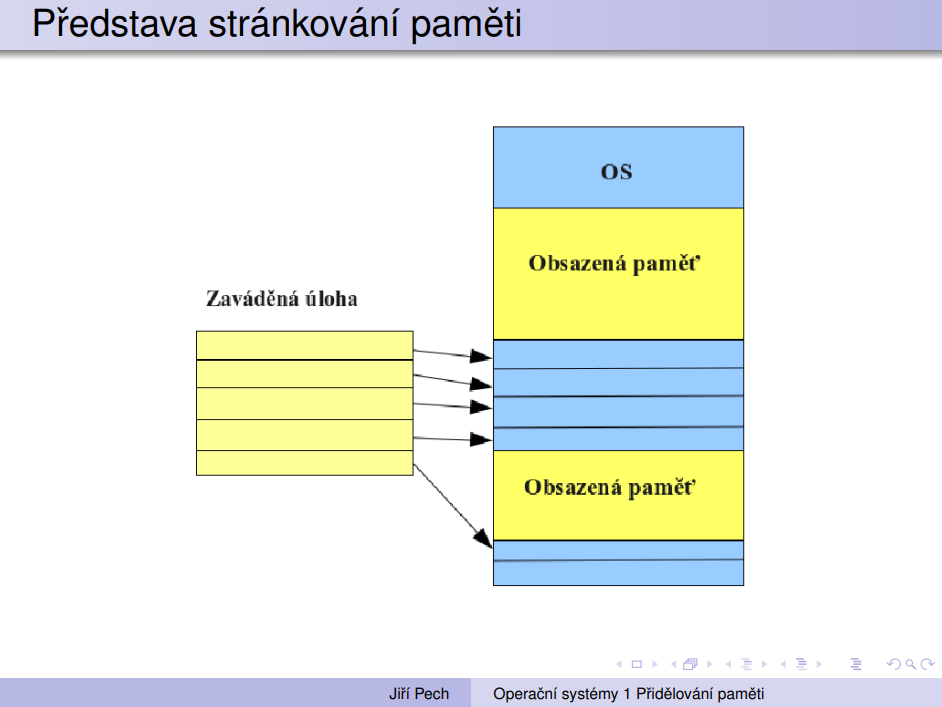obr. 1: Stránkování Dostupné z: https://elearning.jcu.cz/pluginfile.php/343263/mod_resource/content/0/05-Pridelovani_pameti.pdf

Virtuální paměť (Stránkování na žádost)

Vezmeme si úložiště, z něho si sebereme kus a použijeme ho jako nástavec pro paměť RAM. Tuto paměť rozdělíme na stránky. Když chceme přistoupit k paměti na disku, přehodíme požadovanou stránku z disku do operační paměti. Velmi používané v moderních OS.

Výhody

odstranění vnitřní a vnější fragmentace
odpadá omezení velikostí paměti

Nevýhody

přístup k úložišti je pomalejší než přístup k operační paměti (Klidně až 100x pomalejší)
OS si musí udržovat přehled o volných nebo využitých stránkách
nelze zavést virtuální stránku, pokud máme plnou operační paměť (musíme vybrat stránku, která půjde pryč z operační paměti)
- stránka, která byla nejdéle v paměti, jde ven (FIFO)
- Nejčastěji se používá hodinový algoritmus. Pokud je stránka používaná, nastaví se stavový bit stránky na 1. Algoritmus prochází stránky a nastavuje 0, pokud není používaná. Pokud přijde požadavek na přidělení stránky, algoritmus přidělí první stránku, kde nalezne 0.
  - Dnes se používá místo 1 bitu 8 bitů, které se dekrementují o 3. Zabere 3 průchody než se na stránce objeví příznak nuly.

Virtuální paměť se děli na soubor nebo oddíl.

na disku je vyhrazen prostor, který je vyhrazen pro virtuální paměť

Oddíl: Používá se pro Linux nebo MacOS

lze měnit za běhu
pokud máme stránku, kterou budeme jen číst, tak se nezavádí do operační paměti
na MacOS se mění velikost virtuální paměť v závislosti na požadavcích aplikace

Soubor: Používá se na Windows

jedná se o soubor pagefile.sys nacházející se v kořenovém adresáři Windows


obr. 2 Stránkování na žádost Dostupné z: https://elearning.jcu.cz/pluginfile.php/343263/mod_resource/content/0/05-Pridelovani_pameti.pdf

Segmentace

Segmentace spočívá v tom, že část paměti je rozdělena na jednotlivé části, v jedné části jsou knihovny v druhé data, ve třetí programy apod. Aplikace poté sdílí přístup k jednotlivým částem a datům. Nepoužívá se.

Nevýhody

aplikace si navzájem mění data v částech, ke kterým přistupovali

Segmentace se stránkováním

Se segmentací se používá zároveň stránkování. Používalo se ve starších Windows (pro částí, kde je to bezpečné - dynamicky linkované knihovny).

Citace

Fragmentace [online] ©2015 [cit 10.12.2022] Jiří Kysela. Dostupné z: http://fim.uhk.cz/wikiinf/web/index.php/home/6-operani-systemy/409-fragmentace
Operační systémy 1 : Přidělování paměti [online] ©2019 [cit 10.12.2022] Jiří Pech. Dostupné z: https://elearning.jcu.cz/pluginfile.php/343263/mod_resource/content/0/05-Pridelovani_pameti.pdf

Stavový diagram procesů

Jednotlivé stavy. Pojem multitaskingu a jeho druhy. Správa procesů v reálných OS.

Proces

Proces je instancí aplikace/programu uvnitř OS. Uživatel spustí appku a ta si po svém spuštění vytvoří proces.

Jedná se o základní jednotku práce OS.

V rámci OS běží současně jednak procesy appek a jednak procesy OS. Každý z procesů si může pustit další procesy, těm následně říkáme synovské. Jsou tedy 2 druhy procesů:

rodičovské
synovské

Synovský zaniká se zánikem rodičovského procesu.

Každý proces je reprezentován záznamem v paměti - Process Control Block (PCB) obsahujícím informace o procesu:

status procesu
program counter
CPU registry
CPU plánovaní - priorita procesu
info správy paměti
info o času přidělení CPU, časový limit, číslo procesu
I/O stavové informace


obr. 1: Stavový diagram procesu
zdroj: PECH, J. Operační systémy 1: Procesy. České Budějovice: Jihočeská univerzita v Českých Budějovicích, Přírodovědecká fakulta, 2019.

Popis diagramu

Nový - proces je zaveden a vzniká jeho PCB
Připraven - proces je v operační paměti
- OS vybere proces ke zpracování
Probíhající - pokud jej OS vybral pro zpracování
- zde se proces nachází na CPU a běží
Ukončen - proces končí
Čekající - proces čeká na I/O událost, pro ukončení I/O události se opět proces dostane do stádia čekající (I/O zde může být čtení z klávesnice, čtení z disku, tisk na tiskárně)

Pokud je procesu odejmut čas na CPU, tak se proces přeruší a rovněž se vrací do stádia Připraven.

Přidělení CPU

Slouží k tomu dva moduly:

CPU Scheduler - vybere vhodný proces pro spuštění
Dispatcher - zavede proces na CPU
- přepnutí kontextu - uvolnění procesu z CPU a uložení důležitých informací (stav registru, následující instrukce ke zpracování, stack...) a zavedení nového procesu na CPU (zde info o stacku, registrech a následující zpracovávané instrukci nahráváme)

Čas, který má proces na CPU přidělen se nazývá časové kvantum.

Metody výběru procesu ke zpracování:

FIFO
First Come First Served - úlohy, které je třeba spravovat opakovaně nemusí dostat potřebný čas na CPU
Short Job First - úlohy s dlouhým během se moc nedostanou k CPU
Prioritní fronta - tasky s nízkou prioritou se nemusí na CPU vůbec dostat; tomuto se zamezuje tím, že po určitém počtu cyklů se zvýší priorita daného procesu, takže se časem na CPU zkrátka dostane

Priority v Reálných OS

Linux - priority od -19 (nejvyšší) do 20 (nejnižší)

Defaultní priorita je 0. Uživatel může prioritu snížit, ale nemá oprávnění ji navyšovat.

Windows - 0 až 31 (nejvyšší)

Systémové procesy mají vždy vyšší prioritu, než procesy uživatelské.

Priority je možné nastavit staticky - tj. při spuštění, nebo dynamicky, kdy se mění za běhu.

Multitasking

Střídání procesů na procesoru a současné spouštění vícera procesů.

Rozlišujeme:

Preemptivní multitasking - zaručuje pravidelné střídání
- pokud proces neodejde do určité doby do stavu Přerušen nebo Ukončen, tak je mu CPU odebrán a dojde k přepnutí kontextu
Nepreemptivní multitasking - nemáme zaručeno pravidelné střídání procesů na CPU
- pseudomultitasking - MS-DOS
  - MD-DOS je sice monotaskový OS, ale například při tisku na tiskárně; uživatel jinak procesu přepínat nemůže
- kooperativní multitasking
  - procesor sám předává proces
  - externí program přepíná appky na CPU (program Finder na MacOS 8 a 9)
  - procesy přepíná sám uživatel

Procesy a vlákna

V moderních OS se procesy dělí na vlákna a při přidělování vláken mluvíme o přidělování nikoli na CPU, ale na jádro CPU. Rozdíl mezi procesem a vláknem je dobře představitelný na Browseru a jeho záložkách. Browser je proces a jeho záložky jsou jednotlivá vlákna.

Vlákna se mohou nacházet ve stavu: připraveno, blokováno, spuštěno či ukončeno. Dále mohou vytvářet synovská vlákna.

Vlákna jsou na sobě (na rozdíl od procesu) závislá. Všechna vlákna mají přístup na libovolnou adresu úlohy. Jedno vlákno může číst nebo zapisovat do libovolného zásobníku jiného vlákna téže úlohy. Ochrana paměti mezi vlákny není zapotřebí. Vlákna jsou naprogramována tak, aby si navzájem pomáhala.

Životní cyklus procesu v reálném OS - Linux


obr. 2: Životní cyklus procesu na Linuxu
zdroj: PECH, J. Operační systémy 1: Procesy. České Budějovice: Jihočeská univerzita v Českých Budějovicích, Přírodovědecká fakulta, 2019.

Rozdíly oproti původnímu obrázku:

Běh jádra leží zcela mimo cyklus, a to proto, že procesu jádra mají absolutní přednost před všemi ostatními.

Stavy Čeká, Čeká na disku a Připraven na disku jsou stavy, kde je proces odložen na disk (mimo RAM).

Zombie - je-li proces ukončen na CPU, tak se nejprve dostane do stavu ZOMBIE, zde může ještě zůstat, pokud má spuštěny synovské procesy. Z tohoto stavu může být proces již jen ukončen, nemůže se vrátit do žádného jiného stavu.

ZDROJE

PECH, J. Operační systémy 1: Procesy. České Budějovice: Jihočeská univerzita v Českých Budějovicích, Přírodovědecká fakulta, 2019.

Vysvětlete pojmy synchronizace procesů a kritická sekce

Synchronizace procesů je způsob řízení procesů tak, aby žádné dva procesy nepřistupovali zároveň ke stejným datům. Většinou se nesynchronizují procesy, ale vlákna.

Je nutné synchronizovat zejména paralelní procesy z důvodu tzv. Časově závislé chyby

Časové závislá chyba: vzniká podle pořadí přístupu procesu k proměnné.
- Jeden proces načte hodnotu 10 000 a přičte k ní 5000, druhý od 10 000 odečte hodnotu 5000. Jeden proces zapíše hodnotu 15 000, ale druhý ji ihned přepíše hodnotou 5000.

Lze řešit pomocí Bernsteinových podmínek: pokud proces zapisuje do paměti, jiný proces nesmí do této paměti přistupovat.

Kritická sekce

Kritická sekce je část kódu, kterou nelze sdílet. Je třeba zajistit následující:

Vzájemné vyloučení: do kritické sekce smí přistupovat pouze jeden proces, který bude zapisovat
Dostupnost kritické sekce: proces musí mít možnost se k ní v přiměřeném čase dostat. (Pouze ty procesy, které při uvolněn kritické sekce byly přítomny u čekání mohou rozhodovat, který přistoupí další. Toto rozhodování musí skončit v konečném čase. Zabraňuje vzniku blokování, nebo deadlocku)
Konečné čekání: pokud chce proces přistoupit do kritické sekce, musí na něj přijít řada v konečném čase. (Ostatní procesy "předbíhají" čekající proces a neumožní mu vstoupit. Musí tedy existovat nějaké počítadlo, určující kolikrát mohou jiné procesy vstoupit do kritické sekce, než je vynucen přístup čekající procesu.) Zabraňuje vzniku stárnutí)
Proces je v kritické sekci konečnou dobu. Správně naprogramovaný proces je v kritické sekci pouze po nezbytně nutnou dobu.

Řešené problémy

Deadlock – uváznutí, procesy ze vzájemně zablokují
Blokování – proces do kritické sekce nemůže, i když je volná. Zbytečné čekání na uvolnění kritické sekce.
Stárnutí – jeden proces čeká nemožně dlouho na povolení k přístupu do kritické sekce

Algoritmy pro přístup do kritické sekce:

Petersonův algoritmus: proces se zeptá, zdali nějaký proces nechce do kritické sekce a pokud ano, pustí ho.
Bakery algoritmus: FIFO, fronta. Procesy se zařadí za sebe a postupně přistupují do kritické sekce.
Hardwarové řešení: funkce TestAndSet. Režie je v rámci procesoru, tato režie je poměrně vysoká a nelze ji tedy použít jako stálé řešení přístupu do kritické sekce.
Semafor: celočíselná proměnná, udávající přístup do kritické sekce. Má tři možné stavy: kladnou hodnotu, nulu a zápornou hodnotu. Záporné číslo udává, kolik procesů smí do kritické sekce. Nula říká, že kritická sekce je obsazená a kladná hodnota říká, že kritická sekce je obsazená a kolik procesů čeká ve frontě. Jedná se o vylepšenou frontu. Pokud proces opustí kritickou sekci, semafor sníží hodnotu o 1. Jakýkoliv přístup k semaforu musí být hlídaný, aby se dva procesy nekoukly zároveň, nezjistili že je volno a nevstoupili do kritické sekce. Na toto se používá funkce TestAndSet. Je nutné hlídat jak zápis, tak čtení.
Mutex (Binární semafor): Jedná se o zjednodušený semafor, který nabývá pouze stavů 0 a 1. Pokud je stav 0, proces může přistoupit do kritické sekce a změnit hodnotu na 1. Dokud je hodnota 1, žádný další proces do ní nemůže. Po opuštění kritické sekce proces nastaví stav na 0.
Monitor: Přístup outsourcujem a zavádíme separátní program, který se stará o přístup do kritické sekce.

Citace

Synchronizace procesů. [online] @2018 [cit 7.12.2022] Jiří Pech. Dostupné z: https://elearning.jcu.cz/pluginfile.php/347352/mod_resource/content/0/Synchronizace_procesu.pdf
Introduction of Process Synchronization. [online] @2022 [cit 7.12.2022] GeekForGeeks. Dostupné z: https://www.geeksforgeeks.org/introduction-of-process-synchronization/

Deadlock

Pojmy : Deadlock. Vysvětlete příčiny deadlocku. Jak lze deadlocku zamezit. Jak je řešen deadlock v reálných OS.

Deadlock je v OS čekání na událost, která nemůže nastat, neboli situace, kdy úspěšné dokončení první akce je podmíněno předchozím dokončením druhé akce, přičemž druhá akce může být dokončena až po dokončení první akce.

Příkladem deadlocku mohou být dva procesy, kde každý drží otevřený soubor a potřebuje zapsat do souboru druhého procesu. Dalším příkladem může být dopravní situace (viz obr. 1).


obr. 1: Příklad Deadlocku (v dopravní situaci)

Podmínky vzniku deadlocku

K uváznutí dojde jen při splnění všech následujících podmínek:

Vzájemné vyloučení - každý nesdílitelný zdroj může v jednom okamžiku používat nejvýše jeden proces (aby nedošlo k porušení konzistence dat) jen jeden proces
Drž a čekej - proces může žádat o další zdroje, i když už má nějaké přiděleny
Nepreemptivnost - jakmile proces zmíněný zdroj vlastní, nelze mu ho odejmout, musí ho sám vrátit
Kruhové čekání - procesy čekající vzájemně na zdroje

Nesdílitelné zdroje jsou zdroje, které nemohou sdílet dva procesy najednou (např. tiskárna nebo soubor pro zápis). Sekvence užití zdrojů:

Dotaz na dostupnost zdroje - nelze-li dotaz vyplnit okamžitě, musí proces čekat
Užití - proces pracuje se zdrojem
Uvolnění zdroje

Dotaz a uvolnění jsou kritická sekce. Pokud nemůže proces dostat zdroj - čeká. Pokud čekají nejméně dva procesy na zdroj, který drží jiný čekající proces máme deadlock.

Metody řešení deadlocku

Prevence deadlocku
- Zrušení některé podmínky deadlocku:
  - Nepoužívat zámky u prostředků umožňujících sdílený přístup
  - Proces může žádat o další prostředky až tehdy když všechny své uvolnil
  - Pokud proces požádá o nedostupný prostředek je pozastaven, jsou mu všechny prostředky odebrány a čeká se až může všechny prostředky obdržet
  - Prostředky mají stanovené pořadí a Ize je získat pouze v tomto pořadí
Vyhýbání se deadlocku
- Každý proces před začátkem oznámí kolik bude potřebovat prostředků. Nelze jej spustit pokud existuje možnost, že mu prostředky nebudou moci být zajištěny
  (příkladem je tzv. Bankéřův algoritmus - bankéř nemůže půjčit, pokud nemůže zajistit požadavky na výběr všech vkladů)
Detekce deadlocku a zotavení po uváznutí
- Vychází z předpokladu, že je deadlock nepravděpodobný. Systém se snaží cyklicky detekovat deadlock a řešit ho. Možné způsoby jsou:
  - Ukončení procesu (restart procesu)
  - Odebraní zdroje nějakému procesu
Ponecháaní řešení deadlocku na lidské obsluze
- Postupné ukončování procesu a sledování, zda se systém rozběhne
- Restart systému (může dojít ke ztrátě dat a opětovnému deadlocku)

Body 1 až 3 jsou složité a náročné na zdroje, proto je běžné operační systémy používají pouze okrajově a většinou nechávají řešení deadlocku na obsluze.

Citace

Wikipedie: Otevřená encyklopedie: Deadlock [online]. c2022 [citováno 22. 01. 2023]. Dostupný z WWW: https://cs.wikipedia.org/w/index.php?title=Deadlock&oldid=22253321

Pojmy adresářová struktura, soubor, souborové systémy

Pojmy adresářová struktura, soubor, souborové systémy. Metody plánování disku. Ochrana souborů a adresářů v reálných OS.

Adresářová struktura

Je organizační struktura souborového systému. Adresáře slouží k seskupování souborů a další adresářů. Z pohledu OS je adresář jen speciální soubor, který obsahuje informace o adresářích a souborech v něm obsažených. Nejvyšší adresář se nazývá kořen (root) (v UNIXech /, u Windows má každý oddíl vlastní root, např. C:\).

Složka vs adresář

adresář (directory)
- označuje skutečný prvek souborového systému
- např. /bin/bash
složka (folder)
- abstrakce používaná v grafickém rozhraní
- nemusí označovat jen adresář, ale i např. tiskárnu či ovládací panely ve Windows
- cílem je zjednodušení a unifikace přístupu uživatele k různým prvkům

Zjednodušeně, adresář se tomu říká z pohledu FS, složka z pohledu grafického rozhraní.

Druhy adresářových struktur

jednoúrovňová
- existuje pouze adresář root a vše jev něm
- nejstarší metoda
- příklad OS: CP/M
dvouúrovňová
- v rootu jsou adresáře, ale ty už mohou obsahovat jen soubory
- příklad OS: RSX
stromová
- v každém adresáři mohou byt další soubory i adresáře
- příklad OS: FAT
acyklická
- organizace je rovněž stromová
- soubory a adresáře mohou být ve více adresářích (pomocí odkazů (linků))
- nesmí dojít k cyklení (dva adresáře se nemohou odkazovat navzájem)
- nejpoužívanější
- příklad OS: NTFS, Ext
cyklická
- může obsahovat cykly

Soubor

Soubor je základní jednotkou pro ukládání dat v rámci souborového systému. Jedná se o označenou (pojmenovanou) množinu dat uloženou na paměťovém médiu, se kterou může OS pracovat. Formát dat v souboru je definován typem souboru. Ten lze rozpoznat následujícími způsoby:

podle hlavičky
- prvních několik bytů souboru
- je to jednoznačné
- trochu pomalejší (musí se projít tabulka známých formátů)
- používá se UNIXových systémech
podle přípony
- např .jpg
- přípona není jednoznačná, lze ji jednoduše změnit a BFU poté soubor neotevře
- používá se ve Windows
podle metadat
- ta jsou uložena mimo soubor
- spravuje to souborový systém
- při přenosu mezi systémy se musí konvertovat
- existují různé varianty, nejběžnější je MIME type, který se používá hlavně na internetu (např. application/json, text/html)

Soubory můžeme kategorizovat podle různých hledisek, např.:

kolik souborů ve skutečnosti obsahuje
- jednoduchý - jen jeden soubor (obyčejný textový dokument, obrázek, atd.)
- složený - obsahuje více souborů (archivy (.zip, .tar.gz), multimédia (video + titulky), atd.)
podle typu obsahu
- textový - prostý text, HTML, MD, atd.
- binární - aplikace, obrázky, audio, atd.
podle účelu z pohledu OS
- standardní - klasické soubory
- adresáře - viz výše
- simulované - reprezentují I/O zařízení
- odkládací - SWAP
podle přístupu k médiu
- přímý - můžeme přistoupit na kterýkoliv soubor kdykoliv (např. pevný disk, CD)
- sekvenční - musíme projet celé médium od aktuálního místa až na požadované (např. magnetická páska)
- indexový - lze přecházet přímo na vybraná místa - indexy (např. magnetická páska s přeskakováním)

OS zajišťuje nad souborem následující operace:

vytvoření
čtení
zápis
vyhledání/změna místa v souboru (odkud čteme, kam zapisujeme)
smazání

Fragmentace

Podobně jako u primární paměti, dochází k fragmentaci i u sekundární. Máme opět dva druhy:

vnitřní - malé soubory nezabírají celý cluster, ve kterém potom zbývá nevyužité místo
vnější - jednotlivé clustery, ze kterých se soubor skládá jsou rozmístěny po celém disku (jejich čtení trvá dlouho)

Souborové systémy

Souborový systém je způsob organizace dat na paměťovém médiu. Určuje jejich strukturu a další vlastnosti, které ovlivňují to, jak se s nimi pracuje.

Jednou z důležitých vlastností souborových systémů jsou způsoby zápisu dat na úložiště. Ty jsou následující:

okamžitý zápis
- zápis probíhá ihned po zadání požadavku
- v daném okamžiku probíhá jen jedna operace zápisu
- nedojde ke ztrátě dat, ale je to pomalé
- např. FAT
opožděný zápis
- data se nejprve zapisují do cache paměti a poté postupně na trvalé místo (až když není systém zaneprázdněn)
- rychlejší, ale při výpadku může dojít ke ztrátě dat (těch co byla zatím pouze v cache)
opatrný zápis
- používají se transakce (jako u DB)
žurnálovací systémy
- uchovávají se informace (metadata) o provedených operacích
- při výpadku je možné data obnovit
- doplňuje opožděný zápis
- tvorba žurnálu zpomaluje souborový systém (cca o 30%)
- např. EXT4, NTFS

Související pojmy:

RAID (Redundant Arrays of Inexpensive/Independent Disks)
- použití více disků dohromady
- verze (jen ty nejpoužívanější):
  - RAID 0 (stripping) - zápis na více disků najednou - vyšší rychlost
  - RAID 1 (mirroring) - stejná data na více discích - vyšší bezpečnost
  - RAID 5 - data se zapisují na více disků a jeden se používá k ukládání kontrolních součtů (přijdeme-li o nějaký disk, jeho obsah se po náhradě dopočítá z kontrolních součtů) - vyšší rychlost i bezpečnost
  - RAID 6 - pro kontrolní součty se používá více disků (každý může mít jinou metodu tvorby kontrolních součtů)
- můžeme mít HW (dedikované HW zařízení v PC - je rychlejší) a SW (stará se o něj OS - v případě problému s OS můžeme přijít o data) RAID
síťové souborové systémy
- spojování více úložišť z fyzicky oddělených PC do jednoho FS (něco jako RAID)
- Ceph, GlusterFS
VFS (Virtual File System) - definice operací, které musí zvládnout každý souborový systém bez ohledu na skutečné HW umístění (nezáleží na tom, na jakém zařízení se nachází); cílem je uniformita
LVM (Logical Volume Manager) - kombinování fyzických disků pomocí logických (které potom můžeme upravovat podle potřeby)

FAT

nejstarší dosud používaný systém (od MS-DOS)
na začátku disku se nachází FAT (File Allocation Table), ve které se nacházejí informace o souborech
FAT se snadno prohledává → systém je velmi rychlý
pokud dojde k poškození FAT, znamená to ztrátu všech dat (ve skutečnosti je lze obnovit pomocí různých nástrojů); aby se tomu předešlo, obsahují nové verze FAT tabulky dvě, na různých místech disku
nepoužívá žurnálování
používá se tam, kde je potřeba spíše rychlost než spolehlivost → paměťové karty, flash disky
verze (chronologicky): FAT12, FAT16, VFAT (Virtual FAT), FAT32, exFAT (Extended FAT)
omezení:
- v rootu (kořenovém adresáři) může být maximálně 255 souborů
- maximální velikost souboru je $ 2^n $ bytů, kde $ n $ odpovídá číslu v názvu verze, tedy např. 32 pro FAT32
- maximální velikost oddílu (ve Windows) 32 GB
- původně maximální délka názvu souboru 8 znaků + 3 přípona (s VFAT došlo k prodloužení)
- používá stromovou strukturu, kvůli které nepodporuje odkazy
- neumožňuje přidávat k souborům a adresářům přístupová práva (pouze lze soubor označit jako read-only)

NTFS

New Technology File System
poprvé u Windows NT (dnes prakticky na všech strojích s Windows)
proprietární
používá žurnálování
názvy používají Unicode (lze použít jiné znaky než ASCII)
umožňuje nastavení práv
má indexování souborů (= rychlé vyhledávání)
umožňuje odkazy (i pevné (vydrží i po přemístění původního souboru))
lze jej šifrovat
efektivně ukládá soubory, které obsahují převážně 0 (řídké soubory)
vyhledává, opravuje a případně blokuje vadné sektory za běhu

EXT (Extended)

používá se v UNIXových systémech
disk se dělí na bloky (o velikosti 512, 1024, 2048 nebo 4096 B)
- první je boot block (na systémovém disku obsahuje zavaděč, jinde je nevyužit)
- další se dělí do skupin, z nichž každá obsahuje superblock s informacemi o celém disku (při poškození superblocku se může použít jiný)
podporuje odkazy
- soft link - odkazuje na místo (jako zástupce na Windows)
- hard link
  - odkazuje přímo na soubor
  - cíl ten nelze smazat, dokud existuje hard link
  - nesmí se zacyklit
  - nemůže odkazovat na jiný disky a sám na sebe
informace o souboru jsou obsaženy v tzv. i-node (uzlech)
volný prostor je evidován v řetězovém seznamu
verze:
- Ext - již se nepoužívá
- Ext2
  - nemá žurnálování
  - používá se u zaváděcích oddílů UNIXových systémů (lze i tam, kde FAT)
  - maximální velikost souboru je 12 TB
  - maximální velikost oddílu je 16 TB
- Ext3 - již se nepoužívá (je jako Ext4, ale má více omezení velikosti)
- Ext4
  - používá se jako hlavní FS pro Linux
  - maximální velikost souboru je 16 TB
  - maximální velikost oddílu je 1 EB

XFS

od IBM
je 64 bitový
používá se v rozsáhlých UNIXových úložištích
žurnálují se jen metadata (rychlejší a méně bezpečné než klasické žurnálování souborů)

ZFS

Zetabyte File System
původně od SUN (pro OS Solaris)
licence blokuje použití v Linuxu
je 128 bitový
umí automaticky opravovat chyby

btrfs

B-tree File System
podobný ZFS
vznikl kvůli licenčním problémům ZFS
obsah adresářů má strukturu B-stromů
začíná být v Linuxu populární (např. Fedora jej využívá jako hlavní FS)

APFS

Apple File System
pro MacOS
nahradil starší HFS

ISO 9660

pro CD, DVD a BR
délka souboru maximálně 32 znaků
maximální hloubka adresářové struktury je 7 úrovní
existují rozšíření:
- Joliet - dlouhá jména pro Windows
- Rock Ridge - totéž pro UNIXy
- El Torito - umožňuje boot

Metody plánování disku

Je činnost, která nám říká, jakým způsobem dochází k vyřizování požadavků na čtení a zápis, aby byly minimalizovány zbytečné pohyby čtecí hlavy, otáčení ploten a prodleva mezi požadavky (týká se tedy jen HDD).

Metody:

FCFS (First-Come First-Served)
- požadavky jsou vyřizovány v pořadí, v jakém došly (tedy FIFO)
- může docházet k větším prodlevám, pokud jsou požadované oblasti daleko od sebe
SSTF (Shortest-Seek-Time-First)
- nejprve se vyřídí ten požadavek, který vyvolá nejmenší posun hlavy
- hrozí zastarání vzdálenějších požadavků
SCAN plánování
- hlava projíždí disk tam a zpět z jednoho konce na druhy a cestou vyřizuje požadavky (tzv. Elevator algoritmus)
C-SCAN
- ještě lepší než SCAN
- hlava se po dojeti na konec disku vrátí na začátek, jako by začátek navazoval na konec
- možné vylepšení: pokud už dále není žádný požadavek, vrací se rovnou (bez dojetí na konec), a to na místo prvního požadavku (ne na začátek)

Ochrana souborů a adresářů v reálných OS

Linux

systém oprávnění z UNIXu
neřeší se dědění (kromě práva vstupu do adresáře)
velmi jednoduché
každý soubor (adresář) má tři kategorie oprávnění:
- vlastník
- skupina
- ostatní
každá z těchto kategorií se skládá z následujících práv (každému z práv náleží jedno oktální číslo):
- čtení - r (4)
- zápis - w (2)
- spuštění souboru/vstup do adresáře - x (1)
celková oprávnění pro každý soubor (adresář) se skládají ze tří oktálních čísel, která odpovídají součtu práv pro každou kategorii
příkladem může být: 764, což znamená, že vlastník může vše (4 + 2 + 1), příslušník skupiny souboru může číst a zapisovat (4 + 2) a ostatní mohou jen číst (4)
často se používá rozložený zápis (např. při použití ls -l), který pro předešlý příklad vypadá takto: -rwxrw-r-- (první pomlčka neznamená oprávnění, ale typ souboru: - obyčejný soubor, d adresář, l linka, b blokové zařízení, c znakové zařízení, p roura, s soket)
pokud uživatel spadá do více kategorií, bere se v potaz vždy ta nejkonkrétnější kategorie, tedy ta nejvíce vlevo (v oktálních číslech)
vždy je nutné, aby uživatel měl právo na vstup ke všem nadřazeným adresářům
k editaci oprávnění se používá příkaz chmod, např.: sudo chmod a+x soubor.sh přidá (+) právo spouštět soubor (x) všem třem kategoriím (a)

Windows

oprávnění lze přidělit nejen souborům a adresářům, ale i objektům registrů, systémovým objektům nebo Active Directory objektům
oprávnění lze přidělit:
- skupinám, uživatelům a dalším objektům s identifikátory zabezpečení v doméně
- skupinám a uživatelům v této doméně a ve všech důvěryhodných doménách
- místním skupinám a uživatelům (v počítači, kde se objekt nachází)
lze přidělit tato oprávnění:
- full control - umožňuje dělat prakticky vše (včetně úpravy oprávnění a přebírání vlastnictví)
- modify - umožňuje všechny úpravy a samozřejmě čtení (vytvářet, editovat a mazat soubory, vytvářet a mazat adresáře)
- read & execute - čtení (jak dat souborů, tak obsahu adresářů) a spouštění aplikací
- list folder contents - čtení obsahu adresářů a podadresářů (ne souborů)
- read - jako list folder contents + obsah souborů
- write - jako read + tvorba adresářů a souborů a mazání souborů
vlastník souboru (adresáře) může bez ohledu na oprávnění vše
je možno oprávnění dědit, tedy soubory a podadresáře dostávají oprávnění od svého předka

macOS

používá UNIXová oprávnění, stejně jako Linux

ACL

Access Control List
tabulka se záznamy o oprávněních ke každému souboru (adresáři)
umožňuje jemnější nastavení oprávnění (každý záznam v ACL se váže ke konkrétnímu uživateli/skupině)
lze je použít jak ve Windows, tak UNIXových systémech (nejsem si jistý, ale Windows je možná užívají ve výchozím stavu - nebo je jejich model dost podobný)

Zdroje

PECH, Jíří. Operační systémy: Elektronická skripta. České Budějovice, 2012. ISBN 978-80-7394-384-4.
PECH, Jiří. Operační systémy 1 - Souborové systémy. České Budějovice.
Přispěvatelé Wikipedie, File Allocation Table [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 2. 02. 2023, 15:38 UTC, [citováno 8. 05. 2023] https://cs.wikipedia.org/w/index.php?title=File_Allocation_Table&oldid=22404578
Přispěvatelé Wikipedie, Btrfs [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 2. 08. 2022, 14:42 UTC, [citováno 8. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Btrfs&oldid=21550356
Přispěvatelé Wikipedie, Soubor [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 9. 11. 2022, 10:08 UTC, [citováno 9. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Soubor&oldid=21860541
Přispěvatelé Wikipedie, Formát souboru [online], Wikipedie: Otevřená encyklopedie, c2021, Datum poslední revize 14. 05. 2021, 01:58 UTC, [citováno 9. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Form%C3%A1t_souboru&oldid=19844688
Přispěvatelé Wikipedie, Adresář (informatika) [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 9. 11. 2022, 09:44 UTC, [citováno 9. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Adres%C3%A1%C5%99_(informatika)&oldid=21860455
https://www.pslib.cz/milan.kerslager/P%C5%99%C3%ADstupov%C3%A1_pr%C3%A1va_v_Linuxu
https://learn.microsoft.com/en-us/windows/security/identity-protection/access-control/access-control
https://www.uwec.edu/kb/article/drives-establishing-windows-file-and-folder-level-permissions/
https://www.imperva.com/learn/data-security/access-control-list-acl/
Přispěvatelé Wikipedie, Access Control List [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 7. 02. 2022, 07:57 UTC, [citováno 9. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Access_Control_List&oldid=20912840

Syntaxe a sémantika programovacího jazyka

Pojem proměnná, její deklarace a inicializace. Rozsah platnosti proměnných (lokální, statické). Syntaktická kategorie příkaz a výraz v programovacím jazyce

Syntaxe vs Sématika

Syntaxe je správnost gramatiky -> správnost napsaných slov, v programovacím jazyce příkazů a výrazů. Syntaxe se kontroluje syntaktickým analyzátorem.
Sématika je význam jednotlivých slov -> v programovacím jazyce význam příkazů nebo výrazů.

Proměnná

Proměnná je odkaz na hodnotu. Tato hodnota je uložená v paměti. Skrze proměnnou k této hodnotě přistupujeme.

V programování můžeme zápis proměnné rozdělit na deklaraci a inicializaci.

Deklarace

Jedná se o vytvoření odkazu do paměti, kde paměť ještě nenese žádnou hodnotu. Deklarace vytvoří proměnnou, ale hodnotu této proměnné přiřadíme až pomocí inicializace.

int number; // Deklarace primitivní proměnné typu int
Car car; // Deklarace objektové proměnné typu Car

Inicializace

Inicializací přiřadíme do paměťového místa, na které proměnná odkazuje, hodnotu. Tedy, přiřazujeme proměnné hodnotu. Můžeme to udělat ihned při deklaraci, nebo až později.

int number = 5; // Deklarace s inicializací
Car car; // Deklarace objektové proměnné typu Car
car = new Car(); // inicializace po deklaraci

Rozsah platnosti proměnných

Rozsah platnosti nám určuje, v jakých částech kódu můžeme k proměnné přistupovat vzhledem k tomu, kde byla vytvořena

Obecně platí, že pokud deklarujeme proměnnou v určitém bloků kódu, tak lze k této proměnné přistupovat pouze v tomto bloku a ve vnořených blocích.

while (a > 6){
   int value = a;
}

System.out.println(value); // Tady k proměnné již přistupit nelze. Není zde vidět. Paměť, která se vztahovala jak k referenci (jméno proměnná), tak k inicializované hodnotě již byla uvolměna.

Lokální proměnná

Jedná se o proměnnou, která je deklarována v rámci určitého bloku, funkce. Je tedy lokální, stejně jako na vesničce (bloku) je lokální jednota. Lidi ve vesničce o ni ví, ale ve vesnici vedle, nedej bože městě už nikdo netuší, že tam něco takového je.

Lokální proměnná je příklad výše. Je nepřístupná vně bloku. Lokální proměnná se značí private.

Statická proměnná

Tato proměnná náleží třídě. To znamená, že nezávisle na instanci třídy (objektu té samé třídy) se jedná o přístup do stejné paměti.

class People(){
   public static int peopleCount = 0;

   public People(){
       peopleCount++;
   }


}


class main{

   public static void main[String[] args]{
       People somePeople = new People(); 
       System.out.println(somePeople.peopleCount) // výsledek bude 1

      People someOtherPeople = new People(); 
       System.out.println(somePeople.peopleCount) // výsledek bude 2

   }

}

Proměnné třídy

Proměnná třídy může být několika typů :

private je viditelná pouze v rámci třídy (classA.variable nefunguje) -> potřebujeme getter

class ClassA(){
   private int variable = 5; // privátní proměnná

   public int getVariable(){ // public getter, který nám dá hodnotu privátní proměnné
       return variable; 
   }


}

public (viditelná i mimo třídu (classA.variable funguje))
protected (chová se jako private, ale pro potomky třídy se chová jako public)

Syntaktická kategorie příkaz a výraz (příkaz vs výraz)

Příkaz (Statement) vyjadřuje činnost, která má být provedena. Příkazy obsahují klíčová slova (while,if, new, return....) a určují vzhled programovacího jazyka Klíčová slova nelze použít jako názvy proměnných. Příkazy nám jsou také schopné vrátit hodnotu.

Výraz (Expression) na rozdíl od příkazu slouží k vyhodnocení. Jeho vedlejším účinkem, výstupem je true nebo false. Není nám schopný vrátit hodnotu a používá se k vyhodnocení, ergo vyhodnotí se na určitou hodnotu.

Např.: $2+5$, $y-6$, $4\neq4$ se vyhodnotí jako NEPRAVDA

Zdroje

Příkaz (programování) Wikipedia : The Free Encyclopedia [online] @2023 [citováno 18.05.2023] Dostupné z: https://cs.wikipedia.org/wiki/P%C5%99%C3%ADkaz_(programov%C3%A1n%C3%AD)
Příkaz (programování) Wikipedia : The Free Encyclopedia [online] @2023 [citováno 18.05.2023] Dostupné z: https://cs.wikipedia.org/wiki/V%C3%BDraz_(programov%C3%A1n%C3%AD)

Datové typy

Primitivní a objektové datové typy. Statické a dynamické typy. Substituční princip.

Primitivní a objektové datové typy

Primitivní datový typ
Jedná se o datový typ, který je atomický. Tedy slouží jako základní stavební jednotka. Tento typ nelze nijak dále dělit. Zabírá fixní místo v paměti, a to v závislosti na konkrétním typu. Primitivní datové typy se nachází v alokované v oblasti, které říkáme zásobník (stack).

Rozlišujeme několik základních datových typů, podle toho, jakou mohou obsahovat hodnotu a podle toho, jak velká tato hodnota může být (kolik místa zabírají v paměti)

int
- jedná se celočíselný datový typ; v paměti zabírá 32 bitů; může tedy obsahovat číselnou hodnotu, která se vejde do 32 bitů
float
- jde o typ s pohyblivou plovoucí čárkou; používá se pro desetinná čísla s přesností 24 bitů; zbytek (8 bitů) je pro exponent
double
- pokud potřebujeme větší přesnost než float, použijeme double
boolean
- vyjadřuje buď hodnotu true, nebo false; v paměti zabírá minimálně velikost registru (minimálně 8 bitů)
long
- také se mu říká long int; v paměti zabírá 64 bitů
char
- jedná se o typ, který pojme jeden znak; velikost je 8 bitů -> převod hodnoty na znak pomocí UTF-8 nebo ASCII tabulky
enum
- velikost 32 bitů defaultně
- neboli výčet identifikátorů a jim přiřazených hodnot; jeho velikost je dána největší velikostí datového typu, který enum obsahuje; pokud máme v enumu int a float, tak enum bude velikosti floatu -> 64 bitů
- v kódu se enum chová jako konstanta
- v jazyce java např. je prvnímu identifikátoru přiřazena hodnota 0 a záleží na pořadí ve výčtu identifikátorů
pointer
- neboli ukazatel, drží v sobě odkaz do paměti -> adresu; jeho velikost je dána velikostí adresního registru;

Objektový datový typ

Je definovaný uživatelem. Objekt je struktura, která obsahuje proměnné a metody. Potřebuje tolik místa, kolik potřebují proměnné a metody obsažené v objektu.

Zatímco primitivní datové typy nemají žádné metody -> nic neumí, tak objekty umožňují provádět operace voláním metod na instanci objektu -> String má například metodu size(), která vrací jeho délku.

Objektové datové typy podporují dědičnost, všechny objekty dědí ze základní třídy Object.

Objektové datové typy jsou alokované v oblasti paměti, které říkáme halda (heap). Ale reference na tento objekt (pointer), je uložena na zásobníku.

Alokace probíhá pomocí klíčového slova new.

Halda vs Zásobník

Pro drtivou většinu jazyků platí, že pokud je proměnná inicializována pomocí new (objekt či jiná dynamicky alokovaná proměnná), tak se alokuje na heapu. Tedy data, která objekt obsahuje, tak jsou alokovaná na heapu. Samotná proměnná si drží adresu, která ukazuje kde tyto data najdeme a je uložena v zásobníku (pointer).

Jsou zde malé rozdíly v jazycích, uvedeme si jako příklad Javu a C++.

V obou případech máme třídu A

class A{ 
    int var; 
}

Pokud chceme vytvořit objekt třídy A, tak v Javě platí to, co je uvedené výše.

A object = new A(); // Na heapu se alokuje 32 bitů a na zásobníku prostor pro adresu, která ukazuje, kde se těchto 32 bitů nachází na heapu

V C++ máme na výběr, kde chceme alokovat

A a; //  Jedná se o klasickou proměnnou, int var je alokována na zásobníku

A* a = new A(); //  Jedná se o referenci, proměnná a je na zásobníku a proměnná var je na heapu -> stejné jako v Javě, akorát bez hvězdičky

U C++ ale platí, že s velkou mocí přichází velká zodpovědnost. Zatímco zásobník si uvolňuje paměť sám, tak halda (heap) vyžaduje, aby ji programátor v C++ uvolnit sám ručně. Jakmile přestane existovat reference v zásobníku na paměť inicializovanou na heapu, tak data již nejsou dostupná, ale stále zabírají místo v paměti. (Java toto nemá, používá tzv. Garbage Collector, který uvolňuje paměť, jakmile referenční proměnné opustí scope). Proto v jazyce C++ používáme např. destruktory, abychom tuto paměť zcela uvolnili.

Pěkné video na heap, stack, uložení jednotlivých proměnných, pointery či dynamickou alokaci paměti si můžete pustit zde

Statické a dynamické typy

Statický typ je takový typ proměnné, který dostal přiřazené místo při deklaraci. Velikost tohoto místa nelze změnit za běhu programu. Velikost je známa a dána při kompilaci. Jedinou možností je explicitní přetypování proměnných - tím změníme velikost paměti dedikovanou pro danou proměnou.

    float a = 15;
    int b;

Už při kompilaci je v paměti vytvořeno místo, pro obě proměnné tohoto typu, nezávisle na tom, zdali jsou inicializované. Primitivní datové typy jsou statické.

Dynamický typ je takový typ proměnné, které může být alokováno místo za běhu programu - runtime alokace.

    A object;

    ///// O nějakou dobu později (program celou dobu běží.....)
    
    object = new A();

Nebylo známo, kolik místa bude proměnná tohoto typu potřebovat při kompilaci. Toto místo ji bylo přiřazeno až při běhu programu. Objektové datové typy jsou dynamické. Opětovným voláním object = new A() později můžeme vytvořit nové místo pro tu samou proměnnou. (Reference zůstává v zásobníku, pouze se změní adresní prostor na heapu, na který odkazuje).

Substituční princip

Jedná se o princip OOP který říká, že objekt (zde instance třídy rodiče), může být nahrazen pod-objektem (instancí třídy potomka) aniž by to rozbilo program.

Potomek může nahradit předka, ale předek nemůže nahradit potomka.

Potomek má alokovanou paměť stejného typu + má něco navíc.
Nemůžme program rozbít ve smyslu přístupu do paměti (samozřejmě, že můžeme v potomkovi přepsat metody předka tak, aby program již nefungoval, ale z hlediska přístupu do paměti může potomek vždy nahradit předka)

Zdroje

Úvod do programování v C++. Jan Fesl [online] @2020 [citováno 18.05.2023]
Dostupné z: https://elearning.jcu.cz/pluginfile.php/47098/mod_resource/content/2/1.pdf
Difference between Stack and Heap Allocation in java, c++, c?. Quora [online] @2014 [citováno 18.05.2023]
Dostupné z: https://www.quora.com/Difference-between-Stack-and-Heap-Allocation-in-java-c++-c
What is the difference between a static and dynamic variable in C language?. Quora [online] @2019 [citováno 18.05.2023]
Dostupné z: https://www.quora.com/What-is-the-difference-between-a-static-and-dynamic-variable-in-C-language
Liskov substitution principle. Wikipedia : The Free Encyclopedia [online] @2023 [citováno 18.05.2023]
Dostupné z: https://en.wikipedia.org/wiki/Liskov_substitution_principle

Řídící struktury jazyka

Složený příkaz resp. blok. Příkazy pro větvení programu (podmíněný příkaz - varianty, vícenásobné větvení). Příkazy cyklu a možnosti jejich ukončení. Strukturování programu pomocí metod, rekurzivita.

Složený příkaz

Jedná se o zapsanou posloupnost příkazů, které se nacházejí v bloku, jež je ohraničený složenými závorkami

{
    int age;
    age = 10;
    System.out.println("My age is: " + age);
}

Jednotlivé bloky mohou být vnořené do sebe

{
    int age;
    age = 10;
    System.out.println("My age is: " + age);

    {
        age = 15;
        System.out.println("My age is: " + age);
    }
}

Je důležité dát pozor na platnost proměnných. Proměnná deklarovaná v bloku je přístupná pouze uvnitř tohoto bloku (a ve vnořených blocích, které jsou rovněž jeho součástí). Jakmile se program dostane mimo tento blok, proměnná přestává existovat (její paměť je uvolněna).

Příkazy pro větvení programu

Program se v určité částí může větvit na dvě části pomocí IF-ELSE tvrzení. Toto tvrzení je podmínka, která se musí splnit pro vykonání IF větve. Tato podmínka může být:

jednoduchá (age > 5)
složená (age > 5 && height > 120)

if (age >= 15) {
    System.out.println("I'm almost an adult");
} else {
    System.out.println("Go home kid");
}

Nebo na více částí pomocí IF-ELSE IF

if (age >= 18) {
    System.out.println("I'm big boy now");
} else if (age >= 15) {
    System.out.println("I'm almost an adult");
} else {
    System.out.println("Go home kid");
}

Platí, že program postupuje odshora dolů a při splnění podmínky se ukončí celý blok -> přeskočí se zbytek if-else tvrzení.

Dalším způsobem jak větvit program je použít switch.

value = 2;

switch (value) {
    case 1:
        System.out.println("one");
        break;
    case 2:
        System.out.println("two");
        break;
    case 3:
        System.out.println("three");
        break;
    default:
        System.out.println("I dont know");
        break;
}

mezi case a break se nachází také blok kódu. Pokud by jsme neměli break, je podmínka vyhodnocena, blok proveden, ale pokračovali by jsme ve vyhodnocování switche.

Obojí může být vnořené do sebe, stejně jako bloky.

if (age >= 18) {
    System.out.println("I'm big boy now");

    if (height > 168) {
        System.out.println("And I'm not a hobbit");
    } else {
        System.out.println("What about second breakfast?");
    }
}

Cykly

Cyklus je blok kódu, který se opakuje dokud:

není naplněna podmínka
není ukončen příkazem break
- namísto ukončení celého cyklu je možné použít příkaz continue pro ukončení aktuální iterace cyklu

Druhy cyklů

For cyklus
While cyklus
Do-While cyklus
For each

For cyklus

Jedná se o cyklus, ve kterém iterujeme dokud není naplněn počet iterací. Ten je uveden v podmínce cyklu. Nejčastěji se jedná o inkrementující se proměnnou (kterou však můžeme upravovat v rámci cyklu), říkáme ji iterátor. Některé datové struktury mají vlastní iterátory -> například struktura HashMap.

for (int i = 0; i > age; i++) {
    System.out.println("Now I'm" + i + "years old" );
}

While cyklus

Zde iterujeme dokud není splněna vstupní podmínka.

while (age > 5) {
    System.out.println("Now I'm" + age + "years old" );
    age++;
}

Do-while cyklus

Obměna while cyklu. I když je podminka nesplněna při vstupu do cyklu, provede se tělo cyklu alespoň jednou.

do {
    System.out.println("Now I'm" + age + "years old" );
    age++;
} while (age > 5)

For each cykly

Tyto cykly iterují nad nějakou kolekcí, prvek po prvku. Velmi používané pro práci s kolekcemi.

for (int number : numberArray) {
    System.out.println(number);
}

Vnořené cykly

Cykly mohou být do sebe vnořené, to se často používá při průchodu vícerozměrných polí. Vnořené cykly značně zvyšují algoritmickou složitost.

for (int i = 0; i > array.size; i++) {
    for (int j = 0; i > array[i].size; j++) {
        System.out.println(array[i,j]); 
    }
}

Strukturování programu za pomoci metod

Pokud chceme udělat nějaký blok kódu volatelným, uděláme z něj metodu.

Výhody užití metod:

zpřehlednění kódu (rozdělení na menší bloky)
redukce duplicit (metody můžeme volat vícekrát)
testování (můžeme testovat konkrétní malou část kódu - metodu)

class Program {

    public static void main(String[] args) {
        method(); // Tady voláme metodu
    }

    public void method() {
        System.out.println("method called");
    }

}

Metoda může přijímat parametry nebo i vracet hodnotu pomocí klíčového slova return. Taková metoda má poté namísto typu void návratový typ.

public void method(int num) {
    System.out.println("method called with number: " + num);
}

public int getSquared(int num) {
    return num * num;
}

Metody je možno volat rekurzivně -> metoda volá zevnitř sebe sama. Je zde nutná nějaká ukončující podmínka, jinak to bude dělat do nekonečna.

class Program {

   public static void main(String[] args) {
       int number = 4;
       int result = 0;

       result = factorial(number);
       System.out.println(number + " factorial = " + result);
   }

   public int factorial(int n ) {
       if (n != 0) { // ukončovací podmínka
           return n * factorial(n-1);  //rekurzivní volání, jednotlivé výsledky jsou po skončení rekurze vynásobeny mezi s sebou
       } else {
           return 1;
       }
   }

}

Zdroje

Recursion is not hard: a step-by-step walkthrough of this useful programming technique. FreeCodeCamp [online] #2018 [citováno: 17.05.2023]
Dostupné z: https://www.freecodecamp.org/news/recursion-is-not-hard-858a48830d83/

Základní pojmy objektově orientovaného paradigmatu

Klíčové pojmy: OOP – objektově orientované programování, třída, objekt, instance třídy, datové složky a metody třídy, konstruktor, parametrizovaný konstruktor.

Třídy a objekty

V podstatě vše, co lze pojmenovat podstatným jménem je objekt (židle, skříň, stůl | tričko, šála, kalhoty). Tyto věci okolo nás lze rozřadit do tříd (konceptů) (Nábytek | Oblečení). U každého konkrétního objektu můžeme poté říct, že je konkrétní realizací některé třídy. Čili, objekt je instance třídy. Třída je obecná (třída je vzor). Objekt je konkrétní.

Každá třída je charakterizována svými vlastnostmi, funkčními možnostmi a parametry.

U každého objektu vnímáme dvě věci: jaké má objekt vlastnosti (student má jméno, příjmení, datum narození, známky ...) a činnosti daného objektu (každý student musí chodit do školy, učit se, psát písemky, ...). Tomu odpovídá zdrojový kód programu: třída se skládá z deklarace proměnných (datových složek, vlastností dané třídy) a definice metod (činnosti dané třídy).

Instance třídy

V programu vytváříme objekty podle předpisu třídy. Tomuto objektu se poté říká instance třídy. Pokud chceme vytvořit instanci, využijeme k tomu operátor new. V následujícím příkladu vytváříme instanci třídy Person.

Person person1 = new Person();

Operátor new alokuje paměť potřebnou pro uložení objektu. Dále následuje volání konstruktoru za pomocí Person(). V proměnné person1 je poté uložena reference na místo v paměti, kde se objekt skutečně nachází.

Konstruktor

Konstruktor slouží primárně pro předání parametrů při vytváření instance třídy. (Ale můžeme si do něj ve výsledku psát cokoliv chceme, aby se s instancí stalo ihned po jejím vytvoření)

Konstruktor je metoda, která se volá vždy při vytváření instance třídy. Ve většině objektově orientovaných jazycích má stejné jméno jako třída.

Rozlišujeme dva druhy konstruktorů:

Implicitní konstruktor
Parametrizovaný konstruktor

Pokud třída konstruktor nemá, používá se namísto toho automaticky tzv. implicitní konstruktor. Jedná se o prázdný konstruktor bez vstupních parametrů. Tento konstruktor nemusíme vytvářet. Má ho každá třída.

Druhou možností je použít parametrizovaný konstruktor, který si přidáme do definice třídy (V našem případě třída Person). Vede nás k tomu několik důvodů:

pomocí parametrizovaného konstruktoru můžeme nastavit hodnoty atributů třídy už při vytváření instance třídy
nastavování hodnot proměnných po jedné je zdlouhavé a nepřehledné
datové složky ve třídě by měli být správně z jiné třídy neviditelné, takže tato úprava by neměla být možná, jen přes speciální metody (get a set)

Parametrizovaný konstruktor je třeba ručně vytvořit, tedy, definovat ho ve třídě. Řekněme. že naše třída Person má atribut Name. My bychom rádi nastavili tento atribut již při vytvoření instance. Definice konstruktoru bude následovná.

public class Person(){

    private String name;

    public Person(String nameFromOutside){
        this.name = nameFromOutside;
    }
}

Pokud budeme nyní chtít vytvořit instanci třídy Person, musíme při inicializaci vyplnit všechny parametry, jež po nás konstruktor požaduje.

Person person1 = new Person("Pája");

Destruktor

Stejně jako se konstruktor volá při vytvoření instance třídy, destruktor se volá, když opouštíme Scope (zjednodušeně chlupaté závorky) ve kterém byla instance vytvořena.

Jedná se o speciální metodu jejíž účelem je uvolnění paměti a zrušení reference. V některých jazycích, jako je například Java, nemusíme destruktor řešit, neboť je implementován automaticky pomocí tzv. garbage collectoru. V jiných, jako je C++, je potřeba ve třídě destruktor ručně definovat a v odpovídající chvíli ho na instanci zavolat.

Metody

Již jsme řekli, že třída se skládá z datových složek (proměnných) a definic metod. Metoda je něco, co třída umí.

Metody určují chování objektu
Definují operace nad daty objektu
Metody představují služby objektu, proto jsou často veřejné
Metody mohou vracet hodnoty
Mohou být deklarovány jako privátní, např. pro pomocné funkce/výpočtu zlepšující čitelnost kódu.

Volání metod

Samotnou deklarací (napsáním kódu) metody se žádný kód neprovede.
Chceme-li vykonat kód metody, musíme ji zavolat.
Volání se realizuje (tak jako u proměnných) "tečkovou notací", viz dále.
Při volání metody je možné předat metodě parametry
Volání lze provést, jen je-li metoda z místa volání přístupná - "viditelná". Přístupnost regulují podobně jako u proměnných modifikátory přístupu.

Statické proměnné a metody

Doteď každá proměnná nebo třída patřili vždy určitému objektu. (instanci třídy)

Lze deklarovat také metody a proměnné patřící celé třídě, tj. skupině všech objektů daného typu - statická proměnná existuje pro jednu třídu jen jednou.

Takové metody a proměnné nazýváme statické a označujeme v deklaraci modifikátorem static.

Statická třída

Statická třída je taková třída, jejíž všechny prvky (proměnné i metody) jsou statické.

Modifikátory přístupu

Účelem modifikátorů přístupu je implementace enkapsulace, která je jedním ze základním principů OOP.

Modifikátory přístupu říkají, které další třídy mohou mít přístup k proměnné nebo metodě.

private - pouze aktuální třída má přístup k proměnné či metodě
protected - pouze aktuální třída a její potomci mají přístup k proměnné či metodě
public - jakákoliv třída má přístup k proměnné či metodě. (Pokud není metoda statická, je třeba stále mít referenci na instanci třídy, ve které se tato public metoda nachází)

4 základní principy OOP

Aby jazyk vyhovoval objektově orientovanému paradigmatu, musí umožňovat dosažení 4 následujících věcí

Enkapsulace
Dědičnost (Viz okruh 2.4.5)
Polymorfismus (Viz okruh 2.4.5)
Abstrakce (Viz okruh 2.4.6)

Enkapsulace

Zapouzdření kombinuje data a metody do jednoho celku. Hlavním cílem zapouzdření je zabezpečení dat. Dosažení zapouzdření je možné pomocí modifikátorů přístupu public, protected a private. Mění viditelnost dat nebo metod. Soukromí členové jsou přístupní pouze v rámci třídy, zatímco veřejní členové jsou přístupní v rámci třídy a jiných tříd.

Zapouzdření v jazyce OOP je možné implementovat tak, že se členové dat nebo vlastnosti zpřístupní prostřednictvím veřejných metod, jako jsou gettry a settry. Podobně enkapsulace komprimuje data a metodu do jedné jednotky. Navíc poskytuje ochranu dat.

V jednoduchosti: Metody i data jsou zapouzdřeny ve třídě. Data mají modifikátor přístupu private. K přístupu k datům (získání či nastavení hodnoty) se využívají speciální metody. Gettry a settry. Tyto metody mají modifikátor přístupu public.

Citace

Objektově orientované programovaní [online] ©2015 [cit. 3.12.2022] ČVUT Jan Faigl. Dostupné z: https://cw.fel.cvut.cz/old/_media/courses/a0b36pr1/lectures/lecture07-handout.pdf
Methods (OOP) Brilliant.org [online] ©2022 [cit. 3.12.2022] Brilliant.org. Dostupné z : https://brilliant.org/wiki/methods-oop/
Objektově orientované programování. [online] ©2004 [cit. 3.12.2022] František Dařena. Dostupné z: https://akela.mendelu.cz/~darena/Perl/objekty.html

Dědičnost a polymorfismus

Dědičnost aneb jeden ze základních principů OOP

Dědičnost je jedna ze základních vlastností OOP a slouží k tvoření nových datových struktur na základě starých. Inspirace je (jako u všech aspektů OOP) ve skutečném světě. Pro implementování dědičnosti potřebujeme rodiče (předka) a dítě (potomka). Potomek přebírá atributy (proměnné) předka i jeho schopnosti (metody). Potomek tedy "vylepšuje" předka, neboť má vše, co předek, + své věci navíc.

V okruhu 2.4.4 se bavíme o modifikátorech přístupu. Víme, že prvek (proměnná, či metoda) může být public (všude viditelná), private (viditelná pouze v rámci třídy ke které náleží) a protected. protected se používá právě v rámci dědičnosti a říká, že prvek je viditelný ve třídě, které náleží a ve všech potomcích této třídy. Pokud je modifikátor přístupu prvku jiný než public, nelze k němu přistupovat zvenčí (Nelze k němu přistupovat skrze instanci).

Na následujících obrázcích se nachází příklad dědičnosti. Všimněme si aplikování modifikátorů přístupu.


obr. 1: Rodičovská třída Vlastní zdroj

Třída Shape je rodič. Obsahuje privátní atribut color. K tomuto atributu nelze přistupovat jinde, než v rámci této třídy.

Znamená to, že následující kus kódu vyhodí chybu.

Shape s = new Shape();
s.color = "black"; // Nemůžeme přistoupit k proměnné color skrze instanci, protože je private.

Skrze instanci můžeme přistupovat pouze k veřejným členům třídy.

Shape s = new Shape();
s.setColor("black") // Toto je správně, metoda setColor je public.

Speciálním případem je modifikátor protected. Při přístupu skrze instanci se chová stejně, jako private. protected string type; Rozdíl je, že k tomuto prvku můžeme přistupovat v potomcích třídy Shape. Viz metoda init() ve třídě Triangle.


obr. 2: Potomek třídy Shape Vlastní zdroj

Ač atributy perimeter a area nikde ve třídě Triangle nevidíme, v metodě init() k nim přistupujeme. Je tomu tak proto, že třída Triangle rozšiřuje svého rodiče, třídu Shape. A jak jsme řekli výše, potomek obsahuje to samé, co rodič + něco navíc. (Atributy a, b, c).

Pozor: Pokud je atribut rodičovské třídy private a potomek ho nevidí, neznamená to, že potomek tento atribut neobsahuje. V našem příkladu potomek nemůže přímo přistupovat k atributu color, ale může k němu přistupovat skrze metody setColor() a getColor(). Říkáme, že potomek zdědil atribut color jako private (privátní).

Ve výsledném programu bude využití našich dvou tříd následující.


obr. 3: Využití dědičnosti v praxi Vlastní zdroj

Za zmínku stojí řádek Console.WriteLine(t.getType()). Proč nemůžeme napsat Console.WriteLine(t.type)?. Protože atribut type je protected. Zde bychom se snažili přistoupit k protected atributu zvenčí (skrze instanci), což nelze.

Celému tomuto principu, jež jde ruku v ruce s dědičností se říká enkapsulace (viz okruh 2.4.4).

Přiřazení hodnoty mezi předkem a potomkem

Poněvadž platí, že potomek obsahuje to samé co předek, + něco navíc, tak můžeme předkovi přiřadit potomka. Naopak to nejde, protože potomek má některé atributy navíc, které by zůstaly "nevyplněny"

Shape s = new Triangle(a,b,c); // Tato je to správně. Deklarujeme nový objekt typu Shape. A tomuto objektu říkáme, budeš trojúhelník.

Triangle T = new Shape(); // Toto je špatně. A ani to z logického hlediska nedává smysl.

Předek může samozřejmě mít potomků více.

Triangle t = new Triangle(a,b,c,);
Square s = new Square(a);
Circle c = new Circle(r);

List<Shape> shapes = new List<Shape>();
//Stále platí to samé, předkovi lze přiřadit potomka, nikoliv naopak.
shapes.add(t);
shapes.add(s);
shapes.add(c);

Hierarchie volání konstruktoru

Při vytváření potomka platí, že první se zavolá konstruktor předka a poté se volá konstruktor odpovídajícího potomka. Konstruktory se volají tzv. zdola nahoru. Pokud má tedy předek také svého předka, volá se první konstruktor tohoto předka.


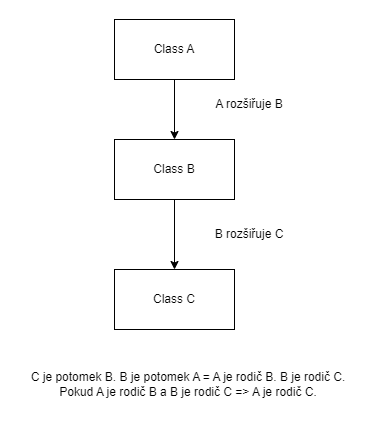obr.4: Hierarchie dědění Vlastní zdroj

Vícenásobná dědičnost

Stejně jako může předek mít potomka, tak může i potomek mít svého potomka. Aplikují se stejná pravidla při dědění, jako v předchozím případě. Všechno co má rodič, má i potomek.


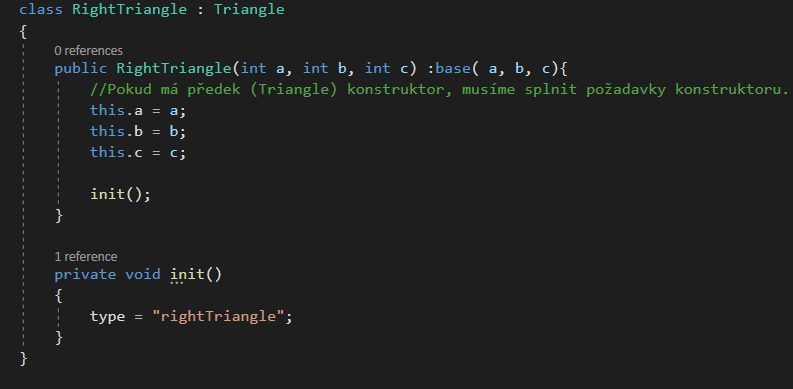obr.5: Dědění z potomka Vlastní zdroj

V některých jazycích, jako je například C++, je možné dědit z více předků zároveň. Potomek v takovémto případě dědi atributy i metody ze dvou tříd. Stejně tak se volají konstruktory těchto tříd před zavoláním třídy potomka. Dědičnost v C++ zde.

Virtuální metody, přepisování metod

Výše uvedených vlastností dosáhneme implementací tzv. virtuálních metod. Jedná se o metody předka, které může potomek přímo přepsat. Pokud poté přiřadíme předkovi potomka a na tohoto potomka zavoláme metodu, kterou přepsal, vykoná se metoda potomka. Pokud bychom metodu v předkovi jako virtual neoznačili a poté ji v potomkovi nepřepsali, vykonala by se metoda předka. (Viz příklad, obrázek č. 6).

Implementace těchto metod se liší v závislosti na jazyku. v C# a C++ k tomu slouží prefix virtual v rodičovské třídě a prefix override v potomkovi. V Javě jsou všechny metody přirozeně virtuální, není tedy třeba specifikovat v rodiči, které lze přepsat, neboť jdou pomocí anotace @Override přepsat všechny (pokud jejich hlavička neobsahuje klíčové slovo final).

Následuje příklad jednoduché dědičnosti bez virtuálních metod.


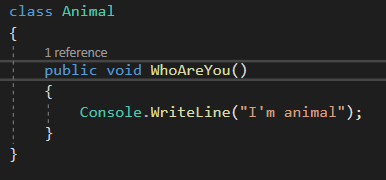obr.6: Nevyužití virtuálních metod: předek Vlastní zdroj


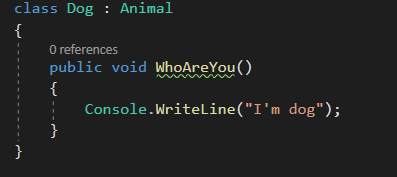obr.7: Nevyužití virtuálních metod: potomek Vlastní zdroj


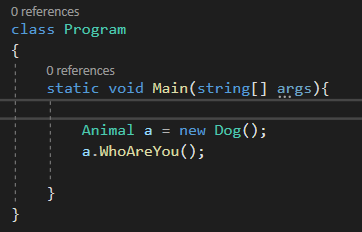obr.8: Volání stejně pojmenované metody v předkovi i v potomkovi Vlastní zdroj


obr.9: Výstup Vlastní zdroj

Můžeme vidět, že k přepsání nedošlo (Kdybychom použili Dog d = new Dog();, tak by nebyl problém). Ale logicky, by k přepsání dojít mělo. Máme zvíře ( Animal a), zvíře je pes(a = new Dog();). A my se zvířete (ne přímo psa) ptáme "co jsi zač?". Důvodem, proč se tak nestalo je fakt, že ač jsme do instance třídy Animal uložili objekt typu Dog, tak ukazatel tohoto objektu d stále ukazuje na typ Animal. Což by se nestalo při Dog d = new Dog();.

Pojďme to zkusit znovu, tentokrát s využitím virtuálních metod.


obr.10: Využití virtuálních metod: předek Vlastní zdroj


obr.11: Využití virtuálních metod: potomek Vlastní zdroj


obr.12: Volání stejně pojmenované metody v předkovi i v potomkovi Vlastní zdroj


obr.13: Výstup Vlastní zdroj

Nyní dostáváme chtěný výstup. Důvodem je tzv. Tabulka virtuálních metod. Jedná se o vnitřní strukturu, která si drží informace o tom, jaký potomek přepisuje jakou virtuální metodu v jakém předkovi. Virtuální metody jsou základním způsobem dosažení polymorfismu.

Čistě virtuální metody

Jedná se o metody, které nemají tělo a pokud je potomek zdědí, MUSÍ je implementovat. Pokud třída obsahuje jenom čistě virtuální metody, nazývá se Interface. Viz. okruh 2.4.6

Polymorfismus aneb jeden ze základních principů OOP

Polymorfismus je vlastnost programovacího jazyka, speciálně v objektově orientovaném programování, která umožňuje objektům volání jedné metody se stejným jménem, ale s jinou implementací.

Polymorfismus umožňuje:

jednomu objektu volat jednu metodu s různými parametry (ad-hoc polymorfismus);
objektům odvozeným z různých tříd volat tutéž metodu se stejným významem v kontextu jejich třídy, často pomocí rozhraní;
přetěžování operátorů neboli provedení rozdílné operace v závislosti na typu operandů;
jedné funkci dovolit pracovat s argumenty různých typů (parametrický polymorfismus, ne ve všech programovacích jazycích).

Implementace polymorfismu se různí, nejčastěji ji lze dosáhnout za pomocí abstraktních tříd a interface Viz. okruh 2.4.6 .Implementací polymorfismu dosáhneme abstrakce.

Citace

Polymorfismus [online] ©2021 [cit. 4.12.022] Wikipedie. Dostupné z: https://cs.wikipedia.org/wiki/Polymorfismus_(programov%C3%A1n%C3%AD)
Dědičnost, spřátelenost [online] ©2021 [cit. 4.12.2022] Jan Fesl. Dostupné z: https://elearning.jcu.cz/pluginfile.php/47104/mod_resource/content/2/10.pdf
Exploring virtual and abstract methods in C#. [online] ©2015 [cit. 5.12.2022] Joydip Kanjilal. Dostupné z: https://www.infoworld.com/article/2895408/exploring-virtual-and-abstract-methods-in-c.html

Abstraktní třídy, interfejsy a jejich implementace

Abstraktní třída

Abstraktní třída je obyčejná třída, která jenom nemá definované některé metody; předpokládá se, že nějaká jiná třída z ní bude dědit a tyto metody si doplní podle potřeby.

Je to hybrid mezi rozhraním (interface) a klasickou třídou. Od klasické třídy má schopnost implementovat vlastnosti (proměnné) a metody, které se na všech odvozených třídách budou vykonávat stejně. Od rozhraní zase získala možnost obsahovat prázdné abstraktní (čistě virtuální) metody, které si každá odvozená podtřída musí naimplementovat sama. S těmito výhodami má abstraktní třída i pár omezení, a to že jedna podtřída nemůže zdědit víc abstraktních tříd a od rozhraní přebírá omezení, že nemůže vytvořit samostatnou instanci (operátorem new).

Klasické využítí abstraktní třídy je, pokud potřebujeme vágního, společného předka. Příkladem může být třída Shape a její potomoci Cirle, Sphere a Square. Potomci třídy mají společné vlastnosti a metody, jež se nachází ve třídě Shape (například proměnná barva, metoda changeColor, nebo metoda Render). Třída Shape bude abstraktní, protože nemá smysl, aby existoval objekt typu Shape. Ale má smysl, aby existoval objekt typu Square, který dědí ze abstraktní třídy Shape. V našem příkladu je v třídě Shape prázdná proměnná Color, čímž říkame, že každý potomek této třídy musí mít barvu, předem vyplněná (implementovaná) metoda changeColor a prázdná metoda Render, jež si musí potomci třídy implementovat zvlášť.

Abstraktní třída

může obsahovat instanční proměnné
může obsahovat konkrétní metody i metody bez implementace
dědění z (abstraktní) třídy vylučuje možnost dědit z jiné třídy

Interface

Interface je seznam čistě virtuálních metod, které by měla třída podporovat, aby plnila nějaký účel. Jestliže se třída hlásí k tomu, že podporuje daný interface, musí definovat všechny metody, které předepisuje interface a tím je přepsat.

Interface předepisuje třídě, která od ní bude odvozena, jaké metody (případně properties) musí implementovat. Odvozený objekt může implementovat i další metody. Interface nedefinuje žádné proměnné ani neobsahuje naimplementované metody (pouze jejich hlavičky). Přitom třída může implementovat libovolný počet rozhraní (na rozdíl od dědičnosti).

Klasické využití interface (rozhraní) je příklad, kdy máme několik různých tříd, u kterých nemá smysl, aby dědily ze stejného předka (světlo, sekačka, rádio), ale tyto třídy mají některé stejné vlastnosti (spínač). Je tedy nasnadě, aby tyto třídy implementovali stejný interface s metodou turnOn / turnOff. Každá třída poté bude mít vlastní implementaci této metody.

Implementace interface

Implementaci interface můžeme dělit na

implicitní
explicitní

Implicitní implementace interface

Třída T, která interface I implementuje má implementované metody implementované napřímo (public void interfaceMethod1)
Metody jsou volatelné na objektu typu T
Metody jsou volatelné na objektu typu I
Metody jsou volatelné na potomcích třídy T


obr. 1: Implicitní implementace Dostupné z: https://www.pluralsight.com/guides/distinguish-explicit-and-implicit-interface-implementation-csharp

Explicitní implementace interface

Třída T, která interface I implementuje má implementované metody skrze interface (public void ourInterface.interfaceMethod1)
Metody nejsou volatelné na objektu typu T
Metody jsou volatelné na objektu typu I
Metody nejsou volatelné na potomcích třídy T


obr. 2: Explicitní implementace Dostupné z: https://www.pluralsight.com/guides/distinguish-explicit-and-implicit-interface-implementation-csharp

pozn. Zatímco implicitní implementace je možná téměř všude, explicitní implementace není možná například v jazyce Java. (ale v c# ano).

Interface (rozhraní)

nesmí obsahovat proměnné
všechny metody jsou bez implementace
do jedné třídy lze implementovat více rozhraní (Řešení problému vícenásobné dědičnosti)

Typy interface

Interface, jako takový, můžeme dělit na dva typy. (Neplést si s implementací interface, viz výše)

implicitní interface (public metody)
explicitní interface (musí se napsat struktura Interface a poté implementovat)

Explicitní interface

Jedná se o interface, který musíme vytvořit a naimplementovat. (viz výše, implementace interface)

Implicitní interface

Jedná se o public metody třídy. Skrze tyto třídy přístupujeme k objektu. Je to tedy jakési jeho rozhraní (interface).

Abstraktní třídy a Interface jsou jedněmi ze základních nástroju pro dosažení polymorfismu. Viz. okruh 2.4.5

Citace

Jaký je rozdíl mezi abstraktní třídou a interface? [online] ©2015 [cit. 2.12.2022] Ivo Kostecký. Dostupné z: https://blog.kostecky.cz/2015/06/jaky-je-rozdil-mezi-abstraktni-tridou.html
Třídy, polymorfismus [online] ©2022 [cit. 2.12.2022] Fakulta elektrotechnická České vysoké učení technické. Dostupné z: https://cw.fel.cvut.cz/old/_media/courses/a0b36pr2/lectures/02/36pr2-02_tridyiii.pdf
Distinguishing the Explicit and Implicit Interface Implementation in C# [online] ©2015 [cit. 3.12.2022] Christian Findlay. Dostupné z: https://www.pluralsight.com/guides/distinguish-explicit-and-implicit-interface-implementation-csharp
Implicit and Explicit InterfaceExamples [online] ©2022 [cit 3.12.2022] C#Corner. Dostupné z: https://www.c-sharpcorner.com/UploadFile/8911c4/implicit-and-explicit-interface-examples/

Databázový systém

Databázový systém, data, databáze, systém řízení báze dat (SŘBD/DBMS), typy DBMS, relační, objektové, postrelační DBMS.

Databázový systém je program, který se zaměřuje na ukládání, modifikaci a výběr velkého množství dat. Databázový systém se skládá z:

databáze
SŘBD (systém řízení báze dat)
- raději používejte pojem Database Management System (DBMS)!

Protože databázový systém je zodpovědný za práci s velkým množstvím perzistentních (trvalých/uložených) dat, tak jsou na něj kladeny jisté nároky:

podpora pro definice datového modelu (logický, relační)
využití některého z jazyků (SQL,QBE atd.) vyšší úrovně pro manipulaci s daty
správa transakcí
autentizace uživatelů a autorizace operací nad daty
robustnost a zotavitelnost po chybách beze ztráty dat spravovaných systémem

Databáze + program na manipulaci databáze (DBMS) = Databázový systém

Data

Data jsou uložena v databázi. Data jsou surovou matérií: 1, II, Bruno, obrázek domečku. Data se stávají informací jen a pouze tehdy, pokud datům dáme kontext, strukturu: 1. patro v budově, II značí 2 antické sloupy, Bruno je pilot letadla, obrázek domečku je domovská stránka v browseru.

Databáze

Definice: Systém pro ukládání dat s pevnou strukturou záznamů.

S databází je možno manipulovat pomocí DBMS. Databáze nemusí být v elektronické podobě, jako předchůdce databází se uvádí kartotéka -> umožňovala třídění dat podle různých kritérií a zařazování nových dat (záznamů).

Databáze a DBMS není to samé

Pokud budeme hledat, zjistíme že se termín databáze často zaměňuje s termínem systém řízení báze dat. Databáze v databázovém systému je pouhopouhá struktura pro ukládání dat -> báze dat. Tato struktura je spravována a definována pomocí DBMS.

Systém řízení báze dat

Jedná se o software, jež nám umožní provádět operace nad databází. Tvoří rozhraní mezi aplikací a uloženými daty v databázi (bází dat).

Aby byl nějaký systém považován za DBMS, musí být nejen schopný pracovat s velkým množstvím dat, ale musí být schopný i řídit (mazat, vkládat, modifikovat) a definovat strukturu těchto dat. Liší se tím od klasického souborového systému.

DBMS jsou schopné i databáze vytvářet -> definovat strukturu dat.

Systémy pro řízení báze dat můžeme dělit podle toho, jakým způsobem definují strukturu databáze.

Hierarchické (data jsou uspořádána ve stromové struktuře)
Síťové (založen na Hierarchicke struktuře, ale navíc poskytuje vztahy n:m)
Relační (založen na relačním modelu -> je založena na tabulkách, řádky jsou záznamy a sloupce atributy. Některé sloupce mohou obsahovat klíče které uchovávají vztahy mezi tabulkami)
Objektové (na rozdíl od relačního modelu jsou zde tabulky nahrazeny objekty)
Objektově relační (kombinace relačního a objektového -> objekty místo tabulek, klíče jež symbolizují vztahy mezi objekty)

Relační

Jedná se o systém, který nám umožní řídit a definovat strukturu relační databáze

Relační databáze je struktura dat, která nám umožní identifikovat a přistupovat k záznamům podle toho, v jakém jsou vztahu s jinými daty. Data jsou organizovány do relací (tabulek).

Každá tabulka obsahuje řádky (záznamy) a sloupce (atributy). Atribut je vždy nějakého typu.

Většina relačních systému řízení báze dat využívá pro manipulaci relační databáze jazyk SQL.

Objektové

Jedná se o systém, který nám umožní řídit a definovat strukturu objektové databáze

Objektová databáze je struktura, ve které namísto tabulek používáme objekty. Tyto objekty jsou stejné, jako známe z objektově orientovaného programování. Databáze řízené tímto systémem mají jednotlivé vztahy mezi daty uložené přímo v sobě, na rozdíl od relačních, které je mapují pomocí tabulek. Povětšinou jsou tyto vztahy reprezentovány pomocí ukazatelů.

Pro manipulaci objektové databáze je možné použít objektově orientované jazyky.

Výhodou těchto systému je možnost lepší práce s bází dat. Mapování dat na objekty bývá složitý proces a v relačních systémech se to musí dělat ručně, avšak můžeme si usnadnit práci pomocí Object-relational mapping (ORM) (C# někdo ?).

Post-relační

Jde o rodinu databázových systémů, které rozšiřují klasický relační systém

Tyto databázové systémy se odchylují od klasického relačního modelu, jež má striktní strukturu (data jsou v tabulkách, tabulky mezi s sebou mají vztahy pomocí primárních a cizích klíčů, normalizace, ACID....)

Vlastně můžeme říct, že v dnešní době se databázové systémy dělí na dva typy. Ty, které jsou relační, a ty které ne.

Objektový databázový systém je také post-relačním systémem.

Některé další příklady post-relačních systémů jsou:

NoSQL
- využívá jako systém řízení báze dat MongoDB; používá se, pokud máme velké množství nestrukturovaných, nebo polo-strukturovaných dat
Grafové databáze
- používají se pro modelování komplexních vztahů mezi entitami; jako systém řízení báze dat lze využít například Neo4j
Dokumentové databáze
- využívají k ukládání dat dokumentové struktury, povětšinou typu JSON; pro řízení báze dat můžeme využít MongoDB

Pokud databáze není relační, tak je post-relační.

Zdroje

Co je databázový systém. Sprava-site.eu [online] @2022 [citováno 18.05.2023]
Dostupné z: https://www.sprava-site.eu/databazovy-system/
Systém řízení báze dat. Wikipedie : Otevřená encyklopedie [online] @2022 [citováno 18.05.2023]
Dostupné z: https://cs.wikipedia.org/wiki/Syst%C3%A9m_%C5%99%C3%ADzen%C3%AD_b%C3%A1ze_dat
Relational database. Wikipedia : The Free Encyclopedia [online] @2023 [citováno 18.05.2023]
Dostupné z: https://en.wikipedia.org/wiki/Relational_database
What is a Relational Database Management System?. Codecademy Team [online] @2022 [citováno 18.05.2023]
Dostupné z: https://www.codecademy.com/article/what-is-rdbms-sql
What Is an Object-Oriented Database?. MongoDB [online] @2022 [citováno 18.05.2023]
Dostupné z: < https://www.mongodb.com/databases/what-is-an-object-oriented-database>

SQL

historie jazyka, DDL, DML, DCL, TCL

SQL - Structured Query Language je deklarativní a doménově orientovaný jazyk. Zároveň je lidsky čitelný.

Deklarativní znamená, že se neptáme jak něco udělat, ale co se má udělat.

Doménově orientovaný znamená, že SQL můžeme použít jen pro určitou věc -> manipulaci s daty v SŘBD.

Historie SQL

1970 - E.F. Todd - vymyslel relační model pro správu databází, článek A relational Model of Data for Large Shared Data Banks

1974 - v IBM vymysleli Structured English Query Language (SEQUEL)

1980s - vývoj SŘBD Oracle, Sybase, DB/2

1987 - první standard ANSI SQL-86 (SQL1)

1989 - SQL-89 (přidána integritní omezení)

1992 - SQL-92 (SQL2) - přidány transakce a nové datové typy

1999 - SQL:1999 (SQL3) - přidány regulární výrazy a prvky procedurálního programování (proměnné, rekurzivní volání, triggery) a strukturované datové typy

Následovali další standardy: SQL:2003, SQL:2006, SQL:2008, SQL:2011, SQL:2016. Dále podpora XML a JSON, automaticky generované sloupce.

Syntaxe SQL

SQL je ANSI standard
mohou však existovat nuance v zápisu pro různé SŘBD, jednotlivé SŘBD pak mají rozšíření platná pouze pro ně
SQL výrazy nejsou case-sensitive, pro odlišení se však píší velkými písmeny
většina SŘBD vyžaduje po SQL příkazu středník, tak aby bylo možné odlišit více příkazů zadaných společně na vstupu

Datové typy v SQL

mohou se lišit dle SŘBD
mezi základní skupiny patří:
- Textové (CHAR, VARCHAR, NVARCHAR, TEXT, ...)
- Číselné (INT, DECIMAL, NUMERIC, FLOAT, DOUBLE, ...)
- Datum/čas (DATE, TIME, DATETIME, YEAR, ...)
- Ostatní (BIT, BITARRAY, GPS, XML, IMAGE, ...)

Další datové typy můžete nalézt např. zde

Příkazy jazyka SQL

Data Manipulation Language (DML) - pro manipulaci s daty
- SELECT: výběr dat z databáze, výběr podmnožiny
- INSERT: vložení nových dat do databáze
- UPDATE: mění data v DTB (editace)
- MERGE: kombinace INSERT a UPDATE, pokud není odpovídající klíč, tak data vloží, jinak je upraví
- DELETE: odstraňuje záznamy z DTB
- EXPLAIN: speciální příkaz, který zobrazuje postup zpracování SQL příkazu
- SHOW: zobrazuje DTB, tabulky či jejich definice
Data Definition Language (DDL) - vytvářející či upravující strukturu DTB
- CREATE: vytvoření nových objektů
- ALTER: změny existujících objektů
- DROP: odstraňování objektů
Data Control Language (DCL) - řízení uživatelských práv
- GRANT: přidělí userovi oprávnění k určitým objektům
- REVOKE: odejme práva userovi
Transaction Control Language (TCL) - řízení transakcí
- START TRANSACTION (BEGIN): zahájení transakce
- COMMIT: potvrzení transakce
- ROLLBACK: zrušení transakce, návrat do původního stavu
OSTATNÍ - příkazy pro nastavení systémových parametrů, přidávání uživatelů
- SET: (kódování, časová zóna, )

SELECT - standardně se uvádí v DML, ale samotný příkaz SELECT se někdy uvádí jako Data Query Language - DQL, až když se k příkazu SELECT doplní klauzule:

WHERE: zadání podmínek filtrů
GROUP BY: seskupování záznamů
HAVING: zadání podmínek nad agregační funkcí
ORDER BY: seřazení dat

Syntaxe příkazu:

SELECT
FROM
WHERE
GROUP BY
HAVING
ORDER BY

Konkrétní případy použití na WIKI nebo na YT :D

ZDROJE

https://cs.wikipedia.org/wiki/P%C5%99%C3%ADkazy_jazyka_SQL
https://elearning.jcu.cz/pluginfile.php/194326/mod_resource/content/1/SQL_uvod.pdf

Postup návrhu databáze

Postup návrhu databáze, analytik, designér, kodér, analytický model, konceptuální model, fyzický model.

Analytický model

Jedná se o model, který nám říká, co bude databáze obsahovat. Vytváří ho analytik na základě požadavků klienta.

Na analytický model se můžeme také divat z jiného úhlu pohledu. Když je již databáze vytvořena, můžeme v budoucnu chtít v ní existující data analyzovat. (například pomocí regresní analýzy, kdy chceme vědět, jaké vztahy spolu jednotlivé proměnné mají).

Konceptuální model

Zaobírá se popisem významu dat v databázi nezávisle na fyzickém uložení dat.

Samotná data mohou mít podobu například 03.12.2021, 30, Škoda, Martin Jelínek. Z toho můžeme odhadnout, že se jedná o nějaký datum, spojený s nějakým jménem a autem a jako bonus tam je nějaké číslo. Nevíme, co jednotlivé údaje znamenají. Jedná se o datum zapůjčení automobilu, nebo jeho vrácení ? Je 30 doba zapůjčení ?

Konceptuální modely se snaží vytvořit konceptuální pohled člověka na danou část reálného světa. Používáme k tomu E-R model (Entitně relační model). Existují i další konceptuální modely (například hierarchický model, síťový model), přičemž tím nejjednodušším typem modelu, zároveň sloužícím jako omezení pro vyjádření všech dalších je přirozený jazyk.

E-R model

Jedná se o množinu pojmů které nám umožní na konceptuální úrovni abstrakce popsat uživatelskou aplikaci za účelem následné specifikace struktury databáze.

Tento model identifikuje:

typy entity jako třídy objektů stejného typu (Zákazník, Zaměstnanec, ...)
typy vztahů, do kterých mohou entity vstupovat (např. Zákazník MÁ PŮJČENÉ (to je ten vztah) Auto)
na základě jisté úrovně abstrakce přiřadí jednotlivým entitám a vztahům atributy:
jméno, příjmení, ...
formuluje různá integritní omezení např:
- doména atributu VÁHA je reálně číslo
- RDONE_CISLO je identifikačním klíčem entity typu ZAMESTNANEC
- Hodnota atributu A musí být větší než hodnota atributu

Více o E-R modelu lze nalézt v okruhu Entitně relační model.

Fyzický model

Jde o způsob toho, jak jsou data uložena. Nazývá se relační model.

Určuje strukturu tabulek, názvy sloupců (atributů), primary key dané tabulky, foreign key a index sloupce tabulky, ke kterému se váže, relační vztahy mezi tabulkami, uložené procedury a views.

View: Virtuální tabulka. Obsah této tabulky je definován na základě query (tedy je výstupem vykonání query).

Konečný uživatel je od této vrstvy odstíněn SŘBD (Systém řízení báze dat), častěji nazývaným anglicky - DBMS (Database management system), například MySQL.

Postup návrhu databáze

Na počátku existuje zákazník, který má přání na to, že chce vytvořit databázi. Tento zákazník o databázích neví povětšinou zhola nic.

Jeho požadavek si vyslechne analytik, který vytvoří analytický model. Už tedy víme, co bude databáze obsahovat.

Na základě toho, co bude databáze obsahovat, designér udělá konceptuální model (někde se uvádí, že analytický a konceptuální je totéž). Ten již obsahuje databázi z pohledu reálného světa. Schéma uložení dat. Není závislý na konkrétním fyzickém modelu, je zde tedy míra abstrakce.

Na základě tohoto modelu lze vytvořit fyzický model. K tomuto fyzickému modelu přistupují kodéři skrze SŘBD a jsou schopní ho buď manipulovat (rozšiřovat, měnit), nebo vytvářet views.

Views jsou určeny po koncového uživatele. Jedná se o výstup z databáze za pomocí query. Struktura tohoto view nemusí a často nemá s fyzickým model (tím jak jsou data skutečně uložena) nic společného.

Příkladem může být že po vybrání časové rozsahu a kliknutí na tlačítko se uživateli zobrazí, jaká auta jsou v tomto časovém intervalu kým vypůjčena. Jedná se o virtuální tabulku, která byla vytvořena z několika dalších na základě jejich spojování. To, jak koncový uživatel vidí data, neodpovídá tomu, jak jsou fyzicky uložena.

Zdroje

Sandra Suszterova. Physical Data Model vs. Logical Data Model [online] @2023 [citováno: 01.05.2023]
Dostupné z: https://www.gooddata.com/blog/physical-vs-logical-data-model/
Střední průmyslová škola Brno. Databáze – úvod [online] @2023 [citováno: 01.05.2023]
Dostupné z: https://moodle.sspbrno.cz/pluginfile.php/1950/mod_resource/content/1/databaze-uvod.pdf
Michal Valenta. Katedra softwarového inženýrství Fit. České vysoké učení technické v Praze. DBS – Databázové modely. [online] @2023 [citováno: 01.05.2023]
Dostupné z: https://users.fit.cvut.cz/valenta/doku/lib/exe/fetch.php/bivs/dbs_02_databazove_modely.pdf
Wikipedia : Free encyclopedia. Database abstraction layer. [online] @2022 [citováno 01.05.2023]
Dostupné z: https://en.wikipedia.org/wiki/Database_abstraction_layer

Entitně relační model

Relační datový model

Normalizace relačního modelu

Transakční zpracování dat

Řízení konkurenčního přístupu k datům

řízení konkurenčního přístupu k datům, binární zámky, víceúrovňové zámky, časové známky, multiverze

Úvod

Velkým problémem u transakcí je zajistit jejich sériovost. Transakce se skládají z jednotlivých operací. Tyto operace zabírají různý čas.

V jedu chvíli mohou dvě transakce operovat nad stejnou hodnotou a navzájem si ji měnit pod rukama. Příkladem může být scénář, kdy dvě transakce provádějí operace nad dvěma bankovními účty.

jedná hodnotu čte a začne ji upravovat
druhá transakce začne dělat to samé, přečte tu samou hodnotu a začne ji upravovat
jedna z těchto transakcí nevyhnutelně zapíše upravenou hodnotu zpět jako první
ta druhá poté při svém zápisu přepíše výsledek


obr. 1: Špatná posloupnost konfliktních operací

Řízení konkurenčního přístupu k datům zajišťuje správnou posloupnost (řazení) konfliktních operací

Máme několik prostředků, jak toho docílit:

zamykání dat (zabrání vícenásobnému současnému přístupu k datům) - je řízeno pomocí manažera zámků, který spravuje zámky skrze tabulku zámku, ve které jsou záznamy o tom, jaká transakce zamkla jakou položku.
- binární zámky
- víceúrovňové zámky
časové známky (zajišťují sériovost transakčních scénářů - nejdříve jedna, pak druhá)
multiverze (používání více verzí dat)

Binární zámky

Tento zámek je svázaný s danou položkou a určuje, které operace je na ni možné provádět. Může nabývat dvou hodnot 1 - zamčeno, 0 - odemčeno.

Postup aplikace binárního zámku:

transakce se pokusí zamknout hodnotu, se kterou chce pracovat, pokud je tedy hodnota odemčená
pokud je hodnota zamčená, transakce čeká, dokud se hodnota neodemkne
- transakce NESMÍ odemknout zámek hodnoty, kterou sama nezamkla
- jakmile se odemkne, transakce se opět pokusí zamknout hodnotu
po zamčení hodnoty provede potřebné operace a odemkne hodnotu

Sdílené a výhradní zámky (Víceúrovňové zámky)

Tyto zámky se dělí na dva druhy, podle toho, jestli zamykají čtení hodnoty, nebo zápis hodnoty:

read_lock(X): Více transakcí najednou může použít read_lock
- transakce NEMŮŽE použít read_lock(X), pokud jiná transakce použila write_lock(X)
write_lock(X): Pouze jediná transakce může použít write_lock
- transakce NEMŮŽE použít write_lock(X), pokud je hodnota X jakkoliv zamčená

Platí, že unlock(X) odemyká jak read_lock, tak write_lock nad touto hodnotou.

Postup aplikace víceúrovňových zámků:

Pro čtení:
- transakce se pokusí zamknout hodnotu, kterou chce číst, pokud jiná hodnota nepoužila write_lock
- pokud je hodnota write_locknutá, tak transakce čeká, než bude hodnota odemčena
- pokud hodnota není write_locknutá, transakce zvýší počítadlo, které určuje, kolik jiných transakcí read_locknulo hodnotu a provede čtení
Pro zápis:
- transakce se pokusí zamknout hodnotu, kterou chce zapsat, pokud jiná transakce nepoužila read NEBO write lock
- v opačném případě čeká na odemknutí hodnoty, poté manažer zámků aktivuje tuto čekající transakci
- transakce se pokusí opět o zamknutí hodnoty
Pro odemknutí:
- pokud transakce zamkla pomocí write_locku hodnotu, tak ji odemkne (stále platí, že transakce nemůže odemknout hodnotu, kterou nezamknula)
- čekající transakce ve frontě se aktivují
- pokud transakce odemyká svůj read_lock nad hodnotou, tak dekrementuje hodnotu počítadla
- pakliže je počítadlo na 0, nastaví se hodnota proměnné na unlocked a manažer zámků aktivuje transakci, jež čeká ve frontě

Transakce již nyní nejsou konkurentní, ale zároveň stále nejsou sériové. Jedná transakce si může hodnotu read_locknout, přečíst ji a unlocknout -> má ji přečtenou a je připravena s ní něco dělat. Jenže mezi unlocknutím a tím, než s tou hodnotou transakce něco udělá stihne jiná transakce tuto hodnotu také read_locknout, přečíst, unlocknout, provést operaci, write_locknout a zapsat (čímž zneplatní hodnotu, kterou předtím první transakce přečetla).


obr. 2: Nesériové zpracování i po aplikaci sdílených a výhradních zámků

Tento problém se řeší dvoufázovým zamykáním.

Dvoufázové zamykání

Jedná se o proces zamykání, kde se všechny operace zamykání provedou před jakoukoliv operací odemykání. Jde tedy o postupy aplikace sdílených a výhradních zámků.

Máme 3 druhy:

základní: všechny zamykací operace jsou časově před odemykacími operacemi
konzervativní: předem se stanoví hodnoty, které se mají zamknout - množina hodnot pro zápis a množina hodnot pro čtení
- pokud se nepodaří zamknout jednu položku z množiny, nezamkne se žádná
striktní: žádný zámek není uvolněn, pokud není transakce potvrzena (dokončena) - může způsobit deadlock

Řešení deadlocku - časové známky.

Časové známky (TimeStamp - TS)

Časová známka je proměnná, která je přidělena každé transakci. Tato proměnná se mění podle toho, jak transakce probíhá -> čítač.

Princip je uspořádat transakce podle nejvyšší hodnoty TS.

hodnota read_TS(X): obsahuje nejvyšší TS ze všech transakcí, které úspěšně četly X.
hodnota write_TS(X): obsahuje nejvyšší TS ze všech transakcí, které úspěšně zapsaly X

Kdykoliv transakce chce psát nebo zapisovat, tak algoritmus transakčního uspořádání porovná TS transakce s read_TS(X) nebo s write_TS(X) a kontroluje, zdali není narušené pořadí -> pokud je pořadí narušené, transakce musí počkat a začít znovu, nebo provést rollback.

Multiverze

Techniky multiverzního řízení:

pomocí časových značek
pomocí dvoufázového zamykání

Časové značky

Systém udržuje více verzí (proto mutliverze) hodnoty. Může to být $X1, X2, ..., X_n$.

každá položka $X_i$ma svojí hodnotu read_TS a write_TS
pokud se transakce snaží zapisovat nebo číst je vytvořená nová verze $X_i + 1$, jejíž časová známka je
- $read\_TS(X_i + 1)$ pokud chce číst
- $write\_TS(X_i + 1)$ pokud chce zapisovat

Postup aplikace:

Pro read:

Najde se verze $X_i$ s nejvyšší hodnotou write_TS pro tuto hodnotu (X), která odpovídá $X_i$.

Pro write:

Pokud má X nejvyšší hodnotu pro write_TS(X) takovou, že je menší nebo rovna TS(T) a současně je TS(T) menší než read_TS tohoto X, tak nastane rollback, v opačném případě se vytvoří nová verze X.

Timestamp hodnoty musí souhlasit s timestampem transakce, pokud tomu tak není, tak s touto hodnotou již operuje jiná transakce.

Zdroje

Transakce, řízení konkurenčních přístupů. https://docplayer.cz/4060766-10-transakce-rizeni-konkurencnich-pristupu.html

Vestavné systémy

Definice. Charakteristika vestavěných systémů. Použití v bankomatu, avionice, mobilní telefony, domácí automatizace, kalkulačky, zabezpečovací systémy, zdravotní přístroje, herní konzole apod.

Definice

Krátká

Kombinace hardwaru a softwaru, jejímž smyslem je řídit externí proces, zařízení nebo systém.

Zdroj: https://www.automa.cz/cz/casopis-clanky/vestavne-systemy-charakteristika-vyvoj-pouziti-2007_10_34242_3985/ (upraveno)

Dlouhá

Vestavěný systém (VS) je (většinou) jednoúčelový počítač, ve kterém je řídicí systém zcela zabudován do zařízení, které ovládá. Na rozdíl od univerzálních počítačů, jako jsou osobní počítače, jsou zabudované systémy většinou specializované, určené pro předem definované činnosti. Díky tomu jej tvůrci mohou při návrhu zjednodušit a optimalizovat, a tak snížit nároky na prostředky a cenu. Vestavěné systémy jsou často vyráběny sériově ve velkém množství, takže úspora bývá znásobena velkým počtem vyrobených kusů.

Zdroj: Přispěvatelé Wikipedie, Vestavěný systém [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 10. 03. 2023, 18:19 UTC, [citováno 4. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Vestav%C4%9Bn%C3%BD_syst%C3%A9m&oldid=22532985 (výrazně upraveno)

Charakteristika

Uvedené vlastnosti nemusejí být platné vždy pro každý VS. Ale obecně lze říci, že čím víc jich systém má, tím spíše se jedná o vestavěný systém.

Pokud se jedná o porovnání (např. menší výkon), vztahuje se k univerzálním počítačům (jako např. osobní počítače).

specializace pro konkrétní účel
přímo součástí většího zařízení, které řídí
bez interakce s člověkem (a tedy bez běžného rozhraní, jako displej, myš a klávesnice)
interakce se senzory, aktuátory a jinými VS
OS (obvykle platí jedna z možností):
- pracuje v reálném čase (RTOS)
- úplně chybí (běží pouze program)
vysoké nároky na spolehlivost (VS se často používají v kritických aplikacích (zdravotnictví, energetika, atd.); restart či oprava jsou obvykle velmi náročné nebo dokonce nemožné)
menší výkon (vyšší není nutný)
výrazně nižší spotřeba
menší rozměry
nižší cena

Použití

Kalkulačky

Kalkulačky jsou dobře známým a snadno pochopitelným příkladem vestavěných systémů. Mají jeden konkrétní účel, řídicí jednotka je integrována do zařízení, většinou neobsahují operační systém, výkon řídicí jednotky je minimální, ale vzhledem optimalizaci ke konkrétnímu danému účelu naprosto dostačující. Rovněž spotřeba a výrobní cena je velmi nízká.

Odchylkou od běžných charakteristik je rozhraní, které je uzpůsobené interakci s člověkem (displej, klávesnice).

Domácí automatizace

Domácí automatizace bývá často oblastí, kde dochází k prvnímu vědomému kontaktu s vestavěnými systémy. Ač existuje spousta hotových řešení (Home Assistant, SmartThings, Google Home, atd.), je zde mnoho prostoru a nízká vstupní bariéra pro DIY. Na internetu lze nalézt mnoho návodů na stavbu vlastních zařízení (vestavěných systémů), od malých a jednoduchých meteostanic po komplikované řídicí jednotky, komunikující bezdrátově s desítkami senzorů. Tato možnost získat pohled dovnitř světa vestavěných systémů (na rozdíl od toho vnějšího, konzumního), často vede k hlubšímu zájmu o tuto oblast, který může vyústit ve studium a následnou kariéru se zaměřením na vestavěné systémy.

Lze tedy říci, že oblast domácí automatizace má ve světě vestavěných systémů zvláštní místo, jako jakási vstupní brána.

Je nutné zmínit zde IoT (Internet of Things), což je koncept "pochytřování" obyčejných zařízení (přidávání senzorů a konektivity), který je v domácí automatizaci všudypřítomný. Lze říci, že domácí automatizace je podmnožinou IoT.

Z pohledu souladu s charakteristikami vestavěných systémů ja domácí automatizace poměrně složitá, jelikož zahrnuje celé spektrum rozličných zařízení. Vyjmenujeme si alespoň ta nejběžnější z nich:

"chytré" termostaty a ovladače proudění vzduchu
řídicí jednotky osvětlení
měřiče kvality ovzduší
meteostanice
domácí asistenty
energetické řídicí jednotky (např. k solárním panelům)
zabezpečovací systémy (viz níže)
pomocné roboty (např. vysavače)
"chytré" spotřebiče
řídicí jednotky zavlažování

Zabezpečovací systémy

Řídicí jednotky zabezpečovacích systémů jsou typickým příkladem vestavěných systémů, jelikož mají mnoho jejich charakteristických rysů. Jsou víceméně jednoúčelové, vestavěné do uzavřeného zařízení, komunikují se senzory (s člověkem jen přes řídicí rozhraní - typicky aplikace), HW není příliš výkonný, využívají vestavěné OS. Příkladem mohou být systémy od společnosti Jablotron.

Kromě řídicích jednotek lze za vestavěná zařízení často považovat i jejich periferie, jako např kamery, automatické zámky, či pohybová čidly. Ty totiž obvykle mívají vlastní řídicí vestavěný systém.

Mobilní telefony

Mobilní telefony jsou specifickým typem vestavěných systémů. Historicky do této kategorie právem spadaly (ač měly rozhraní pro komunikaci s člověkem, jednalo se o malá jednoúčelová zařízení - bezdrátová komunikace odkudkoliv). Dnes se však čím dál více přibližují univerzálním počítačům (univerzální použití, pokročilé OS i aplikace, vysoký výkon, cena i spotřeba, atd.).

Bankomaty

Řídící jednotky bankomatů jsou jedním z příkladů vestavěných systémů s vysokými požadavky na spolehlivost a bezpečnost (i když bezpečnost je nutno brát s velkou rezervou, viz níže). Jsou totiž velmi lákavým cílem útočníků. Rovněž není z pohledu uživatelů (bankovních klientů) přípustné, aby např. vlivem chyby v SW došlo k restartu aplikace nebo celého zařízení uprostřed úkonu (jako např. vklad hotovosti).

Z technického hlediska bankomaty kombinují rozhraní pro interakci s člověkem (displej, numerická klávesnice, čtečka karet, zařízení pro výdej bankovek, tiskárna stvrzenek) s klasickým (autonomním) rozhraním vestavěných systémů (senzor přítomnosti bankovek při výdeji, podávací mechanizmus pro bankovky, bezpečnostní systém). Co se týče SW, bankomaty, stejně jako většina bankovního sektoru, naprosto nepochopitelně používají zastaralé technologie plné zranitelností (v době ukončení rozšířené podpory Windows XP jej používalo 95% bankomatů na světě). Tyto problémy jsou kompenzovány vysokou fyzickou bezpečností zařízení.

Avionika

Avionika (elektronika užívaná v letectví) zahrnuje celou řadu vestavěných systémů:

komunikační zařízení - komunikace s řídicí věží, s pasažéry
navigátory - satelitní navigace (GPS, Galileo, WAAS), pozemní rádiová (VOR, LORAN), inerciální navigační systém (kombinace akcelerometrů a gyroskopů)
systémy kontroly letu - autopilot
palivová kontrola - Fuel Quantity Indication System (FQIS)
systémy vyhnutí kolizím - Traffic Collision Avoidance System (TCAS), vysílá signál, který zachytí tentýž systém v jiném letadle, ten pošle odpověď, oba informují pilota a navrhnou cestu pro vyhnutí
letové záznamníky - černé skříňky
monitory počasí - Weather Surveillance Radar, detektor blesků
monitory letadla - sledování vnitřních stavů letadla, životnosti komponent, atd.

Z pohledu SW je zajímavá především specifikace ARINC 653, která definuje parametry pro RTOSy používané v avionice.

Drony

Drony jsou samostatnou skupinou kombinující avioniku a robotiku, tedy dvě oblasti, ve kterých mají vestavěné systémy důležité místo.

Příklady vestavěných systémů (a jejich SW) pro drony:

Pixhawk - soubor otevřených standardů definujících HW vlastnosti vestavěných zařízení, aby byla zajištěna vzájemná interoperabilita (řídicí jednotky odpovídající standardu: Pixhawk 4, Auterion Skynode, atd.)
Paparazzi UAV - open-source HW a SW, který umožňuje autonomní činnost UAV (pochytřuje "hloupá" UAV)
Neousys Technology POC 200 (a další modely) - průmyslové minipočítače, používané v avionice a robotice (obvykle na nich běží OS pro univerzální počítače, ale používají se jako vestavěná zařízení)
ArduPilot - sada SW nástrojů pro tvorbu řídicích aplikací

Zdravotní přístroje

Vzhledem k tomu, že medicínská zařízení často stojí doslova mezi životem a smrtí, je zřejmé, že se jedná o kritické aplikace. Ty vyžadují tu nejvyšší spolehlivost, kterou poskytují právě (některé) vestavěné systémy. Konkrétně vestavěné systémy s RTOS, splňující přísné standardy (jako např. IEC 62304 pro SW). Jedná se např. o monitory tělesných funkcí, mimotělní oběhy, plicní ventilátory, atd. Některá z těchto zařízení bývají navíc bez možnosti opravy (např. kardiostimulátory).

Kromě těch nejkritičtějších zařízení obsahuje oblast zdravotnictví i další, která nevyžadují tak přísnou spolehlivost. Jedná se např. o měřiče tělesných vlastností pro běžné prohlídky. I tato zařízení obsahují vestavěné systémy, ty však obvykle nedosahují kvalit výše popsaných, což je ovšem vykoupeno nižší cenou.

Herní konzole

Herní konzole naplňují charakteristiky vestavěných systémů především z pohledu účelnosti (mají jen jeden), ceny a rozměrů. V ostatních charakteristikách se podobají spíše univerzálním počítačům:

PlayStation
- standardní PC HW (i když low-power varianty) - CPU a GPU od AMD
- OS modifikované FreeBSD (desktopový systém)
- rozhraní univerzální (USB, RJ-45, ...), ale obecně určené pro připojení periferií k interakci s člověkem
XBOX
- HW podobný jako PS
- OS modifikované Windows
- rozhraní podobné jako PS
Nintendo Switch
- nejvíce odpovídá vestavěným zařízením
- integruje rozhraní (biť pro komunikaci s člověkem) do jednoho zařízení spolu s řídicí jednotkou
- CPU a GPU od Nvidia (mobilní)
- OS proprietární (pravděpodobně ve stylu mobilních OS)

Zdroje

https://www.automa.cz/cz/casopis-clanky/vestavne-systemy-charakteristika-vyvoj-pouziti-2007_10_34242_3985/
Přispěvatelé Wikipedie, Vestavěný systém [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 10. 03. 2023, 18:19 UTC, [citováno 4. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Vestav%C4%9Bn%C3%BD_syst%C3%A9m&oldid=22532985
Wikipedia contributors, Home automation [online], Wikipedia, The Free Encyclopedia; 2023 May 4, 13:12 UTC [cited 2023 May 5]. Available from: https://en.wikipedia.org/w/index.php?title=Home_automation&oldid=1153142338
Přispěvatelé Wikipedie, Bankomat [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 6. 02. 2023, 11:29 UTC, [citováno 5. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Bankomat&oldid=22415962
Wikipedia contributors, Automated teller machine [online], Wikipedia, The Free Encyclopedia; 2023 Apr 10, 11:31 UTC [cited 2023 May 5]. Available from: https://en.wikipedia.org/w/index.php?title=Automated_teller_machine&oldid=1149134216
Wikipedia contributors, Avionics [online], Wikipedia, The Free Encyclopedia; 2023 Apr 28, 22:35 UTC [cited 2023 May 5]. Available from: https://en.wikipedia.org/w/index.php?title=Avionics&oldid=1152220489
Wikipedia contributors, Traffic collision avoidance system [online], Wikipedia, The Free Encyclopedia; 2023 May 2, 03:10 UTC [cited 2023 May 5]. Available from: https://en.wikipedia.org/w/index.php?title=Traffic_collision_avoidance_system&oldid=1152755626
https://www.playstation.com/cs-cz/ps4/tech-specs/
Wikipedia contributors, PlayStation [online], Wikipedia, The Free Encyclopedia; 2023 Apr 29, 18:24 UTC [cited 2023 May 6]. Available from: https://en.wikipedia.org/w/index.php?title=PlayStation&oldid=1152351658
Wikipedia contributors, Xbox system software [online], Wikipedia, The Free Encyclopedia; 2023 May 2, 21:53 UTC [cited 2023 May 6]. Available from: https://en.wikipedia.org/w/index.php?title=Xbox_system_software&oldid=1152883026
https://www.cnews.cz/microsoft-xbox-series-x-specifikace
Wikipedia contributors, Nintendo Switch system software [online], Wikipedia, The Free Encyclopedia; 2023 Apr 22, 01:25 UTC [cited 2023 May 6]. Available from: https://en.wikipedia.org/w/index.php?title=Nintendo_Switch_system_software&oldid=1151116659
https://www.nintendo.com/switch/tech-specs/
https://pixhawk.org/
https://wiki.paparazziuav.org/wiki/General
https://www.neousys-tech.com/en/product/product-lines/industrial-computers
https://ardupilot.org/ardupilot/index.html
https://www.wikiskripta.eu/w/Kardiostimul%C3%A1tor

Architektura mikrokontrolérů pro vestavné systémy

rozdělení mikrokontrolerů (dvě hlavní architektury - von Neumannova, Harvardská architektura, podle souboru instrukcí - CISC, RISC, DSP), paměti ve vestavných systémech (s libovolným přístupem, se sekvenčním přístupem, semipermanentní paměť)

V dnešní době existuje několik typů/rodin mikrokontrolérů které se používají v embedded systémech, uvedeme si ty nejvíce používané společně se základními parametry a příklady vývojových desek, na kterých se používají.

Mikrokontrolér vs Mikropočítač

mikrokontrolér je CPU společně s registry a řadiči + základní periferie
mikropočítač je vývojová deska na které se nachází mikrokontrolér společně s dalšími periferiemi

Základní používané mikrokontroléry:

PIC
- používá RISC instrukce (RISC architektura) -> lepší modely mají přidané DSP instrukce
- jedná se o Harvardskou architekturu
- klasicky je 16 - bitový, dělají se i 32 - bitové verze
- obsahuje JTAG sběrnici
- používá se v samostatných embedded systémech jako jsou například alarmy, telefony nebo senzorika (jsou velmi malé)
- základní adresní módy (přímý, nepřímý, relativní)
ARM
- používá RISC instrukční sadu
- umožňuje velké množství adresních módů
- mají menší spotřebu el. energie
- v základu 32 bitová architektura (může být i 64 bitová)
- v embedded systémech se tyto procesory využívají převážně v telefonech, televizích, nebo GPS navigacích
8051
- používá lehce upravenou CISC instrukční sadu
- je 8 bitový s 16 bitovou adresní sběrnicí
- jedná se o Harvardskou architekturu
- jeho využití je pro základní aplikace, které nejsou paměťově náročné -> hodí se pro výukové účely
AVR
- používá upravenou RISC sadu instrukcí -> Advanced Virtual RISC
- jedná se o Harvardskou architekturu
- dělí se na 3 kategorie:
  - TinyAVR (ATtiny): malá paměť, zabírá málo místa (fyzicky), hodí se pro jednoduché úkony
  - MegaAVR (ATmega): nejpoužívanější, dostatečná paměť, velké množství zabudovaných periferií
  - XMegaAVR: používaný komerčně pro komplexní projekty, kde je potřeba velká paměť a rychlost
- podporuje proudové zpracování instrukcí
MSP
- 16 bitový
- RISC architektura
- malá spotřeba, malá velikost -> stejně jako všechny ostatní

Instrukční soubor

Instrukční soubory RISC a CISC jso u popsaný v otázce Instrukční soubor.

DSP (Digital SignaL Processing)

Jedná se procesory, které jsou optimalizované pro pro zpracování signálu. Tyto procesory používají speciální sadu instrukcí -> DSP instrukcí. Tyto procesory nepodporují přerušení. Používají nestandardní paměť a jsou tím pádem obtížnější na programování.

Platí, že:

pokud chceme zpracovávat zvuk, video, rychle řídit motory, nebo cokoliv co vyžaduje zpracovávání proudu dat velkou rychlostí, tak použijeme DSP procesor
pokud chceme kontrolovat tlačítka, měřit teplotu nebo ovládat LCD display, použijeme klasický mikrokontrolér DSP slouží ke zpracování signálu tím, že signál se převede na digitální, zpracuje se a převede se opět na analogový


obr. 1: Princip fungování DSP
zdroj: https://en.wikipedia.org/wiki/Digital_signal_processor#/media/File:DSP_block_diagram.svg

Paměti

Máme 3 druhy pamětí:

paměť s libovolným přístupem: RAM, rychlost získání dat nezávisí na tom, kde jsou data v paměti uložena. Používá řadič paměti k nalezení buňky s daty na základě adresy poskytnuté procesorem.
paměť se sekvenčním přístupem: Paměť lze přečíst jen postupně, například posuvný registr, nebo paměti typu FIFO/LIFO. Magnetická páska je příklad paměti se sekvenčním přístupem.
semipermanentní paměť: Jedná se o nevolatilní druh paměti. Tato paměť si udržuje v ní uložené hodnoty i bez nutnosti stále připojení k elektrické síti. Dřívější druhy těchto pamětí nemohli byt vymazány bez toho, aniž by byl nutná fyzický zásah (vyjmutí paměti, posvícení UV světlem v případě EPROM).
- Dnes se využívá EEPROM -> elektricky vymazatelná paměť pouze pro čtení. Tato paměť dokáže i zapisovat a klasicky vydrží přes 200 tisíc zápisů. V embedded zařízeních je tento druh paměti využit k uchování dat po odpojení zařízené od elektrické sítě.
- Princip spočívá v tom, že každá paměťová buňka se skládá z tranzistorů NMOS. Je složena ze dvou vrstev, jedna je z nitridu křemíku a druhá z oxidu křemičitého. Mezi těmito vrstvami je náboj uložen.
- Při zápisu se přivede na příslušný adresový vodič (buňku) záporné napětí a datový vodič buňky se uzemní. Tranzistor se otevře a vznikne v něm prahové napětí.
- Při čtení se přivede na adresový vodič záporný impuls. Tranzistor s malým prahovým napětím se otevře a vyvede proud na datový vodič. V případě velkého prahového napětí zůstává otevřen.
- Dalším druhem paměti je Flash paměť. Je také nevolatilní, ale na rozdíl od EEPROM je rozdělena do jednotlivých sekcí, které lze zvlášť mazat. Tento druh paměti (resp. jeho NAND varianta) je využíván v SSD.

Více o těchto druzích pamětí se lze dočíst v otázce Paměťový podsystém počítače.

Zdroje

Architektura operačních systémů užívaných ve vestavných systémech

Linux, Android, iOS, AppleTV, apod. Operační systémy pracujícím v reálném čase (RTOS), ROS (Robotický operační systém).

Linux

Linux je svobodný (pod licencí GNU GPLv2) operační systém původně vytvořený pro architekturu IA-32 (známá též jako i386 (podle prvního procesoru této architektury - Intel 80386)). Časem byla přidána podpora dalších architektur (x86-64 - současné PC; ARM, RISC-V - embedded zařízení; atd.). Návrh systému vychází z UNIXu a dodržuje příslušné standardy POSIX a SUS (Single UNIX Specification). Je naprogramován (myslíme zde jádro) v jazyce C a od verze 6.1 i Rust (zatím jen pro ovladače).

Názvosloví

Označení Linux původně znamenalo pouze jádro (kernel), poměrně rychle se však vžilo i pro systém jako celek (včetně aplikací atd.) a dnes se tak používá primárně. Z toho později vznikla kontroverze Linux vs GNU/Linux. Zde uvedený popis se vztahuje primárně k jádru, ale jze jej přeneseně použít pro celý systém.

Kromě označení Linux se často používá i linuxová distribuce - to znamená linuxové jádro spolu s aplikacemi, které dohromady tvoří funkční systém, připravený k použití rovnou po instalaci (zde tedy záleží na parametrech konkrétní distribuce, některé je třeba před použitím ještě doupravit, ale základní systém obsahují stejně).

Architektura

Na architekturu vestavěného Linuxu lze hledět v různých úrovních abstrakce. Zde si uvedeme ty nejvyšší z nich. Nutno dodat, že v těchto úrovních se architektura vestavěného Linuxu prakticky neliší od architektury standardního linuxu. Rovněž je třeba zmínit, že zde myslíme Linux jako celý systém, nikoliv pouze jádro.

Základní vrstvy architektury jsou tyto:

zavaděč (není přímo vrstvou, viz níže)
kernel
knihovny
služby
uživatelské aplikace

Zavaděč

Zavaděč (anglicky bootloader) je program, jehož úkolem je po startu zařízení zavést operační systém. Na osobních počítačích se nejčastěji setkáme se zavaděči GRUB (Linux) a WBM (Windows). Ty nabízejí celou řadu funkcí, které však v embedded světě nevyužijeme (např. grafické rozhraní, automatický výběr paměti pro zavedení v základním nastavení, atd.), proto se zde využívají zavaděče s minimálními nároky, uzpůsobené pro potřeby vestavěných systémů, jako např. Das U-Boot. Tyto zavaděče obecně poskytují v základním nastavení pokročilou funkcionalitu, kterou naopak nevyužije běžný uživatel na osobním systému (např. možnost zadávat přímo parametry kernelu). Krom toho mají podporu pro větší množství ve vestavěných systémech běžného HW.

Kernel

Kernel, neboli jádro je hlavní část systému. Jeho úkolem je řízení přidělování prostředků (paměťový prostor, procesorový čas) a obsluha I/O zařízení. Linuxový kernel je co se týče návrhu modulární a monolitický, to znamená, že umožňuje načítání externích modulů (modulární) a že zde není přístupová ochrana mezi jeho jednotlivými subsystémy, které mohou volat vzájemně své funkce (monolitický). Lze jej dělit na další součásti, viz obr. 1.


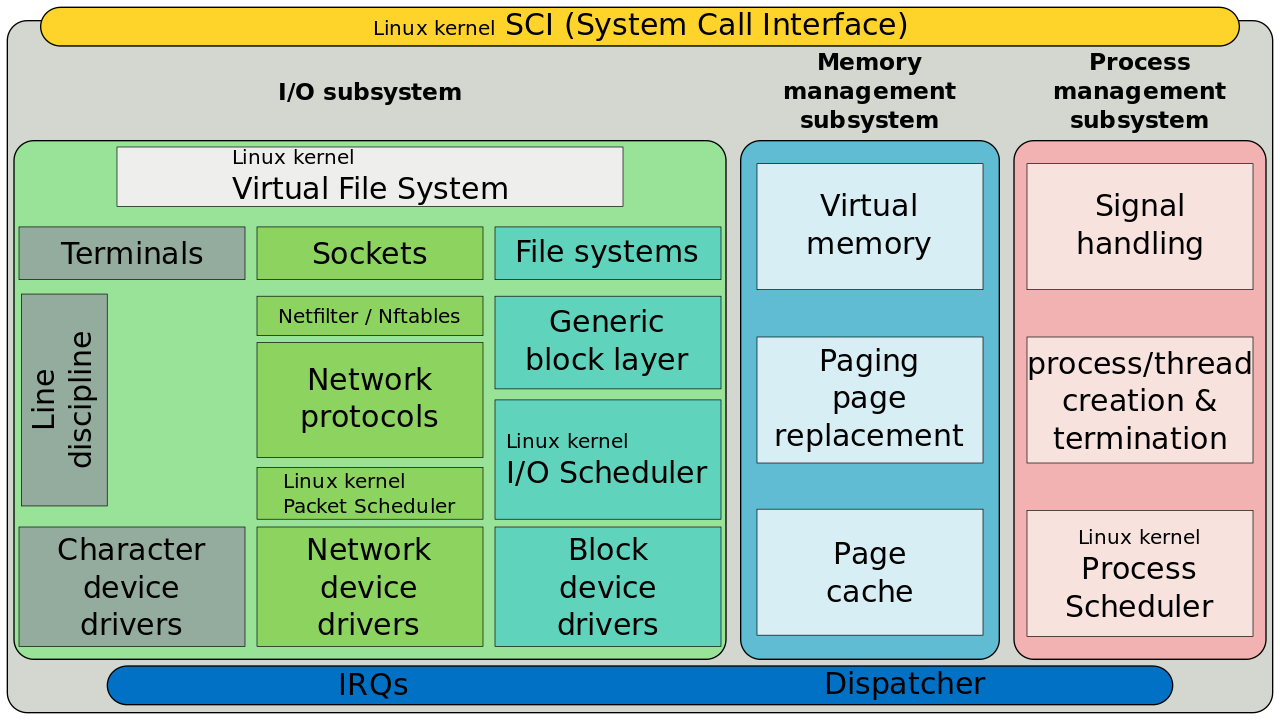obr. 1: Struktura linuxového kernelu
zdroj: ScotXW, CC BY-SA 4.0, via Wikimedia Commons

IRQ

IRQ (Interrupt ReQuest) je systém přerušení, která mohou po jádru požadovat externí zařízení. Každé přerušení má své číslo, podle kterého jádro určuje zdroj přerušení. Při detekci přerušení zavolá jádro obslužnou rutinu (funkci).

Dispatcher

Určuje, který proces se má stát aktivním (může vykonávat svou činnost, přistupovat k prostředkům, atd.).

I/O subsystem

I/O subsystem obsluhuje vstupně výstupní zařízení. Obsahuje ovladače, implementace protokolů a další komponenty, které jsou pro tuto obsluhu nutné. Má tři hlavní součásti:

terminál - rozhraní pro použití terminálových emulátorů
síť - ovladače, protokoly, sockety a celkově infrastruktura pro práci se sítí
úložiště - ovladače, souborové systémy a další prvky pro abstrakci práce s fyzickým úložištěm

Rovněž sem patří ovladače pro všechna periferní zařízení (možná spadají pod kategorii úložiště, jelikož v Linuxu platí že všechno je soubor, a tedy přístup k těmto zařízením funguje stejně jako k úložišti)

Memory management subsystem

Stará se o přidělování a obecnou správu paměti. Detailně popsáno v kapitolách 2.3.1, 2.3.2 a 2.3.3.

Process management subsystem

Řídí životní cyklu procesů, jejich komunikaci a řazení pro přístup k prostředkům. Detailně popsáno v kapitolách 2.3.1 a 2.3.4.

SCI

SCI (System Call Interface) je API jádra, skrze které mohou programy běžící v user space přistupovat k prostředkům jádra (tedy ke kernel space), či mu zasílat požadavky. Zajišťuje bezpečnost (aby programy nemohly přistupovat tam, kam nemají = přímo do kernel space).

Kernel & user space

Jedná se o rozdělení prostoru virtuální paměti na dvě části, za účelem zvýšení bezpečnosti.

kernel space - prostor, kam můžou přistupovat pouze služby jádra (plánovač, správce paměti, atd.)
user space - sem mohou přistupovat uživatelské aplikace a další přídavné moduly, které nejsou přímo součástí jádra (detailně popsáno v sekci RTOS - mikrokernel)

Knihovny

Jedná se o knihovny, které lze využít při tvorbě uživatelských aplikací, pro přístup k prostředkům jádra a komunikaci s ním. Nejdůležitější z nich je standardní knihovna jazyka C (na klasických PC je to obvykle glib, na vestavěných např. uClibc).

Služby

Službami se myslí programy, které běží na pozadí a starají se o důležité části systému, které už však leží v user space (nejsou součástí jádra). Nejdůležitější službou je init system, což je první proces, který jádro spustí hned po svém zavedení. Jeho úkolem je spouštění dalších procesů. Na běžných PC se téměř výhradně užívá systemd, na vestavěných např. OpenRC, sninit.

Uživatelské aplikace

Sem spadá zbytek aplikací z user space. Jedná se o aplikace, které uživatel spouští cíleně, aby s nimi pracoval. U vestavěných systémů to obvykle bývá konkrétní řídicí program (nebo soustava spolupracujících programů) pro ovládání systému.

Obecné rozdíly mezi klasickým a vestavěným Linuxem

Vzhledem k tomu, že vestavěné systémy mají obecně méně zdrojů (RAM, výkon procesoru, atd.), je snahou co nejvíce omezit nároky systému. Toho se dociluje odstraněním nepotřebných aplikací (např. grafické prostředí a X (grafický) server, aplikace přímo pro uživatele, atd.), použitím menší sady základních utilit (základní utility jsou např. ls, cp, rm, atd.) či kompaktnější implementace standardní C knihovny (místo glibc např. uClibc) nebo úpravou jádra pro běh v reálném čase (RTOS). Vzhledem k tomu, že vestavěné systémy mají obvykle jedno specifické užití a předem známý HW, není u nich nutná variabilita ovladačů, a proto je možné nepotřebné odebrat.

Výhody a nevýhody použití vestavěného Linuxu (oproti jiným vestavěným OS)

Výhody

podpora široké škály HW
takřka neomezená možnost úpravy - přizpůsobení pro konkrétní řešení (v rámci podmínek GNU GPLv2)
nulové licenční poplatky
podpora není omezena na konkrétního dodavatele (možnost výběru)
vysoká stabilita

Nevýhody

vyšší náročnost na zdroje oproti klasickým RTOSům a podobným jednoduchým systémům

Vestavěné distribuce

Mobian - pro mobilní telefony
Ubuntu Touch - pro mobilní telefony
Real-Time Linux - linuxový RTOS
OpenWrt - pro síťové prvky
E2 Linux - pro set-top boxy a IPTV přijímače
webOS - pro mobilní zařízení (původně mobilní telefony, dnes hlavně chytré televize LG)
Raspberry Pi OS - prakticky plnohodnotný OS (s grafickým rozhraním a programy pro běžné uživatele), který běží na jednodeskových počítačích (které lze použít ve vestavěných zařízeních)

Platformy

OpenEmbedded - platforma (framework) pro automatické sestavování a překlad distribucí pro vestavěná zařízení
Yocto Project - tvorba procesů a nástrojů pro stavbu vestavěných distribucí, nezávislých na konkrétní HW platformě
ELKS (Embeddable Linux Kernel Subset) - zmenšené jádro pro použití ve VS

Android

Android je mobilní operační systém vyvíjený společností Google (skrze konsorcium Open Handset Alliance). Využívá upravené Linuxové jádro. Je vyvíjen jako Android Open Source Project (AOSP), který si výrobci upravují pro svá zařízení.

Z pohledu vestavěných zařízení jsou primárním cílem mobilní telefony a tablety (což nejsou vestavěná zařízení v pravém slova smyslu), nejedná se tedy o úplně klasický vestavěný OS. Nicméně má své místo u vestavěných systémů, které vyžadují grafický výstup, jako jsou např. reklamní kiosky a informační zařízení v automobilech (existuje upravená verze pro televize - Android TV). Krom toho existují upravené verze androidu, které na vestavěné systémy cílí přímo a umožňují relativně snadnou úpravu pro požadované řešení, jako např. emteria.OS. Existovala i jedna přímo od Googlu, ta však byla zrušena (jak je u Googlu dobrým zvykem). Tvorba vlastní vestavěné distribuce Androidu (přímo z AOSP) je podle všeho velmi náročná.

Architektura Androidu obecně

Vzhledem k tomu, že distribucí Androidu přímo určených pro vestavěná zařízení není mnoho a jsou obvykle proprietární, není jejich architektura veřejně dostupná. Dá se však předpokládat, že bude podobná té obecné a tak si zde popíšeme tuto.

Struktura architektury je následující (jdeme od HW směrem k uživatelským aplikacím):

Linux kernel
HAL
Nativní C/C++ knihovny & Android runtime
Java API framework
Systémové a uživatelské aplikace

Linux kernel

Je detailně popsán v části Linux.

HAL

HAL (Hardware Abstraction Layer) je zde API, skrze které může Java API framework přistupovat k HW prostředkům systému. Nejedená se o HAL v klasickém slova smyslu, protože "leží" nad linuxovým jádrem a tedy provádí abstrakci nad ním, nikoliv přímo nad HW.

Nativní C/C++ knihovny & Android runtime

Tyto dvě vrstvy leží na stejné úrovni proto jsou uvedeny dohromady.

Nativní C/C++ knihovny

Části systému, jako HAL a ART jsou napsány v C/C++ a tedy využívají nativní knihovny. Některé z jejich funkcionalit lze využít přímo při vývoji vlastních aplikací, skrze Java API framework. Rovněž je zde Android NDK, který umožňuje práci s těmito knihovnami přímo v C/C++ kódu.

Android runtime

Je to alternativa JRE (Java Runtime Environment), která funguje od Android 5. Každá aplikace na Androidu běží ve vlastním procesu a má vlastní instanci Android runtimu (ART). Aplikace jsou pro běh překládány do bytekódu DEX (ten je optimalizovaný pro běh na zařízeních s malou pamětí), který ART spouští.

ART umí:

ahead-of-time (AOT) a just-in-time (JIT) kompilaci
optimalizovaný garbage collection (GC)
překlad DEX kódu do menšího machine kódu (od Android 9)
podporu pro různé debug nástroje
obsahuje důležité Java knihovny, které obsahují většinu funkcionality Java 8

Java API framework

Je hlavní rozhraní, které slouží k vývoji aplikací. Funguje jako kompletní ekosystém. Nabízí např. následující funkcionalitu:

systém tzv. "Views" - tedy komponent, ze kterých lze skládat UI aplikace a které lze upravovat a vytvářet vlastní
správce notifikací - umožňuje zobrazovat notifikace uživateli
správce aktivit - řeší navigaci v aplikaci (přepínání mezi obrazovkami)
poskytovatel obsahu - umožňuje přístup k datům jiných aplikací
správce zdrojů (resources) - umožňuje pracovat se soubory, které nejsou zdrojový kód

Systémové a uživatelské aplikace

Všechny aplikace využívají Java API framework. Systémové aplikace jsou ty, které jsou předinstalovány v systému (Kontakty, Kalkulačka, atd.). Většinu z nich lze nahradit uživatelskými (s pár výjimkami, např. Nastavení).

Výhody a nevýhody použití Androidu (oproti jiným vestavěným OS)

Výhody

známý a poměrně odladěný ekosystém pro vývoj aplikací
připravené grafické prostředí

Nevýhody

velmi náročná (nebo drahá) úprava pro vlastní řešení
ekosystém není plně otevřený
vysoké nároky na prostředky

iOS

Jedná se o proprietární operační systém od firmy Apple. Z pohledu vestavěných systémů je použitelný pouze jako mobilní OS. Nelze jej totiž použít jinde než na mobilních telefonech a tabletech od firmy Apple (tedy ARMv7 a ARMv8). Je to odlehčená verze desktopového macOS (jedná se tedy o OS UNIXového typu).

Architektura iOS

Architektura systému iOS je vrstvená. Obsahuje čtyři vrstvy, viz obr. 2.


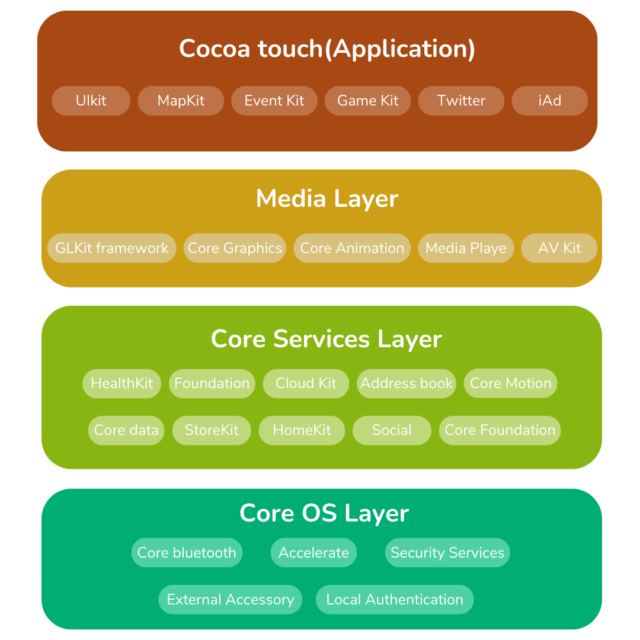obr. 2: Architektura iOS
zdroj: https://redfoxsec.com/blog/ios-architecture/

Core OS

Jedná se o jádro systému. Jeho funkce přibližně odpovídají jádru Linuxu.

Core Services

Vrstva abstrakce nad jádrem. Obsahuje služby, které jsou využívány vyššími vrstvami, jako např. správy účtů, volání, identifikátorů pro reklamu, nákupů v AppStore, atd.

Media Layer

Slouží k práci s audiem, videem a grafikou, a to jak v rámci systému samotného, tak pro vývojáře k užití při vývoji aplikací.

Cocoa Touch

Obsahuje obecné nástroje pro vývoj aplikací (UI prvky, zpracování událostí, notifikace, atd.). Odpovídá vrstvě Java API framework u Androidu.

Výhody a nevýhody použití iOS (oproti jiným vestavěným OS)

Výhody

poměrně jednoduchý vývoj, díky vysokoúrovňovým nástrojům (Swift, Xcode)

Nevýhody

prakticky se nejedná o vestavěný systém, nelze ho tedy téměř porovnat
pouze jedna platforma
pro vývoj je třeba konkrétní SW (Xcode), který běží jen na OS od firmy Apple, které běží zase jen na extrémně předraženém HW rovněž od firmy Apple
kompletně uzavřený ekosystém

AppleTV

V zařízeních Apple TV se užívá operační systém tvOS. Ten byl původně založen na macOS, ale nyní na iOS, ze kterého přebírá velkou část funkcionality a dalších vlastností (je to uzavřený systém, pro jeden typ zařízení, atd.).

O architektuře tvOS se bohužel nikde nic nepíše, ale lze odhadovat, že je podobná té z iOS.

RTOS

Definice z Wikipedie:

Pokud lze dokázat, že realtime systém splní svá ultimáta (deadlines) (a to za použití chování systému v nejhorším možném případě, nikoliv analýzou průměrného chování systému), potom můžeme říci, že chování systému je předvídatelné.

RTOS (Real Time Operating System) se od klasických operačních systémů liší principem činnosti plánovače (scheduleru). V běžném OS (jako např. Linux) je jeho cílem přepínat procesy tak, aby všichni uživatelé systému dostávali podobný čas a aby se jim běh systému zdál plynulý. Ve vestavěných systémech obvykle nemáme více uživatelů (často vůbec nemáme koncept uživatele) a mnohem více nás zajímá předvídatelnost systému.

Často jsou vyžadovány požadavky reálného času (real time requirements), což znamená, že systém musí vykonat nějakou činnost v definovaném čase (deadline). Aby bylo možno tyto požadavky naplnit, systém musí být deterministický, tedy musí mít předvídatelné plánování (scheduling).

Determinismu při multitaskingu se u RTOSů obvykle dosahuje pomocí priorit, které se přidělují jednotlivým vláknům (nazývaným task). Na základě těchto priorit určuje plánovač, které vlákno bude v činnosti jako následující.

Základní požadavky na RTOS jsou:

preemptivní plánovač - právě vykonávanou úlohu může přerušit bez její asistence
přesné hodiny reálného času
velký počet priorit, které lze nastavit vláknům

Základní požadavky na plánovač RTOSu jsou:

minimální latence při reakci na událost
minimální latence při přepínání vláken
minimalizace časových okamžiků, kdy je zakázáno přerušení

RTOSy lze delit na dva druhy:

hard RTOS - vyžaduje striktní determinismus, tedy vykonání požadavku v konkrétním čase je naprosto nutné; používá se v kritických systémech
soft RTOS - povoluje drobné odchylky

Příklady používaných algoritmů pro plánování:

Rate monotonic scheduling (RMS) - priority se přidělují staticky; vyžaduje periodické úlohy
Earliest deadline first (EDF) - zpracování úloh probíhá na základě mezní doby platnosti procesu; nevyžaduje periodické úlohy

Architektura RTOS

Hlavní částí architektury RTOSu je kernel. Ten obsahuje podobné části jako např. linuxový kernel, tedy správu paměti, přidělování procesorového času, komunikaci a synchronizaci mezi procesy, obsluhu přerušení a obsluhu I/O zařízení. Rozdílem je, že neobsahuje souborový systém, síťové protokoly a ovladače zařízení. Tyto a další komponenty (např. terminál a nástroje pro debug) jsou vytvořeny jako samostatné moduly, které lze přidávat a odebírat podle potřeby konkrétního řešení (často se používá kernel samotný).

RTOSové kernely jsou ve většině případů tvz. mikrokernely. To znamená, že v kernel space běží jen minimum kódu (komunikace mezi procesy, správa paměti, přidělování prostředků, atd.), a zbylé služby (souborový systém, obsluha sítě, atd.) běží v user space (to odpovídá popisu výše). Kromě toho jsou také user space moduly od sebe odděleny a komunikují spolu skrze kernel space část. To zvyšuje bezpečnost a odolnost systému (když padne jeden modul, neshodí celé jádro), ale za cenu snížení výkonu.

Uživatelské aplikace mohou běžet přímo nad kernelem (u jednodušších aplikací je kernel to jediné, co aplikace potřebuje). Pokud aplikace pro svou činnost vyžaduje využití funkcionality některého z dalších modulů, lze jej jednoduše přidat.

Výhody a nevýhody použití RTOS (oproti jiným vestavěným OS)

Porovnání je opět problematické, jelikož se nejedná o jeden konkrétní OS, ale o typ. K porovnání tedy zvolíme FreeRTOS.

Výhody

mnohem menší nároky na prostředky
vhodný pro kritické aplikace
otevřený (neplatí pro RTOSy obecně)
mnoho podporovaných platforem
nevyžaduje přítomnost MMU (jednotka správy paměti - součást procesorů; řeší např. stránkování)

Nevýhody

obecně se nehodí pro aplikace, které přímo interagují s člověkem (např. informační kiosky)

ROS

ROS (Robot Operating System) je otevřený (licencovaný pod BSD licencí) soubor frameworků pro vývoj SW k řízení robotických systémů. Nejedná se tedy přímo o OS, ale o nástavbu nad ním. Lze jej použít nad Linuxem, Windows a macOS.

Architektura ROS

ROS je navržen jako middleware, který propojuje jednotlivé "mini aplikace" (nazývané procesy) a umožňuje jim vzájemně komunikovat. Procesy fungují jako uzly grafu, kde hrany jsou reprezentovány tématy (topic), skrz které si mohou procesy posílat zprávy, nabízet a konzumovat služby, či přistupovat do společné databáze.

Před zahájením komunikace se musejí procesy zaregistrovat u centrálního procesu, nazývaného ROS Master. Ten mezi nimi vytvoří peer-to-peer spojení, skrze které následně komunikují (jedná se tedy o distribuovaný systém).

Komunikace skrze témata funguje na principu publish-subscribe. Tedy jeden proces provede subscribe (odběr) na nějaké téma a čeká na zprávu, kterou na dané téma publikuje (publish) jiný proces. Formát takto posílaných zpráv je čistě v režii uživatele.

Výše zmíněné služby fungují jako jednorázové akce, které přímo nabízí proces ostatním (např. získání snímku z kamery).

Společná databáze (parameter server) slouží k ukládání málo se měnících dat, která jsou potřebná pro větší množství procesů (např. hmotnost robotu).

Kromě této základní struktury ROS obsahuje velkou sadu nástrojů, které lze využít při tvorbě procesů. Jedná se např. o nástroje na vizualizaci (rviz), vylepšené logování (rosbag), build systém (catkin), konfigurace a spouštění procesů (roslaunch). Kromě toho také obsahu správce balíčku, který obsahuje nepřeberné množství knihoven pro řešení problémů nejen z oblastni robotiky.

Výhody a nevýhody použití ROS (oproti jiným vestavěným OS)

Výhody

mnoho nástrojů
poměrně snadná tvorba vlastních procesů
otevřený ekosystém
odladěný pro oblast robotiky

Nevýhody

běží jako nadstavba standardních OS, a tedy pouze tam, kde běží ony (verze 2 rozšiřuje podporu na běžnější vestavěná zařízení)

Zdroje

Linux

Přispěvatelé Wikipedie, Linux (jádro) [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 25. 04. 2023, 16:43 UTC, [citováno 1. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Linux_(j%C3%A1dro)&oldid=22737469
Přispěvatelé Wikipedie, Linux [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 9. 04. 2023, 15:34 UTC, [citováno 1. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Linux&oldid=22646583
Přispěvatelé Wikipedie, Vestavěný Linux [online], Wikipedie: Otevřená encyklopedie, c2020, Datum poslední revize 24. 10. 2020, 13:40 UTC, [citováno 1. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Vestav%C4%9Bn%C3%BD_Linux&oldid=19101906
http://etutorials.org/Linux+systems/embedded+linux+systems/Chapter+2.+Basic+Concepts/2.4+Generic+Architecture+of+an+Embedded+Linux+System/
https://www.eeweb.com/embedded-linux-design-kernel-analysis/
https://thenewstack.io/the-major-components-of-an-embedded-linux-system/
Wikipedia contributors, Bootloader [online], Wikipedia, The Free Encyclopedia; 2023 Jan 1, 12:02 UTC [cited 2023 May 2]. Available from: https://en.wikipedia.org/w/index.php?title=Bootloader&oldid=1130875419.
Přispěvatelé Wikipedie, Jádro operačního systému [online], Wikipedie: Otevřená encyklopedie, c2021, Datum poslední revize 23. 07. 2021, 22:12 UTC, [citováno 2. 05. 2023] https://cs.wikipedia.org/w/index.php?title=J%C3%A1dro_opera%C4%8Dn%C3%ADho_syst%C3%A9mu&oldid=20236887
https://linux-kernel-labs.github.io/refs/heads/master/lectures/intro.html
https://tldp.org/LDP/sag/html/init-process.html

Android

https://emteria.com/blog/embedded-android
https://developer.android.com/guide/platform
Přispěvatelé Wikipedie, Android (operační systém) [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 9. 04. 2023, 16:35 UTC, [citováno 2. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Android_(opera%C4%8Dn%C3%AD_syst%C3%A9m)&oldid=22646852

iOS

Wikipedia contributors, IOS [online], Wikipedia, The Free Encyclopedia; 2023 Apr 25, 11:49 UTC [cited 2023 May 2]. Available from: https://en.wikipedia.org/w/index.php?title=IOS&oldid=1151657740
https://redfoxsec.com/blog/ios-architecture/
Přispěvatelé Wikipedie, IOS [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 9. 04. 2023, 15:37 UTC, [citováno 3. 05. 2023] https://cs.wikipedia.org/w/index.php?title=IOS&oldid=22646601

AppleTV

Wikipedia contributors, TvOS [online], Wikipedia, The Free Encyclopedia; 2023 May 2, 21:15 UTC [cited 2023 May 3]. Available from: https://en.wikipedia.org/w/index.php?title=TvOS&oldid=1152877912

RTOS

https://www.freertos.org/about-RTOS.html
Přispěvatelé Wikipedie, Operační systém reálného času [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 18. 11. 2022, 16:57 UTC, [citováno 3. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Opera%C4%8Dn%C3%AD_syst%C3%A9m_re%C3%A1ln%C3%A9ho_%C4%8Dasu&oldid=21906385
https://robocraze.com/blogs/post/architecture-of-rtos-part-1
https://linux-kernel-labs.github.io/refs/heads/master/lectures/intro.html

ROS

https://www.ros.org/blog/why-ros/
Wikipedia contributors, Robot Operating System [online], Wikipedia, The Free Encyclopedia; 2023 May 2, 10:25 UTC [cited 2023 May 3]. Available from: https://en.wikipedia.org/w/index.php?title=Robot_Operating_System&oldid=1152793296

Architektura softwaru VS bez operačních systémů

Použit SW i HW INTERRUPTů, cyklické čtení periferii, softwarové řešení připojení pomalých a rychlých periferii (sofistikované displaye, kamery, joystick apod.)

Návrh architektury SW pro vestavěné systémy se dosti liší od návrhu architektury pro běžné aplikace. Standardní SW architektury upřednostňují modularitu, škálovatelnost a oddělenost celků na úkor efektivity daného řešení. U vestavěných systémů je však efektivita často jedním z nejdůležitějších aspektů (což ovšem neznamená, že výše zmíněné aspekty nehrají roli).

Rovněž běžné architektonické vzory (MVC, MVP, MVVM, ...) cílí na aplikace, se kterými interaguje uživatel, což se však u vestavěných systémů mnohdy neděje.

U vestavěných systémů nejsou přesně stanovené architektonické vzory, avšak jisté aspekty se objevují u většiny řešení:

oddělení vrstev
- interakce s HW bývá oddělena od aplikace samotné (většinou se mezi nimi nachází API)
- to umožňuje značné zpřehlednění aplikace s minimálním snížením efektivity
modularizace
- související části aplikace jsou spojeny do modulů
- dosti se protíná s běžnými aplikacemi
- je zde však kladen důraz na maximální zachování efektivity
- bývá důležitá, pokud je nutná bezpečnost (oddělení chráněných bloků od těch, které nesou rizika)
zaměření na datové pohyby
- při řešení struktury se bere v potaz tok dat systémem

Zde jsme si zběžně popsali architekturu SW VS z hlediska návrhu a struktury, níže se však budeme věnovat spíše konkrétním principům a technikám, které se při psaní vestavěného SW užívají.

SW a HW interrupt

Interrupt (neboli přerušení) je metoda, která umožňuje (obvykle) asynchronní zásahy do běžné činnosti zařízení. Spočívá v tom, že na základě nějakého popudu dojde k vyvolání obslužné rutiny (ISR). To nám umožňuje např. reagovat na stisk tlačítka nebo zařízením samotným si vzájemně posílat příkazy.

HW interrupt

HW interrupty (někdy též vnější interrupty) vyvolává externí zařízení (z pohledu procesoru, takže např. paměť či IO zařízení) prostřednictvím řadiče přerušení (nebo u jednodušších systémů přímo prostřednictvím procesoru). Ten zároveň rozhoduje, o jaké přerušení se jedná a rozhoduje, jaká ISR se má na jeho základě vykonat.

Z pohledu SW je ideální tvořit ISR co nejmenší, aby jejich vykonávání bylo co nejkratší. To především proto, že je během nich zakázáno další přerušení a my tak můžeme přijít o další informace. Proto je dobrou praxí si v ISR pouze uložit informaci o vyvolaném přerušení a zpracovat ji následně během kontroly již v klasickém výkonném kódu pomocí kontrolního cyklu. Toto je ovšem možné pouze v případě, jsme-li schopni zajistit vykonání reakce v přijatelném čase (např. pro stisk tlačítka na termostatu klidně stovky ms, ale pro nouzový spínač u soustruhu může být každá ms nepostradatelná).

Postup:

externí zařízení vyvolá přerušení
procesor dokončí aktuálně vykonávanou instrukci a uloží obsah program counteru na zásobník
procesor (nebo řadič přerušení) zjistí z tabulky vektorů přerušení adresu odpovídající ISR
procesor zakáže přerušení
procesor vykoná ISR
procesor povolí přerušení
po dokončení procesor načte uloženou adresu následující instrukce ze zásobníku a uloží ji do PC

SW interrupt

SW interrupty jsou vyvolány kódem, který na zařízení běží. Obvykle se k tomu užívá instrukce INT. SW interrupty jsou běžnější v zařízeních s operačním systémem, který na ně reaguje a zpracovává je svým standardním způsobem (typickým případem je zpracování výjimek (výjimky jsou SW přerušení)). V zařízeních bez OS si musíme ISR navrhovat sami, což je ovšem naprosto v pořádku. Stojí však za zvážení, zdali je to pro nás výhodné (např. platforma Arduino je má zakázané). Jsme-li schopni navrhnout SW tak, aby k situacím vyžadujícím SW přerušení nedocházelo, nemusíme je implementovat.

Rozdílem oproti HW přerušení je především synchronicita, protože SW přerušení je vyvoláno instrukcí, dochází k němu jen při tiku interních hodin, a tedy je synchronní.

Postup:

vyvolá se instrukce přerušení
uloží se stavové informace o právě zpracovávaném programu
zakáže se další přerušení
procesor zjistí, o jaké přerušení se jedná (podle operandu)
nalezne odpovídající ISR a vykoná ji
po návratu z podprogramu obnoví uložené stavové informace

Cyklické čtení periferií

Jedním z nejběžnějších způsobů práce s periferiemi je jejich cyklické čtení. Ve vestavěných systémech jsou velmi běžné periferie, které provádějí svou činnost nezávisle na řídícím mikrokontroléru (např. neustále snímají teplotu okolí), její výsledky ukládají do svých registrů a při dalším měření je přepíší bez ohledu na to, jestli je předtím mikrokontrolér četl. Jedná se o protiklad k přerušujícím periferiím, protože je zde čistě na mikrokontroléru, kdy data přečte.

Tento princip je nutné podpořit SW návrhem, tedy implementací cyklického čtení. Na jednodušších jednojádrových systémech je to naprosto běžný přístup - máme cyklus, který se vykonává neustále dokola, dokud je mikrokontrolér napájen (např. Arduino). Ten bývá často doplněn o úvodní možnost nastavení prostředků (část kódu, která se vykoná jen jednou - na začátku).

U vícejádrových systémů jsou možnosti širší. Můžeme mít např. jedno jádro, které pořád dokola pouze čte data z periferií a předává je ostatním ke zpracování.

Softwarové řešení připojení pomalých a rychlých periferii

Způsoby SW řešení připojení periferií opět dosti záleží na typu a vlastnostech kontroléru. Máme-li jednojádrový kontrolér, může pro nás být řízení pomalých periferií (jako např. LCD displeje) poměrně náročné.

Vezmeme-li si např. běžně používaný LCD 1602, máme dvě možnosti jeho řízení. Můžeme jej připojit přímo, což nám zabere minimálně šest GPIO pinů (plus další prostor na DPS pro napájení a zem), ale budeme s ním moci komunikovat relativně rychle. Nebo využijeme I²C převodník, který nám sníží počet pinů na dva (navíc společné pro všechna I²C zařízení), ale výrazně prodlouží komunikaci.


obr. 1: LCD 1602 (s I²C převodníkem)
zdroj: https://dratek.cz/arduino/1570-iic-i2c-display-lcd-1602-16x2-znaku-lcd-modul-modry.html

Rozhodnutí závisí na naší aplikaci. Pokud nám nevadí čekání, můžeme zvolit pomalejší metodu s tím, že zbytek systému bude během interakce s displejem čekat. Potřebujeme-li však co nejvíce minimalizovat prostoje, zvolíme metodu rychlejší (ovšem jen pokud máme dostatek IO pinů).

Podobné dilema nám vyvstává i u dalších pomalých periférií, jako jsou např. kamery. Zde navíc musíme brát v potaz i další prodlevu způsobenou následnou komunikací s externími systémy, kterým budeme velice pravděpodobně chtít získané snímky předat.

Tyto problémy značně redukují vícejádrové systémy, které umožňují vyhradit obsluze pomalých periferií konkrétní jádro a zbytek systému jimi není bržděn.

Rychlé periferie, jako např. joystick (což je interně jen sada tlačítek) často užívají přerušení a tedy na ně systém nemusí čekat. Obsluha přerušení však přináší vlastní problémy, které jsou popsané výše.

Zdroje

https://www.embedded.com/5-steps-to-designing-an-embedded-software-architecture-step-1/
https://www.embedded.com/5-steps-to-designing-an-embedded-software-architecture-step-2/
https://www.embedded.com/5-steps-to-designing-an-embedded-software-architecture-step-3/
Přispěvatelé Wikipedie, Přerušení [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 9. 01. 2023, 08:57 UTC, [citováno 22. 05. 2023] https://cs.wikipedia.org/w/index.php?title=P%C5%99eru%C5%A1en%C3%AD&oldid=22318942

Periferie

Principy řízení periferii, adresové mapování periferii, řadič přerušení, časovače, čítače, watchdog, řadič displeje, řadič klávesnice, programovatelné hradlové pole.

Úvod

Periferií můžeme rozumět jakékoliv zařízení, jež můžeme připojit k počítači, přičemž toto zařízení není klíčové pro chod počítače jako takového. Příklady: externí disk, tiskárna, klávesnice, monitor. Periferie rozdělujeme na

vstupní (I): získávají data z okolí
výstupní (O): poskytují data do okolí
vstupně/výstupní (I/O): dělají obojí z výše uvedeného

Jakým způsobem jsou ale periferie řízeny? Neboli, jakým způsobem daná periferie ví, kdy může pracovat?

K přenášení informací mezi procesorem a periferiemi slouží tzv. sběrnice. Ty slouží ale také ke komunikaci mezi částmi uvnitř mikroprocesoru nebo také mezi počítačem a okolím.

Rozlišujeme tři druhy sběrnic

adresová sběrnice
- pokud chce mikroprocesor data číst nebo je zapisovat, musí nějakým způsobem sdělit místo čtení i zápisu
- toto místo je identifikováno adresou, která je přenášena po adresové sběrnici
- zdrojem této informace je mikroprocesor
- počet bitů adresy odpovídá počtu vodičů adresové sběrnice
řídící sběrnice
- řídící sběrnice je souhrn jednotlivých signálů aktivních v různých časových okamžicích s různým významem, které mívají různé zdroje
- některé signály jsou generovány mikroprocesorem, některé mohou být ovlivňovány jinými bloky
- k jednotlivým blokům jsou pak přivedeny pouze signály jim patřící.
- mezi nejčastější signály řídící sběrnice patří například:
  - RESET
    - je jím vybaven každý mikroprocesor
    - aktivován je uživatelem nebo jiným přídavným obvodem
    - tento signál uvede mikroprocesor do jeho výchozího stavu
  - Memory Read (MR)
    - zabezpečuje časování čtení z pamětí či jiných bloků
  - Memory Write (MW)
    - zabezpečuje časování zápisu do pamětí či jiných bloků
  - Input/Output Read/Write (IOR/IOW)
    - slouží pro čtení z nebo zápis do zařízení
  - READY
    - určuje připravenost obvodu
datová sběrnice
- slouží pro přenos všech dat v počítači
- data jsou vždy přenášena mezi dvěma bloky počítače
- typickým příkladem tohoto přenosu je přenos z paměti do mikroprocesoru
- mikroprocesor se účastní, až na výjimku jako přijímač a vysílač všech přenosů v počítači
- v praxi je nutné, aby v jakémkoliv okamžiku byl aktivní pouze jeden vysílač, jinak řečeno budič sběrnice (pokud by tomu tak nebylo, hrozí zničení obvodu)
- je tedy nutné vybavit bloky připojované na datovou sběrnici obvody, které umožňují odpojení tohoto bloku od datové sběrnice (třístavové budiče sběrnice)
- nejdůležitější parametry datové sběrnice:
  - šířka neboli počet bitů (kolik bitů je schopno se přenést najednou; výrazně ovlivňuje čas přenosu; maximálně stejný počet bitů jako procesor)
  - časování

Sběrnice mohou být sdílené a nesdílené.

sdílená: sdílí vodiče pro adresy a data
- ISA sběrnice (už se léta nepoužívá)
nesdílená: zvlášť dráty pro data, adresy, řízení
- PCI sběrnice

Řadič

Jedná se o elektrický obvod, sloužící pro připojení periferií. Zároveň slouží jako mezistupeň pro komunikaci mezi periferiemi a zbytkem počítače. Tato komunikace probíhá skrze sběrnici.

Řadič displeje

Jedná se o mikrokontrolér, které se stará o výstup informací v podobě obrazu na monitor. Je zodpovědné za konverzi digitálního obrazu nebo video dat (kupříkladu z grafické karty) na formát, jež je zobrazitelný na obrazovce.

Řadič displeje take obstarává další funkce, jako je obnovovací frekvence monitoru, nastavení jasu, nebo elektrickou spotřebu displeje.

U dnešních stolních počítačů umožňuje připojení displeje skrze různá rozhraní (HDMI, Display Port, VGA...)

Řadič klávesnice

Řadič klávesnice je typicky mikrokontrolér zabudovaný v klávesnici samotné nebo v základové desce počítače. Skenuje klávesnicovou matici což je mřížka drátů a obvodů, které připojují každou klávesu k řadiči.

Pokud je některá z kláves stlačena, tak řadič tuto akci převede na digitální signál, který je zaslán skrze sběrnici procesoru. Na základě toho může operační systém, potažmo jiný software tuto akci vyhodnotit. Řadič také zajišťuje komunikační protokol mezi klávesnicí a počítačem, aby každý úhoz do klávesnice byl správně vyhodnocen.

Principy řízení periferií

Vstupní a výstupní zařízení bez ohledu na způsob připojení používají tři základní techniky řízení přenosu o které se stará řadič periferních zařízení:

programové řízení vstupu a výstupu
řízení na základě přerušení
přímý přístup k operační paměti (DMA – Direct Memory Access)

Programové řízení

Procesor řekne skrze sběrnici řadiči, že chce provést periferní operaci. Nastaví parametry a nakonec „start bit“. Řadič kontroluje start bit a pokud je tam log. 1, začne provádět operaci na zařízení. To, jakým způsobem bude operace provedena, záleží na řadiči. Po dokončení výsledek vystaví na výstup a procesor pomocí tzv. pollingu programově (v nějakém cyklu) kontroluje stav (zaměstnává tím procesor), dokud řadič nebude mít data ke zpracování.

Řízení na základě přerušení

Procesor řekne skrze sběrnici řadiči, že chce provést periferní operaci. Nastaví parametry a nakonec „start bit“. Řadič kontroluje start bit a pokud je tam log. 1, začne provádět operaci na zařízení. Po dokončení řadič informuje procesor, že má k dispozici data. Procesor má k dispozici řadič přerušení který umožňuje vyřizovat přicházející přerušení podle jejich nastavené priority.

Z hlediska procesoru jde o obsluhu přerušení, kdy si uloží svůj stav do paměti, obslouží událost jež přerušení vyvolala a poté pokračuje načtením uloženého stavu.

DMA

Řadič si požádá o přímý přístup do paměti, pokud mu bude vyhověno, tak výsledky operací prováděných řadičem jsou zapisovány do paměti bez účasti procesoru.

Jakým způsobem ale procesor ví, kde se daná periferie nachází? Tedy, jakou adresu má vystavit na adresní sběrnici?

Adresové mapování periferií

Operační systém si vytváří tzv. virtuální adresové prostory, které jsou abstrakcí nad fyzickou adresací paměti a dalších adresovatelných komponent počítače (hlouběji popsáno v otázce 2.1.7). Umístění periferních zařízení do některého z těchto prostorů nazýváme mapováním periferií.

Podle architektury počítače se vstupy/výstupy (periferie) dělí na:

paměťově mapované: registry jsou adresovány jako paměť, přístupné pomocí běžných operací čtení a zápisu do paměti
izolované: registry jsou přístupné pomocí speciálních instrukcí (zpravidla nazývaných IN a OUT); díky tomu jsou adresní prostory paměti a vstupů/výstupů oddělené

Těmto registrům, obsahující adresy I/O zařízeních, se také říká vstupní a výstupní řadiče

Paměťový prostor bývá obsazen více jak jednou fyzickou pamětí nebo periferním zařízením, a proto je nutné při přenosech dat s mikroprocesorem rozhodnout, které zařízení je ke komunikaci určeno. Tímto úkolem je právě pověřen adresový dekodér. Jeho výstupy jsou v podstatě signály CS (Chip Select) pro jednotlivé obvody.

Signál CS připojuje daný obvod k datové sběrnici tak, že jeho sběrnici přepne ze stavu vysoké impedance do aktivního stavu.


obr. 1: Připojení V/V zařízení v PC pomocí sběrnice

S rozvojem počítačů vznikla standardizace v oblasti připojování periferních zařízení došlo k rozdělení sběrnic na 2 úrovně:

vnitřní (obvodová) - sběrnice propojující funkční jednotky uvnitř integrovaného obvodu nebo tištěného spoje
vnější (systémová, společná) - sběrnice propojující zásuvné jednotky nebo funkční celky

Časovače

Jedná se o periferní I/O zařízení.

Časovač umožňuje plánovat události při kterých proces může vyvolat službu operačního systému. Zpravidla je k dispozici jen jeden časovač a programová časová fronta. Hardwarový časovač se pak používá pro odměření času do nejbližší události ve frontě.

Do fronty jsou události řazeny tím způsobem, že se zjistí, po které události má k nově přidávané události dojít a spočítá se a zaznamená čas (který má uplynout mezi těmito dvěma událostmi). Při vynulování časovače se vybere první událost z fronty, provede se příslušná akce a hardwarový časovač se přeprogramuje na čas následující události.

Čítače

Další z periferních I/O zařízení

Úkole čítače je inkrementovat obsah registru. Pokud se tato hodnota dostane na danou mez, čítač se vynuluje.

WatchDog Timer

Jedná se o speciální případ čítače, jež se často používá v embedded zařízeních. Jeho účelem je detekce selhání části zařízení.

Funguje na principu klasického čítače, který se po určité hodnotě na příkaz operačního systému vynuluje. Pokud k tomuto vynulování nedojde, tak WatchDog timer vygeneruje timeout signál. Pro procesor je tento signál znamením, že má zahájit opravující akce. Může jít například o vypnutí motorů, zahájení restartu apod.

Jeho využití je i v klasických operačních systémech, například pokud spouštíme nedůvěryhodný kód v režimu sandbox. WatchDog timer dává tomuto kódu pouze omezený čas procesoru, aby se zabránilo škodlivé činnosti tohoto kódu.

WatchDog Timer se také používá v operačních systémech reálného času aby bylo zajištěno, že proces dokončí svůj úkon v předem stanoveném čase. Pokud toto neudělá, bude terminován.

Tento čítač se často využívá tam, kde není možné k systému fyzicky přistoupit, nebo alespoň ne v rozumném čase. Systém se tedy musí být schopen zotavit sám.

Programovatelná hradlová pole (FPGA - Field Programable Gate Array)

Jedná se o digitální logické zařízení tvořené z logických hradel, které může být naprogramováno tak, aby jeho logické obvody plnily funkci definovanou uživatel i poté, co je zařízení vyrobeno. Takové hradlové pole může být uzpůsobeno přesně podle potřeb, aby splňovaly požadavky aplikace, jako zpracování signálu, zpracování dat, nebo řídící logika.

Jsou používány hlavně v řídících systémech, kde je díky tomu možnost splnit přesné požadavky aplikace. Mohou být také integrovány v dalším komponentách, jako jsou například senzory.

Příkladem použití FPGA může být například nutnost zpracovat výstup z mikrofonu. Můžeme toto předat procesoru a nechat ho, ať zjistí frekvence.

Nebo můžeme využít několik bloků programovatelných hradel, aby nám dokázali přečíst jednotlivé vzorky z mikrofonu. Tato logika je naprosto nezávislá na tom, co zrovna dělá procesor, čímž jsme ušetřili cenný čas procesoru. V praxi se FPGA používají tedy spíše jako doplněk již existujících logických celků.

Většina moderních FPGA však nejsou plně programovatelná a již obsahují bloky tvořené z napevno (hardwarově) naprogramovaných hradel.


obr. 2: Podoba moderního FPGA pro zpracování digitálního signálu

FPGA umožňují "doprogramování" řadičů. Například lze díky tomu nastavit řadiči klávesnice jiné typy klávesnic, jiné jazyky, nebo možnost vykonání akce při stisknutí více kláves zároveň.

Zdroje

Ing. Petr Olivka. Katedra informatiky FEI VŠB-TU Ostrava. Komunikace s perifériemi.[online]. @2010 [citováno 27. 04. 2023].
Dostupné z: https://poli.cs.vsb.cz/edu/arp/down/komunikace.pdf
Wikipedie: Otevřená encyklopedie. Řadič přerušení.[online]. @2023 [citováno 27. 04. 2023].
Dostupné z: https://cs.wikipedia.org/wiki/%C5%98adi%C4%8D_p%C5%99eru%C5%A1en%C3%AD
Wikipedia: Free encyclopedia. Video display controller.[online]. @2023 [citováno 27. 04. 2023].
Dostupné z: https://en.wikipedia.org/wiki/Video_display_controller
Kalábovi: Kalábovic wikina. Principy řízení a připojování periferních zařízení [online] @2022 [citováno 27.04.2023]
Dostupné z: https://kalabovi.org/pitel:isz:principy_rizeni_a_pripojovani_perifernich_zarizeni
Wikipedia: Free encyclopedia. Field-programmable gate array.[online]. @2023 [citováno 27. 04. 2023].
Dostupné z: https://en.wikipedia.org/wiki/Field-programmable_gate_array
Yossi Kreinin. How FPGAs work, and why you'll buy one [online] @2013 [citováno 27. 04. 2023].
Dostupné z: https://www.embeddedrelated.com/showarticle/195.php

Komunikační rozhraní

Sériové a paralelní, synchronní a asynchronní. Rozdělení podle rychlosti přenosu. Adresování a komunikace po rozhraní. Protokoly pro rozhraní. Rozhraní pro vývojové systémy JTAG, SPI, apod.

Komunikační rozhraní je část systému, která mu umožňuje vyměňovat si informace s jinými systémy. Je nutné, aby bylo rozhraní na obou stranách komunikace shodné (používalo stejný protokol).

Port vs sběrnice vs rozhraní

Tyto pojmy bývají často zaměňovány a pravdou je, že se jejich významy často překrývají. Nejsmysluplnější způsob, jak je rozlišit je patrně:

port
- fyzická část zařízení, která slouží k propojení s jiným zařízením (obvykle pomocí vodiče)
- jeho parametry jsou definovány standardem
sběrnice
- komunikační systém, který slouží k přenosu dat mezi zařízeními
- jeho zakončením je port
- vlastnosti sběrnic definují protokoly
rozhraní
- zastřešující pojem, který se používá pro označení obou předešlých samostatně i dohromady

Sériové a paralelní rozhraní

Význam:

sériový přenos znamená, že dochází k posílání bitů postupně, tedy jeden po druhém (obvykle po jednom vodiči)
paralelní přenos znamená, že dochází k současnému posílání více bitů (po více vodičích)

Z principu činnosti by se mohlo zdát, že paralelní rozhraní je jednoznačně lepší, jelikož v jeden moment dokáže poslat více dat, a tedy je rychlejší. Pravda je ovšem taková, že dnes se sériová rozhraní využívají mnohem častěji než ta paralelní. Důvody jsou následující:

při paralelním přenosu je nutné zajistit synchronizaci mezi jednotlivými vodiči, což je poměrně náročné (např. máme-li 8 bitovou paralelní sběrnici, potřebujeme, aby všech 8 bitů jednoho bytu dorazilo přibližně ve stejnou chvíli, aby se nám nepromíchal s následujícím)
kompenzační metody předešlého problému nejsou jednoduché a praktické (např. při paralelní komunikaci na DPS (desce plošných spojů) musíme v případě zatáček uměle prodlužovat kratší linky)
na delší vzdálenosti je také problém cena vícežilových kabelů
na DPS zabírají sériové linky méně místa - místo navíc přidává extra izolaci proti rušení
IC (integrované obvody) mají omezený počet vývodů, a tedy je pro ně sériové rozhraní lepší
u sériových linek je také mnohem jednodušší SW implementace rozhraní (pokud nemá mikrokontrolér odpovídající řadič)

Výhod paralelních rozhraní oproti dnešním sériovým rozhraním není mnoho. Tím nejdůležitějším je patrně obvodová složitost. Paralelní rozhraní mohou přenášet data "přirozeně" (z PC vyjde byte, který můžeme přenést tak jak je), kdežto u sériových rozhraní je nutné nejprve provést serializaci a následně deserializaci. K tomu se používají zařízení zvaná serializátor a deserializátor.

Využití

sériové rozhraní - prakticky v každém druhu komunikace
paralelní rozhraní - v rádiovém přenosu (s využitím např. PAM)

Příklady paralelních rozhraní, která byla nahrazena sériovými

paralelní port → USB (např. připojení tiskáren k PC)
PATA → SATA (připojení sekundární paměti PC)
PCI → PCI Express

Synchronní a asynchronní rozhraní

První význam (kterému se budeme věnovat níže):

synchronní rozhraní při komunikaci využívá tzv. hodinový signál, který synchronizuje činnost obou komunikujících zařízení
asynchronní rozhraní komunikuje bez pevně dané časové struktury (zprávy chodí nahodile), k identifikaci zpráv se často používají start-stop bity

Druhý význam (používá se spíše ve "vyšších vrstvách informatiky", např. programování):

synchronní rozhraní komunikuje tak, že odesílatel po odeslání zprávy čeká na její odpověď (tomuto přístupu se také říká blokující)
asynchronní rozhraní komunikuje bez nutnosti čekat na odpověď (po odeslání vykonává dále svou činnost = neblokující)

Synchronní rozhraní

Základem synchronních rozhraní je hodinový signál. Ten zajišťuje, že přijímající strana bude číst data jen ve chvíli, kdy je druhá strana odesílá a naopak (např. máme systém reagující na náběžnou hranu hodinového signálu. Když k ní dojde, odesílatel zapíše data (změní napěťovou hladinu linky) a současně je přijímač začne číst.). Hodinový signál může být:

sdílený
- obě strany pro něj mají společnou linku (přídavný vodič), např TWI (I2C)
- nedochází k rozsynchronizování
oddělený
- obě zařízení mají vlastní generátor hodinového signálu
- může dojít k rozsynchronizování (je nutné řešit - posílat synchronizační zprávy)

Asynchronní rozhraní

Asynchronní přenos (někdy též arytmický přenos) se od synchronního liší tém, že k synchronizaci dochází pouze během přenosu datového rámce. To znamená, že k začátku přenosu může dojít kdykoliv (k jeho identifikaci slouží tzv. start bit). Po přijetí start bitu se další bity čtou podle předem stanovené rychlosti (= baud rate; čímž v tuto dobu dochází k synchronizaci) a s přijetím tzv. stop bitu (ukončujícího datový rámec) komunikace končí, do přijetí dalšího start bitu.

Běžně používaná komunikační rozhraní

Zde budeme pojem rozhraním často zaměňovat s pojmem sběrnice.

JTAG

Rozhraní JTAG (Joint Test Action Group) se užívá pro verifikaci a testování HW vestavěných systémů (lze říci že PCB obecně). Jedná se o sériové rozhraní s nízkou režijí (overhead) přístupu. Připojuje se k Test Access Portu (TAP) na procesoru, prostřednictvím kterého lze přistupovat k registrům, které obsahují informace o stavu a činnosti procesoru.

Používá se k debugu SW vestavěných zařízení, testování různých úrovní HW zařízení, Boundary scanu (testování propojení bloků na PCB či uvnitř IC) a dalším testovacím účelům.

JTAG se používá ve většině vestavěných systémů, např.:

ARM procesory (používané např. v Raspberry Pi)
téměř všechna FPGA
některé 8 a 16 bitové mikrokontroléry s vyšším počtem vývodů

SPI

SPI (Serial Peripheral Interface) je, jak už název napovídá, sériové, asynchronní a full-duplexní rozhraní využívající společnou sběrnici. Jedná se o rozhraní typu single master, multi slave (jedno řídicí zařízení, více obyčejných). Používá se primárně pro připojení externí paměti, A/D převodníků, displejů, vzájemnou komunikaci mezi kontroléry, atd.

Fyzicky obsahuje (minimálně) čtyři vodiče:

SCLK
- slouží k distribuci hodinového signálu (od mastera k ostatním)
- k ní dochází jen během komunikace (= asynchronní rozhraní)
- je společný pro všechna zařízení
MOSI
- master out, slave in
- přenáší data od mastra k vybranému slavu
- je společný pro všechna zařízení
MISO
- master in, slave out
- přenáší data od vybraného slava k masteru
- je společný pro všechna zařízení
SS1...n
- slave select
- slouží k výběru konkrétního slave zařízení (toho, se kterým se bude právě komunikovat)
- každý slave má vlastní (SS1, SS2, ...)


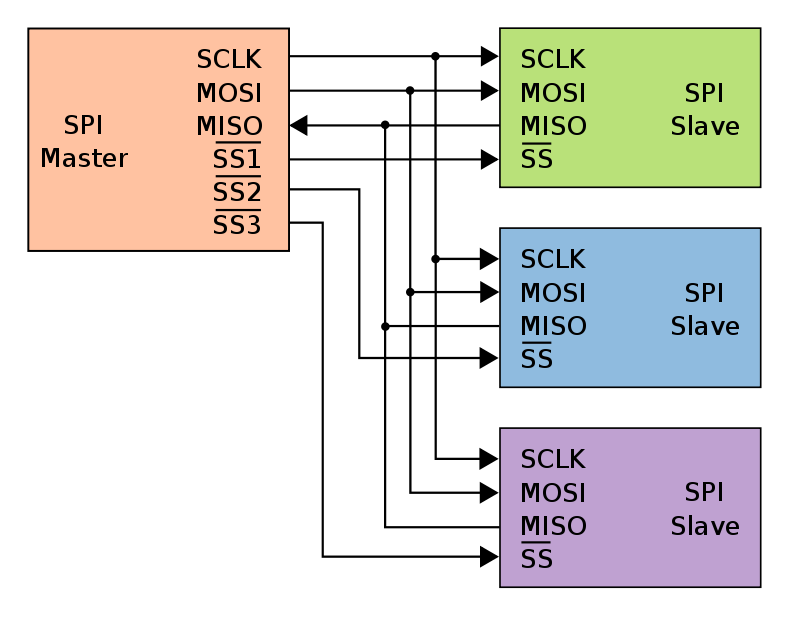obr. 1: Blokové schéma SPI zapojení
zdroj: en:User:Cburnett, CC BY-SA 3.0, via Wikimedia Commons

Adresování

Adresování probíhá přivedením log. 0 (piny jsou invertované) na vybraný SSn pin. Z toho vyplývá nevýhoda tohoto rozhraní - počet adresovacích pinů odpovídá počtu připojených zařízení.

Komunikace

master nastaví příslušný SSn pin na log. 0
začne generovat hodinový signál
začne posílat svá data na MOSI a zvolený slave zase na MISO (délka dat může být 8 nebo 16 bitů)
bod 3 se opakuje, dokud master nepřestane generovat hodinový signál a nenastaví příslušný SSn na 1

UART

UART (Universal Asynchronous Receiver-Transmitter) je standard popisující sériové asynchronní rozhraní pro komunikaci mezi dvěma zařízeními (existují i úpravy pro single master, multi slave komunikaci). Standard nedefinuje napěťové úrovně rozhraní, ty jsou určeny jinými komplementárními standardy, nejčastěji RS-232 a RS-485.

Existuje i varianta USART (Universal Synchronous Asynchronous Receiver-Transmitter), která umožňuje i synchronní činnost.

Fyzicky vyžaduje UART pouze dva vodiče (ale může jich být více, pro další pomocné úkoly, ty všask definuje konkrétní použitý standard):

Rx - přijímač; slouží k přijímání dat z druhého zařízení
Tx - vysílač; slouží k odesílání dat do druhého zařízení

Propojení je křížové, tedy RX - Tx.

Adresování

Adresace se zde neprovádí, jelikož je to komunikace 1 - 1.

Komunikace

UART umožňuje jak binární, tak znakovou komunikaci. Data jsou odesílána v paketech, které mají následující formát:

Start bit	Data	Paritní bit	Stop bity
1	5 - 9	0 - 1	1 - 2

K synchronizaci při komunikaci dochází jen při samotném posílání paketů a generování hodinových provádí obě strany samostatně. Levnější UART zařízení vzájemně synchronizují hodiny pouze při start bitu, ty pokročilejší při přijetí každého bitu zprávy.

Komunikace probíhá tak, že odesílatel postupně (v sérii) odešle všechny bity paketu. Příjemce je postupně ukládá do posuvného registru, po přijetí celého paketu dojde ke kontrole parity (k tomu je paritní bit) a pokud projde, překlopí se data do perzistentnějšího bufferu (aby šlo do posuvného registru přijímat další) a systému se oznámí, že jsou k dispozici data (interrupt nebo flag).

Obě komunikující zařízení musejí mít shodně nastavené následující parametry:

baud rate - určuje rychlost přenosu v bitech za sekundu (= frekvence hodinového signálu), nejnižší používaný je 75 Bd, poté se jedná o dvojnásobky, případně 1,5 násobky; nejběžnější jsou 9600 a 115200 Bd
přítomnost paritního bitu
počet datových bitů
počet datových bitů


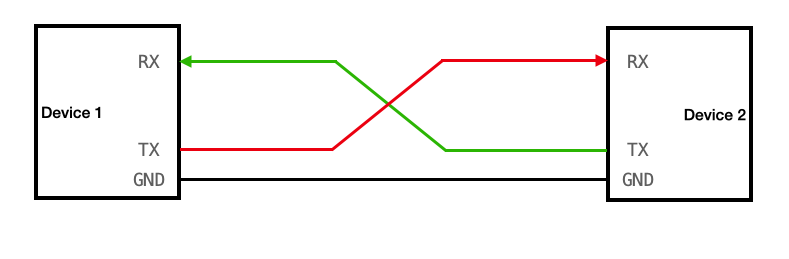obr. 2: Blokové schéma zapojení využívajícího UART
zdroj: https://vanhunteradams.com/Protocols/UART/UART.html

I²C

I²C (Inter-Integrated Circuit) je sériové, synchronní rozhraní typu multi master, multi slave (ale často se soužívá jako single master, multi slave). Používá se pro připojení periferií (paměti EEPROM, A/D D/A převodníky, displeje, senzory, atd.) k vestavěným systémům, ale i k PC. Původně bylo navrženo pro tzv. on-board komunikaci (mezi obvody na jedné DPS), ale úspěšně se používá i pro propojení oddělených zařízení (do 1 m je to s jistotou bezpečné).

I²C je ochrannou známkou společnosti Philips. Proto mnoho výrobců používá téměř identickou sběrnici TWI (Two Wire Interface).

Fyzicky vyžaduje I²C pouze dva vodiče - SDA (přenos dat), SCL (hodinový signál). Všechna zařízení se připojují na oba dva. Obě linky jsou zapojeny jako otevřený kolektor a musejí být pomocí tzv. pull-up rezistorů připojeny k log. 1 (aby byla zajištěna log. 1 v klidovém stavu).


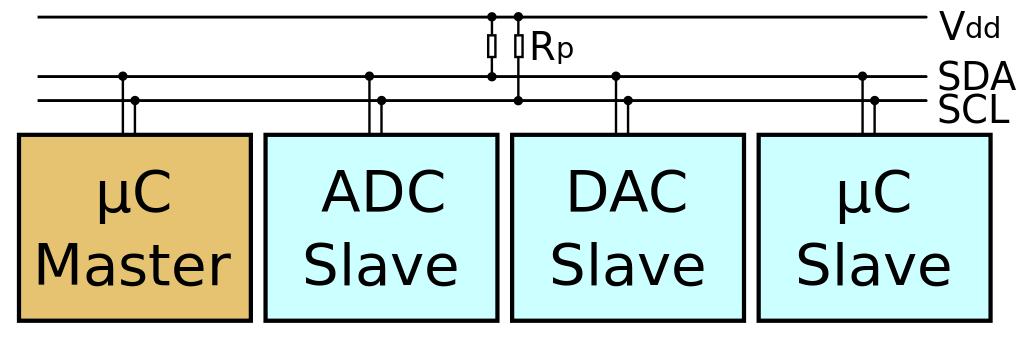obr. 3: Blokové schéma I²C zapojení
zdroj: en:user:Cburnett, CC BY-SA 3.0, via Wikimedia Commons

Adresace

Každé slave zařízení musí mít unikátní 7 nebo 10 bitovou adresu (ta je obvykle pevně daná). Ta je vysílána vždy na začátku každého požadavku (po příkazu START) a zařízení, kterému patří následně reaguje potvrzením.

Je tedy možné připojit najednou 128, resp. 1024 zařízení. Některá zařízení, u kterých je běžné, že je použto více kusů (např paměti), mívají část adresy nastavitelnou.

Komunikace

Postup:

master vyšle příkaz START
master vyšle adresu cílového zařízení (slave)
master vyšle R/W bit (určuje, jestli se má jednat o čtení, nebo zápis z/do slave)
slave vyšle ACK, jako potvrzení naslouchání
odesílají se data, podle směru R/W bitu (za každým bytem je další ACK)
master vyšle příkaz STOP

Komunikace je řízena metodou detekce kolizí. Jelikož může dojít k více požadavkům od více masterů najednou, musejí všechna zařízení při odesílání dat sledovat stav SDA. Objeví-li se tam rozdíl od odesílaných dat, znamená to kolizi. Kolize se vyřeší tak, že zařízení, které vysílá log. 0 a objeví na SDA log. 1 okamžitě ukončí přenos.

CAN

CAN (Controller Area Network) je sériové asynchronní rozhraní typu multi master, multi slave, využívaná nejčastěji pro vnitřní komunikační síť senzorů a funkčních jednotek v automobilu. Díky svým metodám pro vyhnutí se a řešení kolizí je CAN velmi vhodné pro systémy reálného času.

Adresace

CAN neadresuje jednotlivá zařízení, nýbrž přímo zprávy. Každá zpráva nese krom až 8 B dat také identifikátor, podle kterého příjemci rozhodují, jestli je zpráva zajímá, nebo nikoliv. Ten zároveň slouží k určení priority zprávy (nižší identifikátor, vyšší hodnota).

Komunikace

Jednotlivé stanice připojené na sběrnici vysílají svá data bez ohledu na to, je-li v sytému nějaký "zájemce" nebo nikoliv. Datové rámce proto neobsahují adresu příjemce, nýbrž jen identifikaci (11/29 b) která určuje, jaká data rámec obsahuje. Rámec je přijat všemi přijímači na sběrnici. Každý z přijímačů nezávisle použije identifikaci rámce k rozhodnutí, má-li být právě přijatý rámec akceptován, tj. předán k dalšímu zpracování nebo má-li být vymazán. Každý z přijímačů tak akceptuje pouze datové rámce, které jsou pro danou stanici významné.


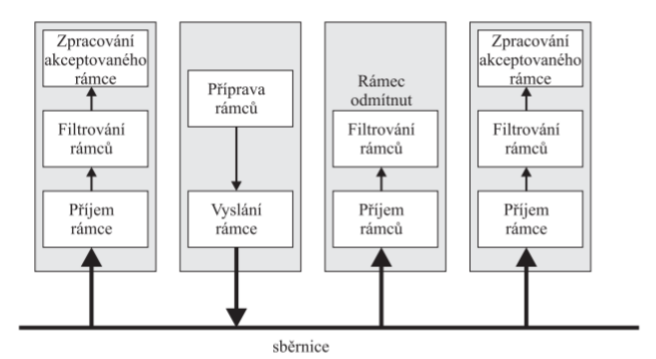obr. 4: Blokové schéma CAN
zdroj: ?

Rozdělení podle rychlosti přenosu

Rychlosti zde uvedené jsou jen velmi orientační a v reálných podmínkách se mohou lišit klidně i řádově.

Rozhraní	Teoretická maximální rychlost přenosu
SPI	25 Mbit/s
UART	250 kBd (při použití s běžnými RS-232 převodníky); = 250 kbit/s
I²C	3,4 Mbit/s (jednosměrně až 5 Mbit/s)
CAN	1 Mbit/s

Zdroje

DUDÁČEK, Karel. Sériová rozhraní SPI, Microwire, I2C a CAN. 2002. Dostupné také z: http://home.zcu.cz/~dudacek/NMS/Seriova_rozhrani.pdf
Přispěvatelé Wikipedie, Sériová komunikace [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 1. 01. 2023, 11:22 UTC, [citováno 12. 05. 2023] https://cs.wikipedia.org/w/index.php?title=S%C3%A9riov%C3%A1_komunikace&oldid=22285431
Přispěvatelé Wikipedie, Paralelní komunikace [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 13. 11. 2022, 18:21 UTC, [citováno 12. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Paraleln%C3%AD_komunikace&oldid=21879486
Wikipedia contributors, Comparison of synchronous and asynchronous signalling [online], Wikipedia, The Free Encyclopedia; 2023 Apr 5, 01:25 UTC [cited 2023 May 13]. Available from: https://en.wikipedia.org/w/index.php?title=Comparison_of_synchronous_and_asynchronous_signalling&oldid=1148256684
Přispěvatelé Wikipedie, Synchronní sériová komunikace [online], Wikipedie: Otevřená encyklopedie, c2021, Datum poslední revize 8. 08. 2021, 17:25 UTC, [citováno 12. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Synchronn%C3%AD_s%C3%A9riov%C3%A1_komunikace&oldid=20346129
Přispěvatelé Wikipedie, Arytmický sériový přenos [online], Wikipedie: Otevřená encyklopedie, c2021, Datum poslední revize 5. 08. 2021, 05:58 UTC, [citováno 12. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Arytmick%C3%BD_s%C3%A9riov%C3%BD_p%C5%99enos&oldid=20287670
Wikipedia contributors, JTAG [online], Wikipedia, The Free Encyclopedia; 2023 Apr 29, 17:45 UTC [cited 2023 May 12]. Available from: https://en.wikipedia.org/w/index.php?title=JTAG&oldid=1152346821
Přispěvatelé Wikipedie, Serial Peripheral Interface [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 19. 03. 2022, 22:57 UTC, [citováno 12. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Serial_Peripheral_Interface&oldid=21053330
https://community.silabs.com/s/article/what-is-the-maximum-spi-clock-speed-x?language=en_US
Wikipedia contributors, Universal asynchronous receiver-transmitter [online], Wikipedia, The Free Encyclopedia; 2023 May 13, 13:42 UTC [cited 2023 May 13]. Available from: https://en.wikipedia.org/w/index.php?title=Universal_asynchronous_receiver-transmitter&oldid=1154595277
Přispěvatelé Wikipedie, I²C [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 19. 03. 2022, 22:55 UTC, [citováno 13. 05. 2023] https://cs.wikipedia.org/w/index.php?title=I%C2%B2C&oldid=21053328
Přispěvatelé Wikipedie, CAN bus [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 20. 09. 2022, 13:42 UTC, [citováno 15. 05. 2023] https://cs.wikipedia.org/w/index.php?title=CAN_bus&oldid=21695185

Převodníky

Převodníky pro elektrické a neelektrické veličiny A/D, D/A . Architektura převodníků. Pojem přesnosti a kompenzace chyb. Definice kvantování a kvantovací šum. Vzorkování a vzorkovací frekvence - její dopad do přenášeného spektra (Aliasing).

Převodník je zařízení, jehož účelem je transformace mezi různými veličinami, případně mezi různými typy jedné veličiny.

Převodníky lze z pohledu veličin dělit na:

elektrické → elektrické - sem patří níže popsané A/D a D/A převodníky a pravděpodobně i modulátory (převádějí napětí na frekvenci, fázi, atd.)
neelektrické → elektrické - senzory (např. digitální teploměr, vlhkoměr)
elektrické → neelektrické - aktuátory (např. motory, LED)
neelektrické → neelektrické - např. kovářská výheň s měchem (převádí pohybovou sílu na teplo)

Vzorkování

Vzorkování je proces, při kterém dochází, vždy po uplynutí vzorkovací periody, k odebrání vzorku z analogového vstupního signálu. Odebraná hodnota (v tomto případě elektrické napětí) se poté obvykle dále zpracovává. Lze říci, že se jedná o proces diskretizace signálu v časové oblasti (definičním oboru).

Zařízení, které vzorkování provádí se nazývá vzorkovač (= vzorkovací obvod).

Důležité je při vzorkování zvolit správnou délku vzorkovací periody (respektive frekvenci vzorkovacího signálu1), aby nedocházelo k příliš velkému zkreslení a případným ztrátám informace. Podle Shannonova–Nyquistova–Kotělnikovova teorému (často se mu říká jen Shannonův–Kotělnikovův teorém) musí být vzorkovací frekvence nejméně dvakrát vyšší než nejvyšší frekvence obsažená ve vzorkovaném signálu. Řečeno matematicky:

\[ f_{vz} \geq 2 \cdot f_{max} \]

kde $ f_{vz} $ je vzorkovací frekvence a $ f_{max} $ maximální frekvence obsažená ve vzorkovaném signálu.

Aliasing

Je jev, při kterém dochází ke zkreslení výstupného signálu, a to pokud není splněna podmínka SNK teorému. Jako ochrana se používá antialiasing filtr (dolní propust zařazená před převodníkem). Ten nedovolí frekvencím vyšším, než je Nyquistova frekvence (minimální vzorkovací frekvence podle SNK teorému), vstoupit do převodníku.

Kvantování

Proces kvantování spočívá v přidělení každému vzorku (získanému vzorkováním) kvantizační hladinu. Počet hladin je určen počtem bitů, které máme k dispozici pro hodnoty výstupního signálu. Lidsky řečeno: spojitou škálu hodnot, kterých může vstupní signál nabývat rozdělíme na tolik dílů, kolik nám dává vztah $ N_{kv} = 2^{n_b} $, kde $ N_{kv} $ je počet dílů (hladin) a $ n_b $ počet bitů výstupního signálu a každému vzorku přiřadíme tu hladinu, která mu nejvíce odpovídá. Lze tedy říci, že se jedná o proces diskretizace signálu v oboru hodnot.

Nastavení hladin může být dvojího druhu:

lineární - každá hladina zabírá stejný interval (nejběžnější)
nelineární - intervaly jednotlivých hladin se liší (pro zvláštní účely; např. exponenciální, logaritmické)

Kvantizační šum

Je jev, který nastává, pokud je kvantování příliš hrubé (máme málo výstupních bitů). Jedná se o nepřesnost způsobenou tím, že se skutečná hodnota vzorku musí transformovat na nejbližší hladinu, která je ale tak vzdálená, že je tento rozdíl v následujícím použití digitalizovaného signálu patrný. Je to dobře vidět např. u fotografií, kde vznikají místo plynulých přechodů tzv. mapy (třeba u fotografií oblohy).

Lze ho řešit zvýšením počtu kvantizačních hladin (většinou příliš náročné) nebo přidáním dodatečného šumu (dither), který rozbije jednolitost oněch ostrých přechodů a výsledek poté působí plynule.

A/D převodník

A/D převodník slouží k převodu z analogového na digitální signál.

Poznámka: Druhy signálů

Analogový - spojitý v čase i hodnotě (= je definován funkcí se spojitým nebo částečně spojitým definičním oborem i oborem hodnot)
Diskrétní
- Vzorkovaný - není spojitý v čase, ale v hodnotě ano (= jedná se o posloupnost vzorků)
- Kvantovaný - je spojitý v čase, ale ne v hodnotě (= může nabývat pouze definovaných, které mají mezi sebou skokové rozdíly)
- Digitální - není spojitý ani v čase, ani v hodnotě (= kombinace vzorkovaného a kvantovaného)

Důvodem pro převod z analogového signálu na digitální je především možnost zpracování počítači - počítače umějí pracovat jen s diskrétními hodnotami a nemají nekonečnou paměť, proto potřebují konečný počet záznamů = vzorků (např. výstupy senzorů často bývají analogové, proto se ke kontroléru připojují přes A/D převodník; DSP (digitální signálové procesory) též zpracovávají digitalizovaný signál). Krom toho má digitální signál výhody při přenosu signálu - lze kontrolovat správnost signálu (např. kontrolní součty) a také nedochází ke ztrátám informací při kopírování signálu.

Princip převodu spočívá ve vzorkování signálu a následném kvantování těchto vzorků. Oba tyto procesy jsou popsány výše.

Druhy A/D převodníků

Přímé - výstupem je přímo počet kvant (tedy konkrétní hladina)
- Komparační - využívají odporové děliče spolu s komparátory
  - paralelní - nejrychlejší typ (celý převod probíhá v jednom okamžiku); princip popsán v sekci architektura A/D převodníků; vhodný max do 8 výstupních bitů (poté už příliš mnoho součástek)
  - s postupnou komparací - cílem je zjednodušení (= snížení počtu potřebných komponent) paralelních převodníků při zachování podobně krátké doby zpracování
- Kompenzační - využívají zpětnou vazbu; porovnávají vstupní napětí s výstupním a upravují ho, dokud nejsou rozdíly mezi nimi minimální; jsou konstrukčně jednoduché, relativně rychlé, středně drahé; používají se u PLC a mikrokontrolérů
  - čítací - hodnota čítače se zvyšuje, dokud nepřesáhne hodnotu vstupního napětí (zjišťujeme komparací přes zpětnou vazbu), poté je měření vzorku u konce
  - sledovací - stejný jako čítací, ale používá obousměrný čítač → může lépe reagovat na změny výstupního napětí
  - s postupnou aproximací - dochází k postupné úpravě jednotlivých bitů výstupu - vždy se vezme jeden bit (od MSB k LSB) a nastaví se na 1, pokud je výsledné napětí vyšší než vstupní, vrátí se na 0, jinak zůstává 1; když se dojde k LSB, vzorek je hotov
Nepřímé - dochází zde k mezi převodu na čas nebo frekvenci
- Integrační - využívá integrátor a tedy výstup je průměrná hodnota za určitou dobu
- S dvojitou integrací - často se používá v multimetrech; poměrně levný a obvodově jednoduchý
- Sigma-delta - umožňují dosáhnout velmi vysoké linearity převodu při vysokém rozlišení; jsou pomalé

Architektura A/D převodníků

Uvedeme zde pouze paralelní komparační převodník, jelikož je na pochopení asi nejjednodušší. Poté se jeho architekturu pokusíme zobecnit.


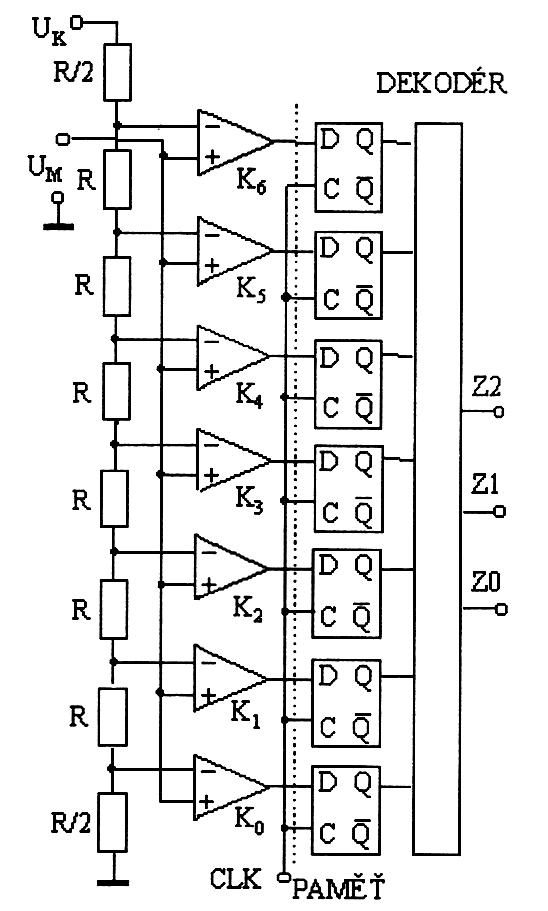obr. 1: Schéma paralelního komparačního převodníku
zdroj: HORÁČEK, Jaroslav. Prezentace pro předmět ELT na SOŠ SE Velešín

Základními částmi tohoto typu převodníku jsou:

odporový dělič
soustava komparátorů
soustava paměťových klopných obvodů a
dekodér

Jejich činnost a účel jsou popsány dále.

Odporový dělič

Je obecně soustava sériově zapojených rezistorů, kde za každým z nich následuje vývod, který při spojení se zemí vytvoří paralelní větev s napětím odpovídajícím úbytku na všech rezistorech před daným vývodem. V tomto případě mají všechny rezistory shodnou hodnotu $ R $ (až na první a poslední, ty mají $ \frac{R}{2} $), což znamená, že přírůstek napětí na vývodech je lineární.

Tento dělič je napájen referenčním napětím, které odpovídá maximálnímu vstupnímu napětí převodníku. Na výstupech děliče tedy bude rovnoměrně rozloženo toto napětí. Počet rezistorů děliče je roven počtu kvantizačních hladin převodníku.


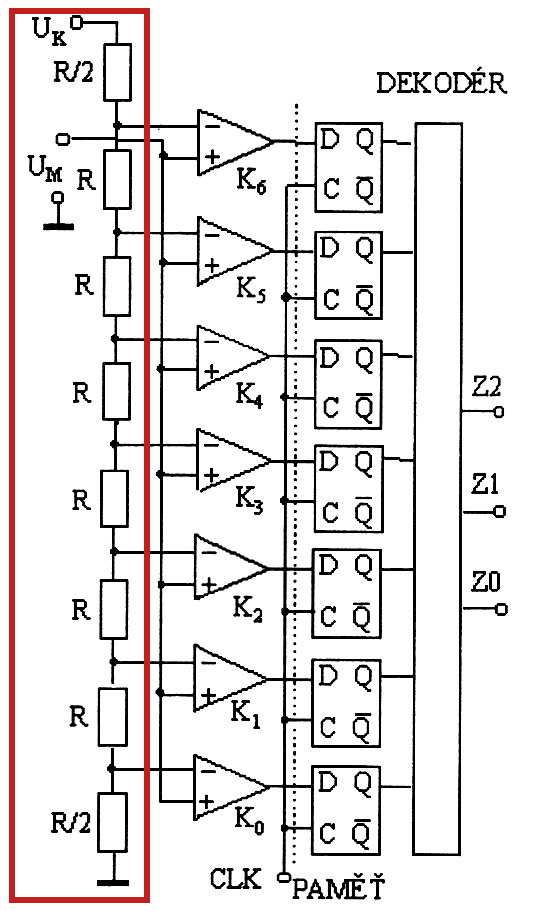obr. 2: Schéma paralelního komparačního převodníku (vyznačen odporový dělič)
zdroj: HORÁČEK, Jaroslav. Prezentace pro předmět ELT na SOŠ SE Velešín

Soustava komparátorů

Komparátor je obvod, který porovnává dva vstupní signály na základě velikosti jejich napětí a na výstup dává log. 1 či 0.

Zde máme pro každý vývod odporového děliče jeden komparátor (kromě vývodu za posledním rezistorem), který porovnává hodnotu napětí z vývodu děliče s aktuální hodnotou vstupního signálu.


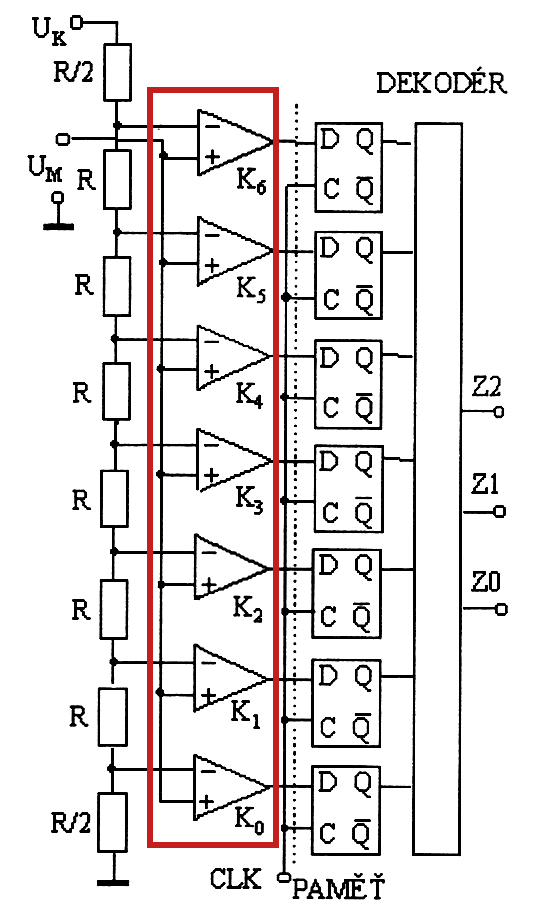obr. 3: Schéma paralelního komparačního převodníku (vyznačena soustava komparátorů)
zdroj: HORÁČEK, Jaroslav. Prezentace pro předmět ELT na SOŠ SE Velešín

Soustava paměťových klopných obvodů

Paměťový klopný obvod slouží k dočasnému uložení hodnoty napětí. Na jeden jeho vstup je přiveden vstupní signál, na druhý signál hodinový. Když dojde k hodinovému impulzu, do obvodu je uložena aktuální hodnota vstupního signálu a ta v něm setrvává do dalšího hodinového impulzu (poté je přepsána novou aktuální hodnotou). Uloženou hodnotu lze získat z výstupu obvodu.

Zde je za každým komparátorem jeden paměťový klopný obvod, který jako vstup přijímá hodnotu z daného komparátoru. Hodinový signál je pro celou soustavu společný.


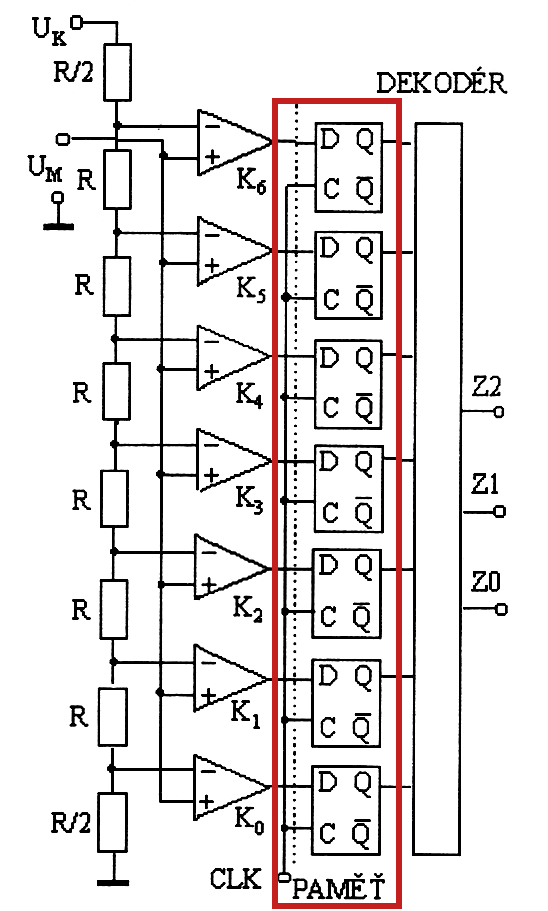obr. 4: Schéma paralelního komparačního převodníku (vyznačena soustava paměťových klopných obvodů)
zdroj: HORÁČEK, Jaroslav. Prezentace pro předmět ELT na SOŠ SE Velešín

Dekodér

Dekodér slouží k převodu z výčtu hodnot na odpovídající binární číslo, které je výstupem převodníku. Jako jeho vstupy jsou zde připojeny paměťové klopné obvody.


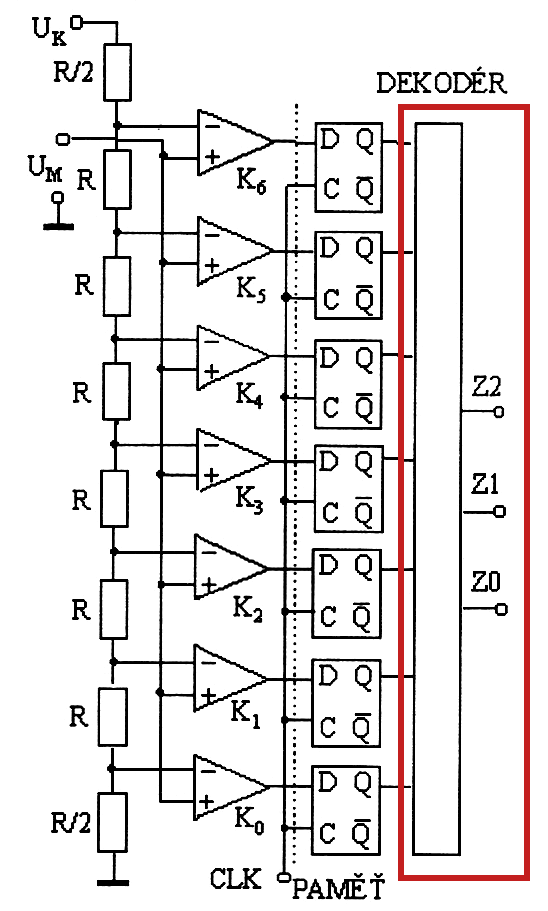obr. 5: Schéma paralelního komparačního převodníku (vyznačen dekodér)
zdroj: HORÁČEK, Jaroslav. Prezentace pro předmět ELT na SOŠ SE Velešín

Popis činnosti

Neustále dochází k dělení napětí na děliči a jeho komparaci se vstupním napětím. Výsledek komparace je však ignorován, dokud zdroj hodinového signálu nevyšle impulz. V reakci na něj dojde k uložení aktuálních výsledků komparace do paměťových klopných obvodů a jejich dekódování. Dekódovaná binární hodnota je na výstupu převodníku dostupná až do vyslání dalšího hodinového impulzu.

Vysvětlení kontextu

Jak bylo řečeno výše, proces A/D převodu spočívá ve vzorkování a kvantování vstupního signálu. Výše popsaná činnost tomu poměrně pěkně odpovídá - reakce na hodinový (vzorkovací) signál a následné uložení hodnoty (vzorku) do paměťových KO je proces vzorkování, kdežto komparace vstupního napětí s referenčními hodnotami (hladinami) je proces kvantování. Krom vzorkování a kvantování zde dochází ještě ke kódování (v dekodéru), to se však obvykle v popisu opomíjí.

D/A převodník

Jak název napovídá, D/A převodníky slouží k transformaci digitálního signálu na signál analogový. To je užitečné např. pro audiotechniku (ze zvukové karty do sluchátek), zobrazení signálu případně pro některé typy aktuátorů ovládaných mikrokontrolérem.

Druhy D/A převodníků

Nejběžnější jsou:

s váhovými odpory - vyžaduje velké množství přesných odporů s různými hodnotami
s odporovou sítí R-2R - poměrně jednoduché zapojení

Architektura D/A převodníků

S váhovými odpory


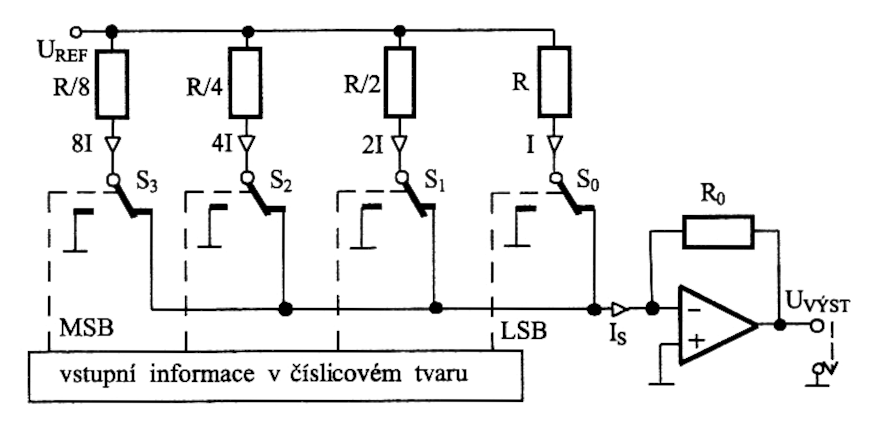obr. 6: Schéma převodníku s váhovými odpory (tranzistorové spínače jsou zde pro jednoduchost nahrazeny mechanickými)
zdroj: HORÁČEK, Jaroslav. Prezentace pro předmět ELT na SOŠ SE Velešín

A/D převodník s váhovými odpory se skládá ze dvou hlavních částí:

soustava odporů
soustava spínačů

Jejich činnost a účel jsou popsány dále.

Soustava odporů

Skládá se z $ n $ rezistorů (kde $ n $ je počet vstupních bitů převodníku), které tvoří paralelní soustavu. Ta je připojena k referenčnímu napětí. Poslední rezistor soustavy má hodnotu odporu $ R $ a každý předešlý poté polovinu toho následujícího (tedy $ \frac{R}{2} $, $ \frac{R}{4} $, atd.).


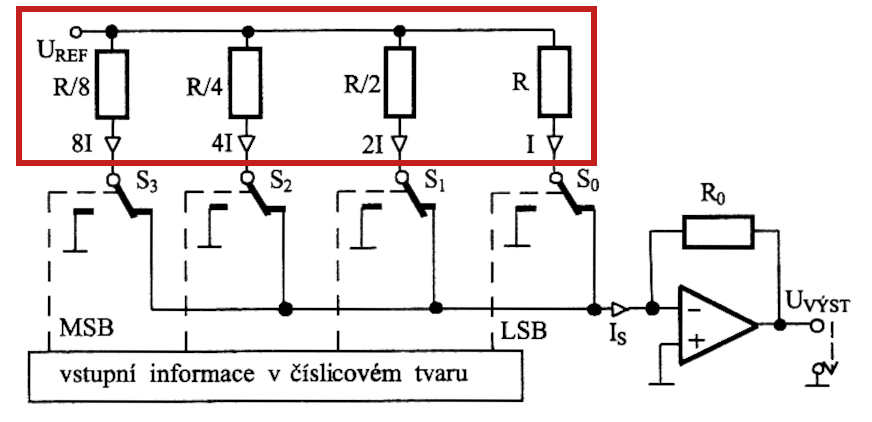obr. 7: Schéma převodníku s váhovými odpory (vyznačena soustava odporů)
zdroj: HORÁČEK, Jaroslav. Prezentace pro předmět ELT na SOŠ SE Velešín

Soustava spínačů

Ke každému odporu ze soustavy odporů je připojen jeden spínací prvek (nejčastěji MOS tranzistory), který odpovídá jednomu vstupnímu bitu (odporu s hodnotou $ R $ odpovídá LSB; odporu s nejnižší hodnotou MSB). Tedy je-li hodnota odpovídajícího bitu log. 1, tranzistor je otevřen, je-li 0, je uzavřen.


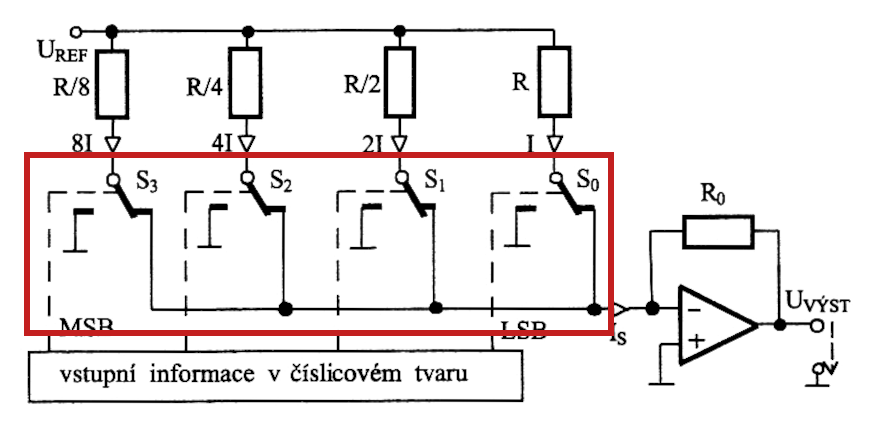obr. 8: Schéma převodníku s váhovými odpory (vyznačena soustava spínačů)
zdroj: HORÁČEK, Jaroslav. Prezentace pro předmět ELT na SOŠ SE Velešín

Princip činnosti

Přivedením vstupní binární hodnoty dojde k otevření příslušných tranzistorů a ty začnou propouštět proud z referenčního zdroje skrze příslušné rezistory do společného uzlu. V tomto uzlu dochází ke sloučení těchto proudů a na výstupu se objevuje napětí, které odpovídá výslednému proudu. Je nutno dodat, že koeficienty jednotlivých proudů odpovídají převráceným hodnotám koeficientů odporů, tedy $ I $ pro $ R $, $ 2I $ pro $ \frac{R}{2} $, atd.

S odporovou sítí R-2R

Architektura těchto převodníků je velmi podobná převodníkům s váhovými odpory. Hlavním rozdílem je, že vyžaduje pouze dvě hodnoty odporů ($ R $ a $ 2R $). Ty jsou zapojeny jako série děličů (s poměrem 2:1), vždy jeden dělič místo jednoho odporu u převodníků s váhovými odpory. Hodnoty protékajících proudů odpovídají proudům u převodníků s váhovými odpory.


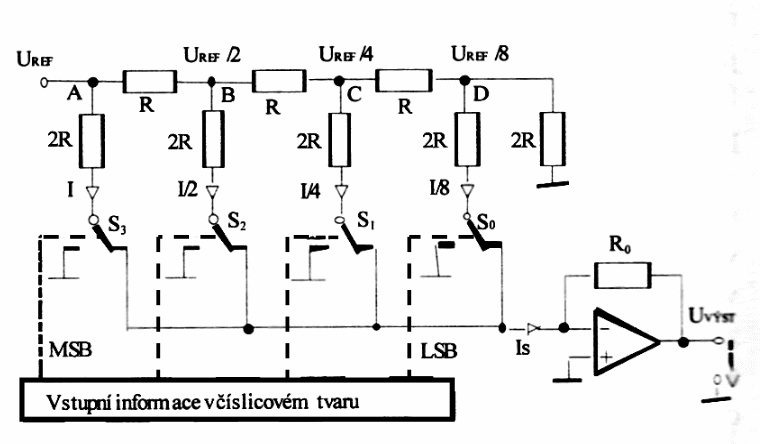obr. 9: Schéma převodníku s odporovou sítí R-2R (tranzistorové spínače jsou zde pro jednoduchost nahrazeny mechanickými)
zdroj: HORÁČEK, Jaroslav. Prezentace pro předmět ELT na SOŠ SE Velešín

Druhým rozdílem je, že spínací prvek je zde dvojice MOS tranzistorů buzených v protifázi (to bych však možná raději neuváděl - není jisté, že to tak je vždy).


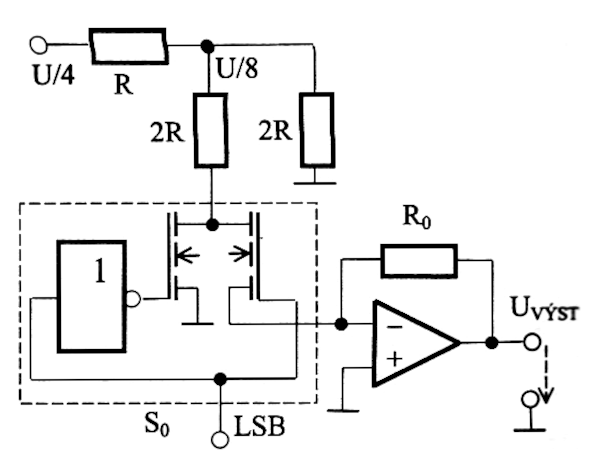obr. 10: Schéma jednoho bitu převodníku se skutečným spínačem
zdroj: HORÁČEK, Jaroslav. Prezentace pro předmět ELT na SOŠ SE Velešín

Přesnost převodníků

Přesnost je jedním ze základních parametrů převodníků. Můžeme na ni nahlížet ze dvou úhlů:

rozlišení - důležitým vlivem na přesnost převodníku je počet bitů; čím více bitů převodník má, tím více máme k dispozici kvantovacích hladin a tím detailnější výstup z převodníku získáme
kvalita součástek - dalším vlivem na přesnost je kvalita použitých součástek, protože i když budeme mít velmi vysoké rozlišení, potřebujeme zároveň aby nedocházelo k výběru špatných hladin (u A/D) a špatné interpretaci hladin (u D/A)

Kompenzace chyb

Jak již bylo uvedeno dříve, aliasing lze kompenzovat:

aliasing filtrem (dolní propust)

Kvantizační šum lze kompenzovat (rozvedeno zde):

zvýšením počtu kvantizačních hladin
přidání dodatečného šumu (dither)

Zdroje

Wikipedia contributors. Analog-to-digital converter [online], Wikipedia, The Free Encyclopedia, c2023, Datum poslední revize 28. 4. 2023, 14:11 UTC, [citováno 29. 04. 2023] https://en.wikipedia.org/w/index.php?title=Analog-to-digital_converter&oldid=1152147100
Přispěvatelé Wikipedie, A/D převodník [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 23. 01. 2023, 18:54 UTC, [citováno 29. 04. 2023] https://cs.wikipedia.org/w/index.php?title=A/D_p%C5%99evodn%C3%ADk&oldid=22375060
Přispěvatelé Wikipedie, Analogový signál [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 30. 01. 2023, 20:57 UTC, [citováno 29. 04. 2023] https://cs.wikipedia.org/w/index.php?title=Analogov%C3%BD_sign%C3%A1l&oldid=22395542
Přispěvatelé Wikipedie, Diskrétní signál [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 30. 01. 2023, 20:58 UTC, [citováno 29. 04. 2023] https://cs.wikipedia.org/w/index.php?title=Diskr%C3%A9tn%C3%AD_sign%C3%A1l&oldid=22395547
Přispěvatelé Wikipedie, Vzorkování [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 31. 01. 2023, 20:18 UTC, [citováno 29. 04. 2023] https://cs.wikipedia.org/w/index.php?title=Vzorkov%C3%A1n%C3%AD&oldid=22398751
Přispěvatelé Wikipedie, Kvantování (signál) [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 21. 05. 2022, 11:34 UTC, [citováno 29. 04. 2023] https://cs.wikipedia.org/w/index.php?title=Kvantov%C3%A1n%C3%AD_(sign%C3%A1l)&oldid=21301238
Kvantování signálu [online]. 2023-04-29 [cit. 2023-04-29]. Dostupné z: http://fyzika.jreichl.com/main.article/view/1357-kvantovani-signalu.
SCHWARZ, Daniel. Analýza a modelování dynamických biologických dat - Úvod do problematiky [online]. 2013-10-17 [cit. 2023-04-29]. Dostupné z: https://is.muni.cz/www/98951/41610771/43823411/43823458/Analyza_a_modelo/44257487/Bi0440-Schwarz-VJ01.pdf.
HORÁČEK, Jaroslav. Prezentace pro předmět ELT na SOŠ SE Velešín. [cit. 2023-04-29].

Porty

Paralelní porty, sériové porty (asynchronní, synchronní), porty komunikačních sběrnic (I2C, RS232, CAN-BUS, Ethernet apod.). Přímý přístup do paměti DMA. Použití HW přerušení komunikace.

Co je to port?

Port poskytuje rozhraní pro připojení periferního zařízení k počítačovému systému. Porty jsou standardizované např. tvarem či počtem vodičů podle toho, jaké zařízení umožňuje daný port připojit. Port je rozhraní mezi základovou deskou a periferním zařízením. Každý port je připojený na sběrnici, která tuto komunikaci zajišťuje. Struktura portu je dána jeho standardem.

Druhy portů

V počítačích se nejvíce používají dva druhy portů, které rozlišujeme podle toho, jaký typ sběrnice využívají:

sériové (tiskárny, modemy)
paralelní

Dříve se skrze tyto porty připojovala většina vnějších I/O periferií. Dnes se pro připojení většiny takových periferií používá USB port.

Způsoby komunikace

Podle toho, jestli mají jednotlivá zařízení clock rate dělíme komunikaci na dva způsoby

synchronní
asynchronní

Hlouběji je to popsáno v otázce 3.6.

Synchronní komunikace

Při synchronní komunikaci, běží obě dvě spojené strany na tzv. stejných hodinách. Vyžaduje jeden drát navíc, pomocí kterého jsou obě strany schopné se synchronizovat, takže jsou schopné zasílat / přijímat data stejnou rychlostí. Pokud by tomu tak nebylo, tak by jedna ze stran, s pomalejšími hodinami, například poslala řetězec 100100, ale ta druhá, s rychlejšími hodinami, řekněme 4x rychlejšími, by tento řetězec přečetla jako 11111111, protože poté co by dorazila první jednička v podobě vysokého napětí, tak než by se toto napětí stalo opět nízkým, rychlá strana už za tu dobu přečetla 4x vysoké.

Asynchronní komunikace

U asynchronního způsobu se nepoužívají společné hodiny. Namísto toho mají přednastavenou rychlost přenosu, tzv. baud rate. Je tedy zajištěné, že rychlost přenosu jedné strany, odpovídá rychlosti čtení druhé strany.

Sériové porty

Sériový port, také nazývaný COM port (označení z dob DOSu) je nejstarším druhem portu. To, jaké má piny, jejich rozložení a napěťové hodnoty (Jak velké napětí na pinu musí být, aby bylo interpretováno jako logická 1), je dáno standardem RS-232. Skládá ze z konektoru ve tvaru písmene D (D-sub) a obsahuje 9 pinů. Data se tímto portem přenášejí jako ucelený řetězec 1 a 0, reprezentovaný ve formě elektrických signálů. Sériový port poskytuje pouze jednu linku, po které se data přenášejí.

Sériové porty přenášejí jednotlivé byty za sebou. Při začátku komunikace zašle sériový port tzv. start bit, který má hodnotu 0. Po každém bytu, který odešle, zasílá stop bit, aby dal najevo, že byte je kompletní.

Jedná se o bi-direktionální komunikaci, tedy obousměrnou. Port dokáže data přijímat i odesílat. Díky tomu, že má rozdílné piny na přijímání (Rx) a odesílání (Tx), může port přijímat a odesílat data zároveň. Jedná se o full-duplex port.


obr. 1: Schéma zapojení dvou sériových portů,zde konkrétně základní sériový port D-SUB
Dostupné z: https://www.virtual-serial-port.org/article/what-is-serial-port/rs232-pinout/

Paralelní porty

Paralelní porty, na rozdíl od sériových můžou přenášet více bitů zároveň. Přenosová rychlost je tedy výrazně vyšší, nežli je tomu u sériové komunikace. Vyžadují tedy více datových linek po kterých se tyto data přenášejí. Konkrétně pro každý bit mají jednu linku, jsou tedy schopné přenést celý byte najednou.

Jsou schopné data jak přijímat, tak odesílat, jedná se tedy o bi-direktionální port ale pouze v jednom směru zároveň. Nemohou najednou data přijímat a odesílat. Jde tedy o half-duplex rozhraní.

Původní účel paralelního portu bylo k připojení tiskáren, ale časem se jeho použití rozšířilo na monitory a externí HDD disky.


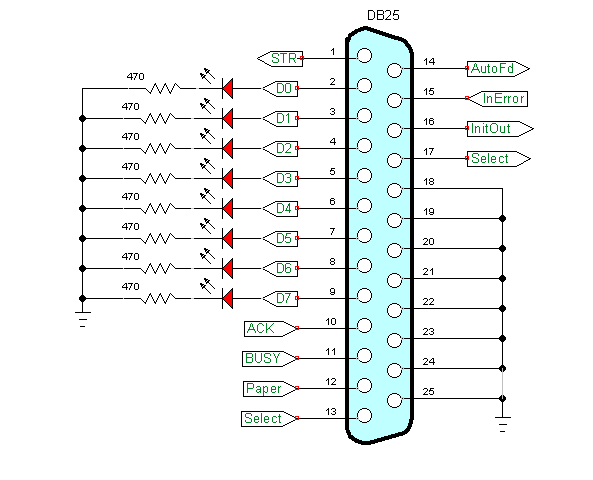obr. 2: Paralelní port (Každý datový kabel D0 - D7 má své uzemnění)
Dostupné z: https://www.bristolwatch.com/pport/pportbits.htm

Dnes se již paralelní porty nevyužívají. Důvodem je nutnost synchronizace všech datových linek. Toto byl velký problém například při ohnutí kabelu (U kabelů na "vnější" straně zatáčky trvá přenos o malý čas déle, což se ve výsledku nasčítá a bylo tedy nutné i řešit problémy fyzické vrstvy). Navíc s vývojem procesorů již bylo možné získat se sériovými porty dostatečně velkou přenosovou rychlost.

USB port

V dnešní době jsou oba zmíněné porty nahrazeny USB portem. Většina výrobců notebooků již sériové a paralelní porty (neplést si se sběrnicemi) na svá zařízení ani nepřidává.

K jedné USB sběrnici lze najednou mít připojeno až 127 zařízení. Každému připojenému zařízení je při připojení přiřazena adresa. Tomuto procesu se říká enumerace. Pokud připojíme 128 zařízení, nestane se nic, doslova. Tomuto zařízení nebude již adresa přiřazena a musíme nějaké zařízení odpojit, aby naše 128 zařízení fungovalo. Jeho struktura je dána standartem USB.

Na základě enumerace je poté každé adrese, tedy každému zařízení připojenému na USB sběrnici přiřazen mód, ve kterém bude fungovat, neboli, jakým způsobem bude odesílat data. Tyto módy jsou celkem 3:

interrupt
- používá se pro zařízení, které přenáší malé množství dat
- například myši, klávesnice
bulk
- používá se pro zařízení, které potřebují najednou velké množství dat, například tiskárny
- data se posílají např. v 64 bytových balíčcích
isochronous
- používá se pro streamovací zařízení, jako jsou například sluchátka
- data se zde posílají v reálném čase tak, jak zrovna zařízení potřebuje


obr. 3: USB port (USB A nahoře a USB B dole)
Dostupné z: https://www.electroschematics.com/usb-how-things-work/

USB využívá synchronní sériovou komunikaci.

Původní rychlost USB byla 12 Mb/s, ale s novými verzemi USB 2.0 a USB 3.0 tato rychlost vzrostla až na 5 Gb/s.

Porty komunikačních sběrnic

Na port můžeme pohlížet jako na vyvedení komunikační sběrnice. Ač se (původní) sériové a paralelní porty již téměř nepoužívají, tak sériové a paralelní sběrnice se využívají hojně. Příkladem může být USB port, který využívá USB sběrnici. USB sběrnice je druhem sériové sběrnice. USB port lze tedy označit za sérový port.

Struktura každého portu je dána protokolem pro přenos dat, který využívá.

I2C port

Jedná se o port, který je připojený k synchronní, multi-master/multi-slave sériovou komunikační sběrnici I2C . Termín slave označuje koncové zařízení, které je připojeno do portu, master je zařízení, ke kterému je koncové zařízení připojeno. U I2C platí, že komunikaci vždy zahajuje master, který mívá podobu mikrokontroléru.

Každý slave má svoji adresu, na základě které master určuje, s kterým zařízením si přeje komunikovat. Port obsahuje dva dráty, SDA, který slouží pro přenos dat a SCL, který slouží pro přenos hodinového signálu. Master generuje hodinový signál a slave používá tento vygenerovaný signál pro přijmutí dat, nebo pro odpověď masterovi.


obr. 4: I2C port s modulem pro sériovou komunikaci)
Dostupné z: https://www.ebay.co.uk/itm/203995295578

Pokud žádný slave nemá adresu, jež je masterem vystavena na sběrnici, tak žádný slave neodpoví.

Využití:

Základní specifikace definuje maximální hodinovou frekvenci na 100 kHz. Časem toto bylo navýšeno na 400 kHz. Sběrnice dokáže operovat v tzv. High speed módu, která umožňuje přenos rychlostí až 5 MHz.

I2C sběrnice se používá pro připojení I2C zařízení. Jmenovitě se jedná například o I2C sensory pomocí I2C portů.

Velké využití je v embedded systémech k připojení EEPROM paměti, A/D and D/A převodníků, I/O rozhraních a dalších. Důvodem je nutnost pouze 2 drátů, flexibilní rychlost a možnost adresovat jednotlivá zařízení připojená skrze I2C porty na I2C sběrnici.

RS-232

Jedná se o standart používaný pro sériovou komunikaci. V průmyslu se jedná o standart, především jeho modifikace:

RS-422
RS-485

Standard definuje asynchronní sériovou komunikaci pro přenos dat. Pořadí přenosu datových bitů je od nejméně významného bitu (LSb, často nesprávně LSB) po bit nejvýznamnější (MSb, často nesprávně MSB). Počet datových bitů je volitelný, obvykle se používá 8 bitů, lze se také setkat se 7 nebo 9 bity.

Využití:

Dnes se RS-232 standart využívá hlavně u CNC strojů nebo kontrolérů servo-motorů. Oproti USB je totiž jeho výroba mnohem levnější. Programování portů používajících standart RS-232 je také mnohem jednodušší.

Ethernet port

Jedná se o 8-pinový port který je na počítači připojený do řadiče internetového rozhraní. Port si nese označení RJ-45, nebo také LAN port. Struktura portu je daná stejnojmenným standardem Ethernet.

Jde o sériový port, který byl vyrobený čistě za účelem posílání paketů dat mezi jednotlivými zařízeními.

Kabel, který spojuje ethernetové porty dvou různých zařízení má v sobě celkem 8 drátů, jež tvoří 4 kroucené dvojlinky

Pokud propojujeme dvě stejná zařízení (není mezi nimi modem), tak je připojení drátů do portu na každém zařízení jiné, tedy Rx a Tx dráty jsou prohozené. Takovému zapojení se říká crossover. Nicméně Dnes již není nutné řešit, jaký druh zapojení používáme, zařízení si sama dokáží určit význam vodičů (= přehodit si je).


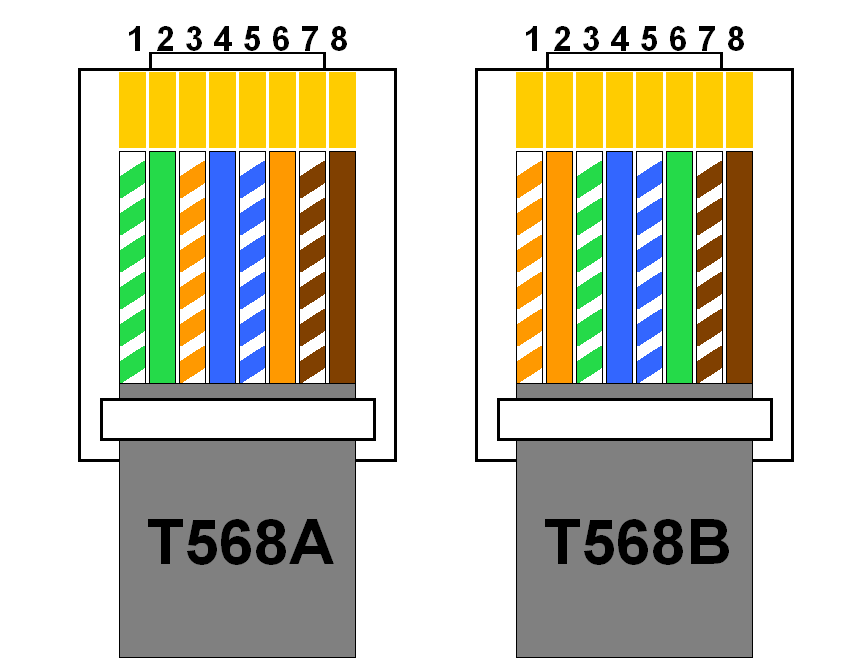obr. 5: Propojení dvou zařízení A a B skrze Ethernet Port
Dostupné z: https://napovedy.cz/post/268

Ethernetový port, v závislosti na jeho typu a použitém kabelu podporuje rychlosti:

10 Mb/s
100 Mb/s
1 Gb/s
10 Gb/s

Využití:

Využití Ethernet portu je hojné v oblasti sítí využívajících Ethernet protokol, konkrétně pro připojení zařízení k routeru, nebo propojení jednotlivých zařízení mezi s sebou.

CAN-Bus port

CAN (Controlled Area Network) je sama o sobě sběrnice. Na tuto sběrnici lze připojit port standartu RS-232 a používat ho jako CAN port, přičemž budeme využívat jen některé piny. CAN port je synchronní a sériový port.

O tom, jak funguje CAN sběrnice se lze dočíst v okruhu Komunikační rozhraní


obr. 6: RS-232 připojený na CAN sběrnici
Dostupné z: https://product-help.schneider-electric.com/Machine%20Expert/V1.2/en/tm5hwlmc/tm5hwlmc/LMC258-HW-Communication_Services/LMC258-HW-Communication_Services-3.htm

Využití:

Účelem bylo vytvořit sběrnici která umožní propojit různé zařízení, která mají různé porty. CAN port může tedy být jakýkoliv port, který umožní připojení ukázané na obrázku výše.

Hlavní použití je v automobilech pro propojení různých zařízení s centrální řídící jednotkou.

DMA (Přímý přístup do paměti)

Jedná se o způsob toho, jakým si zařízení připojené k portu žádá o přístup ke čtení/zápisu.

DMA je požádání o přímou práci s pamětí. Zařízení si poté do paměti přistupuje samo bez přičinění procesoru.

Jedná se o jeden z principů řízení periferií, o kterých si lze více přečíst v okruhu Periferie.

Hardwarové přerušení

Jedná se o další způsob, jakým si zařízení připojené do portu žádá a čtení, či zápis.

hardwarové přerušení spočívá v odeslání signálu procesoru pokaždé, když chce periferie číst či zapisovat data. Procesor přeruší to, co právě dělá, obslouží periferii a poté se opět vrátí ke své původní práci.

Jedná se o jeden z principů řízení periferií, o kterých si lze více přečíst v okruhu Periferie.

Zdroje

Javapoint. What is a Serial Port? [online], @2021. [citováno 28. 04. 2023]
Dostupné z: https://www.javatpoint.com/what-is-a-serial-port
Tutorialspoint. Kiran Kumar Panigrahi. Difference between Serial Ports and Parallel Ports [online], @2022. [citováno 28. 04. 2023]
Dostupné z: https://www.tutorialspoint.com/difference-between-serial-ports-and-parallel-ports
Wikipedia: Free Encyclopedia. *Synchronous serial communication [online], @2022. [citováno 28. 04. 2023]
Dostupné z: https://en.wikipedia.org/wiki/Synchronous_serial_communication
GeeksForGeeks. *Asynchronous serial data transfer [online], @2022. [citováno 28. 04. 2023]
Dostupné z: https://www.geeksforgeeks.org/asynchronous-serial-data-transfer/
ComputerHope. *Serial Communication Methods – Synchronous & Asynchronous [online], @2022. [citováno 28. 04. 2023]
Dostupné z: https://pijaeducation.com/communication/serial-communication-methods-synchronous-asynchronous/
Pija Education. *Parallel port [online], @2020. [citováno 28. 04. 2023]
Dostupné z: https://www.computerhope.com/jargon/p/paraport.htm
P. Marian. *USB Pinout, Wiring and How It Works [online], @2014. [citováno 28. 04. 2023]
Dostupné z: https://www.electroschematics.com/usb-how-things-work/
Bhimappa M. *I2C Protocol and Multi-master concept in I2C[online], @2020. [citováno 28. 04. 2023]
Dostupné z: https://www.linkedin.com/pulse/i2c-protocol-multi-master-concept-bhimappa-mali
Wikipedia: Free Encyclopedia. *RS-232 [online], @2022. [citováno 28. 04. 2023]
Dostupné z: https://en.wikipedia.org/wiki/RS-232
Sandeep Bhandari . *Difference between RJ45 and RS232 [online], @2023. [citováno 28. 04. 2023]
Dostupné z: https://askanydifference.com/cs/difference-between-rj45-and-rs232/
Grant Maloy Smith. *What Is CAN Bus (Controller Area Network) and How It Compares to Other Vehicle Bus Networks [online], @2021. [citováno 28. 04. 2023]
Dostupné z: https://dewesoft.com/blog/what-is-can-bus

Architektura softwaru řízení sítí periferii

Robotický operační systém (ROS). Řízení periferii v reálném čase. Sledování extrémně rychlých a pomalých veličin (v čase).

Robotický operační systém je vysvětlen v otázce č. 3.3 Architektura operačních systémů užívaných ve vestavných systémech.

Co to je řízení v reálném čase a proč jej potřebujeme?

De facto jde o adaptaci systému na reálnou situaci bez odezvy, nebo s velmi, velmi, velmi, velmi atd. malou odezvou.

Příkladem budiž sešlápnutí plynového nebo brzdového pedálu v autě. Po sešlápnutí pedálu se auto okamžitě rozjede nebo naopak brzdí. Mezi stiskem pedálu a akcelerací/decelerací není téměř žádná odezva. Postup je takový:

Shromáždíme data (senzorikou)
Data zpracujeme
Aktualizujeme výstup v definovaném časovém rámci (nesmí být překročen)

Pokud bychom nedodrželi časový rámec, auto by nezrychlilo, nebo naopak nebrzdilo.

Princip řídícího systému

senzorika (shromažďujeme data)
řídící jednotka (MCU) - vyhodnotí a zpracuje data
adaptace systému (chod motoru, otevření/zavření ventilu apod.)
komunikace mezi jednotlivými prvky systému

Komunikace by měla být nedílnou součástí celého procesu.


obr. 1: Funkční prvky řízení real-time
zdroj: Texas Instruments: What is “real-time control” and why do you need it? [online]. 2022 [cit. 2023-05-12]. Dostupné z: https://e2e.ti.com/blogs_/b/analogwire/posts/what-is-real-time-control-and-why-do-you-need-it

Senzorika

Senzory zajišťují sběr (měření) dat (napětí, proud, atmosférická vlhkost či teplota, rychlost motoru...). V ideálním případě je potřeba je naměřit s nejvyšší precizností, tak aby potenciální výstup odpovídal aktuální situaci.

CPU

Vstupní data je třeba zpracovat v co nejmenším časovém intervalu, tak, aby mohli následně na základě příkazů, reagovat další periferie (motor, píst, ventil...), optimálně v řádu jednotek mikrosekund.

Adaptace

MCU zpracuje získaná data a na základě jejich vyhodnocení pošle souvztažný příkaz do periférií. Např. změna pracovního cyklu (duty-cycle) PID regulátoru, je adaptací systému.

Komunikace

Přesná a rychlá komunikace mezi komponenty prostřednictvím Fast Serial Interface nebo Ethernet.

Real-time řízení v robotice

potřebujeme neustále měnit pozici motoru (třeba serva) robotické ruky a to s přesností na desítky mikrometru
docílíme toho tím, že budeme neustále sledovat pozici motoru a příkon, resp. aktuální proud a napětí
MCU následně vyhodnotí aktuální data s požadovanými a dle toho upraví střídu PWM signálu (motor se otočí o požadovaný úhel)
toto se celé musí odehrát v řádu mikrosekund


obr. 2: Schéma řízení motoru real-time
zdroj: Texas Instruments: What is “real-time control” and why do you need it? [online]. 2022 [cit. 2023-05-12]. Dostupné z: https://e2e.ti.com/blogs_/b/analogwire/posts/what-is-real-time-control-and-why-do-you-need-it

Níže je znázorněno schéma řízení DC motoru v reálném čase. Zpětnou vazbu zde poskytují rezistory, které vrací údaje o těchto dvou veličinách do MCU. MCU následně upraví PWM signál a otočí motorem.


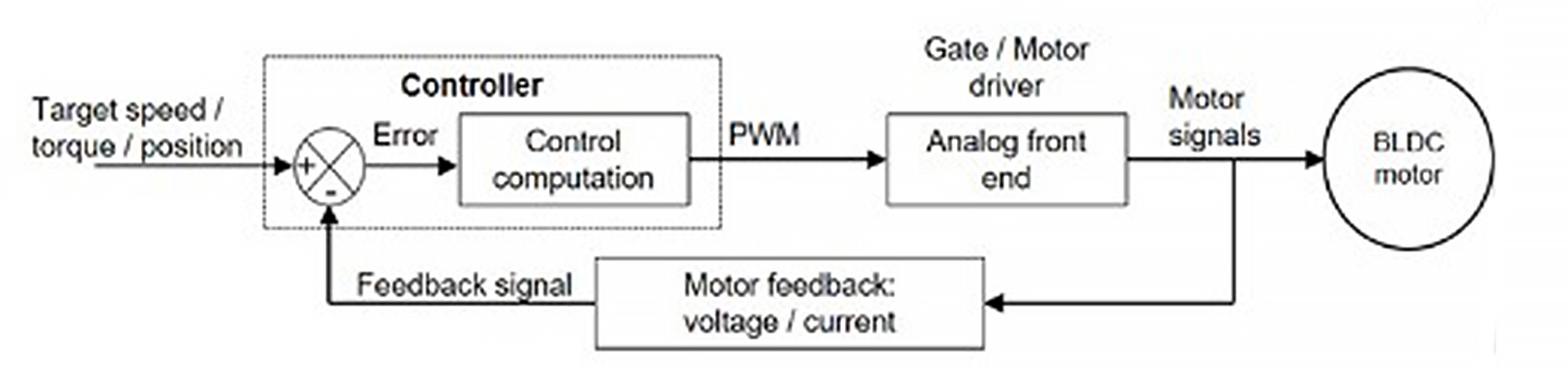obr. 3: Schéma řízení DC motoru real-time a zpětné vazby
zdroj: How to achieve efficient, reliable and accurate actuation in real-time motor control systems [online]. 2022 [cit. 2023-05-12]. Dostupné z: https://e2e.ti.com/blogs_/b/analogwire/posts/how-to-achieve-efficient-reliable-and-accurate-actuation-in-real-time-motor-control-systems

PID regulátor

Co to je?

Představte si, že jste regulátor a potřebujete korigovat množství vody ve vaně. která je aktuálně prázdná. Pustíte vodu, naplno. Vana se plní. Kohoutek trochu přivřete, protože se bojíte, že voda přeteče. Nicméně, nedali jste do vody špunt, tedy voda začne klesat. Vy na to zareagujete opětovným otevřením kohoutu (špunt tam dát neumíte, protože jste regulátor :-D). Tak voda začne opět stoupat, jenže když je voda až na okraji vany, tak kohoutek téměř zavřeme, ale voda stále teče.

Odtokovým kanálem voda teče pryč a kohout dodává menší množství vody, hladina klesá. Otočíme kohoutem více a dostáváme se do stavu, kdy objem odtékající vody je roven vodě přitékající, hladina se nemění a špunt nepotřebujeme.

JSME DOBRÝ REGULÁTOR!

Reálný příklad PID regulátoru je u mikropáječky a regulace teploty. Regulátor bude měřit teplotu a na základě ní ovlivňovat tok proudu, aby páječku nepřepálil. PID regulátor musí vědět, jaká bude požadovaná teplota, na kterou má páječku roztopit.

Složky PID regulátoru

Složka P - proporcionální, jedná se o zesilovač. Regulátor odečte změřenou teplotu od požadované a rozdíl (odchylku) vynásobí konstantou. Výsledkem je výkon, kterým bude páječka topit. Bude-li teplota o mnoho nižší, tak se výkon o mnoho zvýší. Čím více se bude změřená teplota blížit teplotě požadované, tím se výkon bude zvyšovat o menší hodnotu. Nastavíme-li konstantu na hodnotu jedna a bude-li teplota o 10 stupňů nižší, tak se výkon zvýší o 10 procent. Nastavíme-li konstantu na 100 a teplota bude nižší jen o stupeň, tak se výkon o 100 % zvýší. Problémem samotného P regulátoru je, že odchylka může poměrně hodně kmitat (moc výkonu / málo výkonu) a neustálý se na nule (dosažení výkonu dle požadované teploty).

\[u(t) = r_0e(t)\]

$u(t)$ - akční zásah
$r_0$ - konstanta (činitel zesílení)
$e(t)$ - regulační odchylka (rozdíl teplot)

Pásmo proporcionality udává, v jakém rozsahu je regulátor schopen regulovat, aniž by dosáhl svého limitu.

\[pp = \frac {1}{r_0} * 100\]


obr. 4: Chování P složky PID regulátoru
zdroj: Regulace od Jardy: Vše co potřebujete vědět k zaregulování PID [online]. 2006 [cit. 2023-05-12]. Dostupné z: https://ucebnaaut.wz.cz/wp-content/uploads/2017/11/Plynul%C3%A1-regulace-PID.pdf

Složka I - Integrační složka, integrační regulátor vezme regulační odchylku, vynásobí ji konstantou a přičte ke své složce. Bude-li změřená teplota vyšší, než požadovaná, bude se integrační složka snižovat, pokud bude teplota nižší než požadovaná, bude se integrační složka zvyšovat. Pokud bychom měli samotný integrační regulátor, bude topit nejdříve málo, výkon se zvýší a po dosažení požadované teploty se výkon bude opět snižovat. Bude-li konstanta příliš velká, zvýší se neoptimálně výkon a teplota příliš překročí teplotu požadovanou. Přibližování ideální teplotě je zde plynulejší a odchylka tolik nekmitá kolem 0 (požadované teploty), jako u P regulátoru.

\[u(t) = r_i \int{e(\tau)d(\tau)}\]

$r_i$ - zesílení integračního regulátoru

PI regulátor - vzorec

\[u(t) = r_0e(t) + r_i\int{e(\tau)d(\tau)}\]

Složka D - vezme rychlost změny odchylky a vynásobí ji konstantou. Opět, klesá-li teplota, derivační složka zvyšuje výkon. Čím rychleji klesá teplota, tím větším výkonem se ji regulátor snaží navýšit. Obráceně, pokud teplota klesne, derivační složka okamžitě zareaguje. Tedy začneme-li pájet, tak derivační odchylka okamžitě zvýší výkon páječky. Velikost konstanty se projevuje prudce na výkonu. Velká konstanta způsobí, že se na požadovanou teplotu bude páječka dostávat pomalu, ale bude zato prudce reagovat na změnu. Nízká konstanta naopak působí tak, že regulátor bude na změny reagovat mnohem pomaleji. Je to podobné jako brzdění v autě. Pokud před námi auto brzdí, tak také brzdíme, současně vyhodnocujeme rychlost s jakou se automobily k sobě přibližují (derivace vzdálenosti v čase). Pokud je rychlost velká, tak víte, že dotyčný před vámi musel sešlápnout brzdu pořádně. Tedy uděláte totéž, ačkoli jste ještě dost daleko. Derivační složka tedy v předstihu de facto zesiluje proporcionální složku. Potlačíme kmitání kolem 0.

\[u(t) = r_d \frac{de(t)}{dt}\]

PID regulátor - vzorec

\[u(t) = r_0e(t) + r_i\int{e(\tau)d(\tau)} + r_d \frac{de(t)}{dt}\]


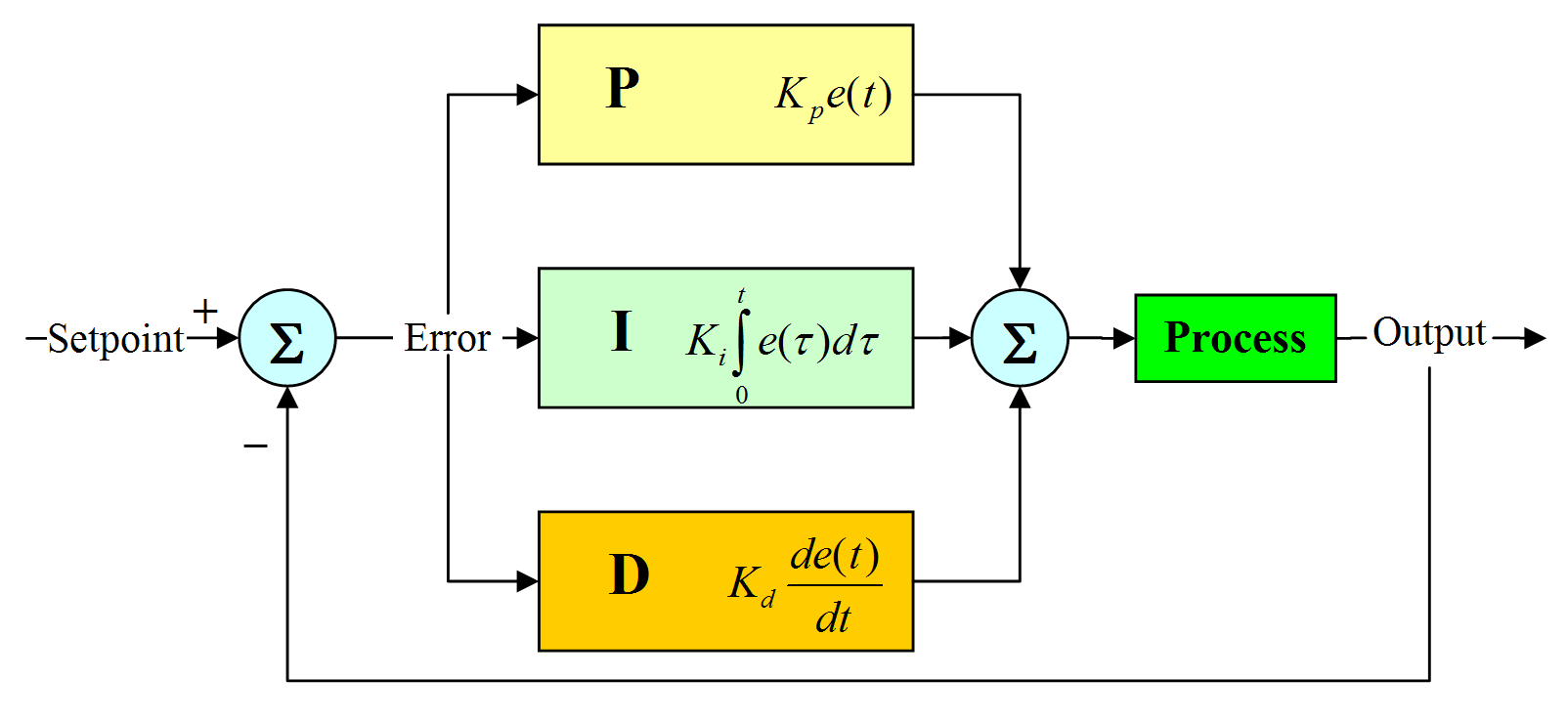obr. 5: Schéma PID regulátoru
zdroj: PID Scheme. In: Wikipedie: Otevřená Encyklopedie [online]. 2007 [cit. 2023-05-13]. Dostupné z: https://commons.wikimedia.org/wiki/File:Pid-feedback-nct-int-correct.png

ZDROJE

Texas Instruments: What is “real-time control” and why do you need it? [online]. 2022 [cit. 2023-05-12]. Dostupné z: https://e2e.ti.com/blogs_/b/analogwire/posts/what-is-real-time-control-and-why-do-you-need-it
How to achieve efficient, reliable and accurate actuation in real-time motor control systems [online]. 2022 [cit. 2023-05-12]. Dostupné z: https://e2e.ti.com/blogs_/b/analogwire/posts/how-to-achieve-efficient-reliable-and-accurate-actuation-in-real-time-motor-control-systems
Regulace od Jardy: Vše co potřebujete vědět k zaregulování PID [online]. 2006 [cit. 2023-05-12]. Dostupné z: https://ucebnaaut.wz.cz/wp-content/uploads/2017/11/Plynul%C3%A1-regulace-PID.pdf
Bastlírna HWKitchen: Rychlé seznámení s PID regulátorem [online]. 2019 [cit. 2023-05-13]. Dostupné z: https://bastlirna.hwkitchen.cz/rychle-seznameni-s-pid-regulatorem/

Pulzní modulace

Modulace obecně

Nejprve je třeba vysvětlit, co to vlastně je modulace. Poměrně dobrá definice z Wikipedie zní:

...proces, kterým se mění charakter vhodného nosného signálu pomocí modulujícího signálu.

Trochu hlouběji: máme signál (např. reprezentující data), který chceme nějakým způsobem použít (nejčastěji přenést), ale jeho aktuální forma není pro dané použití vhodná. Potřebujeme jej tedy upravit tak, aby výsledek odpovídal požadovanému užití. Tato úprava se nazývá modulace. Provádí se pomocí modulátoru, do kterého je přiveden náš signál (tzv. modulační signál) a zároveň nosný signál. Činností modulátoru je úprava nosného signálu podle zvoleného typu modulace (viz níže) a aktuální hodnoty modulačního signálu - např. používáme-li PWM (pulzně šířkovou modulaci) a hodnota modulačního signálu se zvyšuje, dochází ke zvyšování střídy signálu nosného.

Typy modulace lze dělit různě. Za základní dělení lze považovat dělení podle typu nosného signálu:

spojitá modulace – nosný signál má harmonický průběh (lze jej popsat funkcí sinus či kosinus)
- analogová - modulační signál je analogový (má spojitý průběh); např. pro rádio AM (amplitudová modulace) a FM (frekvenční modulace)
- digitální – modulačním signálem je diskrétní (≈digitální; jeho průběh není spojitý); např. ASK (Amplitude-Shift Keying), FSK (Frequency-Shift Keying)
diskrétní (pulzní) modulace – nosný signál má nespojitý průběh (někdy se také nazývá taktovací signál); této skupiny se týká otázka
- nekvantovaná - modulační signál je analogový; např. PWM (pulzně šířková modulace)
- kvantovaná - modulační signál je diskrétní; např. PCM (pulzně kódová modulace)

Důležité pojmy

modulační signál – vstupní signál; modulujeme jím nosný signál
nosný signál – signál s parametry vhodnými pro naše použití; modulujeme jej modulačním signálem
modulovaný signál – výsledný signál = výstup procesu modulace
modulátor - zařízení, které provádí modulaci
modulační produkty – složky modulovaného signálu (tento pojem se používá hlavně při zpětném rozkladu modulovaného signálu, např. při frekvenční analýze)
jednoduchá modulace – modulace zpracovávající jeden modulační signál
složená modulace – modulace zpracovávající několik modulačních signálů najednou

Pulzní modulace

Jak již bylo řečeno výše, u pulzních modulací je nosný signál nespojitý, přesněji řečeno, jedná se o periodickou posloupnost obdélníkových impulzů. Nejběžnější použití pulzní modulace je u A/D převodníků a pro zdrojové kódování.

Nekvantované

Nekvantované modulace se dále dělí podle měněného parametru nosného signálu. Lze tedy říct, že se jedná o ekvivalenty analogových modulací.

Princip nekvantovaných modulací spočívá ve vzorkování modulačního signálu. Vzorkování je proces, při kterém dochází, vždy po uplynutí vzorkovací periody, k odebrání vzorku z analogového modulačního signálu. Tyto vzorky se poté uchovávají (tato vzorkovací metoda se nazývá Sample and Hold; existují i jiné metody, ale tato je nejběžnější). Zařízení, které vzorkování provádí se nazývá vzorkovač (= vzorkovací obvod).

Důležité je při vzorkování zvolit správnou délku vzorkovací periody (respektive frekvenci vzorkovacího signálu¹), aby nedocházelo k příliš velkému zkreslení a případným ztrátám informace. Podle Shannonova–Nyquistova–Kotělnikovova teorému (často se mu říká jen Shannonův–Kotělnikovův teorém) musí být vzorkovací frekvence nejméně dvakrát vyšší než nejvyšší frekvence obsažená ve vzorkovaném (modulačním) signálu. Řečeno matematicky:

\[ f_{vz} \geq 2 \cdot f_{max} \]

kde $ f_{vz} $ je vzorkovací frekvence a $ f_{max} $ maximální frekvence obsažená ve vzorkovaném signálu.

Obecným problémem nekvantovaných pulzních modulací je náchylnost ke zkreslení způsobenému přítomností rušivých signálů v přenosovém kanále.

Protože jak všichni jistě víme, platí že $ T = \frac{1}{f} $, kde $ T $ je perioda a $ f $ frekvence, a tedy tyto dvě veličiny jsou na sobě závislé.

Pulzně amplitudová modulace (PAM)

PAM je metoda, při které dochází k úpravě amplitudy nosného signálu. Principiálně je velmi jednoduchá (jedná se prakticky o čisté vzorkování) - z modulačního signálu jsou v době vzorkovacích impulzů (vzorkovací signál zde funguje jako nosný) odebírány jeho aktuální hodnoty a ty tvoří výsledný modulovaný signál.

Vlastnost nosného signálu	Mění se
amplituda	ANO
pozice pulzu v čase	NE
střída	NE

PAM má dva typy:

PAM I (1. druhu) - používá přirozené vzorkování, což znamená, že po dobu vzorkovacího pulzu je na výstup přiveden přímo modulační signál (není zde použit Sample and Hold obvod) → modulovaný signál není obdélníkový
PAM II (2. druhu) - používá uniformní vzorkování = je použit Sample and Hold obvod; na výstup je po celou dobu trvání vzorkovacího pulzu přiváděna hodnota, která byla změřena při jeho začátku → modulovaný signál je (za ideálních podmínek) obdélníkový


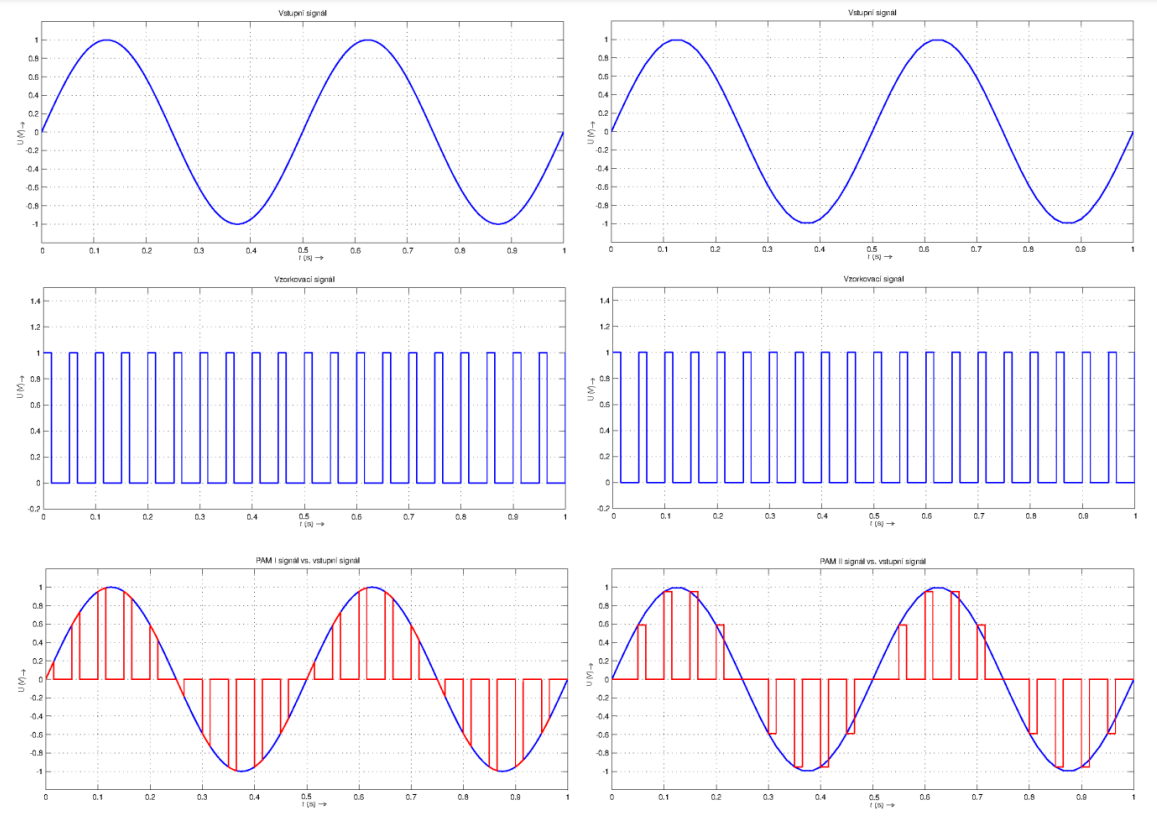obr. 1: PAM (I vlevo, II vpravo)
zdroj: ŠIŠKA, M. Impulzové modulace. Brno: Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, 2013. 101 s. Vedoucí diplomové práce Ing. Radim Číž, Ph.D.

Důležité parametry PAM:

Výška vzorkovacího pulzu $ (D) $
Šířka vzorkovacího pulzu $ (\theta) $
Vzorkovací perioda $ (T_{vz}) $

Z pohledu použití není PAM příliš vhodná pro přenos informací (amplitudové modulace jsou náchylné na rušení). Používá se hlavně jako součást jiných modulačních systémů (např. PCM). Dále také v některých verzích ethernetu a nové verzi sběrnice PCI Express. Též je využívána jednou severoamerickou televizí.

Pulzně šířková modulace (PWM)

Princip PWM spočívá ve změně střídy (= poměr mezi stavem log. 0 a log. 1 v rámci jedné periody (většinou se udává v procentech)) výstupního signálu na základě okamžité hodnoty modulačního signálu. Střída $ (D) $ je dána vztahem $ D = \frac{\tau}{T} $, kde $ \tau $ je doba, po kterou je signál v úrovni log. 1 a $ T $ je perioda signálu.

Činnost spočívá v komparaci modulačního signálu s referenčním pilovým (nebo trojúhelníkovým) signálem z generátoru. V rámci jedné periody, dokud je hodnota modulačního signálu vyšší než hodnota signálu referenčního, má výstupní signál hodnotu log. 1. Jakmile překročí hodnota referenčního signálu hodnotu modulačního, výstupní hodnota se mění na log. 0.


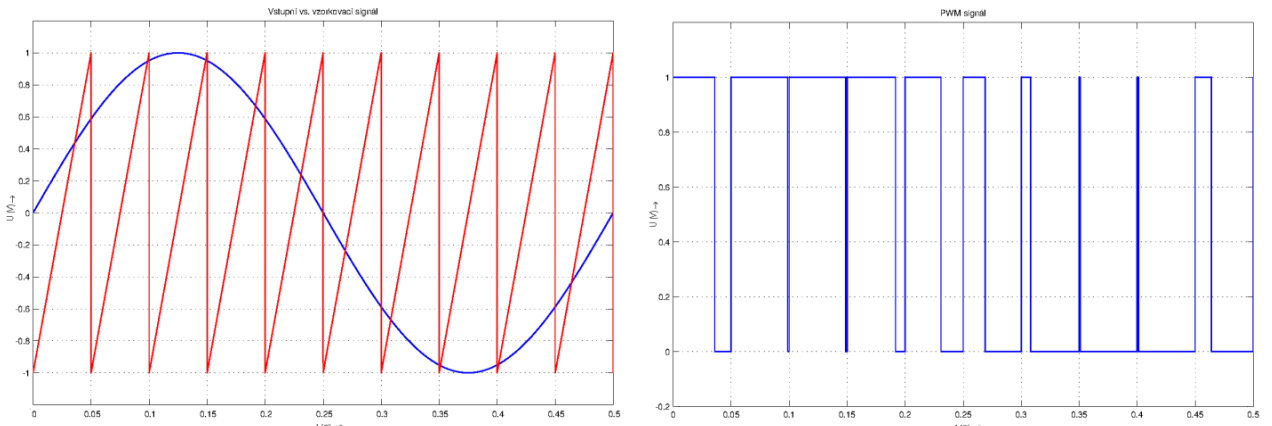obr. 1: PWM (vlevo: červená - pilový referenční signál, modrá - modulační signál; vpravo: modulovaný signál)
zdroj: ŠIŠKA, M. Impulzové modulace. Brno: Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, 2013. 101 s. Vedoucí diplomové práce Ing. Radim Číž, Ph.D.

Vlastnost nosného signálu	Mění se
amplituda	NE
pozice pulzu v čase	NE
střída	ANO

Ve skupině spojitých modulací nemá PWM žádnou obdobu.

TODO přidat vysvětlení, proč PWM funguje

PWM se hojně využívá ve výkonové elektronice pro řízení DC/DC měničů nebo stejnosměrných motorů, servo motorů, ovládání jasu světelných zdrojů nebo také pro řízení otáček ventilátorů.

Velkou výhodou při použití PWM k napájení (např. právě motory) je absence ztrát, ke kterým dochází při klasickém lineárním napájení. To je díky tomu, že tranzistor (který se používá jako spínací prvek) má nejmenší ztráty ve stavu plného otevření a zavření (tedy log. 1 a 0).

Pulzně polohová modulace (PPM)

U PPM odpovídá okamžitá hodnota modulačního signálu poloze impulzu v odpovídající periodě modulovaného signálu. Princip PPM tedy spočívá v posouvání pulzů výstupního signálu úměrně k aktuální hodnotě modulačního signálu, a to buď doprava, pokud je aktuální hodnota vyšší než rozhodovací úroveň (což je většinou 0, tedy aktuální hodnota je kladná), anebo doleva, je-li aktuální hodnota nižší než rozhodovací.

PPM je obdobou fázové spojité modulace.

Vlastnost nosného signálu	Mění se
amplituda	NE
pozice pulzu v čase	ANO
střída	NE


obr. 2: PPM
zdroj: ŠIŠKA, M. Impulzové modulace. Brno: Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, 2013. 101 s. Vedoucí diplomové práce Ing. Radim Číž, Ph.D.

Levý obrázek znázorňuje modulační (modrý) a vzorkovací (červený) signál. Pravý výstupní impulzy odpovídající hodnotě 0 V (červené; slouží jako reference pro lepší představu) a skutečné výstupní hodnoty (modré).

PPM se používá v optických přenosových systémech (optická síť), radio-control systémech (rádiové řízení, např. dronů; pro RC byla původně vytvořena) a pro vesmírnou komunikaci.

Nevýhodou PPM je náročnost implementace, jelikož je nutná synchronizace na straně vysílače a přijímače (obvykle se řeší tak, že jednotlivé pulzy jsou posunuty relativně k sobě navzájem - rozdílová pulzně polohová modulace). Dalším problémem je výcecestné šíření signálu. Pokud k němu dochází (říká se tomu ozvěny), není téměř možné rozpoznat ozvěny od skutečných přenosů → PPM je nepoužitelné.

Kvantované

Kvantované modulace využívají kromě procesu vzorkování ještě kvantování a kódování. Tyto procesy jsou obvykle použity jako postupné kroky.

Kódování je proces převodu kvantovaných hladin jednotlivých vzorků na binární číslo, které je finální produkt modulace.

Běžné kvantované modulace jsou:

Pulzně kódová modulace (PCM)
- Diferenční pulzně kódovaná modulace (DPCM)
- Adaptivní diferenciální pulzně kódová modulace (ADPCM)
Delta modulace (DM)
- Delta-sigma modulace (ΔΣ)
- Adaptivní delta modulace (ADM)

Zdroje

ŠIŠKA, M. Impulzové modulace. Brno: Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, 2013. 101 s. Vedoucí diplomové práce Ing. Radim Číž, Ph.D.
Přispěvatelé Wikipedie, Modulace [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 3. 03. 2022, 11:20 UTC, [citováno 19. 04. 2023] https://cs.wikipedia.org/w/index.php?title=Modulace&oldid=20994654
Přispěvatelé Wikipedie, Pulzně amplitudová modulace [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 30. 01. 2023, 07:47 UTC, [citováno 21. 04. 2023] https://cs.wikipedia.org/w/index.php?title=Pulzn%C4%9B_amplitudov%C3%A1_modulace&oldid=22393152
Přispěvatelé Wikipedie, Pulzně šířková modulace [online], Wikipedie: Otevřená encyklopedie, c2021, Datum poslední revize 8. 08. 2021, 15:40 UTC, [citováno 21. 04. 2023] https://cs.wikipedia.org/w/index.php?title=Pulzn%C4%9B_%C5%A1%C3%AD%C5%99kov%C3%A1_modulace&oldid=20340653
https://robodoupe.cz/2016/pulzne-sirkova-modulace/
http://fyzika.jreichl.com/main.article/view/1358-kodovani-signalu

Řízení motorů

Servomotory, krokové motory, stejnosměrné motory, synchronní a asynchronní pohony. Řízení otáček a točivého momentu. Bez senzorové řízení motorů.

V kostce jde o odeslání signálu / impulsu motoru, přičemž délka onoho impulsu ovlivňuje úhel o nějž se motor pootočí. Pro kontrolovanou a přesně řízenou změnu polohy hřídele (otáčku motoru) využíváme tzv. PWM - Pulse-Width Modulation (Pulzně šířkovou modulaci). PWM řídíme DC motory, serva i krokové motory. Pro krokové motory i DC musíme však využít drivery s externím napájením, které upraví napájecí signál dle řídícího z MCU.

Servo motory, krokové motory a DC motory

Na úvod je třeba říci, že termín servomotor nevypovídá o struktuře motoru jako takového. Servomotory mohou být AC, DC, kartáčové (brushed), bezkartáčové (brushless). Ve většině industriálních robotických systému se využívají právě DC motory.

DC motor

DC motor využívá vinuté cívky (rotoru) jež rotuje v magnetickém poli vytvořeném permanentními magnety nebo vynutím cívky statoru. Pro hladší a účinnější chod rotoru je využit komutátor. Komutátor zajišťuje přívod a přepínání proudu vedených do rotorových cívek tak, aby byla napájena vždy cívka pod aktivním pólem. Komutátor je rozdělen na izolované lamely po nichž se třou kartáče rotoru (grafitové nebo uhlíkové).


obr. 1: DC kartáčové motory - dvoupólový a čtyřpólový
zdroj: Electronics Tutorials: DC Motors [online]. 2014 [cit. 2023-05-13]. Dostupné z: https://www.electronics-tutorials.ws/io/io_7.html

DC brushed & brushless motor

Kartáčové DC motory jsou levné a snadno ovladatelné motory, které využívají kartáčů (z grafitu / uhlíku) jež se třou o komutátor (oddělené kovové lamely připojené na hřídeli rotoru) a nimiž vedou proud, čímž mění polaritu a stator se otáčí. Kartáče jsou připojeny k externímu zdroji napájení (viz např. na videu zde). Jde o to, že opačné póly na statoru a rotoru se přitahují a zároveň (na opačné straně) odpuzují a aby se motor neotočil jen o půl otáčky do mrtvého bodu, kde budou proti sobě opačné póly jež se přitáhly, tak kartáče nabité externě skrze komutátor změní polaritu cívek rotoru a tím pádem se motor otočí úplně.

Brushless motory (bez kartáčů) nemají vinutí na statoru, ale permanentní magnety, které vytváří magnetické pole. Na statoru je vinutí cívkami vytvářející elektromagnetické pole. Jak se otáčí rotor, mění se polarita na jednotlivých cívkách statoru, což vede ke kontinuální rotaci.

Výhody a nevýhody

DC motor brushed: menší počáteční náklady (provoz může být dražší, neboť je třeba měnit kartáče); vyšší spolehlivost; lepší kontrola rychlosti motoru (velikostí napětí)
DC motor brushless: delší životnost, bezúdržbový, vyšší účinnost

Zapojení DC motoru - sériové a paralelní zapojení


obr. 2: Zapojení motorů sériově a paralelně
zdroj: Electronics Tutorials: DC Motors [online]. 2014 [cit. 2023-05-13]. Dostupné z: https://www.electronics-tutorials.ws/io/io_7.html

Seriové


obr. 3: Sériové zapojení cívek
zdroj: YAM, Ian Jonas. Wiring Connection of Direct Current (DC) Motor. Technovation - Technological Innovation and Advanced Industrial Control Technologies [online]. 2013 [cit. 2023-05-15]. Dostupné z: http://ijyam.blogspot.com/2013/11/wiring-connection-of-direct-current-dc.html

Paralelní


obr. 4: Sériové zapojení cívek
zdroj: YAM, Ian Jonas. Wiring Connection of Direct Current (DC) Motor. Technovation - Technological Innovation and Advanced Industrial Control Technologies [online]. 2013 [cit. 2023-05-15]. Dostupné z: http://ijyam.blogspot.com/2013/11/wiring-connection-of-direct-current-dc.html

Krokové motory

Jedná se synchronní brushless motor. Ergo, rotor krokáče tvoří mnoho "zubů" z permanentních magnetů (mohou jich být i stovky) a stator je tvořen mnoha cívkami. Krokový motor se hýbe dle jednotlivých kroků (diskrétně) (na základě počtu magnetů a vynutí). Krokový motor se může otáčet o setiny či desetiny stupně. Např. otočí-li se motor o 360° v průběhu 100 kroků, tak každý krok odpovídá 3.6°. Nejpoužívanější krokové motory se otáčí 200 kroky za otáčku (1 krok = 1.8°).

Použití krokáčů je nasnadě v 3D tiskárnách, ploterech případně robotických systémech s velmi jemnou kontrolou pohybu.

Schéma krokového motoru a princip pohybu


obr. 5: Schéma krokového motoru
zdroj: Electronics Tutorials: DC Motors [online]. 2014 [cit. 2023-05-13]. Dostupné z: https://www.electronics-tutorials.ws/io/io_7.html

Stator krokáče výše má cívky generující elektromagnetické pole, označené ADCB. Pokud povedeme proud do cívek ADCB, krokáč se bude točit na jednu stranu, pro otáčení v protisměru ABCD. Rotor se otočí vždy o krok (step angle).

Krokáč má 6 magnetických zubů a 4 cívky (nabité +-, aby bylo možné realizovat jeden krok). Tedy motor může udělat 24 kroků (6x4), ergo jeden krok je 15° (360 / 24). Teto motor je 4-fázový, právě dle počtu cívek.

Pozici motoru je možné odvodit od počtu impulsů, neboť každý impuls (budeme-li je posílat odděleně -> time-delayed) odpovídá 1 step angle.

Takže, pokud náš motor bude mít jeden step angle 3.6° a budeme-li chtít otočit jej na 216° vůči původní pozici, tak motoru pošleme 60 impulsů (216/3,6).

Dosažení kroku lze několika způsoby:

přidáním zubů na rotor a stator
spínáním více cívek naráz, čímž se rotor dostane do polohy "mezi cívkami" a tím realizuje fragment kroku

Typy krokových motorů

Pasivní krokové motory - Variable Reluctance Motors
Fungují tak, jak je popsáno výše, Rotor je tvořen ocelovými pláty seřazenými za sebou (jakási laminace) a otáčí se na základě působení elektromagnetického pole generovaného cívkami statoru.
Aktivní krokové motory
Rotor je tvořen permanentním magnetem. Točí se opět na bázi působení elektromagnetického pole.
Hybridní krokové motory
Rotor je tvořen magnetem a zuby, které se řadí proti zubům statoru, buď se zarovnají plně proti sobě, nebo jsou zuby rotoru srovnané přesně proti mezerám mezi zuby statoru, nebo jsou vyrovnány do poloviny zubů statoru (viz obrázek).


obr. 6: Hybridní krokový motor
zdroj: Lesics. YouTube. How does a Stepper Motor work? [online]. [cit. 2023-05-15]. Dostupné z: https://www.youtube.com/watch?v=eyqwLiowZiU

Servo motor

Servo motory jsou jakýmsi komplexnějším systémem složeným z těchto komponent: DC motor, micro-controller, poziční sensor, převodovka. Převodovka je napojena přímo na hřídel DC motoru, čímž zvětšuje kroutící moment. Zabudované MCU zpracovává signál z externí řídící jednotky a prostřednictvím impulsu jej předá motoru. Zpětnou vazbu o natočení motoru nám dává potenciometr.

Schéma servo-motoru můžete vidět níže.


obr. 6: Schéma servomotoru
zdroj: Servos explained. Sparkfun: Start something [online]. [cit. 2023-05-15]. Dostupné z: https://www.sparkfun.com/servos

Řízení motoru pomocí PWM

Pulsně-šířková modulace je obšírně rozebírána v otázce č. 3.10.

Servomotory mají na rozdíl od DC většinou omezený rozsah otočení hřídele, byť některé servomotory se mohou otáčet kontinuálně. Obecně se servomotory otáčí o 180°nebo 210°.

V závislosti na délce signálu se hřídel serva otočí pro/proti směru hodinových ručiček. Otočení dle délky signálu ilustruje obrázek níže. Vyšleme-li signál o délce 1,5ms, servo se otočí v protisměru hodinových ručiček o 90° (do neutrální polohy), pošleme-li impuls kratší než 1,5ms, otočí se servo po směru hodinových ručiček opět o 90°. Bude-li délka signálu větší než 1,5ms otočí se hřídel proti směru do polohy 180° (tedy o 90° vůči neutrální poloze).

Konvenční interval mezi impulsy bývá u hobby serva 20ms, tedy MCU pošle 50 signálů za vteřinu.


obr. 7: Rotace servomotoru
zdroj: SCHERZ, Paul a Simon MONK. Practical electronics for inventors. Fourth edition. New York: McGraw-Hill Education, [2016]. ISBN 978-1-25-958754-2.

Synchronní a asynchronní motory

Synchronní motory jsou takové motory, u nichž se rotor otáčí stejnou rychlostí s jakou jsou zapojovány cívky statoru. Frekvence otáčení rotoru je synchronní k frekvenci zapínání.

Asynchronní motory se vyznačují tím, že rotor se točí s pomaleji, než je zapínání/frekvence pouštění proudu do cívek.

Jen pro zajímavost - kroutící moment může dodávat ASM jen tehdy, točí-li se rotor pomaleji, než se točí magnetické pole statoru. Tomuto se říká SKLUZ.

\[S = \frac {n_1 - n_2}{n_1} * 100\]

S - skluz
$n_1$ - otáčky magnetického pole statoru
$n_2$ - otáčky rotoru

Skluz bývá mezi 2-10 %.

Třífázové ASM jsou nejrozšířenější motory. Lehké na údržbu a levné. Používají se tam, kde je třeba robustní pohon (průmyslové dopravníky, pohony výhybek na dráze, jezdící schody...).

Zdroje

https://www.youtube.com/watch?v=-J1Km7h38U8&t=227s
https://www.electronics-tutorials.ws/io/io_7.html
https://www.analogictips.com/pulse-width-modulation-pwm/
https://www.sparkfun.com/servos
SCHERZ, Paul a Simon MONK. Practical electronics for inventors. Fourth edition. New York: McGraw-Hill Education, [2016]. ISBN 978-1-25-958754-2.
https://cs.wikipedia.org/wiki/Asynchronn%C3%AD_motor
https://en.wikipedia.org/wiki/Stepper_motor

FPGA systémy

FPGA systémy - postup syntézy, jazyky VHDL, Verilog. Vlastnosti popis požití pro řízení. Principy číslicových filtrů.

Všechny programovatelné součástky se souhrnně označují PLD (Programmable Logic Device). Jedná se o integrované obvody, které umožňují konfigurovat jejich logickou funkci a propojení po výrobě. Na rozdíl od hradel, registrů a jiných číslicových obvodů (které mají z výroby pevně danou funkci) musí být PLD před použitím nejprve naprogramováno. PLD je možné podle vnitřní struktury rozdělit na:

klasické PLD - typ, který zahrnuje jednoduchou logiku, jako jsou AND, OR a NOT brány, a registrů. Nejznámější příklady jsou PAL (Programmable Array Logic) a PLA (Programmable Logic Array).
komplexní PLD - pokročilejší typ, který obsahuje více logických bloků, registrů a propojovacích matic. Umožňuje větší flexibilitu a zpracování složitějších logických funkcí. Typické příklady jsou XC9500 od společnosti Xilinx a MAX od společnosti Altera (nyní Intel).
FPGA (Field Programmable Gate Array) - nejvýkonnější a nejrozšířenější typ PLD. Obsahuje velké množství logických bloků a programovatelných propojek, které umožňují vytvoření komplexních digitálních obvodů a systémů. Umožňuje vývojářům implementovat a rekonfigurovat vlastní logické funkce a propojení a je široce využíván v oblasti digitálního návrhu a vývoje hardwaru.

FPGA obvod

Typickou strukturu obvodu FPGA znázorňuje následující obrázek.


obr. 1: FPGA obvod

Bloky označené IOB (Input/Output Block) představují vstupně-výstupní obvody pro každý pin. Tyto bloky obvykle obsahují registr, budič, multiplexer a ochranné obvody.
Bloky LB (Logic Block) představují vlastní programovatelné logické bloky. Všechny bloky mohou být různě propojeny globální propojovací maticí.

Rozeznáváme dva základní typy FPGA podle uložení konfigurace:

FPGA s volatilní konfigurací, které ukládají konfigurační informace do paměťových buněk typu SRAM.
FPGA s nevolatilní konfigurací, které ukládají konfigurační bity typicky ve flash paměti, EEPROM, nebo tzv. antifuses (antipojistky).

Syntéza FPGA

Syntéza FPGA je proces transformace vyššího úrovně popisu hardwaru na nízkoúrovňovou implementaci, vhodnou pro konkrétní FPGA čip.

Proces: popis hardwaru ve vyšším jazyce (např. VHDL nebo Verilog) je převeden na logické funkce a obvody, které realizují požadovanou funkčnost. V tomto kroku jsou aplikovány optimalizace a transformace k dosažení požadovaného výkonu a efektivity. V dalším kroku je třeba zajistit konverzi těchto funkcí a obvodů na netlist, využívající prostředky konkrétního FPGA a zajistit jejich "optimální" rozmístění a propojení.

Jazyky VHDL, Verilog

Hlavními jazyky pro programování obsahu hradlových polí jsou dnes VHDL a Verilog.

VHDL je nezávislý na platformě a umožňuje popsat hardware na různých úrovních abstrakce, od nejvyššího (strukturální) po nejnižší (úrověň hradel). Je silně typovaný. Má prostředky pro popis paralelismu, konektivity a explicitní vyjádření času.

# Konečný automat ve VHDL
signal stav: integer := 0;
process (clk, reset)
begin
    if reset = '1' then
        state <= 0;
        y <= '0';
    elsif (clk'event and clk = '1')
        case state is
            when 0 =>
                state <= 0;
                y <= '1';
            when 1 =>
                state <= 2
                y <= '0';
...
            when others =>
                state <= 0;
                y <= '0';
        end case;
    end if;
end process;

clk'event and clk='1' reprezentuje vzestupnou hranu hodinového signálu
y je výstup konečného automatu.

Jazyk Verilog má odlišnou syntaxi. Když VHDL je založen na strukturovaném programování a používá klíčová slova jako "entity", "architecture" a "process" pro popis hardware, Verilog je založen na přístupu popisu chování a struktury a používá klíčová slova jako "module", "always" a "assign" pro popis hardwaru. Souhrn rozdílů je znázorněn na následujícím obrázku.


obr. 1: Verilog vs VHDL

Číslicové filtry

Filtr pro zpracování signálu představuje model, kterým modelujeme nějaký systém (skutečný, virtuální) popisující relace mezi vstupem a výstupem filtru (tzv. přenosová charakteristika). Filtr pro zpracování signálu (zkráceně jen filtr) je využíván v oborech regulace (automatizace), číslicové zpracování signálu, elektronika (radiotechnika), atd. Existuji analogové filtry pro zpracování analogového signálu a číslicové filtry.

Číslicové filtry jsou elektronické obvody nebo systémy, které se používají k úpravě a zpracování digitálního signálu. Tyto filtry pracují s diskrétním časem, ve kterém jsou signály reprezentovány vzorky.

Číslicové filtry mají za úkol změnit frekvenční charakteristiky signálu, například filtrováním nežádoucích frekvenčních složek nebo zvýrazněním určitých frekvenčních pásem. Mohou se také použít pro úpravu amplitudy, fáze nebo času signálu.

Existují dva základní typy číslicových filtrů:

IIR (Infinite Impulse Response) - filtry s konečnou impulsní odezvou, které mají zpětnou vazbu mezi výstupem a vstupem. To znamená, že výstup filtru závisí nejen na aktuálním vstupním vzorku, ale také na předchozích výstupních vzorcích.
FIR (Finite Impulse Response) - filtry s nekonečnou impulsní odezvou, které neobsahují zpětnou vazbu. To znamená, že výstup filtru závisí pouze na aktuálním vstupním vzorku a předchozích vstupních vzorcích.

Jak FIR, tak IIR filtr se dá zrealizovat pomocí tří základních bloků, tyty bloky jsou zobrazeny na následujícím obrázku.


obr. 1: Základní realizační bloky pro sestavení číslicových filtrů

Jedná se o:

Sčítací člen - sečte dva signály
Násobička - vynásobí daný signál konstantou
Zpožďovací člen - zpoždění o jeden krok

Číslicové filtry se používají v různých aplikacích, včetně komunikace, zpracování zvuku, zpracování obrazu a mnoha dalších oblastí, kde je potřeba digitálního zpracování signálu. Jsou také důležitou součástí digitálního zpracování signálů (DSP) a jsou implementovány pomocí algoritmů a hardwaru jako číslicové signálové procesory (DSP procesory), FPGA nebo ASIC (Application-Specific Integrated Circuit).

Zdroje

Přispěvatelé Wikipedie, Programovatelné hradlové pole [online], Wikipedie: Otevřená encyklopedie, c2023, Datum poslední revize 5. 01. 2023, 20:02 UTC, [citováno 17. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Programovateln%C3%A9_hradlov%C3%A9_pole&oldid=22306362
https://pediaa.com/what-is-the-difference-between-verilog-and-vhdl/
Přispěvatelé Wikipedie, Filtr (zpracování signálu) [online], Wikipedie: Otevřená encyklopedie, c2021, Datum poslední revize 17. 06. 2021, 08:59 UTC, [citováno 17. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Filtr_(zpracov%C3%A1n%C3%AD_sign%C3%A1lu)&oldid=20075258
HAMPL, L. Číslicová filtrace - výukové simulace. Brno: Vysoké učení technické v Brně, Fakulta elektrotechniky a komunikačních technologií, 2016. 65 s. Vedoucí bakalářské práce Ing. Soňa Šedivá, Ph.D. https://core.ac.uk/download/pdf/44402309.pdf

Modelování a simulace vestavných (embedded) systémů

Přímé vkládání programů z matematických systémů (MATLAB, Mahematica, apod.) do vývojových desek.

Motivace

Modelování je proces návrhu embedded systému jak po stránce hardwarové, tak i softwarové. Pokud máme návrh, můžeme realizovat sestrojení prototypu. Avšak ne vždy si můžeme být jistí tím, že software bude na prototypu fungovat podle našich představ. Je proto vhodné otestovat náš softwarový návrh v takovém prostředí, které nás nebude stát fyzické zdroje. Můžeme náš návrh vzít a simulovat jak program běží ve virtuálním prostředí. Více o modelování a návrhu embedded systému se lze dočíst v otázce Metody testování vestavných(embedded) systémů, převážně v kapitole Delta-W model.


obr. 1: Příklad modelování embedded systému za pomocí Simulinku
Dostupné z: https://en.wikipedia.org/wiki/Simulink

Simulace nám dává možnost simulovat to, jak bude daná aplikace běžet na daném systému, bez nutnosti fyzické existence cílového zařízení, přičemž je poté možné výkonný kód do daného typu zařízení nahrát / vložit.

Více o principu emulace a simulace lze nalézt v otázce Simulace a emulace vestavných systémů.

Simulace vs emulace

Mezi simulací a emulací je rozdíl, ač se oba dva tyto termíny používají zaměnitelně. Emulace umožňuje vytvořit virtuální zařízení, které má stejné schopnosti, jako originál. Emulátory jsou psané v low-level programovacích jazycích, jako je například Assembler. Překládají strojový kód, aby co nejvíce odpovídal chodu daného zařízení, jak hardwarově, tak softwarově, což často vede k pomalému chodu tohoto zařízení. Příkladem může být emulátor Android telefonu (SDK) při programování mobilních zařízení. Jejich hlavní využití je při debuggingu hardware.

Na druhou stranu simulátor běží nad operačních systémem jako aplikace. Jeho účelem je pouze navodit pocit toho, že pracujeme s nativním zařízením. Nereprezentuje hardware, pouze uživatelské prostředí. Používá se pro simulování chování a konfigurace nativního zařízení. Využití nalezne také při testování aplikací vyvíjených pro simulované zařízení.

Vkládání programů do vývojových desek

V dnešní době se používají software, které využívají tzv. Model-based design. Jde o proces modelování za pomocí některého z modelovacích jazyků. Tímto způsobem můžeme vytvořit model jak celého embedded systému, tak i obslužného programu. Tyto programy kromě vytváření modelů často umožňují simulaci, automatické generování kódu a verifikaci. Jsou tedy nedílnou součástí postupu vývoje (a samozřejmě testování) embedded systémů, o kterém si lze více přečíst v otázce Metody testování vestavných (embedded) systémů, převážně v kapitole Delta-W model.

Existuje velké množství takových programů, my si tu uvedeme ty nejznámější:

Matlab: Používá Simulink, což je placené rozšíření k placenému programu Matlab
Wolfram SystemModeler: Placený software, umožňuje trial po dobu 30 dní
Modelica: open software, zdarma

Ne vždy je nutné kód obslužného programu psát. Pokročilé modelovací prostředí, jako je například Simulink, nám umožní namodelovat systém i jeho chování v grafické podobě, ze které je toto prostředí schopné vygenerovat kód, který lze poté zkompilovat a spustit na cílovém zařízení.

Než však nahrajeme kód do vývojové desky, je nejdříve nutné ji připojit. Povětšinou se to dělá za pomocí COM portů, což jsou sériové porty, kterými připojíme zařízení, do něhož chceme kód nahrát.

Existuje i možnost vkládání programů přes síť. Tuto možnost nabízí například Simulink, společně s Raspberry, kde je možnost nahrát na dálku do zařízení program v podobě spustitelného souboru.

Nahráním programu do vývojové desky se přepíše obsah paměti. Drtivá většina vývojových desek (snad jen s výjimkou Raspberry) umožňuje mít v sobě pouze jeden spustitelná program.

Procesorová jednotka na vývojové desce poté zpracovává nahraný kód v podobě instrukcí. Často je tomu tak v nekonečné smyčce, která umožňuje programovat automatizované činnosti.

Zdroje

Programming the World with Arduino and Mathematica. Ian Johnson. [online] @2014 [citováno: 12.05.2023]
Dostupné z: https://community.wolfram.com/groups/-/m/t/315748
Virtual Device (Emulator and Simulator) vs. Real Device: What is the Difference?. SauceLabs. [online] @2022 [citováno: 12.05.2023]
Dostupné z: https://saucelabs.com/resources/blog/mobile-device-emulator-and-simulator-vs-real-device
Can I upload Arduino Code written in MATLAB using MATLAB Arduino Support Package?. Mathworks. Walter Roberson. [online] @2015 [citováno: 12.05.2023]
Dostupné z: https://www.mathworks.com/matlabcentral/answers/257423-can-i-upload-arduino-code-written-in-matlab-using-matlab-arduino-support-package

Simulace a emulace vestavných systémů

Postupy pro simulování a emulování reálných procesů v použitých zařízeních. Druhy emulátorů a jejich rozhraní (SPI, JTAG, inside emulátory). Příprava procesorů pro emulaci.

Simulace vs Emulace

Je rozdíl mezi simulací a emulací procesů, ač se oba dva tyto termíny používají zaměnitelně. Emulace umožňuje vytvořit virtuální zařízení, které má stejné schopnosti, jako originál. Emulátory jsou psané v low-level programovacích jazycích, jako je například Assembler. Překládají strojový kód, aby co nejvíce odpovídal chodu daného zařízení,jak hardwarově, tak softwarově, což často vede k pomalému chodu tohoto zařízení. Příkladem může být emulátor Android telefonu při programování mobilních zařízení. Jejich hlavní využití je při debuggingu hardware.

Na druhou stranu simulátor běží nad operačních systémem jako aplikace. Jeho účelem je pouze navodit pocit toho, že pracujeme s nativním zařízením. Nereprezentuje hardware, pouze uživatelské prostředí. Používá se pro simulování chování a konfigurace nativního zařízení. Využití nalezne také při testování aplikací vyvíjených pro simulované zařízení.

Co je to proces?

Procesem v embedded systémech myslíme program, v případě emulace poté program společně s HW, který vykonává jednotlivé kroky popsané programem.

Definice: série kroků nebo operací za účelem dosažení určitého cíle.

Postup simulace procesu

Definujeme cíl simulace. Cílem může být například optimalizace výkonu, analýza latence, ověřování nových funkcionalit atd. Prostě chceme proces (program) otestovat.
Identifikujeme proměnné systému: Musíme zjistit, které části celého systému proces ovlivňují. Může se jednat o vstupní/výstupní signály, výpočetní zatížení, spotřebu energie apod. Toto je důležité pro vytvoření adekvátního modelu.
Vytvoření modelu: Na základě identifikovaných proměnných vytvoříme matematický nebo abstraktní model systému.
Specifikujeme vstupní data: Musíme určit vstupní data, která představují reálné signály - scénáře jež mohou nastat. Při simulaci můžeme systému tyto data předat vytvořením simulační sady dat, nebo vytvořením skriptu pro generování dat.
Implementujeme simulaci: Vytvoříme z abstraktního/matematického modelu model v simulačním prostředí (například Simulink) nebo nahrajeme výkonný kód do vývojové desky.
Spustíme simulaci: Můžeme použít různé sady vstupů pro otestování různých scénářů.
Sesbíráme a analyzujeme data: Sesbíráme výstupní data, která odpovídají výsledkům vůči cílům simulace.

Postup emulace procesu

Definujeme cíl emulace: Cíle může být například ověření správnosti návrhu systému, testování nových funkcionalit, simulaci reálných podmínek atd.
Identifikujeme klíčové komponenty: Musíme rozpoznat klíčové komponenty systému, který chceme emulovat, jako jsou například mikrokontroléry, senzory, aktuátory atd.
Vytvoříme emulační prostředí: Vytvoříme prostředí, které je schopné emulovat reálné podmínky, ve kterých bude embedded systém provozován. Může jít o testovací laboratoř, nebo software v podobě emulační platformy.
Implementujeme emulační software: Jedná se o vytvoření softwaru, který simuluje chování hardware. To zahrnuje vytvoření emulačního kódu, který simuluje jednotlivé funkce a reakce našeho embedded systému.
Nakonfigurujeme vstupy: Musíme určit vstupní data, která představují scénáře jež mohou nastat a podmínky, ve kterých je systém provozován. To může zahrnovat emulaci senzorů, vstupů od uživatele, komunikačních rozhraní a dalších vstupních kanálů.
Spustíme emulaci: Spustíme emulaci a budeme sledovat její průběh. Můžeme měnit vstupy na základě scénářů, jež chceme sledovat.
Sesbíráme a analyzujeme vstupní data: Na základě cílů emulace sesbíráme data, která popisují chování embedded systému.

Druhy emulátorů

Emulátory se v základu dělí na dvě částí

hardwarové emulátory:
- Jedná se o emulátory, které jsou schopné vytvořit přesnou kopii hardware, včetně jeho procesoru a paměti. Nejznámějšími nástroji pro hardwarovou emulaci jsou virtualizační nástroje VMware, nebo VirtualBox. Emulují celý systém, popřípadě prostředí, ve kterém systém operuje.
softwarové emulátory:
- Jedná se o emulátory, které umožňují spustit program v prostředí, které je pro něj nativní. Můžeme takto spouštět programy, které nejsou na novějších zařízeních spustitelné. Emulují pouze software, jež na zařízení běží.
- Zároveň tyto emulátory umožňuji komunikaci dvou zařízení, které spolu nejsou kompatibilní, například pomocí JTAG sběrnice. Procesory využívají JTAG k umožnění přístupu k emulačním/debugovacím funkcím. Pokud bychom chtěli upravovat flash paměť nějakého zařízení, můžeme k tomu použít emulátor flash paměti, který připojíme pomocí SPI sběrnice.

Další využití JTAG sběrnice

Využití JTAG sběrnice je dále převážně v debuggingu, protože je možné díky této sběrnici přistupovat k operační paměti připojeného zařízení, nebo dokonce k samotným instrukcím mikrokontroléru/procesoru. Vlastně umožňuje low-level programování zařízení, ke kterému ho připojíme, můžeme s ním programovat flash paměť, FPGA, nebo EEPROM.

Zajímavost: Microsoft u svých konzolí XBox pravidelně banuje účty uživatelů, kteří používají JTAG sběrnici konzole.

Dále můžeme tyto emulátory dělit podle toho, jak se liší způsobem využití a prostředím, ve kterém jsou využívány.

Terminálové emulátory
- Simuluje klasický terminál (ten se sestává z displaye a klávesnice a představoval rozhraní pro ovládání počítače člověkem). Terminálové emulátory slouží ke stejnému účelu. Např. klasické terminálové aplikace v Linuxu.
Tiskárnové emulátory
- Simulují firmware tiskáren. Spousta těchto emulátorů je zaměřena na HP tiskárny kvůli velkému množství software pro HP tiskárny. Emulátor je schopný pracovat se softwarem/firmwarem vyvíjeným pro tiskárny.
Herní (konzolové) emulátory
- Umožňují emulovat hardware dané herní konzole a spouštět na ní software v podobě her pro tuto konzoli.
Celosystémové emulátory
- Tyto emulátory emulují vše, včetně CPU, chipsetu, BIOS, periferie a přerušení. Tyto emulátory jsou těžké vytvořit. Důvodem je nutnost naprostého odproštění od systému, na kterém emulátor běží.
CPU emulátory
- Jedná se o software, který emuluje fyzické CPU. Pro každou instrukci vykonanou emulátorem, je vykonaná identická instrukce na hostujícím CPU. Interpert, který sleduje kód vykonávaný emulovaným programem je nejjednodušším typem CPU emulátoru. Umožňuje spouštět programy, které jsou psané pro jinou architekturu CPU, než je ta přítomna na nativním zařízení.
Serverové emulátory
- Emulují zařízení, na kterém běží serverová aplikace. Chod serveru je simulován za pomocí umělé zátěže.
Síťové emulátory
- Testování sítě v laboratoří je síťová emulace. Často obsahuje ztráty packetů či latenci pro navození pocitu reálného prostředí.
Mobilní emulátory
- Mobilní emulátory simulují hardware a software zařízení na hostujícím zařízení. Například emulátor Android.

Emulace sběrnic

Pokud emulujeme nějaký systém, je možné emulovat i jednotlivé sběrnice, které tento systém využívá. Emulace pak zahrnuje princip fungování jednotlivých sběrnic.

Příprava procesorů pro emulaci

K emulačním schopnostem procesoru můžeme přistoupit pomocí JTAG sběrnice. Čtením a zápisem do instrukčního registru můžeme poté skrze procesor emulovat chování jiného systému.

Zdroje

Simulation. Wikipedia: The Free Encyclopedia. [online] @2023 [citováno 13.05.2023].
Dostupné z: https://en.wikipedia.org/wiki/Simulation
What Are Emulators? Definition, Working, Types, and Examples. Chiradeep BasuMallick. [online] @2023 [citováno 13.05.2023].
Dostupné z: https://www.spiceworks.com/tech/devops/articles/what-are-emulators/
What’s the Difference Between Hardware and Software Emulation?. Richard Reynolds. [online] @2022 [citováno 13.05.2023].
Dostupné z: https://history-computer.com/whats-the-difference-between-hardware-and-software-emulation/
JTAG. Wikipedia: The Free Encyclopedia. [online] @2022 [citováno 13.05.2023].
Dostupné z: https://en.wikipedia.org/wiki/JTAG
PROMJet SPI. EmuTec. [online] @2023 [citováno 13.05.2023].
Dostupné z: https://www.emutec.com/flash_spi_emulator_hardware_promjet.php
JTAG Boundary-Scan Benefits FAQ. Corelis. [online] @2023 [citováno 13.05.2023].
Dostupné z: https://www.corelis.com/education/corelis-faq/
What is JTAG and how can I make use of it?. XJTAG. [online] @2023 [citováno 13.05.2023].
Dostupné z: https://www.xjtag.com/about-jtag/what-is-jtag/

Metody testování vestavných (embedded) systémů

základní přístupy, vývojové modely (vodopád, spirálový, V-model, W-model, Delta-W model), modelování vestavných (embedded) systémů

Zaměřit se hlavně na Delta-W model, kde se řeší paralelní vývoj/testování SW a HW.

Motivace

Vývoj embedded systému se skládá ze dvou odlišných a na sobě téměř nezávislých částí. První je navrhnutí a sestrojení hardware, často v podobě vývojové desky - výrobní cyklus. Tato deska je poté hozena softwarovému týmu, který tiše doufá, že je vše funkční a problémy, které se vyskytnou jsou čistě softwarového rázu. Problémem zde je fakt, že při vývoji software na chybném hardware se hardwarové problémy mohou jevit jako softwarové. Vývojový tým tedy může hledat problémy na špatných místech a neuvědomit si, že je potřeba opravit samotný hardware.

Testování hardware je poslední částí vývojového cyklu HW. Stejně tak testování software je poslední částí vývojového cyklu SW.

Testování hardware zahrnuje:

testování jednotlivých periferií (senzory, kamery, tlačítka...)
Testování robustnosti (otřesy, vibrace)
testování firmware

Tento okruh se bude dále zaobírat testováním software na vytvořeném hardware v embedded systémech. Je nutné si uvědomit, že při testování se vždy může objevit možnost toho, že se jedná o hardwarový problém.

Proč testujeme?

Nalezení bugů:
- snížení rizika jak pro uživatele, tak pro společnost, jež zařízení vyvíjí
- čím dříve bug najdeme, tím levnější je jeho oprava
Snížení náročnosti vývoje a ceny údržby:
- chyby mají tendenci se hromadit
- pokud netestujeme včas, může se stát, že nebudeme dělat nic jiného než opravovat chyby
Zlepšení výkonu:
- testování může identifikovat úseky, které zpomalují chod celého řešení
- úpravou těchto úseků můžeme dosáhnout značného zrychlení

Základní přístupy

Základní přístupy zahrnují dva způsoby testování:

Funkcionální testy (Black-box testing)
Testy pokrytí (White-box testing)

Základní princip testů je ten, že se snažíme naše řešení rozbít, zničit. Snažíme se dokázat, že aplikace nefunguje. Děláme cokoliv (náhodné vstupy stylem mlácení hlavou do klávesnice, přetěžování vstupů...), o čem jako programátoři víme, že aplikaci uškodí.

Black-box testing

Jedná se o analogii k unit testům. Testujeme jednotlivé funkcionality, přičemž nás zajímá pouze vstupní set parametrů a odpovídající výstup, který můžeme porovnat s očekávaným výstupem. Nezajímá nás to, jak fungují algoritmy, které zajišťují jednotlivé funkcionality.

Díky tomu, že black-box testy testují jednotlivé funkcionality na základě vstupních parametrů můžeme psát tyto druhy testů zároveň s vývojem aplikace.

Příklady black-box testů:

Stress test:
- záměrně přetěžujeme vstupní kanály, vyrovnávací paměti, systémy pro správu paměti, apod.
Boundary value tests:
- testujeme vstupy, které mají být v určitém rozmezí
- pokud máme vstup, který může být jen v intervalu <0,2>, tak tam například zkusíme poslat hodnotu 3
Exception tests:
- testy, které si kladou za cíl vyvolat výjimku, nebo přerušit program
Performance tests
- testy měřící rychlost řešení
Náhodné testy:
- testování založené na zkušenostech z předchozího vývoje podobných řešení

White-box testing

Nevýhodou black-box testů je fakt, že často neotestují všechen výkonný kód. Testy pokrytí se proto snaží zajistit, že každý rozhodovací bod v programu, každé tvrzení, každá výsledná větev, je otestována alespoň jednou.

Testy pokrytí předpokládají, že programátor plně zná implementaci software. Má tedy možnost "podívat se dovnitř" (na rozdíl od black-box testů). Podoba těchto testů plně závisí na řešení implementace, není je proto možné psát paralelně s vývojem.

Z pohledu embedded systémů se jedná o nejdůležitější testy, protože nám umožní pokrýt velkou část aplikace a tím zamezit neočekávaných chybám jež se mohou objevit v budoucnu, popřípadě vyloučit, že se jedná o chyby softwarového rázu.

Příklady white-box testů:

Statement coverage: testy pokrývající to, že se každé tvrzení v programu vykoná alespoň jednou
Branch coverage: testy pokrývající to, že se každé větvení programu (if - > true/false) vykoná alespoň jednou
Condition coverage: pokrytí podmínek. Testy zajišťují, že podmínka je otestována na co nejvyšší možné spektrum různých hodnot (aneb co se stane, pokud porovnávám dvě čísla a pošlu tam float)

Vývojové modely (SDPM)

Vývojové modely lze najít pod zkratkou SDPM (Software development process models). Jejich cílem je definovat jednotlivé fáze vývoje počínaje studiem problému až po údržbu kompletního řešení. Celému procesu, který model popisuje se říká SDLC (System deployment life cycle).

Dále budou popsány existující SDLC modely.

Waterfall model

Tento model byl představen v roce 1970 Winstonem Roycem. Skládá se z 5 částí a vývojář musí splnit předchozí část, aby se mohl posunout na další. Model je tedy sekvenční/lineární.


obr. 1: Waterfall model
zdroj: https://www.javatpoint.com/software-engineering-waterfall-model

Popis částí:

Analýza požadavků a specifikací: Vývojář si sedne se zákazníkem a společně projdou, co by měl systém umět, jaký by měl mít výkon a popřípadě jaká bude podoba uživatelského rozhraní. Výsledkem je dokument Software Requirement Specification (SRS).
Design: Tato část se zabývá vytvořením architektury aplikace na základě SRS dokumentu. Tato architektura již umožní programování v určitém jazyce. Výsledkem je opět dokument, tentokrát pod názvem Software Design Document (SDD).
Implementace a Unit testy: V této části je implementován design na základě SDD. Pokud je SDD kompletní, tak jde tato část hladce, neboť se řídí čistě tím, co je v SDD.
Integrace a testování systému: Tato část je velmi důležitá, neboť kvalita výsledného produktu závisí na efektivitě testů prováděných v této části.
Údržba: Udržování systému v chodu za pomocí spravování vzdálených úložišť. Tato část může být vykonávána i uživatelem samotným, který udržuje systém v chodu.

Výhody:

jednoduchá implementace
požadavky jsou pevně dané a není potřeba počítat s tím, že se budou měnit
začátek a konec každé fáze je pevně daný

Nevýhody:

rizikový faktor je vyšší, není tedy vhodné použít tento model pro komplexní projekty
model se nedokáže adaptovat na změny v požadavcích
je těžké vracet se k předchozím fázím
Testování je děláno v pozdějších fázích -> je těžké odhadnout náročnost a rizika projektu

Kdy použít waterfall model?

Požadavky jsou pevně dané a neměnné
Projekt je malý
Používané nástroje a technologie je neměnná
Potřebné zdroje jsou připraveny k použití

Spirálový model

Jedná se o model, který kombinuje předchozí lineárně sekvenční postup s možností opakované iterace. Software je vytvářen pomocí série několika vydání. Prvotní série mohou mít podobu náčrtu na papíře, nebo prototypu. S dalšími sériemi stoupá komplexita vytvořeného systému. Každá série je cyklus tvořený ze 4 částí.


obr. 2: Spiral model
zdroj: https://www.javatpoint.com/software-engineering-spiral-model

Popis částí:

Identifikace: Začátkem každého cyklu je identifikace toho, co je účelem tohoto cyklu, identifikace způsobů, jak dosáhnout vytyčených cílů.
Odhadnutí rizik: Cílem je odhadnutí možných problémů na základě vnímání rizik v dané fází (cyklu).
Development a validace: Implementace strategií, jež potlačí nejasnosti a rizika. Může zahrnovat věci jako jsou benchmarking, simulace a prototypování.
Plánování: Projekt je zhodnocen a na základě tohoto hodnocení se určí, zdali cyklus zopakovat, nebo se přesunout na další fázi (sérii).

Výhody:

Zaměření na analýzu rizik
Snadná implementace pro velké projekty

Nevýhody:

Drahý model na použití
Analýza rizik vyžaduje expertízu
Není vhodný pro malé projekty

Kdy použít Spirálový model?

Požadavky jsou nejasné a komplexní
Projekt je velký
Změny mohou nastat kdykoliv
Projekt má vyhrazené velké finanční zdroje

V-model

Tento model je také označovaný jako verifikační a validační model. Používá stejnou sekvenční logiku pro jednotlivé fáze jako Waterfall model. Rozdíl je v tom, že testy jsou plánované paralelně vůči fázi, ve které se projekt nachází.


obr. 3: V-model
zdroj: https://www.javatpoint.com/software-engineering-v-model

Model se skládá ze dvou cyklů:

verifikace: statická analýza bez spouštění kódu.
validace: dynamická analýza, testování je prováděno spouštěním kódu. Kontroluje, zdali jsou splnění očekávání a požadavky klienta.

Verifikace:

Analýza business požadavků: Zjištění požadavků klienta
Design systému: Zhodnocení a vytvoření hrubého nástinu na základě požadavků klienta.
Design architektury(High-level-design): Návrh jednotlivých modulů systému, vztahů mezi moduly, závislostí, struktury tabulek, letmý popis funkcionality modulů
Design modulů (Low-level-design): Rozvržení jednotlivých modulů a jejich zjednodušení na základní moduly.
Programování: Na základě potřeby a designu projektu je zvolen vhodný programovací jazyk, v této fázi prochází řešení řadou code-review pro zajištění maximálního výkonu.

Validace:

Unit testy: Jejich návrh je vytvořen už ve fázi designu modulů, ale implementace probíhá až po programování. Účelem je zjistit bezchybnost jednotlivých nezávislých modulů.
Integrační testy: Jejich návrh je vytvořen už ve fázi designu architektury. Testy ověřují, zdali jednotlivé skupiny modulů dokáží správně komunikovat mezi s sebou.
Systémové testy: Jejich návrh je vytvořen už ve fázi designu systému. Jsou vytvořeny business týmem klienta a zaručují, že jsou naplněna očekávání klienta.
Acceptance testing: Jejich návrh je vytvořen už ve fázi analýzy business požadavků. Zahrnují testování software v prostředí klienta. Mohou odhalit problémy, jež souvisí s jiným software, který je využívaný klientem, nebo problémy s výkonem v uživatelském prostředí.

Výhody:

Jednoduchý na pochopení
Design testů se provádí před samotným programováním
Šíření chyb mezi jednotlivými fázemi je zabráněno

Nevýhody:

Není flexibilní
Nehodí se na komplexní projekty
Software je vytvářen společně s implementací, není tedy možnost prototypu
Pokud se objeví nějaké změny, je potřeba upravit již vytvořené testovací dokumenty

Kdy použít V-model?

požadavky jsou srozumitelné a dobře definované
projekt je malý až střední
počáteční zdroje jsou připravené s možností získat další zdroje v budoucnu

W-model

Jedná se o model vycházející z V-modelu. Účelem je možnost testování již od prvního dne započetí vývoje.


obr. 4: W-model. Každá část verifikace (oranžová), je testována validací (černá)
zdroj: https://www.javatpoint.com/software-engineering-v-model

Z obrázku je patrné, že W-model řeší nedostatek V-modelu. v podobě možnosti testovat systém a kód při jeho vývoji (nikoliv až po něm). Princip tohoto modelu zůstává jinak shodný s V-modelem.

Výhody:

možnost testovat a vyvíjet zároveň

Nevýhody:

komplexní a tím pádem složitý na implementaci
špatně se odhaduje, kolik zdrojů alokovat do vývoje systému, povětšinou je prvotní odhad příliš malý
Testování má stejnou váhu jako jiné aktivity

Kdy použít W-model?

Máme mnoho různých aktivit, jež je třeba implementovat
Pokud nestačí V-model

Delta-W-model

Jedná se o úpravu W-modelu tak, aby vyhovoval požadavkům na vývoj embedded systémů, tedy tomu, že je potřeba vyvinout nejen software, ale i zařídit vhodný hardware.

Skládá se ze dvou částí, požadavků a vytváření. Testování obou částí je zajištěno. V případě požadavků jde o kontroly (review), v případě vytváření jde o testy.

Konceptuálně se jedná o W-model s přidaným paralelismem (vyvíjíme jak HW tak SW)


obr. 5: Delta-W model
zdroj: https://dspace5.zcu.cz/bitstream/11025/623/1/r5c4c2.pdf

Stejně jako v případě W-modelu jde testování ruku v ruce s vývojem. Premisa zůstává stále stejná (vyvíjíme a testujeme zároveň, nejdříve navrhujeme, poté implementujeme)

První části ze dvou je tedy zjištění požadavků. Tyto požadavky zároveň hodnotíme ve formě review testů.


obr. 6: Návrhová část Delta-W modelu
zdroj: https://dspace5.zcu.cz/bitstream/11025/623/1/r5c4c2.pdf


obr. 7: Hodnocení požadavků (review) část Delta-W modelu
zdroj: https://dspace5.zcu.cz/bitstream/11025/623/1/r5c4c2.pdf

Poté, co máme zrevidované detailní návrhy jak softwarové, tak hardwarové části, je možné započít implementaci


obr. 8: Implementační část Delta-W modelu
zdroj: https://dspace5.zcu.cz/bitstream/11025/623/1/r5c4c2.pdf

S tím, jak implementujeme jednotlivé části, je zároveň i testujeme.


obr. 9: Testování implementace podle Delta-W modelu
zdroj: https://dspace5.zcu.cz/bitstream/11025/623/1/r5c4c2.pdf

Díky testování je poskytována zpětná vazba, která nám umožní vyladit nedostatky.


obr. 10: Příklad výroby hardware při použití Delta-W modelu
zdroj: https://dspace5.zcu.cz/bitstream/11025/623/1/r5c4c2.pdf

Modelování vestavných (embedded) systémů

K modelování embedded systémů se často využívají modelovací jazyky. Jedná se vizuální (grafické) jazyky, které nám umožňují lépe přiblížit danou skutečnost. Těchto jazyků je velké množství, uvedeme pár příkladů.

UML - standart pro modelování software
EXPRESS - pro modelování dat
Behavioral Trees - používané pro modelování konkurence, nedeterminismu, synchronizace a komunikace
Vývojový diagram - pro schématické znázornění určitého algoritmu

Embedded systémy sestávají ze dvou složek

hardware
software

Z definice embedded systému plyne, že takový systém je dělaný za konkrétním účelem. (pokud nebereme v potaz sofistikované vývojové desky typu Arduino či Raspberry). Návrh systému by měl tedy sestávat z:

Vytvoření modelu hardwarového řešení
Vytvoření modelu softwarového řešení

Vytvoření návrhů nám umožní znovupoužitelnost a hlavě přehlednost ohledně toho, z jakých komponent se daný embedded systém skládá. K tomuto účelu se nejlépe hodí vývojový model Delta-W.

Více o modelování embedded systémů lze najít v otázce Modelování a simulace vestavných systémů.

Zdroje

Embedded Software Testing Basics. Embedded Staff. [online] @2011 [citováno: 12.05.2023]
Dostupné z: https://www.embedded.com/the-basics-of-embedded-software-testing-part-1/
V-Model. Javapoint. [online] @2021 [citováno: 12.05.2023]
Dostupné z: https://www.javatpoint.com/software-engineering-v-model
Waterfall model. Javapoint. [online] @2021 [citováno: 12.05.2023]
Dostupné z: https://www.javatpoint.com/software-engineering-waterfall-model
V-Model. Javapoint. [online] @2021 [citováno: 12.05.2023]
Dostupné z: https://www.javatpoint.com/software-engineering-v-model
What is V-model and W-model in Software Testing Testbytes. [online] @2017 [citováno: 12.05.2023]
Dostupné z: https://www.testbytes.net/blog/v-model-and-w-model-software-testing/
W-development model extension for embedded system design. Department of Microelectronics, Faculty of Electrical Engineering and Communication, BUT, Brno, Technická 10, Brno. D. Jaroš, M. Pavlík.[online] @2011 [citováno: 12.05.2023]
Dostupné z: https://dspace5.zcu.cz/bitstream/11025/623/1/r5c4c2.pdf
Modelling Language Wikipedia: The Free Encyclopedia. [online] @2023 [citováno: 12.05.2023]
Dostupné z: https://en.wikipedia.org/wiki/Modeling_language

Státní závěrečné zkoušky - Aplikovaná informatika

Fungováním neuronových sítí jako celku se dále zaobírá okruh Základní modely neuronových sítí.