Syntaktická analýza a LL gramatiky

Tento okruh vychází ze znalosti okruhu Bezkontextové gramatiky a jazyky.

Syntaktická analýza, neboli parsing má největší uplatnění při návrhu programovacích jazyků. Rozlišujeme syntaktická a sémantická pravidla.

Syntaktická pravidla se vyjadřují pomocí přepisovacích pravidel bezkontextové gramatiky.

Pro syntaktickou analýzu je třeba kromě určení, zda w ∈ L(G) (je řetězec w slovo generované jazykem L, jež popisuje gramatika G?), také najít odvození S ⇒ w, tj. určit, z jakých syntaktických celků se w skládá (klíčové slovo, operátor, číslo, ...).

Syntaktický analyzátor bere jako vstup řetězec tokenů, které jsou získány skrze lexikální analýzu a porovná tento řetězec s přepisovacími pravidly. Výstupem je parsovací strom.

Postup syntaktické analýzy
obr. 1: Postup syntaktické analýzy
dostupné z: https://elearning.jcu.cz/pluginfile.php/279723/mod_resource/content/9/prezentace.pdf

Tento okruh se zaobírá syntaktickou analýzou shora dolů, tedy od kořene stromu, až k jeho listům, kde se nacházejí terminály. Syntaktická analýza zdola nahoru naopak funguje na principu toho, že začínáme u terminálů a výsledkem je startovní symbol (kořen).

  • Syntaktickou analýzu shora dolů lze provést následujícími způsoby:
    • Analýza rekurzivním sestupem (Analýza hrubou silou, obsahuje backtracking)
    • Analýza ne-rekurzivním sestupem (bez backtrackingu, LL(1) parser nebo také predikativní parser)
Rozdělení syntaktických analyzátorů
obr. 2: Rozdělení syntaktických analyzátorů
dostupné z: https://elearning.jcu.cz/pluginfile.php/279723/mod_resource/content/9/prezentace.pdf

Základním způsobem, jež samozřejmě má své nevýhody, je provést analýzu hrubou silou - analýzu všech možností.

Pro připomenutí:

  • Gramatika G je popsána uspořádanou čtveřicí (V, T, S, P)
    • V: množina všech neterminálních symbolů (proměnných)
    • T: množina všech terminálních symbolů (abeceda)
    • S: počáteční symbol jež patří do množiny V
    • P: konečný set přepisovacích pravidel

Analýza všech možností

  1. vezmeme všechna pravidla tvaru S → x1, kde x1 ∈ (V ∪ T) a x1 může být řetězec složený z terminálů a neterminálů
  2. pro všechna taková x1 vezmeme všechna pravidla tvaru A1 → x2, kde A1 je první proměnná (neterminál) v x1 (nejvíc vlevo)
  3. pokud se některou cestou dostaneme až ke slovu w, máme hledané (levé) odvození
    • dospějeme­li k řetězu, z něhož určitě nelze w odvodit, větev ukončíme
    • tento přístup se též nazývá analýza hrubou silou
    • jde o typ analýzy shora dolů

Nevýhody

  • hledání nemusí skončit
    • pokud řetězec w nepatří do jazyka L generovaného gramatikou G, můžeme vytvářet stále delší cesty a nikdy nedospět k cíli -> nemůžeme předem s jistotou určit, jestli w do jazyka patří, či nikoliv
    • příklad:
      • hledáme odvození slova aabb
      • gramatika je popsaná přepisovacím pravidlem: S → SS | aSb | bSa | λ
      • tento problém odstraníme tak, že gramatiku upravíme aby neobsahovala žádná vypouštěcí (S -> λ), či jednotková (A -> B) pravidla
      • po úpravě dostaneme: S → SS | aSb | bSa | ab | ba
      • algoritmus je poté schopen pro každý řetězec w rozhodnout, zdali patří do jazyka, či nikoliv
      • počet k tomu nutných odvození je poté maximálně dvojnásobek délky hledaného slova, tedy maximálně 2|w|
  • exponenciální složitost
    • v každém kroku algoritmu můžeme v nejhorším případě použít všechna přepisovací pravidla
    • s rostoucí velikostí w tedy roste složitost algoritmu až exponenciálně
    • důvodem je, že u analýzy hrubou silou předem nevíme, jaké přepisovací pravidlo vybrat
    • složitost tohoto algoritmu může dosahovat až O(n!)

Shrnutí: Přepisovací pravidla, jež popisují bezkontextový jazyk generovaný bezkontextovou gramatikou umožňují odvození řetězce hrubou silou. Tento přístup je však velice neefektivní a časově náročný, kde algoritmus sází na vysokou výpočetní sílou procesoru. Pro zlepšení algoritmické složitosti (pokud možno získání lineární složitosti) můžeme použít jiný druh parsování, jako je například zde rozebíraný predikativní parser.

Pro další postup je potřeba gramatiku upravit do tzv. normálních forem (pokud jsme to již neudělali pro její zjednodušení dříve).

  • Chomskyho normální forma (CNF)
  • Greibachové normální forma (GNF)

Motivace: Nechť L je bezkontextový jazyk neobsahující λ. Potom existuje bezkontextová gramatika, která generuje L a přitom neobsahuje žádné zbytečné proměnné a produkce, λ-­produkce ani jednotkové produkce. Pokud máme bezkontextový jazyk, který neobsahuje λ­, pak je možné ho upravit do jedné z normálních forem.

Úprava přepisovacích pravidel

  • odstranění λ ­produkcí
  • odstranění jednotkových produkcí
  • odstranění zbytečných produkcí a proměnných
    • produkce jsou zbytečné, pokud jsou stejné jako jiné produkce
    • proměnná je zbytečná, pokud stejného výsledků dosáhneme odvozením skrze jinou proměnnou

Proč ale chceme upravovat přepisovací pravidla, aby vyhovovali jedné ze dvou norem a navíc jsme odstranili λ ­produkcí?. V kontextu syntaktické analýzy chceme tuto gramatiku převést na LL gramatiku, abychom pomocí ní mohli sestrojit predikativní parser.

LL gramatiky

Jedná se o bezkontextové gramatiky, které neobsahují levou rekurzi a jsou jednoznačné.

Levá rekurze:

  • S -> aAb
  • A -> Aa - tady se nachází levá rekurze, toto není LL gramatika
  • A -> λ

Jednoznačná gramatika:

Taková gramatika, kdy pro každé slovo w generované jazykem popsaným touto gramatikou existuje pouze jeden derivační strom, tedy pouze jedna sada odvození skrze přepisovací pravidla.

Využití LL gramatik:

Následující přepisovací pravidlo můžeme přesně určit, pokud se podíváme na omezenou část vstupního řetězu (příští symbol + pevný počet dalších). První L: vstup čteme odleva, druhé L: děláme levé odvození. LL(k): díváme se na k vstupních symbolů, speciálně u LL(1) jen na následující.

Toto vede k sestrojení predikativního parseru.

Predikativní parser

Řada programovacích jazyků je definována pomocí LL gramatik a jejich kompilátory využívají LL analyzátory. Pro LL(k) gramatiku lze vytvořit prediktivní parser, který je v každém kroku analýzy schopen vybrat správnou produkci (přepisovací pravidlo) na základě prvních k terminálů v dosud nezpracované části vstupního řetězu.

Parser tohoto docílí na základě parsovací tabulky. Ta mu říká, jaké pravidlo má vybrat na základě k vstupních symbolů.

Analýza tímto způsobem spadá do kategorie parsování rekurzivním sestupem. Predikativnímu parseru jež využívá LL(1) gramatiku se také říká LL(1) parser.

Příklad parsovací tabulky, kde k = 1
obr. 3: Příklad parsovací tabulky, kde k = 1
dostupné z: https://elearning.jcu.cz/pluginfile.php/279723/mod_resource/content/9/prezentace.pdf

Sestavení predikativního parseru se staví na dvou funkcích:

  • FIRST
  • FOLLOW

Funkce FIRST

Funkce FIRST(x) jednoznačně určuje, který další znak následuje při odvození x.

  • L -> aB
  • L -> c
  • L -> λ
  • funkce FIRST(L) = FIRST {a,c,λ}

Funkce FOLLOW

Funkce FOLLOW(x) říká, jaký symbol následuje za neterminálem x, který odvozujeme. Do funkce FOLLOW automaticky spadá prázdný řetězec.

  • L -> aBa
  • funkce FOLLOW(B) = FOLLOW {$,a}

Na základě těchto funkcí poté můžeme sestavit parsovací tabulku, která nám umožní určit, jakou produkci (přepisovací pravidlo) vybrat.

Sestavení parsovací tabulky
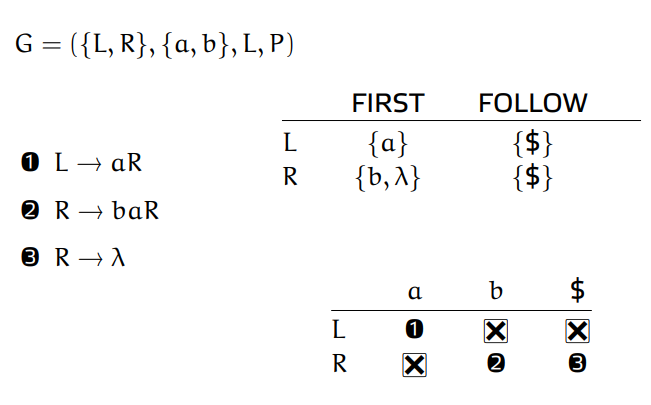obr. 4: Sestavení parsovací tabulky
dostupné z: https://elearning.jcu.cz/pluginfile.php/279723/mod_resource/content/9/prezentace.pdf

Zdroje