Kombinační a sekvenční logické obvody
Kombinační a sekvenční logické obvody, formální popis logických obvodů booleovskými funkcemi a konečnými automaty.
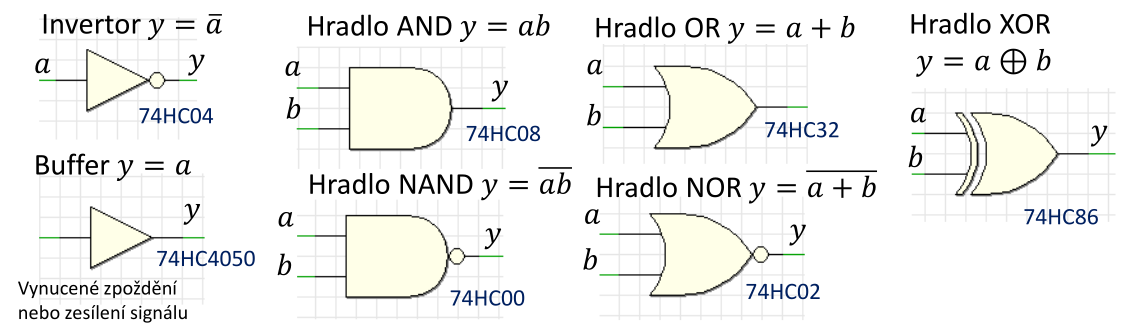
Základem kombinačních i sekvenčních obvodů jsou logická hradla. Z těch se výše zmíněné skládají.
 |
|---|
obr. 1: Běžná logická hradla (uvedené identifikátory 74HCxx označují běžně dostupné integrované obvody s těmito hradly) |
| zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019. |
Popis booleovskými funkcemi
Booleovská proměnná je taková proměnná, která může nabývat pouze dvou hodnot, a to 0 a 1.
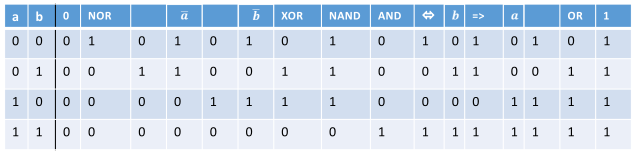
Booleovská funkce je taková funkce, která přijímá jako vstupy a vrací jako výstupy pouze booleovské proměnné. Platí, že pro \(n\) booleovských proměnných existuje \( 2^{2^n} \) booleovských funkcí (např. pro 2 proměnné máme celkem 4 kombinace vstupů, kterým odpovídá 16 funkcí).
 |
|---|
| obr. 2: Boolovská funkce dvou proměnných |
| zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019. |
Vzhledem k tomu, že logické obvody pracují pouze s booleovskými proměnnými (jejich vstupy a výstupy) a obsahují logická hradla (ta reprezentují logické operace), můžeme je považovat za elektronické formy booleovských funkcí a tedy je pomocí nich popisovat.
Pravdivostní tabulka
Základní pomůckou pro reprezentaci logických obvodů pomocí booleovských funkcí je pravdivostní tabulka. Ta obsahuje sloupce pro všechny vstupní i výstupní proměnné a řádky pro všechny kombinace hodnot vstupních proměnných. Např. následující tabulka pro funkci \( y = a + b \).
| a | b | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Úplné normální formy
Z pravdivostní tabulky vychází další důležitý pojem a také další krok, kterým jsou úplné normální formy. Máme dvě a jsou definovány takto:
- Úplná normální disjunktní forma (ÚNDF) - součet (disjunkce) mintermů (pouze ze řádků, kde je výstup roven
1)- minterm - součin (konjunkce) všech proměnných v řádku (ty, které mají hodnotu
1, jsou přímé, s hodnotou0negované); tedy pro \( a, b, c = 0, 1, 0\) to bude \( \neg a \cdot b \cdot \neg c \)
- minterm - součin (konjunkce) všech proměnných v řádku (ty, které mají hodnotu
- Úplná normální konjunktivní forma (ÚNKF) - součin (konjunkce) maxtermů (pouze ze řádků, kde je výstup roven
0)- maxterm - součet (disjunkce) všech proměnných v řádku (ty, které mají hodnotu
0, jsou přímé, s hodnotou1negované); tedy pro \( a, b, c = 0, 1, 0\) to bude \( a + \neg b + c \)
- maxterm - součet (disjunkce) všech proměnných v řádku (ty, které mají hodnotu
Pro výše uvedenou tabulku by NF vypadali takto:
- ÚNDF - \( y = (\neg a \cdot b) + (a \cdot \neg b) + (a \cdot b) \)
- ÚNKF - \( y = a + b \)
Minimalizace
Úplné normální formy jsou sice popisem odpovídajících obvodů, ale zpravidla nejsou popisem ideálním. Abychom dosáhli ideálního, tedy co nejmenšího popisu, musíme je minimalizovat. K tomu můžeme využít následující metody:
- algebraická minimalizace - úprava výrazu využitím zákonů booleovy algebry (poměrně náročné)
- Karnaughovy mapy - postup zde (doporučuji)
- algoritmus Quine-McCluskey
Kombinační obvody
Kombinační obvody jsou takové logické obvody, u kterých aktuální stav výstupů závisí pouze na okamžitém stavu vstupů, nikoliv an předchozích stavech (není zde žádná paměť).
Půlsčítačka
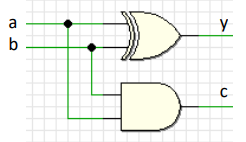
Velmi jednoduchý obvod, který je schopen sečíst dvě jednobitová čísla. Omezením je, že neumí přijímat carry bit z nižšího řádu (to je problém, když děláme vícebitové sčítačky - řetězení).
 |
|---|
| obr. 1: Schéma půlsčítačky |
| zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019. |
Význam jednotlivých vstupů a výstupů:
a- vstupní bitb- vstupní bity- výstupní bit (výsledek)c- carry bit (symbolizuje přetečení do vyššího řádu)
Pravdivostní tabulka
| a | b | y | c |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Booleovské funkce
\[ y = a \oplus b \\ c = a \cdot b \]
Úplná sčítačka
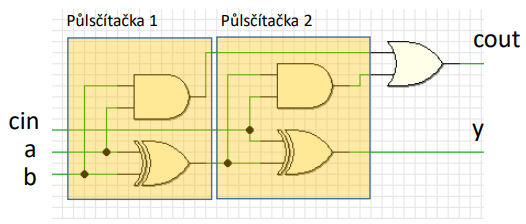
Stejná jako půlsčítačka, ale umí přijímat carry bit z nižšího řádu.
 |
|---|
| obr. 2: Schéma úplné sčítačky |
| zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019. |
Význam jednotlivých vstupů a výstupů:
a- vstupní bitb- vstupní bitcin- carry bit z předešlého řáduy- výstupní bit (výsledek)cout- výstupní carry bit (symbolizuje přetečení do vyššího řádu)
Pravdivostní tabulka
| a | b | cin | y | cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Booleovské funkce
\[ y = a \oplus b \oplus c_{in} \\ c = a \cdot b + (a \oplus b) \cdot c_{in} \]
Vícebitová sčítačka
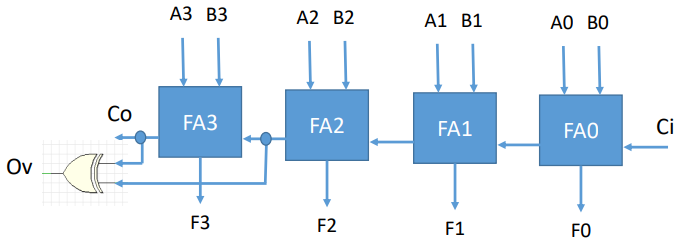
Jedná se o zřetězení jednobitových plných sčítaček.
 |
|---|
| obr. 3: Schéma čtyřbitové sčítačky |
| zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019. |
Význam jednotlivých vstupů a výstupů:
A0...3- vstupní bityB0...3- vstupní bityCi- carry bit z předešlé sčítačky (je-li nějaká)F0...3- výstupní bit (výsledek)Ov- identifikátor přetečení, pro čísla v doplňkovém kódu
Multiplexor
Multiplexor (často zkracovaný jako mux) funguje jako elektronický přepínač. Tím je myšleno, že za pomoci řídicích vodičů vybírá jeden ze vstupů, a ten přivádí na výstup. Např. máme čtyřvstupový mux, tedy máme dva řídicí vodiče a podle toho, jaká hodnota je na ně přivedena (viz pravdivostní tabulka) se jeden ze vstupů přivede na výstup.
Opakem je demultiplexor (demux), který dělá přesný opak - pomocí řídicích vstupů určujeme, na který výstup přepneme vstup (ten je jeden).
 |
|---|
| obr. 4: Schéma muxu |
| zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019. |
Význam jednotlivých vstupů a výstupů:
A...D- vstupy, mezi kterými přepínámeS- řídicí vodiče (červeně označené číslo udává jejich počet)Y- výstup
Pravdivostní tabulka
Pro čtyřvstupový mux. X zde znamená, že na hodnotě nezáleží.
| A | B | C | D | S1 | S2 | Y |
|---|---|---|---|---|---|---|
| X | X | X | X | 0 | 0 | A |
| X | X | X | X | 0 | 1 | B |
| X | X | X | X | 1 | 0 | C |
| X | X | X | X | 1 | 1 | D |
Posuvy
Bitové posuvy se provádějí tak, že před každý výstup je předřazen jeden mux, který přepíná mezi odpovídajícím vstupem a vstupem na vedlejší pozici (podle toho, kam posuv směřuje). Všechny muxy (pro všechny bity) mají společné řízení (= přepínání mezi normálním výstupem, nebo posuvem).
 |
|---|
| obr. 5: Levý posuv, pravý posuv |
| zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019. |
Komparátor
Porovnává hodnoty vstupů a podle typu upravuje výstup. Typ odpovídá operaci, kterou provádí, tedy: =, < a >. Výstup má hodnotu podle toho, jestli je splněna podmínka daná operací.
 |
|---|
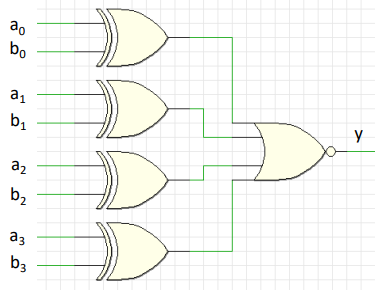
| obr. 6: Schéma komparátoru '=' (4 b) |
| zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019. |
Význam jednotlivých vstupů a výstupů:
a0...3- vstupní bityb0...3- vstupní bityy- výstup (výsledek)
Porovnává se vždy odpovídající dvojice bitů, tedy např. a0 s b0.
Pravdivostní tabulka
By byla vzhledem k počtu vstupů dosti velká a lze ji jednoduše odvodit ze zapojení či booleovské funkce, nebude zde tedy uvedena.
Booleovské funkce
Pro typ =.
\[ y = \neg (a_0 \oplus b_0 + ... + a_n \oplus b_n) \]
Kde \( n \) je počet bitů komparátoru (respektive počet dvojic vstupů).
Násobička
Násobička je soustava \( n^2 \) sčítaček (kde \( n \) je počet bitů jednoho vstupu - činitele), které pracují sériově (tedy postupně → dochází k poměrně velkému zpoždění). Výstup má \( 2 \cdot n \) bitů.
Ne všechny procesory mají násobičku (a tedy instrukci pro násobení). Kde chybí, je nutné násobení provádět opakovaným sčítáním a bitovými posuvy (pomocí kódu v jazyce symbolických adres).
 |
|---|
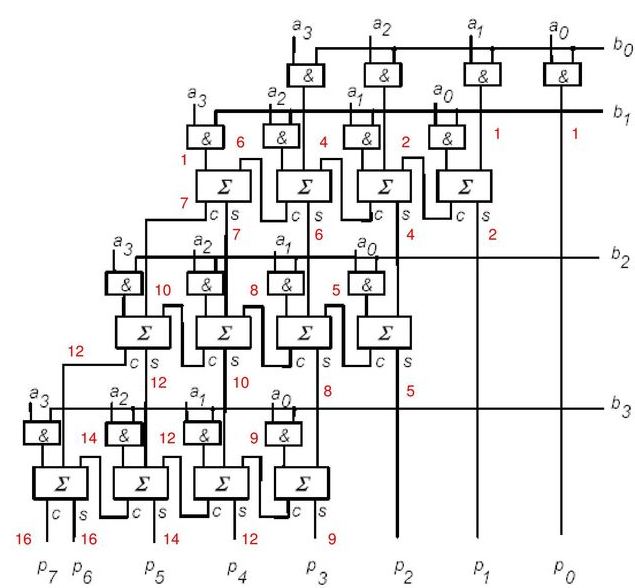
| obr. 7: Schéma násobičky (4 b); každý řádek je jedna sčítačka |
| zdroj: Násobičky, Boothovo překódování: Demonstrační cvičení 7 [online]. [cit. 2023-05-16]. Dostupné z: https://docplayer.cz/17659319-Nasobicky-boothovo-prekodovani-demonstracni-cviceni-7.html |
Význam jednotlivých vstupů a výstupů:
a0...3- vstupní bity prvního činiteleb0...3- vstupní bity druhého činiteleP0...7- výstupní bity (výsledek)
Sekvenční obvody
Sekvenční obvody, na rozdíl od kombinačních, pracují s předešlým stavem, jsou tedy schopny udržovat hodnotu v čase.
Pro práci se sekvenčními obvody je nutné nejprve vysvětlit, co je to tzv. hodinový signál. Jedná se o digitální (nespojitý jak v čase, tak v hodnotě) signál s pevně danou frekvencí a obvykle střídou 50% (to však není pravidlo). Sekvenční obvody jej využívají k informování o tom, kdy mají vykonat svou činnost.
Jeho frekvence udává rychlost činnosti daného obvodu (např. u PC mluvíme o rychlosti procesoru).
R-S klopný obvod
Synchronní hladinový R-S KO (klopný obvod) je nejjednodušším synchronním KO. Další KO se z něj odvozují. Funguje jako dočasná paměť (uchovává hodnoty na výstupu, do příchodu nového pulzu).
- synchronní zde znamená, že využívá hodinový signál (může být i asynchronní = bez hodinového signálu).
- hladinový znamená, že vstupní hodnoty se mohou měnit po celou dobu, co je CLK v log.
1(alternativou jsou hranové KO, ty jsou však konstrukčně náročnější)
 |
|---|
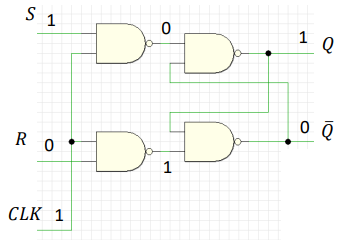
| obr. 8: Schéma synchronního hladinového R-S KO |
| zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019. |
Pravdivostní tabulka
X znamená, že na hodnotě nezáleží. Q a Q (negované) znamená předešlou hodnotu (tedy že nedošlo ke změně) = paměťová funkce.
| CLK | R (reset) | S (set) | Q | Q (negované) |
|---|---|---|---|---|
| 0 | X | X | Q | Q (negované) |
| 1 | 0 | 0 | Q | Q (negované) |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | nepredikovatelný | nepredikovatelný |
Poslední řádek je tzv. zakázaný stav, který by neměl nikdy nastat (výstupy jsou totiž nepredikovatelné). Často se přidávají ochrany, aby se mu zabránilo.
D klopný obvod
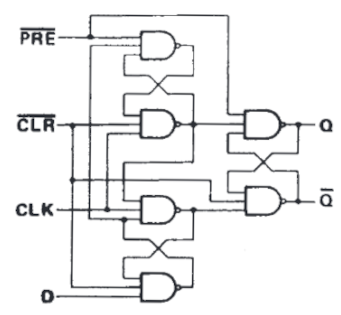
Vylepšený R-S KO (dostaneme jej tak, že na vstup R přivedeme negovanou hodnotu S; zde popsaná varianta má však změn více). Používá se jako jednobitová paměť (hodí se k tomu lépe než R-S).
 |
|---|
| obr. 9: Schéma hranového D KO |
| zdroj: DUAL D-TYPE EDGE TRIGGERED FLIP-FLOPS WIDTH PRESET AND CLEAR, datasheet, Texas Instruments Incorporated, 1988. |
Význam jednotlivých vstupů a výstupů:
PRE- preset - nastavíQna log.1(je asynchronní, tedy pracuje bez ohledu na hodiny), používá se k inicializaciCLR- clear - nastavíQna log.0(je také asynchronní), rovněž se používá k inicializaciCLK- hodinový signálD- datový vstup (při hodinové1se přenese naQ)Q- výstupQ (negované)- negovaný výstup
Pravdivostní tabulka
X znamená, že na hodnotě nezáleží. Q a Q (negované) znamená předešlou hodnotu (tedy že nedošlo ke změně) = paměťová funkce.
| CLK | PRE (negované) | CLR (negované) | D | Q | Q (negované) |
|---|---|---|---|---|---|
| X | 0 | 1 | X | 0 | 1 |
| X | 1 | 0 | X | 1 | 0 |
| 0 | 0 | 0 | X | Q | Q (negované) |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
Registry
Jednobitový registr se synchronním zápisem a asynchronním nulováním
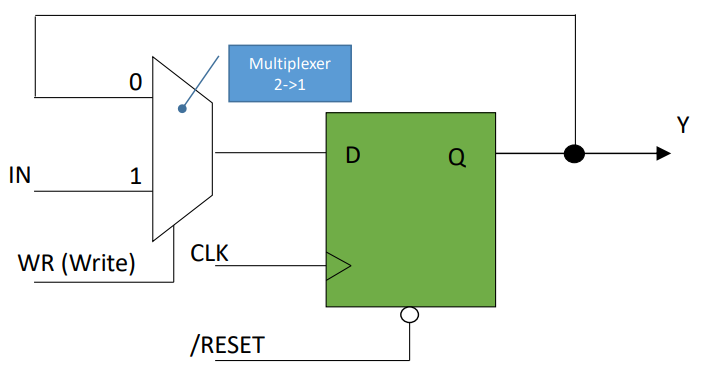
Jedná se o D KO doplněný o mux, který přepíná mezi aktuálním výstupem a vstupem (novou hodnotou). K přepínání dochází na základě hodnoty vstupu write (avšak jen ve chvíli kdy dojde k log. 1 na CLK).
 |
|---|
| obr. 10: Jednobitový registr se synchronním zápisem a asynchronním nulováním |
| zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019. |
Význam jednotlivých vstupů a výstupů:
IN- vstupWR- write - povoluje zápis aktuální vstupní hodnoty na výstupCLK- hodinový signálRESET- vynuluje uloženou hodnotu (je negovaný)Y- výstup
Vícebitový (paralelní) registr
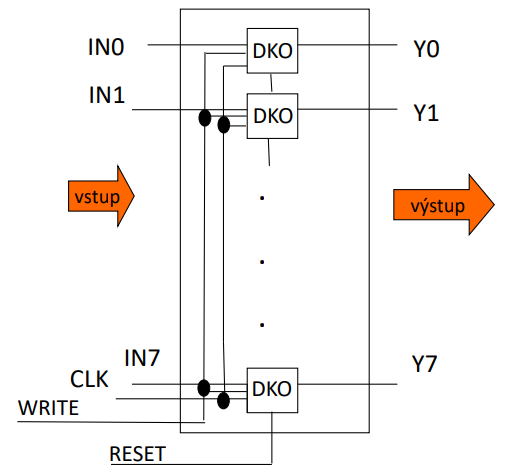
Jedná se o více jednobitových registrů, které mají společné hodiny a WR. Takto si můžeme představit registry v CPU.
 |
|---|
| obr. 11: Osmibitový paralelní registr |
| zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019. |
Posuvný registr
Slouží k serializaci a deserializaci dat.
 |
|---|
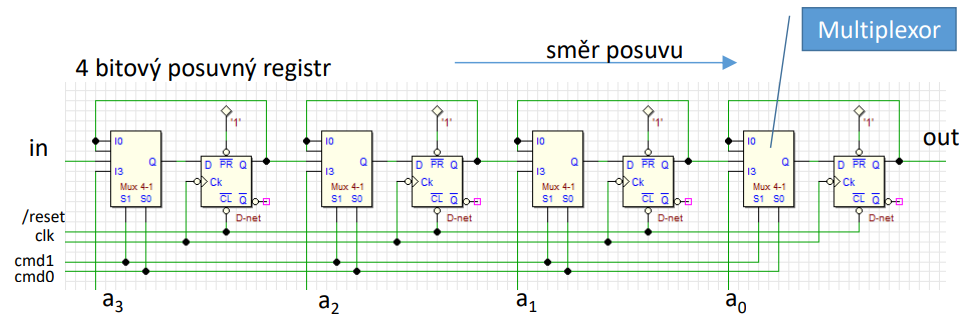
| obr. 121: Čtyřbitový posuvný registr |
| zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019. |
Význam jednotlivých vstupů a výstupů:
IN- sériový vstup (používá se pro postupné přikládání hodnoty; při deserializaci)a0...3- paralelní vstupy (pro okamžité přiložení hodnoty; pří serializaci)reset- úvodní nastavení (negované)clk- hodinový signálcmd0,1- slouží k nastavení aktivního vstupu (0, X- beze změny;1, 0- sériový;1, 1- paralelní)OUT- sériový výstup (ještě by zde měly být paralelní výstupy - za každým KO)
Popis konečnými automaty
Sekvenční obvody lze též popsat pomocí konečných automatů. Jejich činností je totiž přijímat vstupy a na jejich základě podávat výstupy, což je s KA shodné.
Práce s takovými KA je shodná s klasickými KA. Jediným rozdílem je, že potřebujeme binárně zakódovat vstupy a výstupy (můžeme pracovat jen s booleovskými proměnnými).
Zdroje
- Přispěvatelé Wikipedie, Kombinační obvod [online], Wikipedie: Otevřená encyklopedie, c2020, Datum poslední revize 23. 06. 2020, 08:32 UTC, [citováno 16. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Kombina%C4%8Dn%C3%AD_obvod&oldid=18753069
- SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. 2019.
- Přispěvatelé Wikipedie, Bistabilní klopný obvod [online], Wikipedie: Otevřená encyklopedie, c2022, Datum poslední revize 5. 11. 2022, 14:10 UTC, [citováno 16. 05. 2023] https://cs.wikipedia.org/w/index.php?title=Bistabiln%C3%AD_klopn%C3%BD_obvod&oldid=21839873