Číselné soustavy

Převody číselných soustav, základní operace ve dvojkové soustavě. Kódování znaků v počítači, reprezentace čísel se znaménkem a čísla v plovoucí řádové čárce.

Rozlišení soustav a historický zápis čísel

Číselná soustava nám charakterizuje způsob reprezentace čísla. Rozlišujeme dva hlavní druhy číselných soustav, dle způsobu určení jeho hodnoty:

  1. Nepoziční
  2. Poziční

Nepoziční

Hodnota číslice není dána polohou v dané sekvenci číslic. Neobsahují v mnoha případech hodnotu pro 0 a záporná čísla. Zápis komplexnějších čísel je poměrně dlouhý.

  • zářezy na holi (zářezy, které po určitém počtu přeškrtneme), jak počítání týdnů ve věznici :-)
  • římské číslice
  • egyptské číslice
  • řecké číslice (alfabeta)

Římské číslice, I až III dle prstů na rukou. Dále dle rčení: Ivan Vedl Xénii Lesní Cestou Do Města.

Tedy: I, V, X, L, C, D, M \(\iff\) 1, 5, 10, 50, 100, 500, 1000

Poziční

Charakteristické základem neboli bází (eng. radix). Radixem je kladné celé číslo definující maximální počet číslic, které jsou v dané soustavě k dispozici.

V přednáškách jsme používali místo r, písmeno Z, jako Základ.

Poziční soustavy se kromě jedničkové nazývají také polyadické - číslo v nich napsané, lze vyjádřit součtem mocnin základu dané soustavy vynásobeným příslušnými platnými číslicemi.

Nejčastější poziční soustavy

  • jedničková, r = 1 (počítání na prstech)
  • dvojková (binární) r = 2
  • osmičková (oktální/oktalová), r = 8
  • dekadická, r = 10
  • dvanáctková, r = 12 (již se nepoužívá, ale známe tucet a veletucet)
  • šestnáctková (hexadecimální), r= 16, pro čísla 10-15 se používají písmena A-F
  • šedesátková, r = 60 (měření času pro zlomky hodiny)

Každé číslo v poziční soustavě (kromě jedničkové) může mít celočíselnou část a zlomkovou část, oddělují se čárkou (anglosaské země oddělují tečkou).

Z-ADICKÁ SOUSTAVA: \(A_z = (a_n a_{n-1} ...a_1 a_0 , a{-1} a{-2} + ...a_{-m})_z; a_i, n, m \in N\)

  • \(a_i\) je z-adická číslice
  • z je báze soustavy
  • n je nejvyšší řád s nenulovou číslicí
  • m je nejnižší řád s nenulovou číslicí

Binární soustava

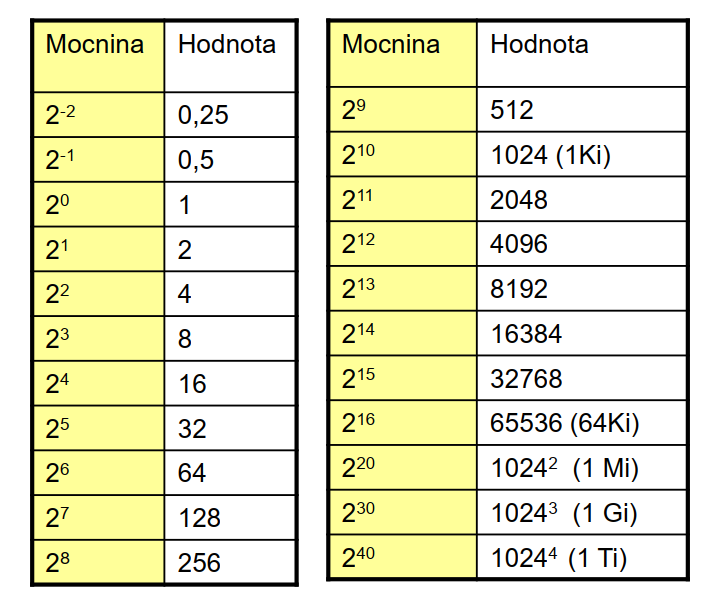
Zde se Z (báze) = 2.

Binární soustava
obr. 1: Binární soustava
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.
  • Ki (kibi)
  • Mi (mebi)
  • Gi (gibi)

Převody do jiné soustavy

Ukážeme si převod do dekadické soustavy. Máme dvě možnosti:

A) buď si převáděné číslo rozepíšeme na polynom a vyčíslíme v dané soustavě

\(A = 1001101_2\) \(A = 1 * 2^6 + 0 * 2^5 + 0 * 2^4 + 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77\)

B) použijeme tzv. modulo (%) - algoritmus zbytku po dělení

Převod z binární do dekadické soustavy
obr. 2: Převod z BIN soustavy do DEC soustavy
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.

Výsledný sloupec do binární soustavy zapisujeme odspoda nahoru.

Převod zlomkové části na intervalu <0, 1)

  • mějme číslo v desítkové soustavě 0,375
  • převádíme následovně:

\(0,375 * 2 = 0,75\)
\(0,75 * 2 = 1,5\)
\(0,5 * 2 = 1\)

Tedy, nalevo před desetinnou čárkou bude zákonitě 0. Poté napravo zapisujeme čísla z výsledků, která jsou PŘED danými desetinnými čárkami.

\(0,375_{10} = 0,011_2\)

Převod z Binární do Decimální soustavy

Buď provedeme binární dělení, tedy číslo zaspané v binární soustavě budeme dělit \(10\) zapsanými také v bináru, nebo si jednoduše rozepíšeme řadu v mocninách čísla 2 a sečteme.

Totéž uděláme pro zlomkové části (tedy za desetinnou čárkou). Zde je třeba si pamatovat, že první číslo za desetinnou čárkou/tečkou je \(2^{-1}\), protože poslední číslice z celého čísla je \(2^0\).

Příklady

\(1 0 1 1 0 1\) \(\Rightarrow\) \(1 * 2^5 + 0 * 2^4 + 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 32 + 8 + 4 + 1 = 45\)

\(1 1 0 0.1 0 1\) \(\Rightarrow\) \(2^3 + 2^2 . \frac{1}{2} + \frac{1}{8}\) \(\Rightarrow\) \(12.625\)

Sčítání, násobení a dělení čísel v binární soustavě

Sčítání v bináru
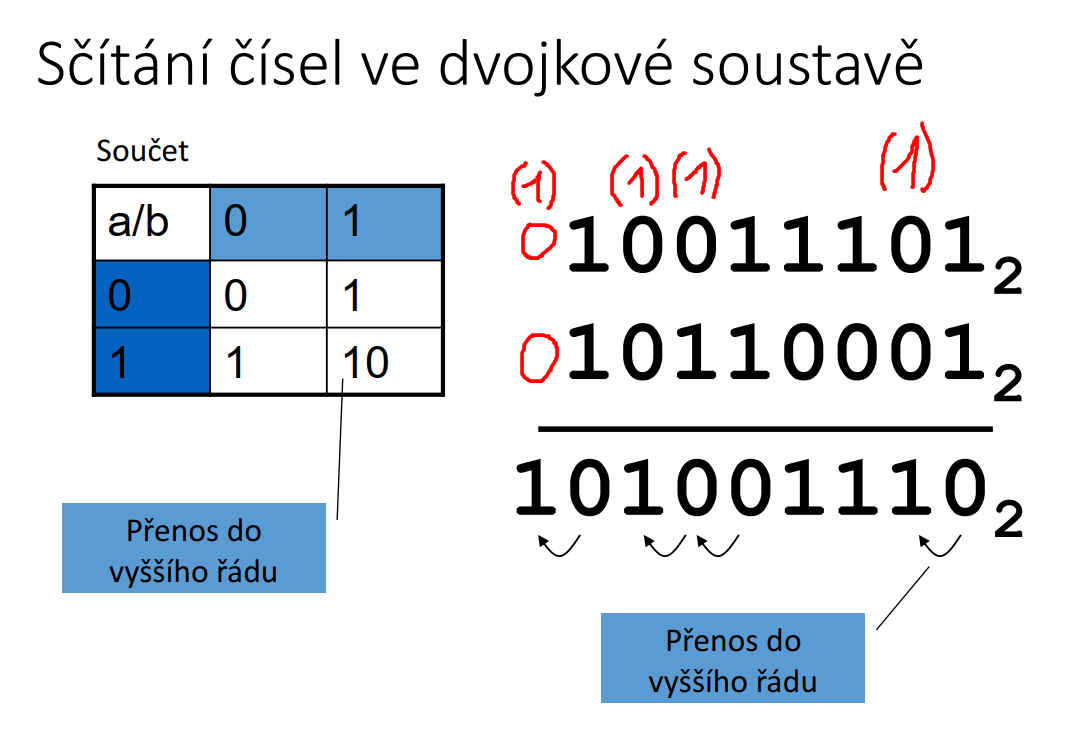
obr. 3: Sčítání v binární soustavě
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.

Sčítáme obdobně jako v dekadické soustavě, jen s tím rozdílem, že uplatňujeme pravidla následovně:

  • 0 + 1 = 1
  • 1 + 0 = 1
  • 0 + 0 = 0
  • 1 + 1 = 10
  • 1 + 1 + 1 = 11 (specifický případ, kdy sčítáme dvě jedničky nad sebou a schovali jsme si jedničku z předchozího řádu)

Dobře je to vysvětlené na tomto videu.

Násobení v bináru
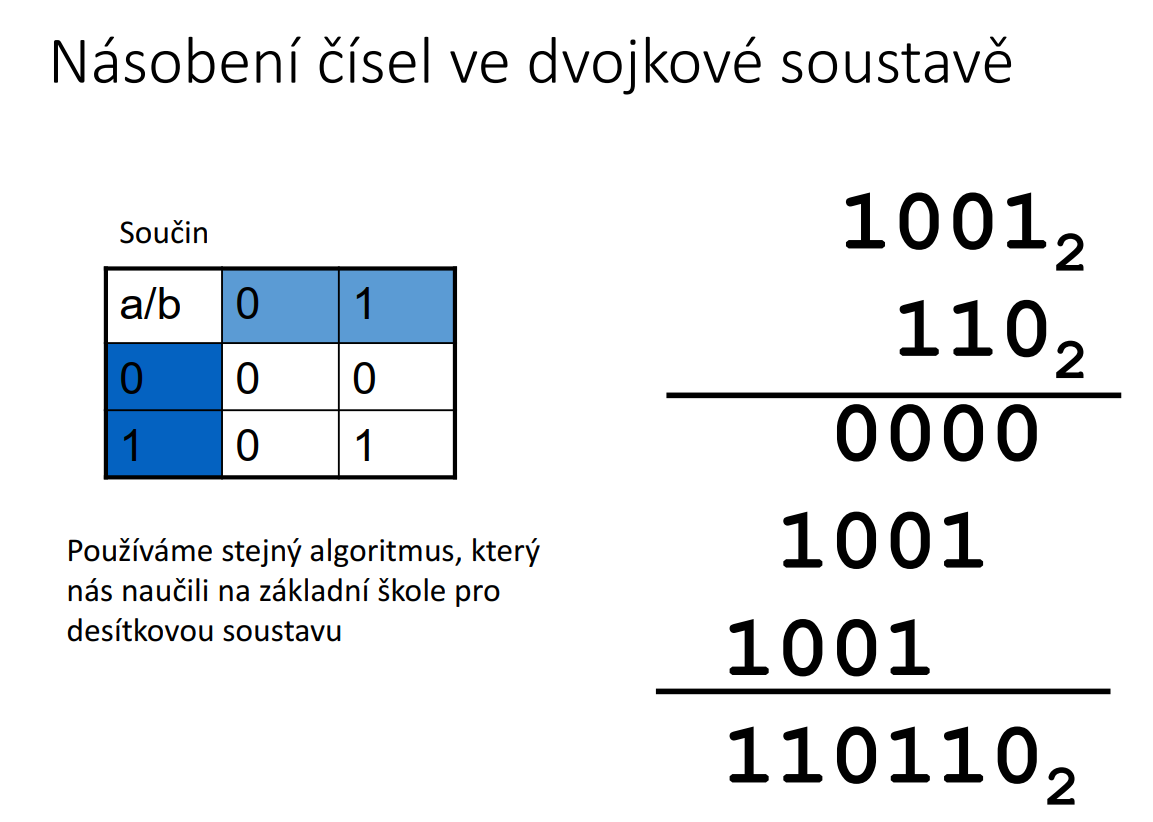
obr. 4: Násobení v binární soustavě
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.

Opět je to stejné, jako násobení v decimální soustavě, řídíme se pravidly dle tabulky z obrázku.

  • 0 * 0 = 0
  • 1 * 0 = 0
  • 0 * 1 = 0
  • 1 * 1 = 1
Dělení v bináru
obr. 5: Dělení v binární soustavě
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.

Dělení je o něco složitější, byť používáme stejnou metodu jako v desítkové soustavě. Postupujeme dělencem dokud nedojdeme k řádu, do nějž se vejde dělitel. Následně dělitel odečteme a k odečtu připisujeme další řády, dokud se nám tam dělitel opět nevejde.

Pokud se nám dělitel vejde do dělence, napíšeme 1, jinak 0.

Jiný příklad dělení:

Dělení v bináru
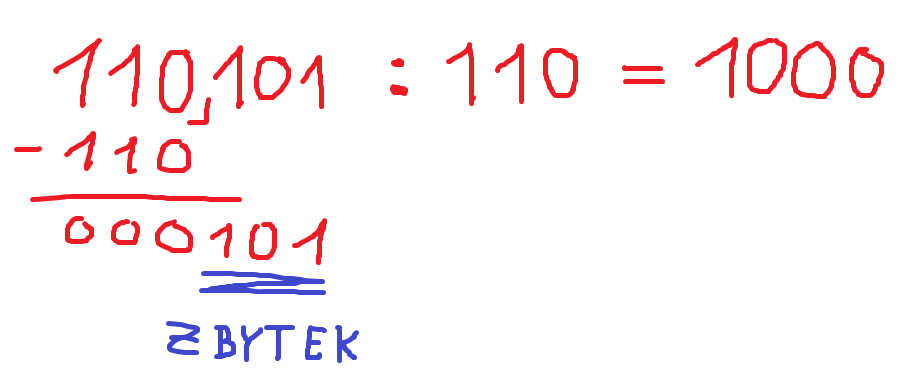obr. 6: Dělení v binární soustavě
zdroj: TRTÍLEK, Ondřej. Vlastní zpracování. České Budějovice, 2023.

Za každý přidaný řád (modře podtržený) dopisujeme do výsledku 0, dokud nedojdeme na konec dělence. Poté vyhodnotíme, zda se tam dělitel vejde či nikoli. pokud nikoli, tak jej považujeme za zbytek.

Vždy si můžeme převést čísla do decimální soustavy a zkontrolovat. 
Zde je to 53 : 6. Toto vyjde 8 se zbytkem 5.

Hexadecimální soustava

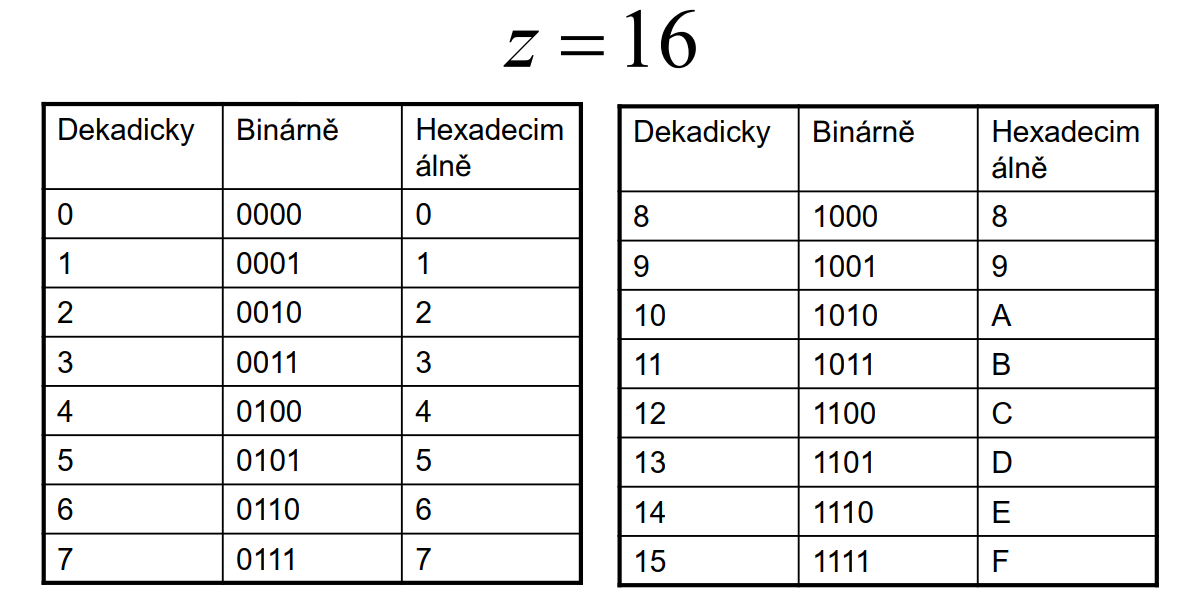
Hexadecimální soustava
obr. 7: Hexadecimální soustava
zdroj: SKRBEK, Miroslav. Architektura počítačů I: UAI/698 Přednášky. Ver 1.0.9. Ústav aplikované informatiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích, 2019. PDF přednáška.

Příklady v hexadecimální soustavě

\(78FF\) \(\Rightarrow\) \(15 * 16^0 + 15 * 16^1 + 8 * 16^2 + 7 * 16^3\) \(\Rightarrow\) \(15 + 240 + 8 * 256 + 7 * 4096\) \(\Rightarrow\) \(255 + 2048 + 28672\) \(\Rightarrow\) \(30 975_{10}\)

\(A5\) \(\Rightarrow\) \(5 * 16^0 + 10 * 16^1\) \(\Rightarrow\) \(165_{10}\)

Příbuzné soustavy a převody

Příbuzné soustavy jsou takové soustavy, kde základ jedné soustavy je mocninou základu druhé soustavy.

Binární, čtyřková, oktální, hexadecimální.

Decimální, stovková, tisícová soustava.

Tedy, budu-li převádět z hexadecimální do binární, rozepíšu jednotlivé znaky do 4 bitů. Budu-li převádět z binární do hexadecimální, tak si bity rozdělím právě po 4.

Začínám vždy zprava, abych mohl případně poslední čtveřici doplnit o 0.

\(AC35\) \(\Rightarrow\) \(1010 | 1100 | 0011 | 0101\) \(1001110011011\) \(\Rightarrow\) \(0001 | 0011 | 1001 | 1011\) \(\Rightarrow\) \(139B\)

U čtyřkové soustavy vytvářím dvojice a u osmičkové soustavy trojice (při převodu do bináru zapisujeme daná čísla 3 respektive 2 bity).

\(750_8\) \(\Rightarrow\) \(111 | 101 | 000_2\)
\(2131_4\) \(\Rightarrow\) \(10 | 01 | 11 | 01_2\)

\(100111101_2\) \(\Rightarrow\) \(100 | 111 | 101\) \(\Rightarrow\) \(475_8\)
\(1110101_2\) \(\Rightarrow\) \(01 | 11 | 01 | 01\) \(\Rightarrow\) \(1311_4\)

Kódování znaků

Znak kódu je znak abecedy zapsaný v binární podobě, přičemž se pro zápis používají stanovená pravidla/standardy: ASCII, UTF-8, UTF-16, UTF-32 nebo Windows-1250 (pro kódování češtin na systémech Windows). Znakových sad je však mnoho.

ASCII

Nejzákladnější znakovou sadou je tzv. ASCII tabulka (American Standard Code for Information Interchange). Původní tabulka obsahuje 128 platných znaků kódovaných pomocí 7 bitů v rozsahu (0-127). Nezohledňuje diakritiku.

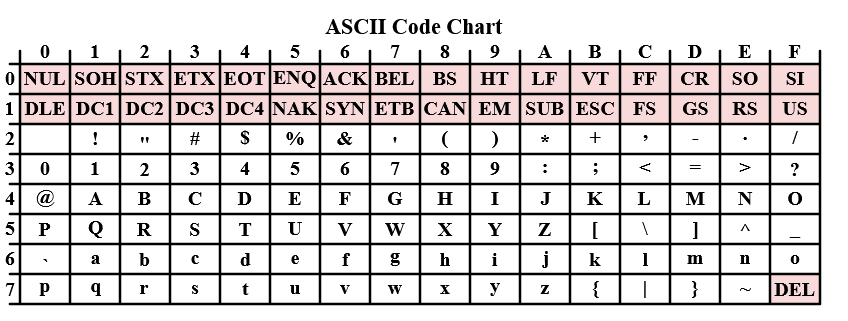
Tabulka obsahuje jednotlivé znaky, jejich číselnou hodnotu v decimální soustavě a v hexadecimální. Případně jen v hexadecimální (viz obrázek níže).

ASCII tabulka
obr. 8: ASCII tabulka
zdroj: ASCII. In: Wikipedie Otevřená Encyklopedie [online]. 2008 [cit. 2023-05-11]. Dostupné z: https://upload.wikimedia.org/wikipedia/commons/4/4f/ASCII_Code_Chart.svg.

Nejprve označíme řádek, poté sloupec, tím dostaneme hexadecimální kód znaku a posléze jej převedeme na binární.

  • \(k\) - \(6B_{16}\) - \(01101011_2\)
  • \((\) - \(28_16\) - \(00101000_2\)

Každý znak má vlastní bitovou reprezentaci tvaru, tomuto se říká FONT. Font zobrazuje v grafické podobě znak/symbol.

UTF (Unicode)

Jednotlivé standardy UTF nám říkají kolika bity se jednotlivé znaky kódují. Jestli 8, 16 nebo 32 bity.

  • znak \(B\)
  • \(0x42\) - UFT-8
  • \(0x0042\) - UFT-16
  • \(0x00000042\) - UFT-32

Reprezentace čísel se znaménkem a floating

Řádová mřížka Popisuje formát zobrazených čísel v počítači. Používá se z důvodu omezení při zobrazení čísel na menší rozsah (např. 1 bytu). Šířky řádových mřížek mohou být 8, 16, 32 či 64 bitů.

V závislosti na umístění řádové čárky určujeme rozsah zobrazitelných řádů čísla:

  • \(n\) nejvyšší (MSB - Most Significant Bit)
  • \(m\) nejnižší (LSB - Least Significant Bit)
Řádová mřížka
obr. 9: Binární řádová mřížka zachycující hodnotu 001011,01
zdroj: HALUZA, Pavel, Jiří RYBIČKA a Tomáš HÁLA. Úvod do informatiky [online]. Brno: KONVOJ, spol. s.r.o, 2018 [cit. 2023-05-11]. ISBN 978-80-7302-174-0. Dostupné z: https://www.konvoj.cz/Nakladatelstvi/Knihy/100289-haluza-rybicka-hala-scriptum-43-uvod-do-informatiky/100289-uvod-do-informatiky.pdf

Vlastnosti mřížky

  1. délka mřížky - vyjadřuje počet rozlišitelných hodnot (řádů), značíme \(l\)
  2. jednotka - představuje nejmenší kladné zobrazitelné číslo, značíme \(\varepsilon\)
  3. modul - představuje nejmenší číslo, které již zobrazitelné NENI, značíme \(M\) nebo \(Z\)
  4. pozice řádové čárky (může být plovoucí či pevná)

Operační paměť počítače rozdělujeme na adresovatelné jednotky o velikosti 1 Byte (slabiky). Délka řádové mřížky je proto vždy celým násobkem slabik.

Pro řádovou mřížku platí dále následující obecná pravidla:

  • \(l = m + n + 1\)
  • \(\varepsilon = z^{-m}\), je to číslo, které má jedničku pouze v nejnižším řádu
  • \(Z = 2^{n+1}\), jedná se o číslo, které má jedničku v řádu, který již není v mřížce obsažen

Overflow a Underflow

Overflow - přetečení Je-li délka řádové mřížky menší, než počet řádů čísla, které chceme do mřížky vložit, nebude toto číslo v mřížce zobrazitelné. Uloží se jen ty řády, které se do mřížky vejdou, zbytek řádů bude ignorován.

Při přetečení dojde ke ztrátě přesnosti čísla. Nevadí to tolik u ignorovaných nízkých řádů, ale ztráta nejvyšších řádů čísla znamená úplné znehodnocení číselného údaje.

K přetečení může dojít zejména při sčítání operandů se stejnými znaménky (odečítání s různými znaménky).

Underflow - podtečení Číslo je pro řádovou mřížku velmi malé, blíží se nule (je daleko za řádovou čárkou). Do řádové mřížky jej posléze zapíšeme jako 0, čímž dojde k zaokrouhlení a zkreslení.

Reprezentace záporných čísel

Problémem reprezentace čísel v počítači je binární zápis znaménka. Existují tří způsoby kódování pro práci se znaménkem:

  1. Přímý kód
  2. Aditivní kódování
  3. Doplňkové kódování

Přímý kód - sign magnitude

Forma zápisu je pro člověka čitelná. Nicméně HW pro zpracování takového kódu by byl zbytečně pomalý a složitý.

  • znaménko je reprezentováno tzv. znaménkovým bitem (nejvyšším řádem mřížky)
  • nabývá 0 je-li číslo kladné a 1 je-li číslo záporné (nahrazuje znaménko -)
Přímý kód
obr. 10: Reprezentace 4 bitových čísel se znaménkem v přímém kódu
zdroj: HALUZA, Pavel, Jiří RYBIČKA a Tomáš HÁLA. Úvod do informatiky [online]. Brno: KONVOJ, spol. s.r.o, 2018 [cit. 2023-05-11]. ISBN 978-80-7302-174-0. Dostupné z: https://www.konvoj.cz/Nakladatelstvi/Knihy/100289-haluza-rybicka-hala-scriptum-43-uvod-do-informatiky/100289-uvod-do-informatiky.pdf
  • kladná čísla rostou zleva
  • záporná rostou zprava
  • dvojí vyjádření 0, rovněž platí \(-0 > 0\)
  • původní n bity pro vyjádření čísla jsou sníženy na \(n -1\), protože jeden bit je na znaménko
  • zobrazíme tedy \(2^{n -1}\) hodnot
  • každé zobrazené číslo, ale nemusí mít znaménko
  • umíme zde zobrazit rozsah \(-2^{n-1} + 1\) až \(2^{n-1} - 1\)

Příklad Vyjádření čísla -53 na 8 bitech se znaménkem:

  1. převedeme do bináru \(110101\)
  2. doplníme zleva nulami do celé délky mřížky \(00110101)
  3. upravíme znaménkový bit
  4. posloupnost je: \(10110101\)

Inverzní kód - one's complement (jedničkový doplněk)

  • používáme pro hledání reprezentace čísla v binárním doplňkovém kódu
  • kladná čísla jsou beze změny
  • záporná čísla mají svůj doplněk do jedničky
  • doplněk 0 je jednička
  • doplněk 1 je nula
  • provádíme inverzi všech bitů čísla
Inverzní kód
obr. 11: Reprezentace 4 bitových čísel se znaménkem v inverzním kódu
zdroj: HALUZA, Pavel, Jiří RYBIČKA a Tomáš HÁLA. Úvod do informatiky [online]. Brno: KONVOJ, spol. s.r.o, 2018 [cit. 2023-05-11]. ISBN 978-80-7302-174-0. Dostupné z: https://www.konvoj.cz/Nakladatelstvi/Knihy/100289-haluza-rybicka-hala-scriptum-43-uvod-do-informatiky/100289-uvod-do-informatiky.pdf
  • zachováváme relaci mezi kladnými a zápornými
  • oboje roste zleva doprava
  • reprezentace i zobrazovaný rozsah je stejná jako v přímém kódu

Příklad Vyjádření čísla -53 na 8 bitech v inverzním kódu:

  1. převedeme do bináru \(110101\)
  2. doplníme zleva nulami do celé délky mřížky \(00110101)
  3. provedeme inverzi všech bitů
  4. posloupnost je: \(11001010\)

Doplňkový kód - two's complement (dvojkový doplněk)

  • odstraňuje dvojí reprezentaci 0
  • tvoří se stejně jako inverzní kód
  • záporné číslo je reprezentováno přičtením jedničky
  • nejpoužívanější číselný kód pro celá čísla a pro většinu operací na moderních strojích
Doplňkový kód
obr. 11: Reprezentace 4 bitových čísel se znaménkem v doplňkovém kódu
zdroj: HALUZA, Pavel, Jiří RYBIČKA a Tomáš HÁLA. Úvod do informatiky [online]. Brno: KONVOJ, spol. s.r.o, 2018 [cit. 2023-05-11]. ISBN 978-80-7302-174-0. Dostupné z: https://www.konvoj.cz/Nakladatelstvi/Knihy/100289-haluza-rybicka-hala-scriptum-43-uvod-do-informatiky/100289-uvod-do-informatiky.pdf

Příklad Vyjádření čísla -53 na 8 bitech v doplňkovém kódu:

  1. převedeme do bináru \(110101\)
  2. doplníme zleva nulami do celé délky mřížky \(00110101)
  3. provedeme inverzi všech bitů
  4. posloupnost je: \(11001010\)
  5. K výsledku přičteme jedničku
  6. Výsledek: \(11001011\)

  • lze to vyjádřit také tak, že si vypočítáme maximální hodnotu na 8 bitech \(2^8\)

  • od této hodnoty odečteme (resp. přičteme k ní) číslo -53

  • výsledek je 203

  • převedeme jej do bináru

  • binární hodnota tohoto čísla odpovídá právě číslu -53

  • nemůže dojít k záměně, protože zobrazujeme pouze hodnoty od -127 do 128

  • interval zobrazitelných hodnot je \(-2^{n-1}\) až \(2^{n-1} - 1\)

Aditivní kód (biased)

  • 0 posunujeme přibližně do poloviny intervalu
  • ke každému číslu přičteme konstantu
  • interval zobrazených čísel je \(-2^{n-1}\) až \(2^{n-1} - 1\)
Aditivní kód
obr. 11: Reprezentace 4 bitových čísel se znaménkem v aditivním kódu
zdroj: HALUZA, Pavel, Jiří RYBIČKA a Tomáš HÁLA. Úvod do informatiky [online]. Brno: KONVOJ, spol. s.r.o, 2018 [cit. 2023-05-11]. ISBN 978-80-7302-174-0. Dostupné z: https://www.konvoj.cz/Nakladatelstvi/Knihy/100289-haluza-rybicka-hala-scriptum-43-uvod-do-informatiky/100289-uvod-do-informatiky.pdf
  • kladná čísla mají v MSB jedničku
  • záporná mají v MSB nulu

BCD - binary coded decimal

  • používá se v kalkulačkách, měřících přístrojích
  • princip je uložení čísel desítkové soustavy do půlslabiky (4 bity)
  • jiné číslice se nevyskytují
  • zhuštěný tvar BCD - v jedné slabice jsou dvě čísla
  • nezhuštěný tvar BCD - v jedné slabice je jedno číslo
  • znaménko \(+\) je často zachyceno jako 1010
  • znaménko \(-\) jako 1011
  • znaménko tedy zabírá stejný počet bitů jako číslice

Příklad Vyjádření čísla 38 v BCD:

  1. 3 do bináru \(0011\)
  2. 8 do bináru \(1000\)
  3. nezhuštěný tvar na 2 bajtech: 00000011 00001000
  4. zhuštěný tvar na 1 bajtu: \(00111000\)

Floating - racionální čísla s plovoucí čárkou

  • tento zápis standardizuje norma IEEE 754
  • jedná se o tzv. semilogaritmický tvar, jinak též vědecká notace (viz zde)

POJMY

  • mantisa - upravuje číslo do tvaru, ve kterém je čárka umístěna za první nenulovou číslici, přičemž platí \(1 \leq m < z\)
  • m je mantisa, z je základ soustavy
  • exponent - vyjadřuje počet řádů, o které bylo nutné čárku posunout
  • kladný exponent (posun doleva), záporný (posun doprava)
  • každé racionální číslo pak lze vyjádřit součinem mantisy a základu soustavy umocněného exponentem
  • 0,00004945 \(\Rightarrow\) \(4,945 * 10^{-5}\)

Paměťový prostor pro vyjádření racionálních čísel s floatingem je rozdělen na 3 části: znamenko, mantisa a exponent.

Exponent se vyjádří v aditivním kódu s posunem o \(2^{n-1} - 1\). Mantisa by vždy začínala jedničkou (v bináru je každá nenulová číslice jednička). Tato jedničma se neukládá, jde o tzv. skrytý bit. Ušetřené místo slouží k zobrazení dalšího bitu zlomkové části - zvyšuje se přesnost zobrazení čísla.

3 formáty zobrazení racionálních čísel s floatingem

  1. single precision (jednoduchá přesnost): 32 bitů celkem. 1 bit pro znaménko, 8 bitů exponent, zbytek je mantisa (23 bitů)
  2. double precision (dvojitá přesnost): 64 bitů celkem, 1 bit znaménko, 11 bitů pro exponent a zbytek pro mantisu (52 bitů)
  3. extended precision (rozšířená přesnost): 80 bitů celkem, 1 bit znaméneko, 15 bitů exponent, zbytek je mantisa (64 bitů)

Algoritmus převodu

  1. Absolutní hodnotu čísla převedeme do bináru
  2. Normalizujeme výsledek (mantisu zachytíme binárně), expnent decimálně
  3. Exponent převedeme do aditivního kódu posunem o konstantu
  4. Zkrátíme mantisu na požadovanou přesnost (řešíme pouze bity za řádovou čárkou)
  5. Nastavíme hodnotu znaménkového bitu

Příklad

  • máme číslo 64.2 - single precision
  • převedeme do bináru
  • \(64 \Rightarrow 1000000\)
  • \(0.2 \Rightarrow 0.001100110011...\)
  • \(1000000.001100110011...\)
  • výsledek normalizujeme na: \(1.000000001100110011... * 2^6\)
  • upravíme exponent přičtením konstanty 127 (\(2^{8-1} - 1)\), exponent je 8 bitový, tedy n by mělo být 8 (?)
  • získáme tím číslo 133 (6 + 127)
  • převedeme do binárního kódu (10000101)
  • vezmeme část mantisi (za řádovou čárkou) a zkrátíme na požadovaných 23 bitů
  • dostaneme posloupnost 00000000110011001100110
  • nastavíme znaménkový bit na 0 (máme kladný exponent)
  • složíme dohromady
  • VÝSLEDEK: |0|10000101|00000000110011001100110|

ZDROJE