Učení bez učitele
Samoorganizující se neuronové sítě (SOM - Self-Organizing Map)
Tato NS byla poprvé popsána v roce 1982 finským vědcem Teuvo Kohonenem, proto se jí rovněž říká Kohonenova síť. Jedná se o základní princip soutěžního učení, tj. učení bez učitele.
Jedná se o dvouvrstvou síť s úplným propojením neuronů mezi vrstvami (více viz Struktura).
Princip
Vytvoření množiny reprezentantů mající stejné pravděpodobnosti výběru - vybereme-li náhodný input vektor z rozdělení pravděpodobnosti odpovídající rozdělení tréninkové množiny, bude mít každý takový reprezentant přiřazenu takovou pravděpodobnost, která je mu nejblíže.
De facto provádíme shlukovou analýzu, ale nemusíme znát dopředu počet shluků (u K-MEANS je znát musíme).
Váhy se adaptují na základě statistických vlastností trénovací množiny: jsou-li si dva vzory na vstupu blízké, způsobí odezvu na fyzicky si blízkých neuronech, ve výstupní množině.
Cílem je zobrazit mnohodimenzionální data v mnohem jednodušším prostoru.
Struktura sítě
- Lineární uspořádání (řetízek) - (vzdálenost mezi neurony je 1)
- Čtvercová mřížka (vzdálenost rovnoběžně 1, diagonálně 2 Manhattanská vzdálenost, nebo \(\sqrt{2}\) eukleidovská)
- Hexagonální mřížka (vzdálenost mezi neurony je 1 ve všech směrech)
- Toroid mřížka (vzdálenost rovnoběžně 1, diagonálně 2 Manhattanská vzdálenost, nebo \(\sqrt{2}\) eukleidovská)
| obr. 1: Jednotlivé topologie SOM |
| zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška. |
Nejčastějším typem topologie SOM je Lineární a nebo dvojrozměrná mřížka. Topologie určuje, které neurony spolu sousedí - toto je důležité pro adaptační proces.
Proces učení
\[y_i = \sum_{j=1}^{N} (x_j - w_{ij})^2\]
Vybavování
Předložíme vzor na vstup/vstupní vrstvu a vypočteme odezvy. Neuron s nejmenší odezvou (reprezentant) je vítězný neuron a reprezentuje shluk, kam vzor patří.
Učení
Vezmeme vítěze a jeho váhy posuneme o kousek blíže k učenému vektoru. Kromě vítěze upravujeme váhy i sousedních neuronů - čím dále tím méně upravujeme. Postup opakujeme do \(\alpha (t)\) = 0.
\[\Delta w_{ij} = \alpha (t) (x_j - w_{ij}) (h(i, b))\]
- \(\alpha (t)\): rychlost učení, proměnná v čase, jež klesá do nuly
- funkce \(h(i, b)\) je maximální, pokud i je indexem vítězného neuronu \((i = b)\), pokud je to jiný neuron, tak funkce h klesá v závislosti na vzdálenosti od vítězného neuronu.
Extrémní je hodnota 1 pro \((b = i)\), jinak 0.
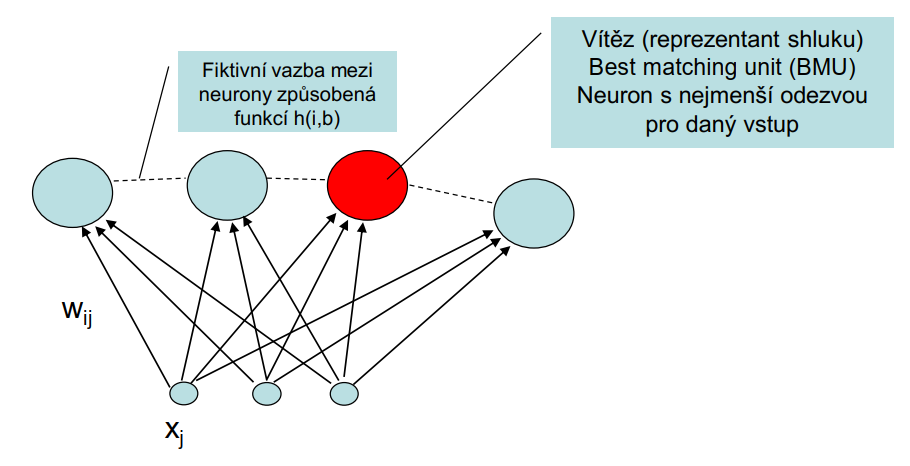 |
|---|
| obr. 2: Popis struktury SOM |
| zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška. |
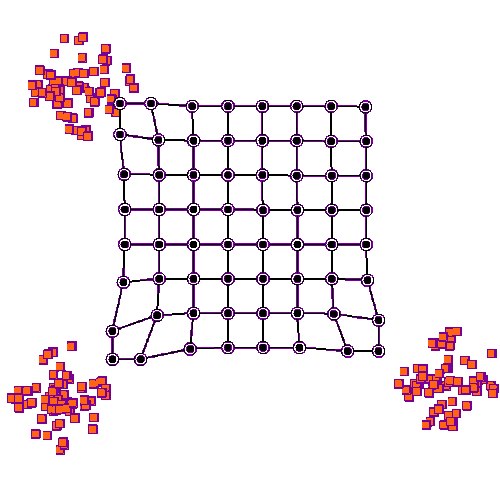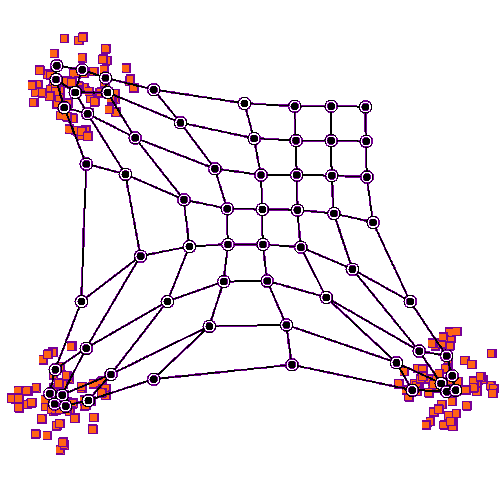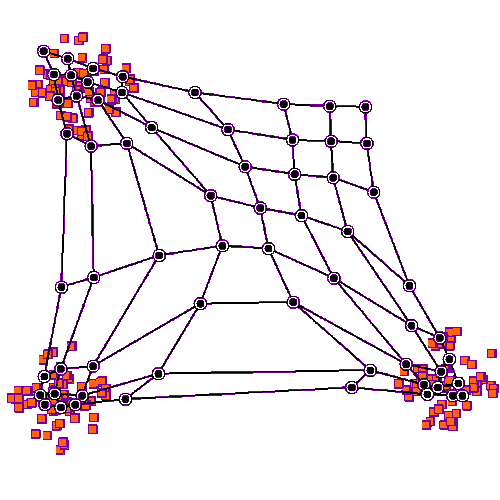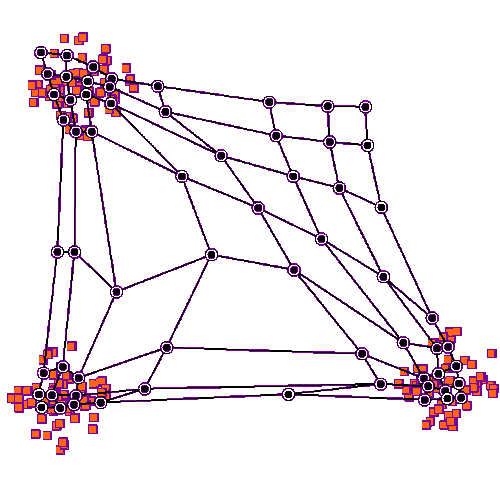 |
|---|
| obr. 3: Vizualizace shlukování v rámci SOM |
| zdroj: Trénování samoorganizující sítě. In: , Chompinha. Wikipedie Otevřená Encyklopedie [online]. Wikimedia Commons, 2019 [cit. 2023-05-09]. Dostupné z: https://cs.wikipedia.org/wiki/Samoorganizuj%C3%ADc%C3%AD_s%C3%AD%C5%A5#/media/Soubor:TrainSOM.gif |
Funkce \(h (i, b)\)
Tato funkce nám určuje, jak se budou měnit váhy neuronů blízkých vítěznému neuronu \(\Rightarrow\) Jak se budou prototypy reprezentované neurony posouvat směrem k učenému vzoru. Nejvíce bude přitahován vítězný neuron a nejméně neuron, který je od vítězného nejdále.
Pokud je funkce \(h (i, b)\) záporná, tak jsou neurony odpuzovány, je-li kladná, jsou přitahovány, takto se tvoří shluky.
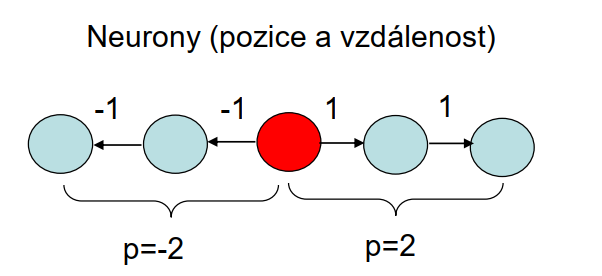 |
|---|
| obr. 4: Vzdálenost a neurony |
| zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška. |
Při učení se začíná s plochou \(h (i, b)\), která postupně nabývá strmější charakter "Mexický klobouk, viz obrázek níže.
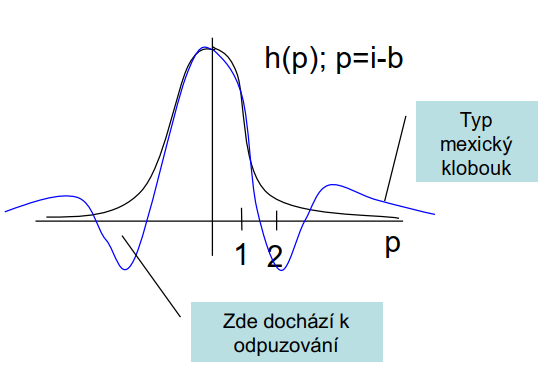 |
|---|
| obr. 5: Průběh funkce h (i, b) |
| zdroj: SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška. |
Jinými slovy, vítězný neuron a jeho nejbližší sousedé budou měnit váhový vektor o poměrnou vzdálenost směrem k aktuálnímu vstupu. Cílem je, aby vítězný neuron, který se nejvíce podobá vstupnímu vektoru/vzoru ještě více zlepšil svoji relativní pozici vůči tomuto vstupu. Problémem v průběhu adaptace může být nevhodná náhodná inicializace počátečních vah. Toto vede následně ke změnám směrem k počátečním neuronům ve výstupní vrstvě a tedy pouze jeden z těchto neuronů vyhraje kompetici (soutěž) a zbytek neuronů je nevyužit.
V aktivním režimu to funguje tak, že nejbližší neuron vstupnímu vzoru je excitován na hodnotu 1 a zbylé neurony na hodnotu 0. Excitovaný neuron je navíc schopen rozpoznat celou třídy podobných vzorů/vektorů. Tento princip Vítěz bere vše je realizován tzv. Laterální inhibicí - tj. všechny výstupní neurony jsou propojeny laterálními vazbami přenášejícími inhibiční signály.
Každý neuron se následně snaží oslabit ty sousední, a to silou úměrnou jeho potenciálu (blíže vstupu se potenciál zvyšuje).
Výsledek je, že výstupní neuron s největším potenciálem utlumí všechny ostatní neurony a sám zůstane aktivní.
Algoritmus SOM
- Inicializujeme váhy neuronů náhodnými hodnotami a nastavíme počáteční hodnotu koeficientu α(t).
- Vybereme vektor z učící množiny a přiložíme na vstup sítě.
- Vypočteme výstupy neuronů \(y_i\).
- Zjistíme neuron s nejmenší odezvou - reprezentant.
- Pro každý neuron upravíme váhu o \(\Delta {w_ij}\).
- Dokud nevyčerpáme učící množinu, pokračujeme bodem 2.
- Snížíme koeficient \(\alpha (t)\), dokud je \(\alpha (t) > 0\), tak pokračujeme bodem 2, od počátku učící množiny.
U-Matice
Zachycuje odezvu SOM. Barva neuronů v hexagonální mřížce nám indikuje průměrnou vzdálenost vah daného neuronu od jeho sousedů. Na obrázku níže jsou bíle zachyceny neurony s podobnými vahami - tvoří shluky - zatímco tmavá políčka nám shluky oddělují (neurony mají zcela jiné váhy).
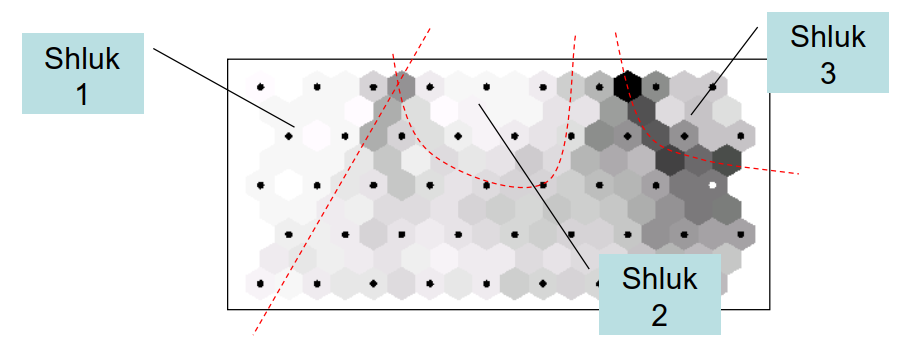 |
|---|
| obr. 6: U-Matice |
| zdroj: HOLLMEN, Jaakko. U-matrix representation of the Self-Organizing Map. In: Jaakko Hollmén's Research Home Page [online]. Aalto University School of Science: Jaakko Hollmén, 1996 [cit. 2023-05-09]. Dostupné z: http://users.ics.aalto.fi/jhollmen/dippa/node24.html |
ZDROJE
- SKRBEK, Miroslav. Výpočetní inteligence: Úvod do předmětu. LS2019/2020. Praha, 2020, 107 s. PDF přednáška.
- VOLNÁ, Eva. EVOLUČNÍ ALGORITMY A NEURONOVÉ SÍTĚ: URČENO PRO VZDĚLÁVÁNÍ V AKREDITOVANÝCH STUDIJNÍCH PROGRAMECH. Ostravská univerzita v Ostravě, 2012, 152 s. Dostupné také z: http://physics.ujep.cz/~mmaly/vyuka/MPVT_II/Heuristiky/SOMAdetail-Evolucni_algoritmy_a_neuronove_site+Genetika.pdf