Binární vyhledávací stromy

definice, užití a implementace, vyvažování, AVL stromy – princip algoritmu

Definice

Binární vyhledávací strom je datová struktura založená na binárním stromu, v němž jsou jednotlivé prvky uspořádány tak, aby v tomto stromu bylo možné rychle vyhledávat.

Binární strom

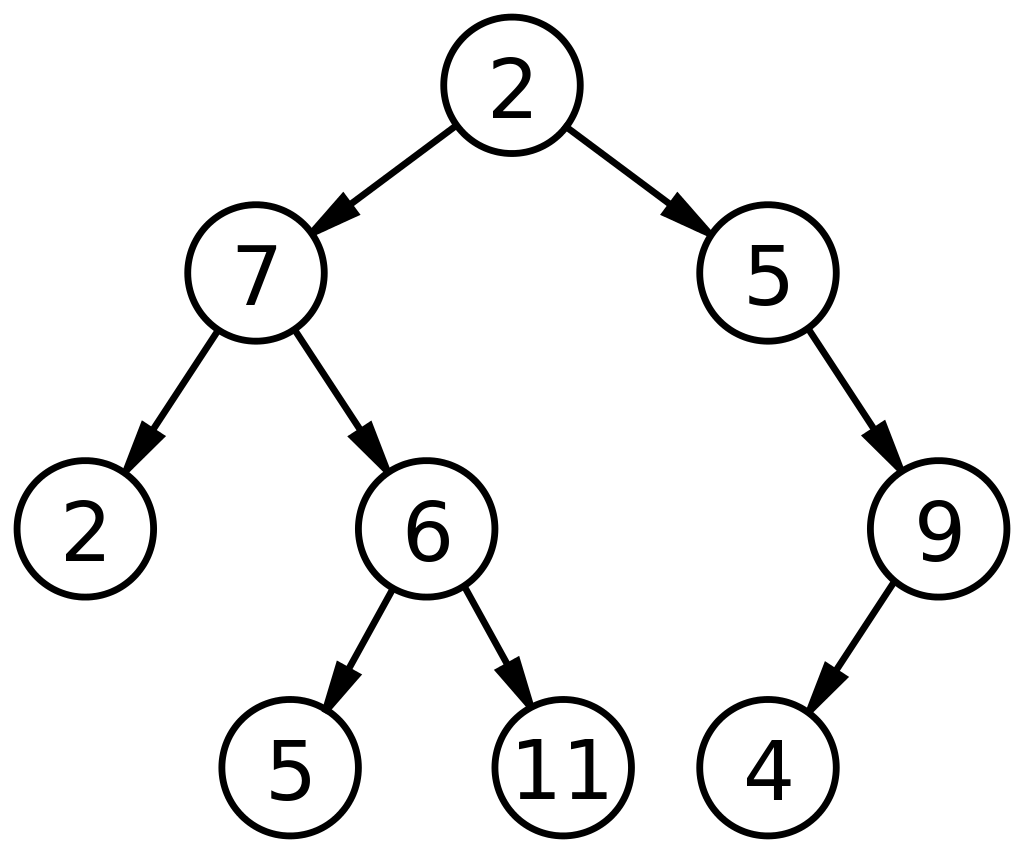
Jedná se o orientovaný graf s jedním vrcholem (kořen stromu), z něhož vede cesta ke všem ostatním vrcholům. Každý vrchol může mít maximálně dva potomky. Každý potomek může mít maximálně jednoho předka (s vyjimkou kořene, ten nemá žádného předka).

Binární strom
obr. 1: Binární strom
Převzato z: https://cs.wikipedia.org/wiki/Bin%C3%A1rn%C3%AD_strom

Implementace a vlastnosti vyhledávacích binárních stromů

  • jedná se o binární strom (každý uzel má nejvýše dva potomky)
  • každému uzlu je přiřazen určitý klíč (hodnota)
  • levý podstrom každého uzlu obsahuje pouze menší hodnoty než je klíč tohoto uzlu
  • pravý podstrom každého uzlu obsahuje pouze větší hodnoty než je klíč tohoto uzlu

Užití

  • konstrukce a prohledávání asociativních polí (klíč - hodnota)
    • průchod je pomalejší nežli hashovací tabulka, ale průchod stromem vydá seznam seřazených hodnot (hodí se na intervalové dotazy)
  • slouží jako základ pro komplexnější vyhledávací datové struktury

Operace

Máme základní čtyři:

  • vyhledávání
  • vkládání
  • mazání
  • procházení stromu

Vyhledávání

Probíhá rekurzivně. Začínáme v kořenu stromu. Algoritmus porovná hledanou hodnotu s klíčem uzlu. Pokud se rovná, našli jsme hledanou hodnotu. Pokud je menší, jdeme doleva, pokud je větší, jdeme doprava. Toto se děje, dokud jsme nenalezli hodnotu, nebo nedorazili do listu stromu.

Časová složitost vyhledávání závisí na hloubce stromu. V průměrném případě má logaritmickou časovou složitost O(log n), ale pokud je strom nevyvážený a podobá se seznamu, může mít i lineární časovou složitost O(n). Otázka správného vyvážení je z tohoto pohledu kritická a řeší ji například AVL-strom.

Vkládání

Probíhá podobně jako vyhledávání, akorát hledanou hodnotou je hodnota vkládaného uzlu. Mohou nastat dva případy:

  • strom již hodnotu obsahuje, není třeba ji vložit
  • algoritmus narazil na neexistující uzel (například chce jít z uzlu doprava, ale žádný uzel tam není) -> našli jsme místo, kam uzel patří

Mazání

Zde může nastat několik případů:

  • hledaným uzlem je list, ten můžeme klidně smazat
  • hledaným uzlem je uzel s jedním potomkem -> smažeme uzel a nahradíme tento uzel potomkem
  • hledaný uzlem je uzel se dvěma potomky -> hodnota uzlu je nahrazena nejbližší vyšší (nejlevější uzel pravého podstromu), nebo nižší hodnotou (nejpravější uzel levého podstromu)

Procházení stromu

Pouze procházíme strom, nijak ho neměníme, složitost odpovídá výšce stromu.

Řazení uzlů

Jedná se o proces zařazení hodnot stromu dle velikosti.

Vkládáme všechny hodnoty které chceme seřadit do vhodně uspořádané datové struktury -> binární strom. Následně stromem projdeme do hloubky a získáme seznam hodnot uspořádaný podle velikosti.

  • nejhorší případ je n2 času, a to pokud se přidávají již seřazené hodnoty. Ty se totiž spojí do seznamu takže strom nemá levé větve.

Metody vkládání a mazání jsou často destruktivní -> tedy ničí vyváženost našeho stromu (to je takový strom, kde je rozdíl výšky podstromů uzlu menší než 2).

Jak vyvážíme strom?

AVL stromy

Jedná se o typ binárního vyhledávacího stromu. Konkrétně se jedná o samovyvažující se binární vyhledávací strom.

K vlastnostem binárních vyhledávacích stromů přidává AVL další vlastnost:

  • délka nejdelší větve levého a pravého podstromu každého uzlu se liší nejvýše o 1, jinak strom není vyvážený

AVL strom definuje postupy zajišťující vyvážení stromu pro operace, jež mají šanci strom zdegenerovat:

  • vkládání
  • mazání

Vše je založeno na kritériu vyváženosti. Jedná se o číslo, které nám říká, jak se liší výška levého a pravého podstromu daného uzlu. Každý uzel má ideálně svoje kritérium vyváženosti, které pravidelně aktualizujeme.

Vkládání do AVL stromu

Stejné jako u binárního vyhledávacího stromu, až na to, že po vložení se aktualizují koeficienty vyváženosti uzlů, které byly na cestě směrem ke kořenu.

Není-li splněno kritérium vyváženosti, musíme provést vyvažování stromu pomocí cyklické záměny ukazatelů (rotace stromu).

  • Při vkládání stačí vyvážit pouze první nalezený uzel, jehož koeficient vyváženosti je porušen, tím že ho opravíme, vyvážíme celý strom -> změna vyvolaná přidáním uzlu ovlivní pouze první nevyvážený uzel a jeho podstromy.

Mazání z AVL stromu

Stejné jako u binárního vyhledávacího stromu tím, že pokud dojde k porušení vyváženosti, provede se vyvážení. Na rozdíl od vyvažování při vkládání uzlů, při odebírání uzlů se musí projít celá cesta až do kořene stromu a opravit koeficienty vyvážení a případně provést rotace -> změna vyvolaná odstraněním může ovlivnit vyváženost celého podstromu kořene.

Vyvažování

Vyvážení docílíme tím, že vhodně zrotujeme celý podstrom, tak aby byla splněna vlastnost AVL stromů (Výška dvou podstromů se může lišit maximálně o 1)

  • rotací změníme pořadí uzlů ve stromu; máme dva druhy rotace:

    • jednoduchá (rotujeme doleva, pokud je pravý podstrom vyšší; rotujeme doprava pokud je levý podstrom vyšší)
    • složitá (rotujeme dvakrát pokaždé v opačném směru)

  • rotace probíhají vždy skrze uzel, jehož koeficient vyváženosti je narušen

  • rotace si můžeme představit jako řetěz, za který zatáhneme a levý/pravý podstrom posuneme

Příklad pravé rotace
obr. 2: Příklad pravé rotace. T označuje podstromy, x a y jsou uzly.
Převzato z: https://akela.mendelu.cz/~foltynek/TI/old/TI13%20Stromy.pdf

Zdroje